偏振片的起偏和检偏 马吕斯定律

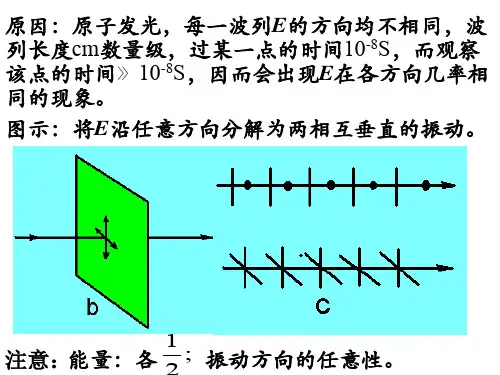
偏振光实验——验证马吕斯定律【原理】光是电磁波，而且是一种横波。

光的电矢量在垂直于传播方向的平面内可以任意取向，若对于传播方向不对称而偏于某个方向称为偏振。

光矢量振动方同与传播方向组成振动面，限于某个固定振动方向的称线偏振光，或从振动面来看，也称为平面偏振光。

此外，还有一种偏振光，它的光矢量末端在垂直于传播方向的平面上随时间变化的轨迹呈椭圆或圆，故称之为椭圆偏振光或圆偏振光。

本实验主要观察线偏振光（平面偏振光）。

偏振器一般指线偏振器，它只允许电矢量沿某一特定方向的线偏振光通过。

普通光源发出的为自然光，经过偏振器后成为线偏振光，这样的偏振器称起振器。

当偏振器用来检验一个光是否偏振光时，则称为检偏器。

用二色性物质制作的偏振片允许特定方向的光振动通过（这一特定方向称该偏振片的透光轴），而吸收与透光轴方向垂直的光振动。

对于理想起偏器，自然光透过它之后应变成完全线偏振光。

当线偏振光再次透过作为理想检偏器的同样的偏振片时，如果检偏器与起偏器透光轴互相平行，则透过的偏振光光强不变。

而当二透光轴相互垂直时，透射光完全不能通过，光强为零。

一般情况下，二平行放置的偏振片的透光轴互成θ角，设入射到第二片偏振片的偏振光振动振幅为E 0，光强I 0，则从第二片偏振片透射出来的偏振光振动振幅变为θcos 0E ，光强，称作马吕斯定律。

本实验即是对它作验证。

θθ2020cos )cos (I E I ==当然，实际的偏振片都不是理想偏振片，由于材料、制作因素以及不可避免的表面反射、散射等原因，马吕斯定律只是近似成立。

如果实验中器件安置或操作不够良好，还会产生更大差异，是应尽力避免的。

本实验使用光强传感器，光源可选用普通光源或半导体激光光源。

利用计算机辅实时测量设备建立光强——角度)(ϕ−I 、光强——余弦)cos (φ−I 、光强——平方余弦图，进行研究分析，以令人信服的证据验证马吕斯定律。

其中角度的测量，还可以使用旋转移动传感器与偏振片连动，以1440点/转的灵敏度自动记录测量数据。

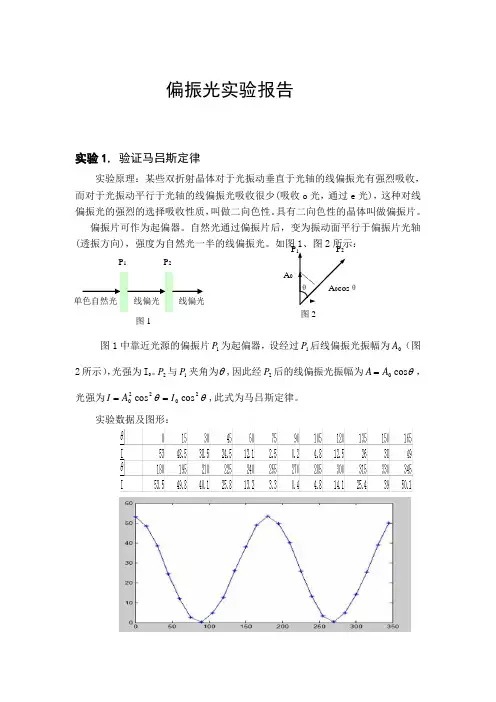
偏振光实验报告实验1. 验证马吕斯定律实验原理：某些双折射晶体对于光振动垂直于光轴的线偏振光有强烈吸收，而对于光振动平行于光轴的线偏振光吸收很少(吸收o 光，通过e 光)，这种对线偏振光的强烈的选择吸收性质，叫做二向色性。

具有二向色性的晶体叫做偏振片。

偏振片可作为起偏器。

自然光通过偏振片后，变为振动面平行于偏振片光轴(透振方向)，强度为自然光一半的线偏振光。

如图1、图2所示：图1中靠近光源的偏振片1P 为起偏器，设经过1P 后线偏振光振幅为0A （图2所示），光强为I 0。

2P 与1P 夹角为θ,因此经2P 后的线偏振光振幅为θcos 0A A =，光强为θθ20220cos cos I A I ==,此式为马吕斯定律。

实验数据及图形：P 1 P 2 线偏光 单色自然光线偏光 图1 P 1 P 2A 0 A 0cos θ θ 图2从图形中可以看出符合余弦定理，数据正确。

实验2.半波片，1/4波片作用实验原理：偏振光垂直通过波片以后，按其振动方向（或振动面）分解为寻常光（o 光）和非常光（e 光）。

它们具有相同的振动频率和固定的相位差（同波晶片的厚度成正比），若将它们投影到同一方向，就能满足相干条件，实现偏振光的干涉。

分振动面的干涉装置如图3所示，M 和N 是两个偏振片，C 是波片，单色自然光通过M 变成线偏振光，线偏振光在波片C 中分解为o 光和e 光，最后投影在N 上，形成干涉。

考虑特殊情况，当M ⊥N 时，即两个偏振片的透振方向垂直时，出射光强为：)cos 1)(2(sin 420δθ-=⊥I I ；当M ∥N 时，即两个偏振片的透振方向平行时，出射光强为：)cos cos sin 2cos sin 21(222220//δθθθθ+-=I I 。

其中θ为波片光轴与M 透振方向的夹角，δ为o 光和e 光的总相位差（同波晶片的厚度成正比）。

改变θ、δ中的任何一个都可以改变屏幕上的光强。

当δ=（2k+1）π（1/2波片）时，cos δ=-1，θ22sin 20I I =⊥，出射光强最大，2)21(sin 20//θ-=I I ，出射光强最小；当δ=[（2k+1）π]/2（1/4波片）时，cos δ=0，)2(sin 420θI I =⊥,)2sin 2(420//θ-=I I 。

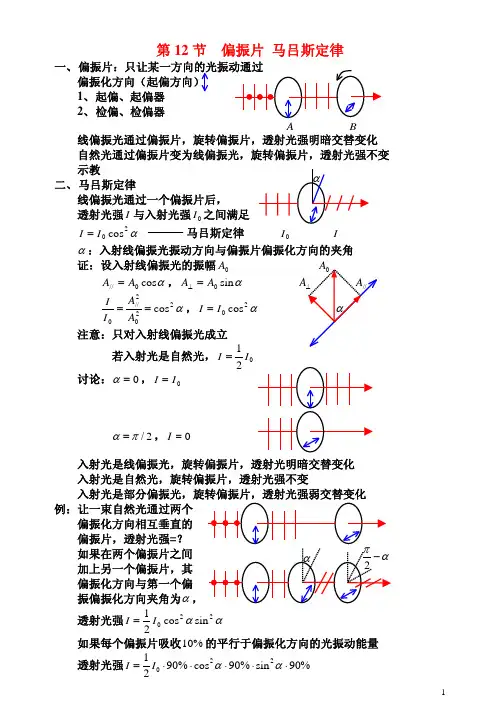
第12节 偏振片 马吕斯定律一、 偏偏振化方向（起偏方向）1、 起偏、起偏器2、 检偏、检偏器A B 线偏振光通过偏振片，旋转偏振片，透射光强明暗交替变化 自然光通过偏振片变为线偏振光，旋转偏振片，透射光强不变 示教二、 马吕斯定律 线偏振光通过一个偏振片后，透射光强I 与入射光强之间满足0I α20cos I I = 马吕斯定律α证：设入射线偏振光的振幅 0A αcos 0//A A =，αsin 0A A =⊥ α2202//0cos ==A A I I，α20cos I I = 注意：只对入射线偏振光成立若入射光是自然光，01I I = 讨论：0=α，0I I =2/πα=，0=I例：让一束自然光通过两个偏振化方向相互垂直的偏振片，透射光强=？如果在两个偏振片之间 加上另一个偏振片，其 偏振化方向与第一个偏振偏振化方向夹角为α，透射光强αα220sin cos 21I I =如果每个偏振片吸收的平行于偏振化方向的光振动能量 %10透射光强%90sin %90cos %9021220⋅⋅⋅⋅⋅=ααI I第13节 反射和折射光的偏振入射面：（入射线，法线）Π反射定律i i =′折射定律γsin sin 21n i n = M ′反射光和折射光都是部分偏振光 反射光中，⊥振动多于//振动折射光中，//振动多于振动⊥120n n arctg i i ==时 反射光为完全偏振光，只包含⊥0i ：布儒斯特角（起偏角） 120n n tgi =：布儒斯特定律 注意：（1）0i i =时，只反射部分⊥振动，不反射//振动 折射光中包含其余的⊥振动和全部的//振动折射光仍是部分偏振光（2）0i i =时，反射光线⊥折射光线证明：γsin sin 201n i n =，120n n tgi ==00cos sin i i ，0201cos sin i n i n = γsin 2n =，02cos i n γsin ==0cos i )sin(0i −π，20πγ=+i（3）自然光以布儒斯特角 照射玻璃片堆，可使折射光成为完全偏振光折射光中只剩下//振动例：一束自然光以布儒斯特角从空气照射玻璃片，界面2上的反射光是（）自然光A （B ）完全偏振光，光矢量振动方向⊥（）完全偏振光，光矢量振动方向// C （）部分偏振光D 解：对界面1，是布儒斯特角，对界面2，0i γ是布儒斯特角 120n n tgi =，20πγ=+i ，210n n ctgi tg ==γ 例：第14节 晶体的双折射现象一、晶体的双折射现象用自然光照射某些晶体（方解石）表面 产生两条折射光线 双折射现象，示教特点：（1） 寻常光线（o 光），遵守折射定律非常光线（e 光），不遵守折射定律（2） 两条光线都是线偏振光，振向不同（3） 光轴（光线沿该方向入射不产生双折射）p253，单轴晶体，双轴晶体某条光线与光轴构成的平面：该光线的主平面 （光，光轴）：o 光主平面 Πo （光，光轴）：e 光主平面Πe （4）光振向o ⊥o 光主平面光振向//光主平面e e 二、 对双折射的解释产生双折射的原因： o 光、光在晶体中的传播速度不同e o 光波面是球面，光波面是旋转椭球面e 沿光轴方向o 光、e 光速度相同垂直光轴方向o 光、e 光速度相差最大o V ：e 光速度oo V e Vo V e e o 晶体对光的折射率，o o n V c =/o e e n V c =/晶体对e 光的折射率 、：晶体的主折射率o n e n 1、 平行光斜入射（光轴位于 2、平行光垂直入射（光轴位于 入射面内，光轴与界面斜交） 入射面内，光轴与界面斜交）3、 平行光垂直入射（光轴平行4、平行光垂直入射（光轴位于 界面，光轴位于入射面内） 入射面内，光轴垂直界面）光轴光同传播方向，但速度不同 光同传播方向，速度相同 e o ,e o , 仍属于双折射 不属于双折射5、 平行光斜入射（光轴//界面，光轴垂直入射面）光、光都遵守折射定律，o e e e o o n n i n γγsin sin sin 1==三、 偏振棱镜1、 尼科耳（棱镜）用加拿大树胶粘在一起加拿大树胶对o 2、 渥拉斯顿镜两块方解石直角棱镜构成两者光轴相垂直负晶体，，e e V >o V e n n <垂直板面振动的光线： 对第一块棱镜是o 光对第二块棱镜是e 光平行板面振动的光线： 对第一块棱镜是e 光对第二块棱镜是o 光垂直板面振动的光线由o 光，光密→光疏，折射光偏离法线 →e 平行板面振动的光线由e 光，光疏→光密，折射光靠近法线 →o 两条光线分开，都是线偏振光四、 偏振片某些双折射晶体对o 光和e获得偏振光的方法：（1）偏振片（2）偏振棱镜（3）以布儒斯特角照射玻璃片例：两块偏振片叠放在一起，其偏振化方向夹角，用强度相同的o 30自然光和线偏振光混合而成的光束垂直入射，已知两成分的入 射光透射后强度相等求：（1）入射光中线偏振光振向与第一块偏振片偏振化方向夹角（2）透射光强与入射光强之比（3）若每个偏振片对透射光吸收率为，%5 再求透射光强与入射光强之比解：（1）设入射线偏振光强为I ，入射自然光强为Io o 30cos 2130cos cos 222I I =α，21cos 2=α，o45=α （2）375.083230cos 2130cos cos 222==+=I I I oo α入射光强透射光强（3）=入射光强透射光强=I I I 2%9530cos %9521%9530cos %95cos 222⋅⋅+⋅⋅⋅o o α=338.0%)95(832=×。

四、马吕斯定律光是400-760nm 范围内的电磁波，对应着红、橙、黄、绿、青、蓝、紫光等。

光波有两个分振动：电矢量E 和磁矢量H ，它们的振动方向都与光的传播方向垂直，因此光是横波。

在光和物质的相互作用过程中主要起作用的是电矢量E，我们称其为光矢量。

而光矢量的振动对于传播方向又具有不对称性，称为光的偏振。

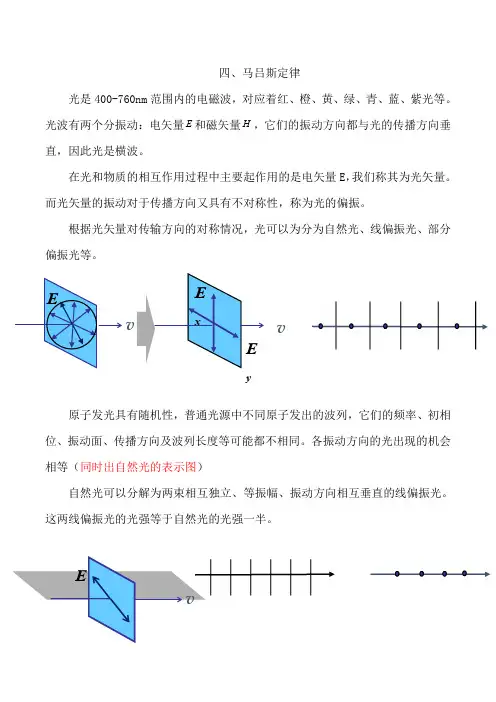
根据光矢量对传输方向的对称情况，光可以为分为自然光、线偏振光、部分偏振光等。

原子发光具有随机性，普通光源中不同原子发出的波列，它们的频率、初相位、振动面、传播方向及波列长度等可能都不相同。

各振动方向的光出现的机会相等（同时出自然光的表示图）自然光可以分解为两束相互独立、等振幅、振动方向相互垂直的线偏振光。

这两线偏振光的光强等于自然光的光强一半。

Ey EE x v vvE如果所有的光矢量都在一个平面内振动，我们称之为线偏振光或者平面偏振光。

如果将自然光中的两个垂直分量中的其中一个分量部分地削弱，所得的光线称为部分偏振光。

E E xv vE y部分偏振光一般光源发的光都是自然光，那如何获得偏振光呢？某些材料对某一方向的光振动全部吸收，允许与之垂直的光振动通过,这种性质称二向色性。

将二向色性物质涂抹到拨片上，则会由自然光获得一束偏振光。

此拨片称为偏振片，透射方向称为偏振片的偏振化方向。

偏振化方向(透振方向）使用偏振片由自然光获得偏振光的过程称为起偏，此偏振片称为起偏器。

使用偏振片检验某束光是否偏振光的过程称为检偏，此偏振片称为检偏器。

在进行检偏过程的时候，光屏上的亮度会随着检偏器的旋转而变化（动画展示）。

那出射光强大小可由马吕斯定律计算出来。

起偏器自然光s I若检偏器与起偏器的偏振化方向是任意角度α，则只有振动方向与检偏器的偏振化方向一致的偏振光可以通过检偏器。

假设二者之间的偏振光振幅为0A ，显然只有和透射轴同向的A 分量可以通过检偏器00cos cos A A A A αα=⇒=已知光的强度和振幅的平方成正比，若强度为0I 的偏振光，通过检偏器厚的强度为I ，则22200cos I A I A α==20cos I I α=这个公式称为马吕斯定律，它表示透过检偏器的光强度与起偏器和检偏器偏振化方向之间（或偏振光的偏振方向与检偏器的偏振化方向之间的）的夹角α有关，并且与该角度余弦的平方成正比。

偏振光干涉实验报告偏振光实验报告实验1. 验证马吕斯定律实验原理：某些双折射晶体对于光振动垂直于光轴的线偏振光有强烈吸收，而对于光振动平行于光轴的线偏振光吸收很少(吸收o光，通过e光)，这种对线偏振光的强烈的选择吸收性质，叫做二向色性。

具有二向色性的晶体叫做偏振片。

偏振片可作为起偏器。

自然光通过偏振片后，变为振动面平行于偏振片光轴(透振方向)，强度为自然光一半的线偏振光。

如图 P1、图2所示：P1 P2 图1 图2 θA 0 图1中靠近光源的偏振片P1为起偏器，设经过P1后线偏振光振幅为A0（图2所示），光强为I0。

P2与P1夹角为?,因此经P2后的线偏振光振幅为A?A0cos?，2光强为I?A0cos2??I0cos2?,此式为马吕斯定律。

实验数据及图形：从图形中可以看出符合余弦定理，数据正确。

实验2.半波片，1/4波片作用实验原理：偏振光垂直通过波片以后，按其振动方向（或振动面）分解为寻常光（o光）和非常光（e光）。

它们具有相同的振动频率和固定的相位差（同波晶片的厚度成正比），若将它们投影到同一方向，就能满足相干条件，实现偏振光的干涉。

分振动面的干涉装置如图3所示，M和N是两个偏振片，C是波片，单色自然光通过M变成线偏振光，线偏振光在波片C中分解为o光和e光，最后投影在N上，形成干涉。

偏振片波片偏振片图3 分振动面干涉装置考虑特殊情况，当M⊥N时，即两个偏振片的透振方向垂直时，出射光强为：I0(sin22?)(1?cos?)；当M∥N时，即两个偏振片的透振方向平行时，出射4I0(1?2sin2?cos2??2sin2?cos2?cos?)。

其中θ为波片光轴与M2I??光强为：I//?透振方向的夹角，δ为o光和e光的总相位差（同波晶片的厚度成正比）。

改变θ、δ中的任何一个都可以改变屏幕上的光强。

当δ=（2k+1）π（1/2波片）时，cosδ=-1，I??强最大，I//?02sin22?，出射光I0(1?sin2?)2，出射光强最小；当δ=[（2k+1）π]/2（1/4波片）时，cosδ=0，I??I0I(sin22?),I//?0(2?sin22?)。

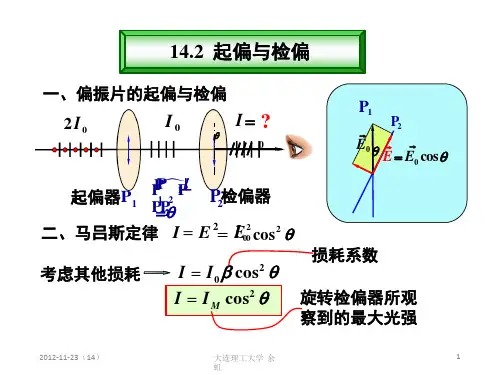
实验： 光偏振与马吕斯定律一．实验目的1.观察光的偏振现象。

2.验证马吕斯定律。

二．实验原理偏振光定义：偏振光是指光矢量的振动方向不变，或具有某种规则地变化的光波。

分类：1.自然光：光矢量具有轴对称性、均匀分布、各方向振动 的振幅相同； 2. 部分偏振光 含有各种振动方向的光矢量，但光振动在某一方向更显著； 3. 完全偏振光：线偏振光：光矢量端点的轨迹为直线； 椭圆偏振光：光矢量端点的轨迹为一椭圆； 圆偏振光：光矢量端点的轨迹为一圆。

马吕斯定律：光强0I 的线偏振光，透过检偏器以后，透射光光强为I=α20cos I ，α是线偏振光的光振动方向与检偏器透振方向间的夹角。

三．实验主要步骤或操作要点实验装置：电脑液晶屏，手机（Phyphox-光强），偏振片（偏光镜，3d 眼镜等），量角器（或者手机Phyphox-斜面）。

实验步骤 ：1.将手机竖直放置在液晶屏前； 2. 打开Phyphox-光模式；3. 将偏光片放置在手机光传感器前；4. 旋转特定角度，记录光强变化和角度（第二个手机Phyphox-斜面 测量角度)；5. 处理数据。

注意事项：角度要准确测量；背景光的影响；测量光路要等高同轴。

实验安全：禁用大功率激光笔 ！实验中禁止将激光聚焦 ！ 做好激光防护，既要保护自己，也要避免误伤他 人 ！ 严禁用眼睛直视激光束，以免造成视网膜损伤。

四．实验数据在0-180 范围内取不同的α（实际上0-90也可以进行验证，但是为了防止偏振片薄厚不均和对光源的反射率不同，采用0-180进行验证），计算α2cos 并记下对应的光强I 。

量角器的分度值为1。

五．数据处理在上述表格基础上计算α2cos ，绘制I-α2cos 图像，并计算I 与α2cos 的线性相关系数。

用Excel 作图像如下：由I-α2cos 图像可知，I 与α2cos 近似成线性关系，斜率0I =1471.1lux ，相关系数R 2=0.9995，线性相关指数接近1。