马吕斯定律
- 格式:doc
- 大小:490.23 KB
- 文档页数:6

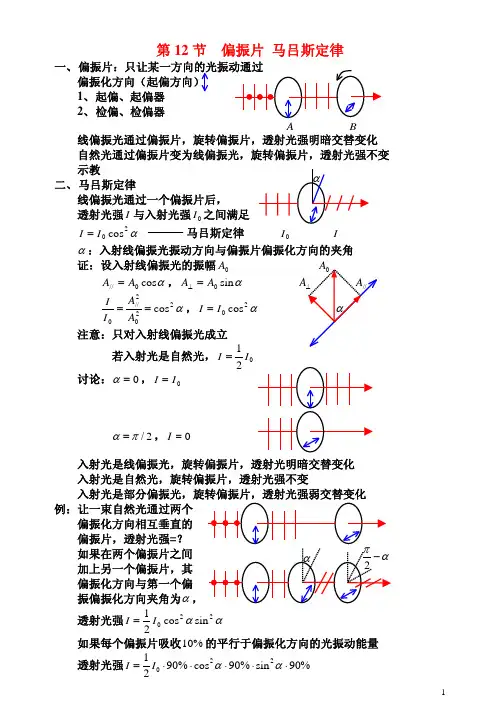
第12节 偏振片 马吕斯定律一、 偏偏振化方向(起偏方向)1、 起偏、起偏器2、 检偏、检偏器A B 线偏振光通过偏振片,旋转偏振片,透射光强明暗交替变化 自然光通过偏振片变为线偏振光,旋转偏振片,透射光强不变 示教二、 马吕斯定律 线偏振光通过一个偏振片后,透射光强I 与入射光强之间满足0I α20cos I I = 马吕斯定律α证:设入射线偏振光的振幅 0A αcos 0//A A =,αsin 0A A =⊥ α2202//0cos ==A A I I,α20cos I I = 注意:只对入射线偏振光成立若入射光是自然光,01I I = 讨论:0=α,0I I =2/πα=,0=I例:让一束自然光通过两个偏振化方向相互垂直的偏振片,透射光强=?如果在两个偏振片之间 加上另一个偏振片,其 偏振化方向与第一个偏振偏振化方向夹角为α,透射光强αα220sin cos 21I I =如果每个偏振片吸收的平行于偏振化方向的光振动能量 %10透射光强%90sin %90cos %9021220⋅⋅⋅⋅⋅=ααI I第13节 反射和折射光的偏振入射面:(入射线,法线)Π反射定律i i =′折射定律γsin sin 21n i n = M ′反射光和折射光都是部分偏振光 反射光中,⊥振动多于//振动折射光中,//振动多于振动⊥120n n arctg i i ==时 反射光为完全偏振光,只包含⊥0i :布儒斯特角(起偏角) 120n n tgi =:布儒斯特定律 注意:(1)0i i =时,只反射部分⊥振动,不反射//振动 折射光中包含其余的⊥振动和全部的//振动折射光仍是部分偏振光(2)0i i =时,反射光线⊥折射光线证明:γsin sin 201n i n =,120n n tgi ==00cos sin i i ,0201cos sin i n i n = γsin 2n =,02cos i n γsin ==0cos i )sin(0i −π,20πγ=+i(3)自然光以布儒斯特角 照射玻璃片堆,可使折射光成为完全偏振光折射光中只剩下//振动例:一束自然光以布儒斯特角从空气照射玻璃片,界面2上的反射光是()自然光A (B )完全偏振光,光矢量振动方向⊥()完全偏振光,光矢量振动方向// C ()部分偏振光D 解:对界面1,是布儒斯特角,对界面2,0i γ是布儒斯特角 120n n tgi =,20πγ=+i ,210n n ctgi tg ==γ 例:第14节 晶体的双折射现象一、晶体的双折射现象用自然光照射某些晶体(方解石)表面 产生两条折射光线 双折射现象,示教特点:(1) 寻常光线(o 光),遵守折射定律非常光线(e 光),不遵守折射定律(2) 两条光线都是线偏振光,振向不同(3) 光轴(光线沿该方向入射不产生双折射)p253,单轴晶体,双轴晶体某条光线与光轴构成的平面:该光线的主平面 (光,光轴):o 光主平面 Πo (光,光轴):e 光主平面Πe (4)光振向o ⊥o 光主平面光振向//光主平面e e 二、 对双折射的解释产生双折射的原因: o 光、光在晶体中的传播速度不同e o 光波面是球面,光波面是旋转椭球面e 沿光轴方向o 光、e 光速度相同垂直光轴方向o 光、e 光速度相差最大o V :e 光速度oo V e Vo V e e o 晶体对光的折射率,o o n V c =/o e e n V c =/晶体对e 光的折射率 、:晶体的主折射率o n e n 1、 平行光斜入射(光轴位于 2、平行光垂直入射(光轴位于 入射面内,光轴与界面斜交) 入射面内,光轴与界面斜交)3、 平行光垂直入射(光轴平行4、平行光垂直入射(光轴位于 界面,光轴位于入射面内) 入射面内,光轴垂直界面)光轴光同传播方向,但速度不同 光同传播方向,速度相同 e o ,e o , 仍属于双折射 不属于双折射5、 平行光斜入射(光轴//界面,光轴垂直入射面)光、光都遵守折射定律,o e e e o o n n i n γγsin sin sin 1==三、 偏振棱镜1、 尼科耳(棱镜)用加拿大树胶粘在一起加拿大树胶对o 2、 渥拉斯顿镜两块方解石直角棱镜构成两者光轴相垂直负晶体,,e e V >o V e n n <垂直板面振动的光线: 对第一块棱镜是o 光对第二块棱镜是e 光平行板面振动的光线: 对第一块棱镜是e 光对第二块棱镜是o 光垂直板面振动的光线由o 光,光密→光疏,折射光偏离法线 →e 平行板面振动的光线由e 光,光疏→光密,折射光靠近法线 →o 两条光线分开,都是线偏振光四、 偏振片某些双折射晶体对o 光和e获得偏振光的方法:(1)偏振片(2)偏振棱镜(3)以布儒斯特角照射玻璃片例:两块偏振片叠放在一起,其偏振化方向夹角,用强度相同的o 30自然光和线偏振光混合而成的光束垂直入射,已知两成分的入 射光透射后强度相等求:(1)入射光中线偏振光振向与第一块偏振片偏振化方向夹角(2)透射光强与入射光强之比(3)若每个偏振片对透射光吸收率为,%5 再求透射光强与入射光强之比解:(1)设入射线偏振光强为I ,入射自然光强为Io o 30cos 2130cos cos 222I I =α,21cos 2=α,o45=α (2)375.083230cos 2130cos cos 222==+=I I I oo α入射光强透射光强(3)=入射光强透射光强=I I I 2%9530cos %9521%9530cos %95cos 222⋅⋅+⋅⋅⋅o o α=338.0%)95(832=×。

四、马吕斯定律光是400-760nm 范围内的电磁波,对应着红、橙、黄、绿、青、蓝、紫光等。
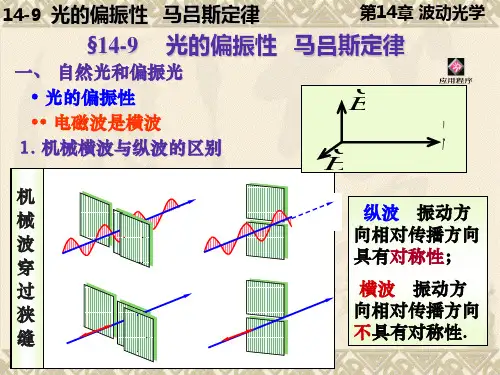
光波有两个分振动:电矢量E 和磁矢量H ,它们的振动方向都与光的传播方向垂直,因此光是横波。
在光和物质的相互作用过程中主要起作用的是电矢量E,我们称其为光矢量。
而光矢量的振动对于传播方向又具有不对称性,称为光的偏振。
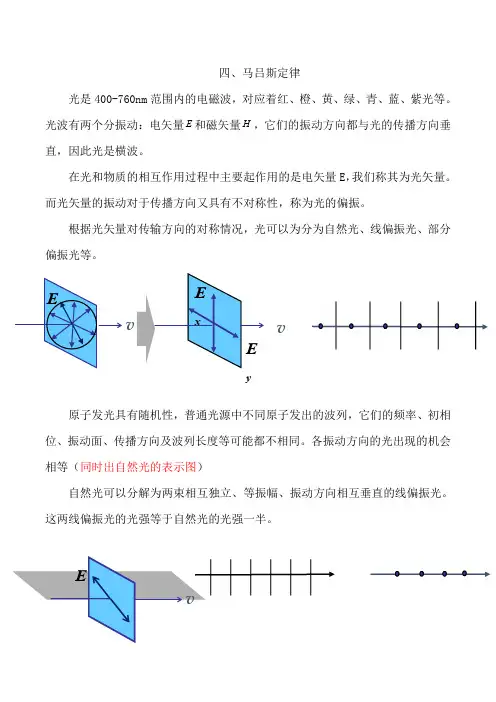
根据光矢量对传输方向的对称情况,光可以为分为自然光、线偏振光、部分偏振光等。
原子发光具有随机性,普通光源中不同原子发出的波列,它们的频率、初相位、振动面、传播方向及波列长度等可能都不相同。
各振动方向的光出现的机会相等(同时出自然光的表示图)自然光可以分解为两束相互独立、等振幅、振动方向相互垂直的线偏振光。
这两线偏振光的光强等于自然光的光强一半。
Ey EE x v vvE如果所有的光矢量都在一个平面内振动,我们称之为线偏振光或者平面偏振光。
如果将自然光中的两个垂直分量中的其中一个分量部分地削弱,所得的光线称为部分偏振光。
E E xv vE y部分偏振光一般光源发的光都是自然光,那如何获得偏振光呢?某些材料对某一方向的光振动全部吸收,允许与之垂直的光振动通过,这种性质称二向色性。
将二向色性物质涂抹到拨片上,则会由自然光获得一束偏振光。
此拨片称为偏振片,透射方向称为偏振片的偏振化方向。
偏振化方向(透振方向)使用偏振片由自然光获得偏振光的过程称为起偏,此偏振片称为起偏器。
使用偏振片检验某束光是否偏振光的过程称为检偏,此偏振片称为检偏器。
在进行检偏过程的时候,光屏上的亮度会随着检偏器的旋转而变化(动画展示)。
那出射光强大小可由马吕斯定律计算出来。
起偏器自然光s I若检偏器与起偏器的偏振化方向是任意角度α,则只有振动方向与检偏器的偏振化方向一致的偏振光可以通过检偏器。
假设二者之间的偏振光振幅为0A ,显然只有和透射轴同向的A 分量可以通过检偏器00cos cos A A A A αα=⇒=已知光的强度和振幅的平方成正比,若强度为0I 的偏振光,通过检偏器厚的强度为I ,则22200cos I A I A α==20cos I I α=这个公式称为马吕斯定律,它表示透过检偏器的光强度与起偏器和检偏器偏振化方向之间(或偏振光的偏振方向与检偏器的偏振化方向之间的)的夹角α有关,并且与该角度余弦的平方成正比。

马吕斯定律电阻和电流的平衡分析马吕斯定律是电学中的一个重要定律,描述了电阻和电流之间的平衡关系。
在电路中,电阻是电流通过的障碍物,而电流则是电荷在电路中的流动。
马吕斯定律通过数学公式和实验结果,揭示了电阻和电流之间的定量关系。
1. 马吕斯定律的表达式马吕斯定律可以用以下数学公式来表示:V = I * R其中,V表示电压(单位为伏特),I表示电流(单位为安培),R表示电阻(单位为欧姆)。
这个公式说明了在一个闭合电路中,电压等于电流乘以电阻。
2. 马吕斯定律的原理马吕斯定律的原理可以通过以下几个方面来解释:2.1 电压的定义在物理学中,电压被定义为单位正电荷所具有的能量。
当一个正电荷从高电压区域移动到低电压区域时,它会释放能量。
这个能量释放过程就是我们常说的电流。
2.2 电阻的作用电阻是电流通过的障碍物,它会阻碍电流的流动。
电阻的大小取决于电路中的材料和几何形状。
当电流通过电阻时,电阻会将电能转化为其他形式的能量,如热能。
2.3 电流的平衡根据马吕斯定律,电压等于电流乘以电阻。
这意味着在一个闭合电路中,当电压和电阻给定时,电流的大小是确定的。
如果电压增大,那么电流也会增大;如果电阻增大,那么电流会减小。
3. 马吕斯定律的应用马吕斯定律在实际应用中有着广泛的应用,以下是一些常见的应用场景:3.1 电路设计在设计电路时,我们需要根据所需的电压和电流来选择合适的电阻。
通过马吕斯定律,我们可以计算出所需的电阻值,从而满足设计要求。
3.2 电子设备在各种电子设备中,马吕斯定律被广泛应用于计算和控制电流。
例如,在手机充电器中,通过控制电压和电阻的关系,可以实现对电池的快速充电。
3.3 电路故障排查当电路出现故障时,我们可以利用马吕斯定律来分析问题所在。
通过测量电压和电流的数值,我们可以判断是否存在电阻异常或者其他故障。
4. 总结马吕斯定律是电学中一个重要的定律,描述了电阻和电流之间的平衡关系。
通过马吕斯定律,我们可以计算和控制电路中的电流,从而满足设计要求。


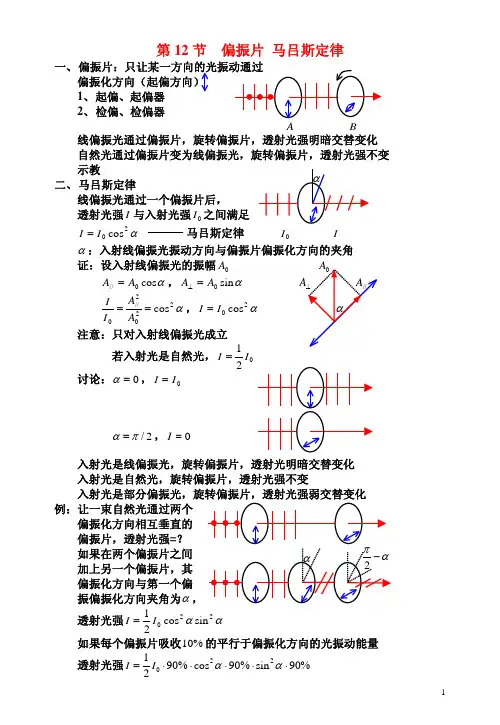
第12节 偏振片 马吕斯定律一、 偏偏振化方向(起偏方向)1、 起偏、起偏器2、 检偏、检偏器A B 线偏振光通过偏振片,旋转偏振片,透射光强明暗交替变化 自然光通过偏振片变为线偏振光,旋转偏振片,透射光强不变 示教二、 马吕斯定律 线偏振光通过一个偏振片后,透射光强I 与入射光强之间满足0I α20cos I I = 马吕斯定律α证:设入射线偏振光的振幅 0A αcos 0//A A =,αsin 0A A =⊥ α2202//0cos ==A A I I,α20cos I I = 注意:只对入射线偏振光成立若入射光是自然光,01I I = 讨论:0=α,0I I =2/πα=,0=I例:让一束自然光通过两个偏振化方向相互垂直的偏振片,透射光强=?如果在两个偏振片之间 加上另一个偏振片,其 偏振化方向与第一个偏振偏振化方向夹角为α,透射光强αα220sin cos 21I I =如果每个偏振片吸收的平行于偏振化方向的光振动能量 %10透射光强%90sin %90cos %9021220⋅⋅⋅⋅⋅=ααI I第13节 反射和折射光的偏振入射面:(入射线,法线)Π反射定律i i =′折射定律γsin sin 21n i n = M ′反射光和折射光都是部分偏振光 反射光中,⊥振动多于//振动折射光中,//振动多于振动⊥120n n arctg i i ==时 反射光为完全偏振光,只包含⊥0i :布儒斯特角(起偏角) 120n n tgi =:布儒斯特定律 注意:(1)0i i =时,只反射部分⊥振动,不反射//振动 折射光中包含其余的⊥振动和全部的//振动折射光仍是部分偏振光(2)0i i =时,反射光线⊥折射光线证明:γsin sin 201n i n =,120n n tgi ==00cos sin i i ,0201cos sin i n i n = γsin 2n =,02cos i n γsin ==0cos i )sin(0i −π,20πγ=+i(3)自然光以布儒斯特角 照射玻璃片堆,可使折射光成为完全偏振光折射光中只剩下//振动例:一束自然光以布儒斯特角从空气照射玻璃片,界面2上的反射光是()自然光A (B )完全偏振光,光矢量振动方向⊥()完全偏振光,光矢量振动方向// C ()部分偏振光D 解:对界面1,是布儒斯特角,对界面2,0i γ是布儒斯特角 120n n tgi =,20πγ=+i ,210n n ctgi tg ==γ 例:第14节 晶体的双折射现象一、晶体的双折射现象用自然光照射某些晶体(方解石)表面 产生两条折射光线 双折射现象,示教特点:(1) 寻常光线(o 光),遵守折射定律非常光线(e 光),不遵守折射定律(2) 两条光线都是线偏振光,振向不同(3) 光轴(光线沿该方向入射不产生双折射)p253,单轴晶体,双轴晶体某条光线与光轴构成的平面:该光线的主平面 (光,光轴):o 光主平面 Πo (光,光轴):e 光主平面Πe (4)光振向o ⊥o 光主平面光振向//光主平面e e 二、 对双折射的解释产生双折射的原因: o 光、光在晶体中的传播速度不同e o 光波面是球面,光波面是旋转椭球面e 沿光轴方向o 光、e 光速度相同垂直光轴方向o 光、e 光速度相差最大o V :e 光速度oo V e Vo V e e o 晶体对光的折射率,o o n V c =/o e e n V c =/晶体对e 光的折射率 、:晶体的主折射率o n e n 1、 平行光斜入射(光轴位于 2、平行光垂直入射(光轴位于 入射面内,光轴与界面斜交) 入射面内,光轴与界面斜交)3、 平行光垂直入射(光轴平行4、平行光垂直入射(光轴位于 界面,光轴位于入射面内) 入射面内,光轴垂直界面)光轴光同传播方向,但速度不同 光同传播方向,速度相同 e o ,e o , 仍属于双折射 不属于双折射5、 平行光斜入射(光轴//界面,光轴垂直入射面)光、光都遵守折射定律,o e e e o o n n i n γγsin sin sin 1==三、 偏振棱镜1、 尼科耳(棱镜)用加拿大树胶粘在一起加拿大树胶对o 2、 渥拉斯顿镜两块方解石直角棱镜构成两者光轴相垂直负晶体,,e e V >o V e n n <垂直板面振动的光线: 对第一块棱镜是o 光对第二块棱镜是e 光平行板面振动的光线: 对第一块棱镜是e 光对第二块棱镜是o 光垂直板面振动的光线由o 光,光密→光疏,折射光偏离法线 →e 平行板面振动的光线由e 光,光疏→光密,折射光靠近法线 →o 两条光线分开,都是线偏振光四、 偏振片某些双折射晶体对o 光和e获得偏振光的方法:(1)偏振片(2)偏振棱镜(3)以布儒斯特角照射玻璃片例:两块偏振片叠放在一起,其偏振化方向夹角,用强度相同的o 30自然光和线偏振光混合而成的光束垂直入射,已知两成分的入 射光透射后强度相等求:(1)入射光中线偏振光振向与第一块偏振片偏振化方向夹角(2)透射光强与入射光强之比(3)若每个偏振片对透射光吸收率为,%5 再求透射光强与入射光强之比解:(1)设入射线偏振光强为I ,入射自然光强为Io o 30cos 2130cos cos 222I I =α,21cos 2=α,o45=α (2)375.083230cos 2130cos cos 222==+=I I I oo α入射光强透射光强(3)=入射光强透射光强=I I I 2%9530cos %9521%9530cos %95cos 222⋅⋅+⋅⋅⋅o o α=338.0%)95(832=×。


马吕斯定律定义
马吕斯定律,也被称为马吕斯定理,是法国物理学家艾蒂安-路易·马吕斯在1808年阐述的一条几何光学的定理。
该定律指出,光线束在各向同性的均匀介质中传播时,始终保持着与波面的正交性,并且入射波面与出射波面对应点之间的光程均为定值。
具体来说,当强度为I(0)的线偏振光透过检偏片后,透射光的强度(不考虑吸收)为I=I(0)cos²θ,其中θ是入射线偏振光的光振动方向和偏振片偏振化方向之间的夹角。
此外,根据马吕斯定理,正交一致性光束,经过无论多少次的反射和折射,始终保持正交一致。
以上内容仅供参考,如需更多信息,建议查阅关于马吕斯定律的资料或咨询物理学家。
s426验证马吕斯定律在数学和物理学领域,定律是描述和解释自然界中一定规律的陈述。
其中,马吕斯定律是指在人口学中,一国的人口增长速度与其平均人口水平成反比。
本文将探讨并验证马吕斯定律的准确性,并对其可能的应用进行拓展。
马吕斯定律最早由法国数学家和社会学家西蒙·马吕斯于1798年提出。
他注意到,尽管人口增长在短期内可能是指数级的,但随着时间的推移,人口增长率逐渐减缓,并最终趋于稳定。
这意味着,当一个国家的人口达到一定水平时,人口增长将趋于平缓,直至停止。
为了验证马吕斯定律,研究人员可以通过分析历史人口数据来比较实际的人口增长趋势和该定律的预测结果。
他们可能会将不同国家或地区的人口数据进行比较,以了解人口增长率与平均人口水平之间的关系。
许多研究已经证实了马吕斯定律的准确性。
例如,研究表明,当一个国家的平均人口水平较低时,人口增长率通常会较高,但随着平均人口水平的提高,人口增长率会逐渐减缓。
这可能是由于资源限制、教育水平的提高、计划生育政策的推行等因素所致。
马吕斯定律的验证具有重要的实际意义。
了解人口增长与平均人口水平之间的关系,可以帮助政府和决策者制定更有效的人口政策。
例如,在人口稀疏的地区,政府可以采取措施鼓励生育,以增加劳动力和促进经济发展。
而在人口密集的地区,政府可能需要引入计划生育政策,以控制人口增长并减轻资源压力。
此外,马吕斯定律的拓展应用也非常广泛。
除了人口学领域,它还可以应用于其他领域,如生态学、经济学和城市规划等。
在生态学中,人口增长与资源利用之间的关系是一个重要的研究领域。
根据马吕斯定律,当资源有限时,人口增长速度将受到限制。
这对于制定可持续发展策略具有重要的借鉴意义。
总之,马吕斯定律是描述人口增长与平均人口水平之间关系的重要定律。
通过验证其准确性并拓展其应用,我们可以更好地理解和管理人口增长对社会、经济和环境的影响。
这有助于制定更科学和可持续的发展策略,以确保未来的可持续发展。
写出马吕斯定律数学表达式马吕斯定律是热力学中最重要的定律,它说明了热力学变化之间的关系。
它包括物理工程和热力学系统都感兴趣的三大模块:热量、动能和内能。
马吕斯定律表达式如下:q+Δu+Δe=0其中,q表示热量流入系统的量;Δu表示系统的动能的变化;Δe表示系统的内能的变化。
马吕斯定律指出,在任何物理变化过程中,系统的总热流量(q)+系统内总动能变化量(Δu)+系统内的总内能变化量(Δe) 总是为0,即q+ Δu + Δe =0。
马吕斯定律提供了一种理解和分析热力学系统能量变化的重要结构性模型,是这一领域的重要定律。
它为热力学中物理变化的本质提供了可靠的理论基础,为分析和计算热力学系统的输出能量提供了重要工具,也正是这一定律的基础,热力学的深入研究得以实现。
马吕斯定律的表达式为q+Δu+Δe=0,它给出了物理系统热力学能量变化的重要定律,即热量、动能和内能之和是一定的。
它把热能分解为动能和内能,然后在认识和分析热力学系统能量变化规律上发挥着重要作用,给热力学系统的研究带来了重要的量化工具。
马吕斯定律因其重要性受到物理、化学和工程学等多种科学领域的重视,它的基础是利用动量守恒定律和能量守恒定律,能量守恒定律来得出的。
在热力学分析领域中,马吕斯定律为不同的系统提供了可靠的数学模型,可以将计算中的模糊不确定性归结为科学的合理可靠的结论,为热力学的研究和运用带来重要的参考价值。
马斯洛斯定律的重要性不言而喻,它是热力学分析的一个基础,提供了一种客观可靠的描述系统能量变化的有效模型,更加明确了热力学能量流动的规律,使得热力学系统能够处理较精确的变量计算。
它通过把热量分解为动能和内能,有效地对物理系统的物理变化进行了量化地分析,为研究热力学系统的输出能量带来了重要的参考价值。
总的来说,马斯洛斯定律的表达式为q+Δu+Δe=0,它是热力学中最重要的定律,能够准确地计算物理系统能量变化,为热力学分析和套用带来了重要的参考价值,物理、化学和工程领域都对这一定律有着重要的研究价值。
马吕斯定律公式马吕斯定律公式____________________________马吕斯定律公式是一个物理学定律,用来描述物体在重力场中的运动,该定律由哥本哈根的物理学家和天文学家Ole Römer发现。
他在1676年发现,光的速度是一个常数,可以用来计算物体在重力场中的运动。
Ole Römer被称为现代物理学之父,他研究宇宙物理学,在观察到太阳系中行星的运行速度时,他发现它们的运行速度与光速相关。
他认为,由于光的速度是一个常数,因此可以用来描述物体在重力场中的运动。
因此,他提出了一个公式,也就是所谓的“马吕斯定律”。
马吕斯定律公式表明,当一个物体受到重力的影响时,它的运动轨迹将按照一定的函数变化,即:$$F = \frac{mv^2}{r}$$其中,F代表重力力,m代表物体的质量,v代表物体的速度,r代表物体与重力源之间的距离。
根据该公式,重力力F是一个正比于物体质量m和它与重力源之间距离r的倒数的函数,而且正比于物体速度v的平方。
马吕斯定律公式广泛用于物理学、航天学和天文学中。
它被广泛用于研究太阳系内行星、卫星和其他天体的运动轨迹。
例如,由于马吕斯定律公式可以用来描述太阳系内行星的运动轨迹,所以它也被用于航天学中,用于计算航天器飞行时的轨道。
此外,马吕斯定律公式也被用于天文学中。
例如,可以用来研究太阳系内各行星之间的引力相互作用,以及其他天体如星系和星团之间的引力相互作用。
此外,马吕斯定律公式也可以用于研究太阳系内各行星之间的重力场分布情况。
因此,马吕斯定律公式是一个重要的物理学定律,在物理学、航天学和天文学中都有广泛的应用。
该定律可以帮助人们更好地理解太阳系内各行星、卫星和其他天体之间的引力相互作用,以及重力场分布情况,为人们深入研究宇宙提供了重要依据。
马吕斯定律是由美国物理学家威廉·马吕斯于1881年提出的定律,也被称为马吕斯-
马斯卡定律。
它表明,在任何情况下,在一定的温度和压力下,每种物质的分子都有相同的能量。
它的定义是,在同一温度下,每立方厘米的不同气体的分子所能够拥有的能量是
相同的。
它的物理意义是:在一定的温度和压力下,每种物质的分子能量都是相同的,无论它
的分子的结构和大小如何,也无论它的分子的温度和压力如何。
马吕斯定律的重要性在于,它提供了一个可以确定物质性质的基本原理,可以用来研究物质的性质,并用来设计其他实验。
此外,马吕斯定律也为热力学提供了一个基本的原理,可以用来研究能量的变化。
它
的发现也提供了对热力学的理解,使得热力学可以更容易地被描述和理解。
总之,马吕斯定律是一个非常重要的定律,它可以提供一个可以确定物质性质的基本
原理,可以用来研究物质的性质,以及热力学的基本原理。
它的发现也使得热力学可以更
容易地被描述和理解,为物理学和化学的发展做出了重要贡献。
马吕斯定律定义马吕斯定律,又称为任务时间定律,是一种描述人类在完成任务过程中所遵循的普遍规律。
根据马吕斯定律,一个任务所需的时间总是会随着可用时间的增加而填满。
这意味着,无论我们给予一个任务多少时间,我们都会将其充分利用,直到完成为止。
马吕斯定律在我们的日常生活中随处可见。
无论是完成学业、工作任务,还是处理家务、锻炼身体,我们总是会将我们可用的时间充分运用起来,以完成我们所设定的目标。
这种现象背后的原因是人类天性中的一种效率倾向。
当我们有足够的时间去完成一个任务时,我们会倾向于将更多的任务添加到我们的计划中,或者将任务的细节和复杂度增加,以充分利用我们的时间。
这种效率倾向使得我们的任务总是会填满我们可用的时间,使我们感到时间不够用。
马吕斯定律也揭示了我们在时间管理方面的一个困境。
我们往往高估自己的时间管理能力,认为自己可以在有限的时间内完成更多的任务。
然而,实际情况往往是,我们在任务的分配和执行上存在一定的偏差,导致任务的完成时间超出我们最初的预期。
为了应对马吕斯定律的影响,我们需要采取一些有效的时间管理策略。
首先,我们需要明确自己的目标和优先级,将任务分解成具体的步骤,并为每个步骤设定合理的时间限制。
其次,我们需要学会拒绝一些不必要的任务和干扰,以保证我们有足够的时间来专注于重要的任务。
此外,我们还可以利用时间管理工具和技巧,如番茄工作法、时间表和提醒等,来提高我们的工作效率。
马吕斯定律的存在是不可否认的,它揭示了人类在任务完成过程中的一种普遍规律。
了解和应对这一定律,将有助于我们更好地管理我们的时间,提高工作效率,实现我们的目标。
通过合理规划和有效执行,我们可以更好地应对时间的挑战,让我们的生活更加充实和有意义。
院-系:理学院物理系
专业:物理学
年级: 09物理
学生姓名:黄青中
学号: 200902050238
摘要:普遍光源如太阳、白炽灯、钠灯等发光时,组成光源的原子自发或受激辐射光波列是随机的,各光波列振动方向、频率和位相不尽相同,光矢量在垂直于光传播方向的平面上取各方向的几率相等,自然光可分解为两互相垂直方向、振幅相等、没有任何相位关系的偏振光。
若光波中虽包含各种方向的振动,但在某特定方向上的振动占优势,例如在某一方向上的振幅最大,而在与之垂直的另一方向上的振幅最小,则这种偏振光称为部分偏振光。
其优势越大,其偏振化程度越高。
因此,可以用一定方法将自然光变成部份偏振光和偏振光。
关键词:线偏振光、圆偏振光、椭圆偏振光、马吕斯、折射率、
正文:1.光的偏振性(Polarization)
电磁波是横波,光是电磁波在人眼视觉范围内的波段0.4nm 0.7nm。
对应红、橙、黄、绿、青、蓝、紫光。
研究光的振动方向的特性即研究光的偏振性。
光矢量的振动对于传播方向的不对称性,称为为光的偏振。
2. 光偏振态的分类和图示
根据光矢量对传播方向的对称情况,光可以分为:自然光、线偏振光、部分偏振光,以及椭圆偏振光。
线偏振光
光矢量只沿某一固定方向振动的光为线偏振光。
偏振光的振动方向与传播方向组成的平面称为振动面。
线偏振光的振动面是固定不动的。
线偏振光的表示方
法如下:
椭圆偏振光
光矢量末点的运动轨迹是正椭圆或斜椭圆。
在迎光矢量图上,光矢量端点沿逆时针方向旋转的称为左旋偏振光;沿顺时针方向旋转的称为右旋偏振光。
若光波中虽包含各种方向的振动,但在某特定方向上的振动占优势,例如在某一方向上的振幅最大,而在与之垂直的另一方向上的振幅最小,则这种偏振光称为部分偏振光。
其优势越大,其偏振化程度越高。
因此,可以用一定方法将自
然光变成部份偏振光和偏振光。
部分偏振光的两个相互垂直的光振动也没有任何固定的相位关系。
偏振片
两向色性的有机晶体,如硫酸碘奎宁、电气石或聚乙烯醇薄膜在碘溶液中浸
泡后,在高温下拉伸、烘干,然后粘在两
个玻璃片之间就形成了偏振片。
它有一个
特定的方向,只让平行与该方向的振动通
过,这一方向称为透振方向。
1. 起偏
当自然光通过偏振片时,某一方向上的光矢量被吸收,只有另一方向的光矢量透过,从而使自然光成为偏振光,称为起偏。
从起偏器透出的线偏振光的光强是入射自然光的光强的1/2。
2. 检偏
在光路上放一块相同的偏振片,当旋转这一偏振片时,在片后观察,若透射的光强不发生变化,则入射光为自然光,若光强发生变化,则可确定入射光为偏振光,因此该偏振片可进行检偏。
(1)线偏振光
检偏器旋转一周,光强两强两黑。
(2)自然光
在光路中插入检偏器,屏上光强减半。
检偏器旋转,屏上亮暗无变化。
(3)部分偏振光
检偏器旋转一周,屏上光强经历两强两弱变化。
(4)圆偏振光
光矢量端点在垂直于光传播方向的截面内描绘出圆形轨迹。
检偏器旋转一周,光强无变化。
(5)椭圆偏振光
光矢量端点在垂直于光传播方向的截面内描绘出椭圆轨迹。
检偏器旋转一周,光强两强两弱。
1、马吕斯定律
一束光振幅为A
0、光强为I
的线偏光,透过检偏器以后,透射光强为I。
设
α为线偏光的光振动方向OM与检偏器透振方向ON 间的夹角,则可以将入射到检偏器的光振动分解为平行于和垂直于ON 的两个分量,如下图所示。
垂直于ON 的分量不能通过检偏器,只有平行于ON 的分量才能通过检偏器。
因光强正比于光振动的振幅,所以从检偏器透射出来的光强为:
α2
0cos I I =,
α为线偏振光的光振动方向OM 与检偏器透振方向ON 间的夹角。
这就是马吕斯
定律:
αcos 0A A =,2
2
0A A I I =
当=0°或180°时,,透射光最强。
当=90°或270°时,I=0,透射光强为零。
当为其它值时,光强介于 0 和
之间。
一束光强为0I 的自然光透
过检偏器,透射光强为2
/0I 。
2,自准直法测棱镜角
将三棱镜按标识要求放置在载物平台目测粗调使望远镜聚焦于无穷远使望远镜光轴垂直于分光计主轴,望远镜对准AB 面时应调整α2和望远镜倾斜度螺钉望远镜对准AC 面时应调整α1和望远镜倾斜度螺钉使平行光管的光轴垂直于分光计主轴;注意:自准法测α,此要求可以不调,反射法测α,则应在用自准法测得α后从平台上取下三棱镜进行调整;调整完成再按反射法测量要求把三棱镜放置在载物平台上。
计算公式: ф=1/2(ф′+ф″) ф′=| T2′-T1′| 或 ф′=360°-| T2′-T1′| ф″=| T2″-T1″| 或 ф″=360°-| T2″-T1″| 则α=180°-ф
实验数据及处理:1,棱镜顶角的测定 1 2 3
4 5 平均值
1v
31311︒ 32311︒ 34311︒ 36311︒ 32311︒
33311︒
'1v
32131︒ 33313︒
32313︒ 34313︒
33313︒
32313︒
2v
3271︒
3271︒
3371︒
3271︒
3471︒
3271︒
'2v
32251︒
31251︒
32251︒ 34251︒
251︒
32251︒
不确定度的计算:
⋅
=0223
.0)(1v v a ⋅=577.0)(v v b ⋅=619.0)(1v v c '1=a v
顶角的测定:)(2
12'
2
1.1v v v v -+-=θ 最终'160180︒︒=-=θA
计算结果:''1160±=︒A
掠入射法测棱镜折射率: 1 2 3 4 5
平均值
1v
'6335︒
'5335︒
'6335︒ '5335︒
'6335︒
'6335︒
2v
'7155︒
'5155︒
'5155︒
'7155︒ '7155︒ '6155︒
'1v
'4325︒
'4325︒
'6325︒
'6325︒
'6325︒
'5325︒ '2v
'5195︒ '7195︒
'5195︒ '5195︒ '7195︒
'6195︒
计算:
)(2
12'
21'1v v v v i m ---=
'5939︒=m i 2)sin sin cos (1A
i A n m ++=
654.1=n
不确定度的计算:'
1202.0)(=i u a ''577.03
1)(==m b i u
'619.0)(=n c i u 023.0=n u
所以:
023.0654.1±=n
讨论:根据误差分析用掠入射法测出的数据更接近理论值。
参考文献:《普通基础物理实验》杨述武 《光学仪器》 王艳阳。