保守力与非保守力及势能

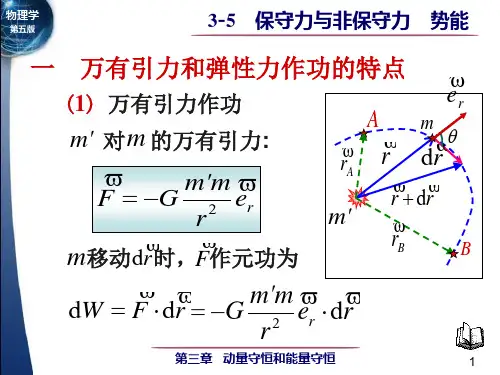
保守力做功公式(一)保守力做功公式在物理学中, 保守力做功公式是一个重要的概念。

保守力是指做功与路径无关的力，而做功则是力对物体做的功。

在这篇文章中，将介绍保守力做功公式以及一些相关的公式，并通过举例进行解释说明。

保守力和非保守力•保守力：保守力是指在特定路径下，力所做的功与路径无关。

它只与起点和终点的位置有关。

例如，重力和弹簧力都是保守力。

保守力与势能（potential energy）密切相关。

•非保守力：非保守力是指在特定路径下，力所做的功与路径有关。

摩擦力和空气阻力都是非保守力。

非保守力导致系统的机械能发生改变。

保守力做功公式保守力做功公式可以表示为：W=−ΔU其中： - W表示力所做的功； -ΔU表示势能的变化。

根据这个公式，如果势能增加，力所做的功为负；如果势能减少，力所做的功为正。

示例示例 1：重力做功考虑一个物体沿直线向上抛掷并上升到最高点。

在上升过程中，重力对物体做的功为负。

我们可以使用保守力做功公式来计算。

假设物体的质量为m，上升的高度为h，重力加速度为g。

在最高点，物体的势能为0。

因此，势能的变化为ΔU=−mgℎ其中h为负值。

根据保守力做功公式，重力对物体做的功为W=−(−mgℎ)=mgℎ可以看到，重力对物体做的功为正，这也符合我们的直觉。

物体上升时，重力做正功，输给了物体。

示例 2：弹簧力做功考虑一个弹簧振子，当振子从一个最大幅度位置经过过盪点后，达到另一个最大幅度位置。

在振子的运动过程中，弹簧力对振子做的功既正也负。

假设振子相对过盪点的位移为x，弹簧的劲度系数为k。

在过盪点，势能为0。

因此，势能的变化为ΔU=−12kx2根据保守力做功公式，弹簧力对振子做的功为W=−(−12kx2)=12kx2可以看到，当振子从最大幅度位置向过盪点运动时，弹簧力对振子做的功为正；当振子从过盪点向最大幅度位置运动时，弹簧力对振子做的功为负。

这也符合我们对弹簧振子运动过程的直观理解。

总结在这篇文章中，我们介绍了保守力做功公式以及与之相关的概念。

浅议物理学中的保守力和势能【摘要】保守力和势能在物理学中扮演着重要的角色。

保守力是指不依赖路径的力，其所做的功与路径无关。

势能则是对保守力的一种描述，是可用于确定力学系统状态的函数。

保守力和势能之间存在着密切的关系，一般通过势能函数来确定。

根据保守力和势能的关系，我们可以推导出机械能守恒定律，即在只受保守力的情况下，力学系统的机械能保持不变。

保守力和非保守力的区别在于是否可以用势能来描述。

保守力和势能的重要性体现在它们对力学系统的描述和分析中起到了关键作用，而在物理学中也有着广泛的应用。

为了更深入地理解和探索保守力和势能，未来的研究方向可能会集中在更复杂系统下的运用和拓展。

【关键词】保守力、势能、物理学、性质、关系、确定、守恒定律、区别、重要性、应用、未来研究方向。

1. 引言1.1 保守力的基本概念保守力是物理学中一个非常重要的概念，它在描述物体运动和相互作用过程中起着至关重要的作用。

保守力是一种在物体运动中所做的功与路径无关的力，即对于沿着任意闭合路径作功的保守力，总是零。

这意味着保守力对物体的位移所做的功只依赖于起点和终点，而与具体路径无关。

保守力的基本概念包括以下几个要点：1. 保守力与势能的关系：保守力可以用势能来描述和计算。

势能是对物体在某个力场中位置所储存的能量，而保守力则是通过势能的梯度来定义和推导的。

具体来说，对于一个保守力F，其对应的势能函数为U，满足F = -∇U。

这里的负号表示力是势能的负梯度方向，即力的方向指向势能减小的方向。

2. 势能的引入：为了便于描述和计算保守力对物体的作用，我们引入了势能这一概念。

势能可以是位置的函数，也可以是速度和其他物理量的函数。

通过引入势能，我们可以将关于保守力的问题转化为寻找势能函数和利用势能函数进行计算的问题。

保守力的基本概念包括了与势能的关系和势能的引入。

这些概念在物理学中有着广泛的应用和重要性，对于解决各种运动和相互作用问题都起着至关重要的作用。

保守力和非保守力关系的简答题保守力和非保守力是物体受到的两类力，它们在物理过程中起着重要的作用。

保守力是指在物体的位移过程中所做的功与路径无关，只与起点和终点的位置有关的力。

具体而言，在一个闭合环路中，如果一个力沿着任意一条路径绕回起点所做的功为零，则这个力是保守力。

反之，非保守力则是指在物体的位移过程中，所做功与路径有关的力。

保守力与非保守力的主要区别在于所做的功是否与路径有关。

对于保守力，物体在环路中的位移过程中，不论物体沿着怎样的路径运动，当回到起点时所做的功都是相同的。

换句话说，保守力是沿闭合环路的势能之梯度施加的，其中势能是由于位置而产生的。

例如，重力和弹簧力是典型的保守力。

在这些情况下，物体在环路中的总机械能始终保持不变。

非保守力与保守力不同，所做的功与路径有关。

不同的路径导致了所做的功的差异。

典型的非保守力包括摩擦力、阻力和涡旋力等。

摩擦力在物体相对于另一个表面移动时产生热量，所以它不是沿着闭合环路所做的，因此不是保守力。

涡旋力是一种旋转的非保守力，例如涡旋状流体中的湿气漩涡。

阻力是运动物体所受到的空气或流体的阻碍力，它同样也是非保守力。

保守力和非保守力之间存在一定的关系。

首先，任何一个非保守力可以被视为多个保守力的总和。

这是因为非保守力是路径相关的，可以通过微分位移的积分来计算相对于起点的总工作量。

而在每个微分位移中，可以将非保守力分解为垂直于位移方向的保守力和与位移方向平行的非保守力的两个分量。

这样，通过对各个微分位移的作用力进行积分，可以得到总的作用力，即非保守力。

另外，保守力和非保守力都可以通过势能来描述。

保守力是由势能施加的力，而非保守力没有明确定义的势能。

对于保守力，势能可以通过对力的势能函数进行积分得到。

当力是非保守力时，由于无法定义势能，因此无法使用势能来描述非保守力。

总的来说，保守力和非保守力是两种不同类型的力，它们在物体的位移过程中起着不同的作用。

保守力与物体的机械能有关，而非保守力则会改变物体的机械能。

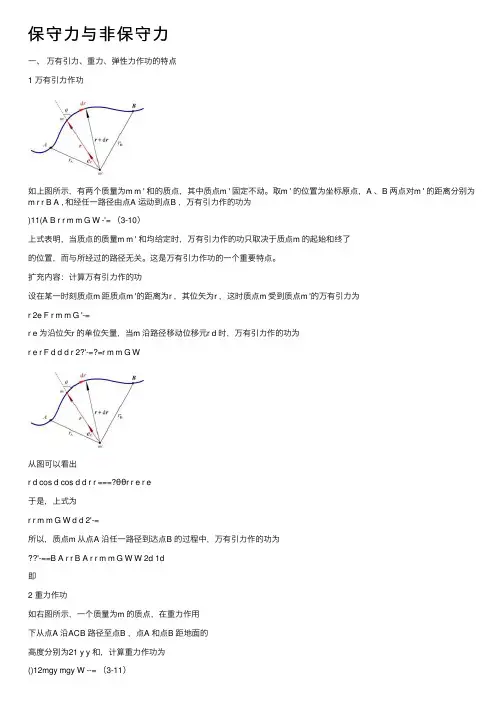
保守⼒与⾮保守⼒⼀、万有引⼒、重⼒、弹性⼒作功的特点1 万有引⼒作功如上图所⽰，有两个质量为m m ' 和的质点，其中质点m ' 固定不动。

取m ' 的位置为坐标原点，A 、B 两点对m ' 的距离分别为m r r B A , 和经任⼀路径由点A 运动到点B ，万有引⼒作的功为)11(A B r r m m G W -'= （3-10）上式表明，当质点的质量m m ' 和均给定时，万有引⼒作的功只取决于质点m 的起始和终了的位置，⽽与所经过的路径⽆关。

这是万有引⼒作功的⼀个重要特点。

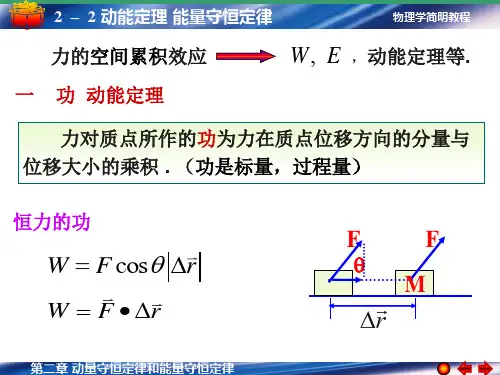
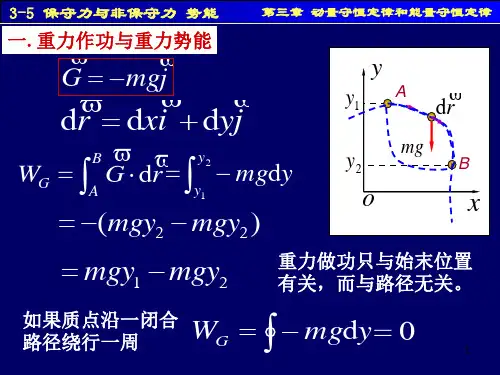
扩充内容：计算万有引⼒作的功设在某⼀时刻质点m 距质点m '的距离为r ，其位⽮为r ，这时质点m 受到质点m '的万有引⼒为r 2e F r m m G '-=r e 为沿位⽮r 的单位⽮量，当m 沿路径移动位移元r d 时，万有引⼒作的功为r e r F d d d r 2?'-=?=r m m G W从图可以看出r d cos d cos d d r r ===?θθr r e r e于是，上式为r r m m G W d d 2'-=所以，质点m 从点A 沿任⼀路径到达点B 的过程中，万有引⼒作的功为'-==B A r r B A r r m m G W W 2d 1d即2 重⼒作功如右图所⽰，⼀个质量为m 的质点，在重⼒作⽤下从点A 沿ACB 路径⾄点B ，点A 和点B 距地⾯的⾼度分别为21 y y 和，计算重⼒作功为()12mgy mgy W --= （3-11）上式表明，重⼒作功只与质点的起始和终了位置有关，⽽与所经过的路径⽆关，这是重⼒作功的⼀个重要特点。

扩充内容：计算重⼒作的功因为质点运动的路径为⼀曲线，所以重⼒和质点运动⽅向之间的夹⾓是不断变化的。

我们把路径ACB 分成许多位移元，在位移元r d 中，重⼒P 所作的功为r P d d ?=W若质点在平⾯内运动，按图所选坐标，并取地⾯上某⼀点为坐标原点O ，有j i r y x d d d +=且j P mg -=。

电势能的保守性质和非保守性质电势能是物体在电场中由于位置发生变化而具有的能量。

在物理学中，电势能可以分为保守性质和非保守性质两类。

本文将详细探讨电势能的这两种性质。

一、电势能的保守性质保守性质是指电势能在一个闭合路径上的变化与路径无关。

换句话说，无论物体如何从起点到终点经过怎样的路径，最终的电势能的变化都是相同的。

这种性质与电场的势能相关。

1.1 等势面和等势线在静电场中，电势能与电场强度成正比。

等势面是指在任意一点上具有相同电势能的点所组成的曲面，其通常被认为是一个密闭曲面。

而等势线则表示相同电势能的点在二维平面上的连续曲线。

1.2 电势能与电位的关系电势能与电场强度之间存在着直接的关系。

在电场中，电势能的变化量等于电荷在电场中移动的过程中所进行的功。

而电场中单位正电荷所具有的电势能称为电势，常用符号V表示。

因此，电势能的改变可以通过电位差来描述。

1.3 路径独立性定理路径独立性定理是电势能保守性质的重要推论。

它指出，在保守力场中，完成从一个位置到另一个位置的电势能变化只与这两个位置有关，与路径无关。

这一定理为我们计算电势能变化提供了极大的便利。

二、电势能的非保守性质与电势能的保守性质不同，非保守性质是指电势能在一个闭合路径上的变化与路径有关。

这种性质与与摩擦力、涡旋电场等相关。

2.1 摩擦力与非保守性质在存在有摩擦力的情况下，物体移动的路径会影响其电势能的变化。

由于摩擦力的存在，物体在移动的过程中会损失部分电势能，而这个损失的能量会转化为其他形式的能量，如热能。

2.2 非保守力与非保守性质在电场中，非保守力也会影响电势能的变化。

非保守力是指与路径相关的力，如摩擦力和涡旋电场。

当物体在非保守力的作用下移动时，电势能的变化将与路径有关，从而呈现出非保守性质。

2.3 路径依赖性定理路径依赖性定理是体现电势能非保守性质的一个重要原理。

它指出，在非保守力场中，完成从一个位置到另一个位置的电势能变化与路径有关，不同的路径将导致不同的电势能变化。

第四章 动能和势能（2）学习内容： 4.4 保守力与非保守力 势能 4.5 功能原理和机械能守恒定律所做的工作：1.学习力场，保守力，非保守力势能等概念。

2.讨论机械能的 变化规律――功能原理和机械能守恒定律。

4.4 保守力与非保守力，势能。

在力学中，一谈到动能，往往同时需要考虑物体的势能。

势能概念是在 保守力概念基础上提出的。

所以在具体讨论势能概念之前我们先来学习力场，保守力和非保守力等概念。

（一） 力场一般情况下，质点所收到的外力可表现为：(,,)F F t r v = （1）如果F 只与质点的位置有关，即 ()(,,)V F r F x y z ==（2）则称F 为场力，即F 为空间坐标的单值矢量函数并 把场力F 存在的空间叫做力场。

物理“场”――物质存在的一种形式。

它具有动量和能量。

在经典理学中认为：力具有超距作用，力场概念仅限于（2）式所描述的力场。

常见的力场有：○1重力场，且在不太大的 时间◎◎◎ 范围内有场力：*F maW mg =-=W mg =＝恒量 ○2静电场：静电场力（库仑力） ：314q qF r r οοε=∏电场强度：314q E r rοοε=∏ ○3平行板电容器中的静电场 场强：E =恒量F`（x ，y ，z ） YXF （x ，y ，z ）RR` Z○4弹簧弹性力――――场力显然，○2和○4两种情况下，质点所受力的作用线始终通过某一固定点，称该力为有心力，并称该O 为力心。

另外，上述各力都只与质点的位置有关，所以，都是场力。

与此相反：洛仑兹力 F q E q V B =+⨯ 与V 有关摩镲力：F kV =-或F N μ=非主动力，由运动状态及其他外力而定。

都不是场力。

加速参考系的惯性力：*F ma =- 与 W m g =相类似。

离心惯性力：()()bx y a A F ar F i F j axi ayj ==++⎰⎰*2f mv r λ=- ⇒有心力科氏奥里力 *`2k f mv ω=⨯ 不是场力。