保守力与非保守力
- 格式:doc
- 大小:165.50 KB
- 文档页数:7

保守力与非保守力Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】非保守力:凡作功与路径有关的力称为非保守力。
常见的摩擦力,物体间相互作非弹性碰撞时的冲击力都属于非保守力。
非保守力具有沿任意闭合路径作功不等于零的特点。
非保守力包括耗散力和非耗散力两类。
在力学范围内接触的非保守力大多数是耗散力,所以长期以来耗散力就成了非保守力的同义词。
严格说来两者是有区别的,一个系统的总机械能减少,并转变为系统的热能或内能。
通常人们把这个过程叫耗散过程,而把导致耗散的力成为耗散力。
摩擦力是耗散力,但非保守力(如爆炸力)不一定都是耗散力。
⑴定义:做功多少只由始末位置所决定,而跟路径无关的力叫做保守力。
做功多少和物体运动路径有关的力叫耗散力。
⑵说明①保守力对物体做功的多少取决于物体始末位置,如果在该力作用下,物体的运动沿闭合路线绕行一周回到了起始位置,则所做功为零。
重力、弹力等属于保守力。
耗散力做功就不能由物体的始末位置决定,而和物体的运动路径有关,在其他条件相同的情况下,物体运动路径越长,所做的功也越多。
摩擦力、粘滞力等属于耗散力②保守力和耗散力所做功的情况不同,是和这两种力的本身的特点有关。
物体系确定后保守力和物体的运动状况无关,其大小由相互作用物体的相对位置所确定,它的方向总在两个相互作用物体的连线上。
例如,物体确定后,重力的大小决定于它离开地面的高度,方向竖直向下,而和物体以什么样的速度运动无关,和物体运动速度的大小和方向如何变化无关。
耗散力的大小和方向都随着物体运动速度的大小、方向的改变而发生变化。
例如,空气对运动物体的阻力,其方向随着物体运动的方向改变而变化,它的大小随物体运动速度增大而增加。
③保守力和物体系的势能有着极为密切的联系。
保守力做正功,则物体系的势能减少;反之,则物体系的势能增加。
而且相对两个位置之间,功量一定,能量差一定。
所以物体间存在保守力是物体系具有势能的条件。

非保守力:凡作功与路径有关的力称为非保守力。
常见的摩擦力,物体间相互作非弹性碰撞时的冲击力都属于非保守力。
非保守力具有沿任意闭合路径作功不等于零的特点。
非保守力包括耗散力和非耗散力两类。
在力学范围内接触的非保守力大多数是耗散力,所以长期以来耗散力就成了非保守力的同义词。
严格说来两者是有区别的,一个系统的总机械能减少,并转变为系统的热能或内能。
通常人们把这个过程叫耗散过程,而把导致耗散的力成为耗散力。
摩擦力是耗散力,但非保守力(如爆炸力)不一定都是耗散力。
⑴定义:做功多少只由始末位置所决定,而跟路径无关的力叫做保守力。
做功多少和物体运动路径有关的力叫耗散力。
⑵说明①保守力对物体做功的多少取决于物体始末位置,如果在该力作用下,物体的运动沿闭合路线绕行一周回到了起始位置,则所做功为零。
重力、弹力等属于保守力。
耗散力做功就不能由物体的始末位置决定,而和物体的运动路径有关,在其他条件相同的情况下,物体运动路径越长,所做的功也越多。
摩擦力、粘滞力等属于耗散力②保守力和耗散力所做功的情况不同,是和这两种力的本身的特点有关。
物体系确定后保守力和物体的运动状况无关,其大小由相互作用物体的相对位置所确定,它的方向总在两个相互作用物体的连线上。
例如,物体确定后,重力的大小决定于它离开地面的高度,方向竖直向下,而和物体以什么样的速度运动无关,和物体运动速度的大小和方向如何变化无关。
耗散力的大小和方向都随着物体运动速度的大小、方向的改变而发生变化。
例如,空气对运动物体的阻力,其方向随着物体运动的方向改变而变化,它的大小随物体运动速度增大而增加。
③保守力和物体系的势能有着极为密切的联系。
保守力做正功,则物体系的势能减少;反之,则物体系的势能增加。
而且相对两个位置之间,功量一定,能量差一定。
所以物体间存在保守力是物体系具有势能的条件。
系统的各物体在只受保守力作用的情况下其机械能守恒。
耗散力不象保守力,对于两个位置之间,力对物体做功没有确定的值,从而相应的两个位置之间没有一定的能量差。




保守力和非保守力关系的简答题保守力和非保守力是物体受到的两类力,它们在物理过程中起着重要的作用。
保守力是指在物体的位移过程中所做的功与路径无关,只与起点和终点的位置有关的力。
具体而言,在一个闭合环路中,如果一个力沿着任意一条路径绕回起点所做的功为零,则这个力是保守力。
反之,非保守力则是指在物体的位移过程中,所做功与路径有关的力。
保守力与非保守力的主要区别在于所做的功是否与路径有关。
对于保守力,物体在环路中的位移过程中,不论物体沿着怎样的路径运动,当回到起点时所做的功都是相同的。
换句话说,保守力是沿闭合环路的势能之梯度施加的,其中势能是由于位置而产生的。
例如,重力和弹簧力是典型的保守力。
在这些情况下,物体在环路中的总机械能始终保持不变。
非保守力与保守力不同,所做的功与路径有关。
不同的路径导致了所做的功的差异。
典型的非保守力包括摩擦力、阻力和涡旋力等。
摩擦力在物体相对于另一个表面移动时产生热量,所以它不是沿着闭合环路所做的,因此不是保守力。
涡旋力是一种旋转的非保守力,例如涡旋状流体中的湿气漩涡。
阻力是运动物体所受到的空气或流体的阻碍力,它同样也是非保守力。
保守力和非保守力之间存在一定的关系。
首先,任何一个非保守力可以被视为多个保守力的总和。
这是因为非保守力是路径相关的,可以通过微分位移的积分来计算相对于起点的总工作量。
而在每个微分位移中,可以将非保守力分解为垂直于位移方向的保守力和与位移方向平行的非保守力的两个分量。
这样,通过对各个微分位移的作用力进行积分,可以得到总的作用力,即非保守力。
另外,保守力和非保守力都可以通过势能来描述。
保守力是由势能施加的力,而非保守力没有明确定义的势能。
对于保守力,势能可以通过对力的势能函数进行积分得到。
当力是非保守力时,由于无法定义势能,因此无法使用势能来描述非保守力。
总的来说,保守力和非保守力是两种不同类型的力,它们在物体的位移过程中起着不同的作用。
保守力与物体的机械能有关,而非保守力则会改变物体的机械能。

非保守力判定条件非保守力是物理学中的基本概念之一,它是指作用在物体上的力不是仅仅沿着物体的运动方向而同向的力。
简单来说,非保守力是指摩擦力、阻力等不能被完全恢复的力。
在物理学中,非保守力和保守力是两个非常重要的概念。
保守力是指沿着物体运动方向而同向的力,它所做的功可以通过路径和初始位置以及最终位置来确定。
而非保守力则恰好相反,它所做的功不能通过路径和初始位置以及最终位置来唯一确定。
因此,我们需要特定的判定条件来鉴定一个力是否是非保守力。
下面,我们将介绍一些常见的非保守力判定条件:1. 路径导致能量损失。
当力沿着物体的运动方向施加时,物体在相应方向上获得了能量,但当力沿着不同于物体运动方向的方向施加时,会导致物体的能量损失。
2. 动能和势能不守恒。
对于保守力,动能和势能的总和是守恒的。
但对于非保守力,由于能量被耗散,势能和动能不再守恒。
3. 动能和功无法相等。
对于保守力,动能和所做的功是相等的。
但对于非保守力,由于能量被耗散,动能和所做的功不再相等。
4. 功与路径有关。
由于非保守力的性质,它所做的功取决于物体的运动路径。
当路径改变时,功的大小也会随之改变。
在实际应用中,我们需要特定的判定条件来识别一个力是否是非保守力。
了解非保守力的特征和判定条件对物理学的深入理解至关重要。
总而言之,非保守力是物理学中的基本概念之一,它与保守力是相对应的,两者具有不同的特征和属性。
通过上述介绍的非保守力判定条件,我们可以更好的认识和理解非保守力的本质特征,丰富我们物理学知识的储备,为我们掌握科学知识提供了很好的启示。

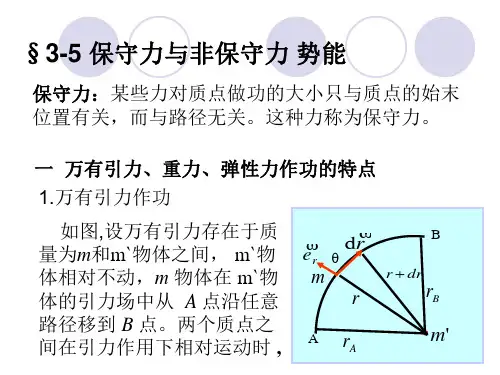
保守⼒与⾮保守⼒⼀、万有引⼒、重⼒、弹性⼒作功的特点1 万有引⼒作功如上图所⽰,有两个质量为m m ' 和的质点,其中质点m ' 固定不动。
取m ' 的位置为坐标原点,A 、B 两点对m ' 的距离分别为m r r B A , 和经任⼀路径由点A 运动到点B ,万有引⼒作的功为)11(A B r r m m G W -'= (3-10)上式表明,当质点的质量m m ' 和均给定时,万有引⼒作的功只取决于质点m 的起始和终了的位置,⽽与所经过的路径⽆关。
这是万有引⼒作功的⼀个重要特点。
扩充内容:计算万有引⼒作的功设在某⼀时刻质点m 距质点m '的距离为r ,其位⽮为r ,这时质点m 受到质点m '的万有引⼒为r 2e F r m m G '-=r e 为沿位⽮r 的单位⽮量,当m 沿路径移动位移元r d 时,万有引⼒作的功为r e r F d d d r 2?'-=?=r m m G W从图可以看出r d cos d cos d d r r ===?θθr r e r e于是,上式为r r m m G W d d 2'-=所以,质点m 从点A 沿任⼀路径到达点B 的过程中,万有引⼒作的功为'-==B A r r B A r r m m G W W 2d 1d即2 重⼒作功如右图所⽰,⼀个质量为m 的质点,在重⼒作⽤下从点A 沿ACB 路径⾄点B ,点A 和点B 距地⾯的⾼度分别为21 y y 和,计算重⼒作功为()12mgy mgy W --= (3-11)上式表明,重⼒作功只与质点的起始和终了位置有关,⽽与所经过的路径⽆关,这是重⼒作功的⼀个重要特点。
扩充内容:计算重⼒作的功因为质点运动的路径为⼀曲线,所以重⼒和质点运动⽅向之间的夹⾓是不断变化的。
我们把路径ACB 分成许多位移元,在位移元r d 中,重⼒P 所作的功为r P d d ?=W若质点在平⾯内运动,按图所选坐标,并取地⾯上某⼀点为坐标原点O ,有j i r y x d d d +=且j P mg -=。
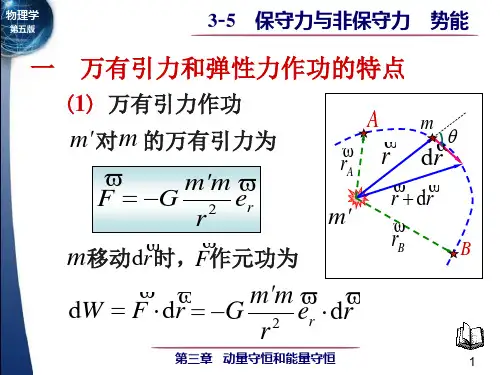
一、万有引力、重力、弹性力作功的特点1 万有引力作功如上图所示,有两个质量为m m ' 和的质点,其中质点m ' 固定不动。
取m ' 的位置为坐标原点,A 、B 两点对m ' 的距离分别为m r r B A , 和经任一路径由点A 运动到点B ,万有引力作的功为)11(A B r r m m G W -'= (3-10)上式表明,当质点的质量m m ' 和均给定时,万有引力作的功只取决于质点m 的起始和终了的位置,而与所经过的路径无关。
这是万有引力作功的一个重要特点。
扩充内容:计算万有引力作的功设在某一时刻质点m 距质点m '的距离为r ,其位矢为r ,这时质点m 受到质点m '的万有引力为r 2e F r m m G '-=r e 为沿位矢r 的单位矢量,当m 沿路径移动位移元r d 时,万有引力作的功为r e r F d d d r 2⋅'-=⋅=rm m G W从图可以看出rd cos d cos d d r r ===⋅θθr re r e 于是,上式为r r m m G W d d 2'-= 所以,质点m 从点A 沿任一路径到达点B 的过程中,万有引力作的功为⎰⎰'-==B A r r B A r r m m G W W 2d 1d 即2 重力作功如右图所示,一个质量为m 的质点,在重力作用下从点A 沿ACB 路径至点B ,点A 和点B 距地面的高度分别为21 y y 和,计算重力作功为()12mgy mgy W --= (3-11)上式表明,重力作功只与质点的起始和终了位置有关,而与所经过的路径无关,这是重力作功的一个重要特点。
扩充内容: 计算重力作的功因为质点运动的路径为一曲线,所以重力和质点运动方向之间的夹角是不断变化的。
我们把路径ACB 分成许多位移元,在位移元r d 中,重力P 所作的功为rP d d ⋅=W若质点在平面内运动,按图所选坐标,并取地面上某一点为坐标原点O ,有ji r y x d d d += 且j P mg -=。
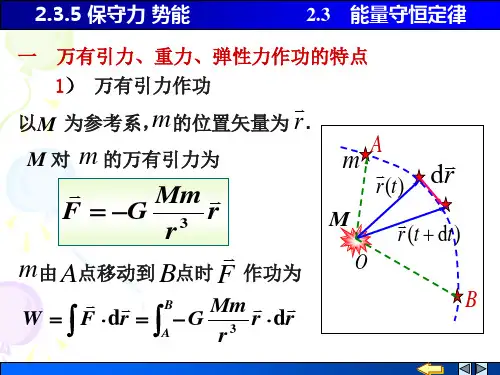
一、 万有引力、重力、弹性力作功的特点
1 万有引力作功
如上图所示,有两个质量为m m ' 和的质点,其中质点m ' 固定不动。
取m ' 的位置为坐标原点,A 、B 两点对m ' 的距离分别为m r r B A , 和经任一路径由点A 运动到点B ,万有引力作的功为
)11(A B r r m m G W -'= (3-10)
上式表明,当质点的质量m m ' 和均给定时,万有引力作的功只取决于质点m 的起始和终了
的位置,而与所经过的路径无关。
这是万有引力作功的一个重要特点。
扩充内容:计算万有引力作的功
设在某一时刻质点m 距质点m '的距离为r ,其位矢为r ,这时质点m 受到质点m '的万有引力为
r 2e F r m m G '-=
r e 为沿位矢r 的单位矢量,当m 沿路径移动位移元r d 时,万有引力作的功为
r e r F d d d r 2⋅'-=⋅=r m m G W
从图可以看出
r d cos d cos d d r r ===⋅θθr r e r e
于是,上式为
r r m m G W d d 2'-=
所以,质点m 从点A 沿任一路径到达点B 的过程中,万有引力作的功为
⎰⎰'-==B A r r B A r r m m G W W 2d 1d
即
2 重力作功
如右图所示,一个质量为m 的质点,在重力作用
下从点A 沿ACB 路径至点B ,点A 和点B 距地面的
高度分别为21 y y 和,计算重力作功为
()12mgy mgy W --= (3-11)
上式表明,重力作功只与质点的起始和终了位置
有关,而与所经过的路径无关,这是重力作功的一个
重要特点。
扩充内容: 计算重力作的功
因为质点运动的路径为一曲线,所以重力和质点运动方向之间的夹角是不断变化的。
我们把路径ACB 分成许多位移元,在位移元r d 中,重力P 所作的功为
r P d d ⋅=W
若质点在平面内运动,按图所选坐标,并取地面上某一点为坐标原点O ,有
j i r y x d d d +=
且j P mg -=。
于是,前式为
y mg y x mg W d )d d ( d -=+⋅-=j i j
质点由点A 移至点B 的过程中,重力作的总功为
)(d 12 21y y mg y mg W y y --=-=⎰
即
)(12mgy mgy W --=
3 弹性力作功
下图所示是一放置在光滑平面上的弹簧,弹簧的一端固定,另一端与一质量为m 的物体相连接。
当弹簧在水平方向不受外力作用时,它将不发生形变,此时物体位于点O (即位于0
=x
处),这个位置叫做平衡位置。
现以平衡位置O 为坐标原点,向右为Ox 轴正向。
弹簧伸长量由1x 变到2x 时,计算弹性力对物体的作的功为
)2121(2122kx kx W --= (3-12)
式中k 为弹簧的劲度系数。
从式(3-12)可以看出,对在弹性限度内具有给定劲度系数的弹簧来说,弹性力作的功只由弹簧起始和终了的位置(1x 和2x )决定,而与弹性形变的过程无关。
扩充内容: 计算弹性力对物体所作的功
若物体受到沿Ox 轴正向的外力F '作用,弹簧将沿Ox 轴正向被拉长,弹簧的伸长量即其位移为x 。
根据胡克定律,在弹性限度内,弹簧的弹性力F 与弹簧的伸长量x 之间的关系为
i F kx -=
式中k 称为弹簧的劲度系数。
在弹簧被拉长的过程中,弹性力是变力。
但弹簧位移为x d 时的弹性力F 可近似看成是不变的。
于是,弹簧位移为x d 时,弹性力作的元功为
i i i i x F ⋅-=⋅-=⋅=x kx x kx W d d d d
有
x kx W d d -=
这样,弹簧的伸长量由21 x x 变到时,弹性力所作的功就等于各个元功之和。
由积分计算可得
⎰⎰-==21 d d x x x x k W W
二、 保守力与非保守力 保守力作功的数学表达式
从上述对重力、万有引力和弹性力作功的讨论中可以看出,它们所作的功只与物体(或弹簧)的始、末位置有关,而与路径无关。
这是它们作功的一个共同特点。
我们把具有这种特点的力叫做保守力。
除了上面所讲的重力、万有引力和弹性力是保守力外,电荷间相互作用的库仑力和原子间相互作用的分子力也是保守力(参阅第6-1节和第7-5节)。
保守力作功与路径无关的特性还可以用另一种方式来表示:物体沿任意闭合路径运动一周时,保守力对它作功为零,即
⎰=⋅=0d r F W (3-13)
式(3-13)是反映保守力作功特点的数学表达式。
然而,在物理学中并非所有的力都具有作功与路径无关这一特点,例如常见的摩擦力,它所作的功就与路径有关,路径越长,摩擦力作的功也越大。
显然,摩擦力就不具有保守力作功的特点。
我们把这种作功与路径有关的力叫做非保守力。
三、势能
1 从上面关于万有引力、重力和弹性力作功的讨论中,我们知道这些保守力作功均只与物体的始末位置有关,为此,可以引入势能概念。
我们把与物体位置有关的能量称作物体的势能,用符号P E 表示。
于是,三种势能分别为
重力势能 mgy E =P
引力势能 r m m G
E '-=P (3-14) 弹性势能 2P 21kx E =
式(3-10)、式(3-11)、和式(3-12)可统一写成
P P1P2)(E E E W ∆-=--= (3-15)
上式表明,保守力对物体作的功等于物体势能增量的负值。
2 对势能概念的进一步讨论
讨论:
1重力势能 (通常把质点在地球表面附近的引力势能叫做重力势能)
设地球半径为E R ,质量为E m 。
质点m 处在地球表面h 处,与处在地球表面处的引力势能之差为
)11(
)()(E E E E P E P R h R Gmm R E h R E -+-=-+
)(E E E h R R h Gmm +=
由于质点m 放在地球表面附近,故2E E E )(R h R R ≈+,上式可近似写成
h R mm G R E h R E 2E E
E P E P )()(≈-+
由于地球表面附近重力加速度的值2E E /R Gm g =,且取地球表面作为重力势能零点,即
0)(E P =R E ,那么从上式可得质点在地球表面h 处的引力势能即重力势能为
mgh h R E =+)(E P
可见,改变引力势能零点,引力势能的表述式也改变了。
2势能的进一步讨论
(1)势能是状态的函数。
在保守力作用下,只要物体的起始和终了位置确定了,保守力所作的功也就确定了,而与所经过的路径是无关的。
所以说,势能是坐标函数,亦即是状态的函数,
即),,(P P z y x E E =。
前面还说过,动能亦是状态的函数,),,(z y x k k v v v E E =。
(2)势能的相对性。
势能的值与势能零点的选取有关。
一般选地面的重力势能为零,引力势能的零点取在无限远处,而水平放置的弹簧处于平衡位置时,其弹性势能为零。
当然,势能零点也可以任意选取,选取不同的势能零点,物体的势能就将具有不同的值。
所以,通常说势能具有相对意义。
但也应当注意,任意两点间的势能之差却是具有绝对性的。
(3)势能是属于系统的。
势能是由于系统内各物体间具有保守力作用而产生的。
因而它是属于系统的。
单独谈单个物体的势能是没有意义的。
例如重力势能就是属于地球和物体所组成的系统的。
如果没有地球对物体的作用,也就谈不上重力作功和重力势能问题,离开了地球作用范围的宇宙飞船,也就无所谓重力势能。
同样,弹性势能和引力势能也是属于有弹性力和引力作用的系统的。
应当注意,在平常叙述时,常将地球与物体系统的重力势能说成是物体的,这只是为了叙述上的简便,其实它是属于地球和物体系统的。
至于物体的引力势能和弹性势能,也都是这样。
四、思考题
1.保守力作的功总是负的,对吗?举例说明。
2、把物体抛向空中,有哪些力对它作功,这些力是否都是保守力?。