大学物理 第三章 动量守恒定律和能量守恒定律 3-5 保守力与非保守力
- 格式:ppt
- 大小:478.50 KB
- 文档页数:18



第三章 动量守恒定律和能量守恒定律概述:1、牛顿第二定律描述了力对物体作用的瞬间关系,物体瞬间获得响应的加速度,物体的运动状态已经开始发生变化,要使物体的运动状态继续变化,需要力的作用有一个过程。
本章从力的空间累积效应和时间累积效应出发,用动量和能量对机械运动进行分析。
2、由对一个质点的研究过渡到质点系的研究。
3、守恒定律是完美、和谐的自然界的体现。
动量守恒和能量守恒源于牛顿力学,但在牛顿定律不适用的领域,例如微观粒子及高能物理领域仍然适用,故它是自然界的一条基本定律。
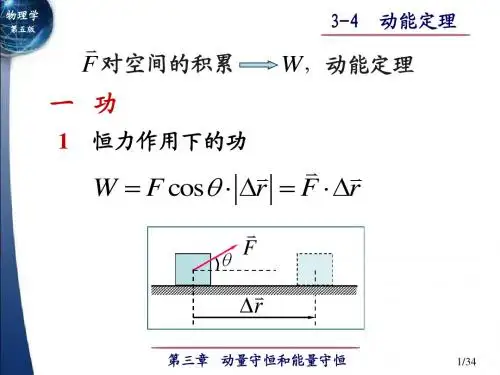
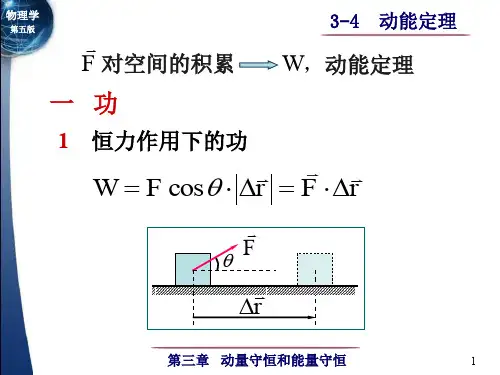
3-1质点和质点系的动量定理一、 冲量 质点的动量定理牛顿第二定律的微分形式d d t =pF d d t =F p 22112121d t d t t m m ==-⎰⎰p p F p p p =υ-υ1.冲量:力对时间的积分,常以I 表示,并称⎰=21d t t t F I为在1t ~2t 时间内、力F 对质点的冲量,或简单说成F 的冲量。
说明:(1).冲量,是一个矢量,大小为21d t t t =⎰I F ,方向是速度或动量的变化方向。
(2).由于冲量是作用力的时间积分,必须知道力在这段时间中的全部情况,才能求出冲量。
实际上要知道力的大小和方向随时间变化是很困难的,必须采取近似处理。
F 为恒力(方向也不变)时,t =∆I F ;(高中的冲量定义) F 作用时间很短时,可用力的平均值F 来代替。
211d t t t t =∆⎰F F ,21t t t ∆=-2.动量(p )是描述物体运动状态的物理量,有大小和方向,是一个矢量。
方向和运动速度的方向相同。
单位:㎏·m/s量纲:MLT -1。
3.质点的动量定理:在给定的时间间隔内,质点所受合力的冲量,等于该质点动量的增量。
22112121d t d t t m m ==-⎰⎰p p F p p p =υ-υ在直角坐标系中,质点的动量定理的分量形式:212121212121---t x x x xt t y y y y t t z zz zt I F dt m υm υI F dt m υm υI F dt m υm υ⎧==⎪⎪⎪==⎨⎪⎪==⎪⎩⎰⎰⎰动量定理在打击和碰撞等情形中特别有用。

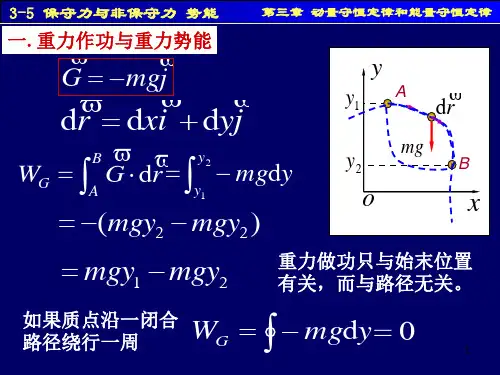


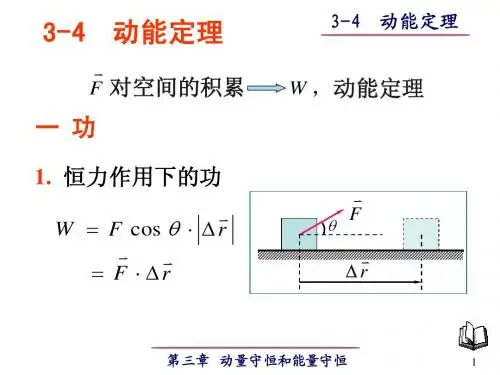
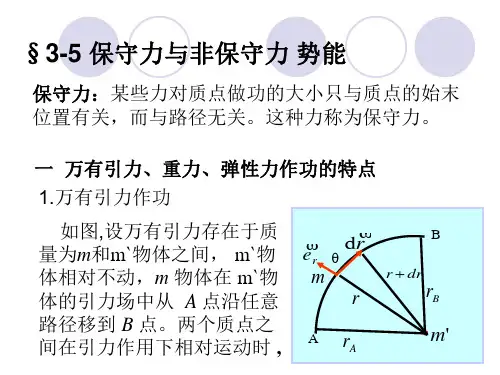
3 – 5 保守力与非保守力 势能第三章动量守恒定律和能量守恒定律一 万有引力、重力、弹性力作功的特点v m 以m' 为参考系, 的位置矢量为 r . m' 对 m 的万有引力为v m' m v F = −G 3 r r1) 万有引力作功mm'A v r (t)v drv m 由 A点移动到 B点时 Fv r (t + dt)O作功为v v B m' m v v W = ∫ F ⋅ d r = ∫ − G 3 r ⋅ dr A rB3 – 5 保守力与非保守力 势能第三章动量守恒定律和能量守恒定律v v B m' m v v W = ∫ F ⋅ dr = ∫ − G 3 r ⋅ dr A rmm'OA v r (t)v drv r (t + dt)B⎡ m' m m' m ⎤ ) − (−G )⎥ W = −⎢(−G rB rA ⎦ ⎣v v v rdr = ϕ soc rd r = rd ⋅ rm' m W = ∫ − G 2 dr rA rrBv r (t )v drv r (t + dt ) ϕ3 – 5 保守力与非保守力 势能第三章动量守恒定律和能量守恒定律v v P = − mg k v v v v d r = d x i + d yj + d zkW =∫B A2 ) 重力作功v v zB P ⋅ d r = ∫ − mg dzzAzAzAzBmgB= − ( mgz B − mgz A )W = − mg d z = 0 ∫oxy3 – 5 保守力与非保守力 势能第三章动量守恒定律和能量守恒定律3 ) 弹性力作功v FoxxAxB xAxBxB xAv v F = − kx iW = ∫ Fdx = ∫ − kxdx1 2 1 2 W = −( kxB − kx A ) 2 2W = ∫ − kxdx = 03 – 5 保守力与非保守力 势能第三章动量守恒定律和能量守恒定律二 保守力和非保守力 保守力: 力所作的功与路径无关,仅决定于相 互作用质点的始末相对位置 . 引力功 重力功W = − ( mgz B − mgz A ) 1 2 1 2 弹力功 W = − ( kx B − kx A ) 2 2⎡ m' m ⎤ m' m ) − ( −G )⎥ W = − ⎢ ( −G rA ⎦ rB ⎣AC∫ACBv v F ⋅ dr = ∫ADBv v F ⋅ drD B3 – 5 保守力与非保守力 势能第三章动量守恒定律和能量守恒定律∫lACBv v F ⋅ dr = ∫ACBADBv v F ⋅ drv v F ⋅ drACv v ∫ F ⋅ dr = ∫v v F ⋅ dr + ∫D BACBDAv v ∫ F ⋅ dr = 0lD B物体沿闭合路径运动 一周时, 保守力对它所作的功等于零 . 非保守力: 力所作的功与路径有关 .(例如摩擦 力)3 – 5 保守力与非保守力 势能第三章动量守恒定律和能量守恒定律三 势能 势能 重力功与物体间相互作用及相对位置有关的能量 . 重力势能W = −(mgzB − mgzA )引力功 ⎡ m' m m' m ⎤ ) − (−G )⎥ W = −⎢(−G rB rA ⎦ ⎣ 弹力功 引力势能E p = mgzm' m Ep = −G r 弹性势能 1 2 E p = kx 21 2 1 2 W = − ( kx B − kx A ) 2 2保守力的功W = − ( E p 2 − E p1 ) = − ∆ E P3 – 5 保守力与非保守力 势能第三章动量守恒定律和能量守恒定律讨论势能是状态函数Ep = Ep ( x, y , z )势能具有相对性,势能大小与势能零点的选取有关 . 势能是属于系统的 . 势能计算 令W = − ( E p − E p0 ) = − ∆ E pEp0 = 0 E p ( x , y , z ) =∫E p0 = 0( x, y,z)v v F ⋅ dr3 – 5 保守力与非保守力 势能第三章动量守恒定律和能量守恒定律四 势能曲线E p = mgzEp1 2 E p = kx 2m' m Ep = −G rEpOEpxOzOx弹性势能曲线 引力势能曲线重力势能曲线z = 0, Ep = 0x = 0, Ep = 0r → ∞, Ep = 0。