人教A版数学必修一2.2.2《对数函数及其性质》(二)配套试题

第二课时对数函数的图象及性质的应用(习题课)【选题明细表】1.(2018·石家庄市一模)已知函数y=f(x+2)的图象关于直线x=-2对称,则当x∈(0,+∞)时,f(x)=|log2x|,若a=f(-3),b=f(),c=f(2),则a,b,c的大小关系是( B )(A)a>b>c (B)b>a>c(C)c>a>b (D)a>c>b解析:因为函数y=f(x+2)的图象关于x=-2对称,所以函数y=f(x)的图象关于y轴对称,所以函数y=f(x)是偶函数.所以a=f(-3)=f(3)=|log23|=log23,又b=f（）==|-2|=2,c=f(2)=|log22|=1,所以c<a<b.2.若函数y=f(x)与函数y=ln+1的图象关于直线y=x对称,则f(x)等于( A )(A)e2x-2(B)e2x(C)e2x+1(D)e2x+2解析:若两个函数的图象关于直线y=x对称,那么这两个函数互为反函数,而y=ln+1的反函数为y=e2x-2,故选A.3.(2018·泉州高一检测)若log m8.1<log n8.1<0,那么m,n满足的条件是( C )(A)m>n>1 (B)n>m>1(C)0<n<m<1 (D)0<m<n<1解析:由题意知m,n一定都是大于0且小于1的数,根据函数图象(图略)知,当x>1时,底数越大,函数值越小,故选C.4.已知函数f(x)=log(a-1)(2x+1)在（-,0）内恒有f(x)>0,则a的取值范围是( D )(A)(1,+∞) (B)(0,1)(C)(0,2) (D)(1,2)解析:由-<x<0,得0<2x+1<1.若f(x)>0恒成立,则0<a-1<1.所以1<a<2.故选D.5.(2018·宜昌高一期中)函数f(x)=lo(x2-2x)的单调递增区间是( D )(A)(1,+∞) (B)(2,+∞)(C)(-∞,1) (D)(-∞,0)解析:函数f(x)=lo(x2-2x)的定义域为(2,+∞)∪(-∞,0),设函数的单调增区间即u=x2-2x的单调减区间,u=x2-2x的单调减区间为(-∞,0).故选D.6.若函数f(x)=ln(x2+ax+1)是偶函数,则实数a的值为.解析:函数f(x)=ln(x2+ax+1)是偶函数,所以f(x)=f(-x),即ln(x2+ax+1)=ln(x2-ax+1),所以ax=-ax在函数的定义域中总成立,所以a=0.答案:07.不等式lo(4x+2x+1)>0的解集为 .解析:由lo(4x+2x+1)>0,得4x+2x+1<1,即(2x)2+2·2x<1,配方得(2x+1)2<2,所以2x<-1,两边取以2为底的对数,得x<log2(-1).答案:(-∞,log2(-1))8.已知f(x)=log4(4x-1).(1)求f(x)的定义域;(2)讨论f(x)的单调性;(3)求f(x)在区间[,2]上的值域.解:(1)由4x-1>0,解得x>0,因此f(x)的定义域为(0,+∞).(2)设0<x1<x2,则0<4x1-1<4x2-1,因此log4(4x1-1)<log4(4x2-1),即f(x1)<f(x2), 故f(x)在(0,+∞)上单调递增.(3)因为f(x)在区间[,2]上单调递增,又f()=0,f(2)=log415,因此f(x)在区间[,2]上的值域为[0,log415].9.已知log2b<log2a<log2c,则( A )(A)()b>()a>()c(B)()a>()b>()c(C)()c>()b>()a(D)()c>()a>()b解析:因为log2b<log2a<log2c,所以c>a>b,所以()b>（）a>（）c.故选A.10.(2018·哈尔滨六中一模)已知函数f(x)=则f(2+log23)等于( D )(A)8 (B)12 (C)16 (D)24解析:因为1<log23<2,所以3<2+log23<4,所以f(2+log23)=f(3+log23).又4<3+log23<5,所以f(3+log23)==23×=8×3=24.故选D.11.(2018·许昌五校高一联考)函数f(x)=log a|x-1|在(0,1)上是减函数,那么f(x)在(1,+∞)上( A )(A)递增且无最大值 (B)递减且无最小值(C)递增且有最大值 (D)递减且有最小值解析:由|x-1|>0得,函数y=log a|x-1|的定义域为{x|x≠1}.设g(x)=|x-1|=则有g(x)在(-∞,1)上为减函数,在(1,+∞)上为增函数.因为f(x)=log a|x-1|在(0,1)上是减函数,所以a>1.所以f(x)=log a|x-1|在(1,+∞)上递增且无最大值.12.(2017·兰州高一月考)已知函数f(x)=ln(ax2+2x+1).(1)若f(x)的定义域为R,求实数a的取值范围;(2)若f(x)的值域为R,求实数a的取值范围.解:(1)因为f(x)的定义域为R,所以ax2+2x+1>0恒成立.当a=0时,2x+1>0,x>-,不合题意;所以a≠0.由得a>1.故实数a的取值范围为(1,+∞).(2)因为f(x)的值域为R,所以{y|y=ax2+2x+1,x∈R}⊇(0,+∞).(也可以说y=ax2+2x+1取遍一切正数)①当a=0时,y=2x+1可以取遍一切正数,符合题意,②当a≠0时,需即0<a≤1.综上,实数a的取值范围为[0,1].13.已知f(x)=2+log3x,x∈[1,9],求y=[f(x)]2+f(x2)的最大值以及y 取最大值时x的值.解:因为f(x)=2+log3x,所以y=[f(x)]2+f(x2)=(2+log3x)2+2+log3x2=(2+log3x)2+2+2log3x=(log3x)2+6log3x+6=(log3x+3)2-3.因为函数f(x)的定义域为[1,9],所以要使函数y=[f(x)]2+f(x2)有意义,必须满足所以1≤x≤3,所以0≤log3x≤1.所以6≤y=(log3x+3)2-3≤13.当log3x=1,即x=3时,y=13.所以当x=3时,函数y=[f(x)]2+f(x2)取得最大值13.【教师备用】已知函数f(x)=log2(x+1),g(x)=log2(3x+1).(1)求出使g(x)≥f(x)成立的x的取值范围;(2)当x∈[0,+∞)时,求函数y=g(x)-f(x)的值域.解:(1)因为f(x)=log2(x+1),g(x)=log2(3x+1),g(x)≥f(x),所以3x+1≥x+1>0,所以x≥0.即使g(x)≥f(x)成立的x的取值范围为[0,+∞).(2)因为y=g(x)-f(x)=log2(3x+1)-log2(x+1)=log2(x≥0).令h(x)==3-,则h(x)为[0,+∞)上的增函数,所以1≤h(x)<3,故y=g(x)-f(x)∈[0,log23),即函数y=g(x)-f(x)的值域为[0,log23).。

文档从网络中收集，已重新整理排版.word版本可编辑:•欢迎下载支持.2. 2.2对数函数及其性质（二）课时目标1.进一步加深理解对数函数的性质.2.掌握对数函数的性质及其应用.1.函数y=log.v的图象如图所示，则实数a的可能取值是（）A. 5B.72.下列各组函数中，表示同一函数的是（）A. 和y=（心TB・y= “ 和y=xC. 和y=21og^yD・y=x和y= log^3.若函数y=f（x）的左义域是[2,4],则y=f（log丄x）的老义域是（B.[4,16]A.C.[寻,扌]D. [2,4]4.函数/(^)=10^(3^ 1)的值域为()A. (0, +8)B. [0, +8)C. (1, +8)D. [1, +8)5.函数f3=log,(x+b)(a>0且aHl)的图象经过(一1,0)和(0,1)两点，则f⑵=■6.函数y=log,(y-2) +l(a>0且aHl)恒过泄点__________________ ・一、选择题1.设a=log54t b= (log53)\ o=log t5> 则( )A. a<c<£>B. b\c<.aC. D. b\a<.c2.已知函数尸f(2j的定义域为[一1,1],则函数y=Alog>Y)的定义域为()A. [-1,1]B. [£, 2]C. [1,2]D.[住，4]3.函数f{x) =log, AV (a>0 且aHl)且f(8)=3,则有( )A. f(2)>f( —2)B. f(l)>f(2)C. f( —3)>f(—2)D. f(一3)>f(—4)4・函数f(x) =a+losAx+1)在[0, 1]上的最大值与最小值之和为a,则a的值为()A. TB. —C・ 2 D・ 44 21 ~ x5.已知函数fCv) =lg]丄丫，若f(a)=Zb则f( —a)等于( )A. b B・—b1 1C- Z D. r6.函数y=3”(一1WX0)的反函数是()A. y= log! x (x>0)3B・ j^=log3-rCv>0)C.y=logsX(*MY<l)D.y= log! x (扣Ml)3二. 填空题7.函数=l g(2x-i),若x21时，NO恒成立，则b应满足的条件是______________________ .8.函数y=log.Y当％>2时恒有|y;>l,则&的取值范弗I是 _________________ ・9.若log,2<2,则实数a的取值范围是_________________ ・三. 解答题10・已知f(0=lo乳(3—比v)在*G[0,2]上单调递减，求&的取值范围・1 ——fix11・已知函数fCv) = log| —的图象关于原点对称，其中a为常数.2 X-1(1)求a的值：(2)若当圧⑴+8)时，f3 + log](x — l)<0恒成立.求实数功的取值范围.能力提升12.设函数f{x) =log』(a>0, aH]),若fCsfZoQ =8,则f(£) +f(£) T ----------------- f(£ ow) 的值等于()A. 4 B・ 8C. 16 D・ 21ogt813・已知log fl4<log a4,比较加与n的大小.1.在对数函数y=log.Y（a>0,且aHl）中，底数a对其图象的影响无论a取何值，对数函数y=log』（a>0,且aHl）的图象均过点（1,0）,且由左义域的限制，函数图象穿过点（1,0）落在第一、四象限，随着a的逐渐增大，y=log.Y（a>b 且aHl）的图象绕（1,0）点在第一象限由左向右顺时针排列，且当0<a<l时函数单调递减，当时函数单调递增・2•比较两个（或多个）对数的大小时，一看底数，底数相同的两个对数可直接利用对数函数的单调性来比较大小，对数函数的单调性由“底”的范国决左，若“底”的范羽不明确，贝懦分“底数大于1"和“底数大于0且小于1"两种情况讨论：二看真数，底数不同但貞•数相同的两个对数可借助于图象，或应用换底公式将其转化为同底的对数来比较大小：三找中间值，底数、貞•数均不相同的两个对数可选择适当的中间值（如1或0等）来比较・2. 2.2对数函数及其性质（二）双基演练1. A2. D [y=log^=-Ylog^=^即尹=弘两函数的定义域、值域都相同.]3. C [由题意得：2Wlog“W4,所以2即討詁・]4. A [V3'+1>1, /. log2（3X+1） >0.]5. 2解析由已知得log—1） =0且log^=b.\a=b=2.从而f（2） =log：（2 + 2） =2.6.（3, 1）解析若x-2 = l,则不论a为何值，只要Q0且aHl,都有y=l・作业设计1. D [因为（Klogs3〈log&4〈l,所以A<a<c・]2. D [•••-lWxWl,/.2 即・・・y=f3的定义域为$, 2]即扣log*W2, .•.迈W点4.]3. C [•••log$=3,解得a=2,因为函数fCv)=log」％(a>0且aHl)为偶函数,且在(0, +8)为增函数，在(-oo, 0)上为减函数，由一3<-2,所以f(-3)>f(—2)・]4. B [函数fCr)=才+10劭(・丫+1),令yi = a\ 必=logsCr+l),显然在[0,1]上，y\ =/与力=log,w+1)同增或同减.因而[f3]g+[f3]^=f(l)+f(0)=a+log辽+ 14-0 = a,解得a=*.]r / 、1 + * 1—-Y5. B 0_卄1口=諒(左)齐=一3则fd)为奇函数，故f(一a) = -f(a)=-b]6. C [由y=3x(-l^K0)得反函数是r=logM*£Xl),故选C.]7.b^l解析由题意，4时,2s-b^l.又2”M2, ••"W1.8.l)U(l,2]解析V lyl>l,即力]或只一1,10ga-Y>l 或10gj-Y< —1>变形为log^Y>log^ 或log^-Klog^-当x=2时，令y|=b 则有log^= 1 或log2=-h .*.a=2 或日=£.要使02时，yl>l.如图所示，&的取值范用为1JW2或*Wa〈l.9.(0, l)U(V2, +8)解析log2<2 = log,a.若0〈a<l,由于y=log~Y是减函数，则0〈/<2,得0<&<迄,所以0<a<l：若Q1,由于y=log^是增函数，则£>2,得小迈・综上得0CN1或a>J5・10・解由Q0可知u=3—址为减函数，依题意则有a>l・又u=3 — ar在[0,2]上应满足Q0,3故3—2a>0,即a〈刁.3综上可得，a的取值范围是1<冷11・解(DY函数fG)的图象关于原点对称，•••函数f(0为奇函数./. f(~x) = —f(x),1 + a.Y 1 —a-Y x— 1即i。

2.2.2对数函数及其性质（A 卷）一、选择题（本题共8个小题）1.【题文】已知函数()2()log 1f x x -=，若()1f a =，则实数a 等于 ( ) A ．0 B ．1 C ．2 D ．32.【题文】函数()()0.25log 21f x x =-的定义域为 ( ) A.1,2⎛⎫+∞⎪⎝⎭ B.1,2⎡⎫+∞⎪⎢⎣⎭ C.11,42⎛⎤ ⎥⎝⎦ D.1,4⎛⎫+∞ ⎪⎝⎭3.【题文】给出下列函数：(1)223log y x =；(2)()3log 1y x =-；(3) πlog y x =.其中是对数函数的有 ( )A.0个B.1个C.2个D.3个 4.【题文】函数()()2log 32x f x =+的值域为 ( ) A.()0,+∞ B. [)0,+∞ C. ()1,+∞ D. [)1,+∞5.【题文】已知函数()20,log ,2,0,xx x f x x =≤>⎧⎨⎩ 若()12f a =，则实数a = ( )A.1- C.1或 D.1-6．【题文】已知对数函数()()0,1xf a a ax >≠=，且其图象过点()3,27，()f x 的反函数记为()y g x =，则()g x 的解析式是 ( )A ．()3log g x x =B ．()2log g x x =C ．()13log g x x = D ．()12log g xx =7．【题文】若log 2log 20a b <<，则 ( )A ．01a b <<<B ．01b a <<<C ．1a b >>D ．1b a >>8.【题文】当()1,2x ∈时，不等式()21log a x x <－恒成立，则实数a 的取值范围是( ) A ．()0,1 B ．()1,2 C ．(]1,2 D ．10,2⎛⎫ ⎪⎝⎭二、填空题（本题共3个小题）9.【题文】已知函数()log 21a y x =--的图象恒过定点P ，则点P 的坐标是________． 10．【题文】若指数函数()()x f x a x =∈R 的部分对应值如下表：则不等式()log 10a x ->的解集为______________． 11．【题文】已知()()1,53,log ,1a f x a x a x x x <⎧--=⎨≥⎩是(),-∞+∞上的增函数，则a 的取值范围为______．三、解答题（本题共3个小题）12.【题文】求下列函数的定义域与值域： (1)()2log 1y x =-； (2)()24log 4y x =+． 13.【题文】(1)已知1log 12a>，求a 的取值范围； (2)已知()()lg 21lg 31x x +>-，求x 的取值范围． 14．【题文】已知函数()121log 1f x x ax-=-的图象关于原点对称，其中a 为常数． (1)求实数a 的值；(2)若当()1,x ∈∞+时，()()12log 1f x x m +-<恒成立．求实数m 的取值范围．2.2.2对数函数及其性质（A 卷）参考答案及解析 1. 【答案】D【解析】由题意得12a -=，故3a =. 考点：由函数值求自变量值. 【题型】选择题 【难度】较易 2. 【答案】A【解析】自变量x 满足1210,.2x x ->∴>故选A. 考点：对数函数的定义域.【题型】选择题 【难度】一般 3. 【答案】 B【解析】因为对数函数的真数只能含自变量x ，所以(1)、(2)都不符合；(3)符合对数函数的定义，所以只有(3)是对数函数，故选B. 考点：对数函数的定义. 【题型】选择题 【难度】较易 4. 【答案】C【解析】∵322x+>，∴()()22log 32log 21x f x =+>=，∴()f x 的值域为()1,+∞.考点：对数函数的值域. 【题型】选择题 【难度】一般 5. 【答案】D【解析】由21log 2a =，解得a ；由122a=，解得1a =-，故选D. 考点：对数函数和指数函数的定义. 【题型】选择题 【难度】一般 6. 【答案】A【解析】由题意得327a =，∴3a =.因此()3xf x =，所以()f x 的反函数为()3log g x x =.考点：反函数、指对互化. 【题型】选择题 【难度】一般 7. 【答案】B【解析】由底数与对数函数的图象关系可知log a y x =，log b y x =的大致图象如图所示．对数函数的图象规律：从第一象限看，自左向右底数依次增大．故选B. 考点：对数函数单调性. 【题型】选择题 【难度】一般 8. 【答案】 C【解析】 设()()211f x x =－，()2log a f x x =，要使当()1,2x ∈时，不等式()21log a x x <－恒成立，只需()()211f x x =－在()1,2上的图象在()2log a f x x =的图象下方即可． 当01a <<时，由图象知显然不成立． 当1a >时，如图所示，要使当()1,2x ∈时，()()211f x x =－的图象在()2log a f x x =的图象下方，只需()()1222f f ≤，即()221log 2a ≤－，log 21a ≥， ∴12a <≤.故选C.考点：图象法求参数. 【题型】选择题 【难度】较难 9. 【答案】()3,1-【解析】log a y x =的图象恒过点()1,0，令21x -=，则3x =； 令10y +=，则1y =-.所以P 的坐标是()3,1-. 考点：对数函数图象恒过定点. 【题型】填空题 【难度】较易10. 【答案】{}2|1x x <<【解析】由题可知0.5a =，∴原不等式为()0.5log 10x ->， ∴()0.50.5log 1log 1x ->，解得2x <， 又∵10x ->，即1x >，∴12x <<. 故原不等式的解集为{}2|1x x <<． 考点：对数函数性质. 【题型】填空题 【难度】一般 11. 【答案】5,54⎡⎫⎪⎢⎣⎭【解析】()f x 是R 上的增函数，则当1x ≥时，log a y x =是增函数，∴1a >；当1x <时，函数()53y a x a =--是增函数，∴50a ->，∴5a <. 由()513log 1a a a -⨯-≤，得54a ≥. ∴545a ≤<. 考点：分段函数的单调性. 【题型】填空题 【难度】一般12. 【答案】(1)定义域是()1,+∞，值域是R (2)定义域是R ，值域是[)1,+∞【解析】(1)由10x ->，得1x >，所以函数()2log 1y x =-的定义域是()1,+∞.值域是R . (2)因为对任意实数x ，()24log 4x +都有意义， 所以函数()24log 4y x =+的定义域是R .又因为244x +≥，所以()244log 4log 41x ≥=+， 即函数()24log 4y x =+的值域是[)1,+∞． 考点：对数型函数的定义域与值域. 【题型】解答题 【难度】一般 13. 【答案】(1)1,12⎛⎫⎪⎝⎭(2)1,23⎛⎫⎪⎝⎭【解析】(1)由1log 12a>得1log 2log a a a >.①当1a >时，有12a <，此时无解； ②当01a <<时，有12a <，从而121a <<. ∴a 的取值范围是1,12⎛⎫⎪⎝⎭． (2)∵函数lg y x =在()0,+∞上为增函数，∴由()()lg 21lg 31x x +>-得210,310,2131,x x x x +>⎧⎪->⎨⎪+>-⎩解得123x <<.∴x 的取值范围为1,23⎛⎫ ⎪⎝⎭． 考点：对数函数的性质. 【题型】解答题 【难度】一般14. 【答案】(1)1a =- (2)1m ≥- 【解析】(1)∵函数()f x 的图象关于原点对称， ∴函数()f x 为奇函数， ∴()()f x f x -=-， 即111222111log log log 111ax ax x x x ax+--=-=----， 解得1a =-或1a =(舍)． (2)()()()()111122221log 1log log 1log 11xx x x x f x ++-=+-=+-， 当1x >时，()12log 11x +<-，∵当()1,x ∈∞+时，()()12log 1f x x m +-<恒成立，∴1m ≥-.考点：由奇函数及不等式恒成立求参数范围. 【题型】解答题 【难度】较难。

2.2.2　对数函数及其性质课后篇巩固提升基础巩固1.y=2x与y=log2x的图象关于( )A.x轴对称B.直线y=x对称C.原点对称D.y轴对称y=2x与y=log2x互为反函数,故函数图象关于直线y=x对称.2.函数y=ln(1-x)的图象大致为( )(-∞,1),且函数在定义域上单调递减,故选C.3.已知函数y=log a(x+c)(a,c为常数,且a>0,a≠1)的图象如图所示,则下列结论成立的是( )A.a>1,c>1B.a>1,0<c<1C.0<a<1,c>1D.0<a<1,0<c<1y=log a (x+c )的图象是由y=log a x 的图象向左平移c 个单位长度得到的,结合题图知0<c<1.根据单调性易知0<a<1.4.已知a>0且a ≠1,函数y=log a x ,y=a x ,y=x+a 在同一坐标系中的图象可能是( )函数y=a x 与y=log a x 的图象关于直线y=x 对称,再由函数y=a x 的图象过(0,1),y=log a x 的图象过(1,0),观察图象知,只有C 正确.5.已知a=,b=log 2,c=lo ,则( )2-1313g 1213A.a>b>cB.a>c>bC.c>b>aD.c>a>b0<a=<20=1,b=log 2<log 21=0,c=lo >lo =1,∴c>a>b.故选D .2-1313g 1213g 12126.若对数函数f (x )的图象经过点P (8,3),则f = .(12)f (x )=log a x (a>0,a ≠1),则log a 8=3,∴a 3=8,∴a=2.∴f (x )=log 2x ,故f =log 2=-1.(12)1217.将y=2x 的图象先 ,再作关于直线y=x 对称的图象,可得到函数y=log 2(x+1)的图象( )A.先向上平移一个单位长度B.先向右平移一个单位长度C.先向左平移一个单位长度D.先向下平移一个单位长度,可求出解析式或利用几何图形直观推断.8.已知函数f (x )=直线y=a 与函数f (x )的图象恒有两个不同的交点,则a 的取值范围{log 2x ,x >0,3x ,x ≤0,是 .f (x )的图象如图所示,要使直线y=a 与f (x )的图象有两个不同的交点,则0<a ≤1.9.作出函数y=|log 2x|+2的图象,并根据图象写出函数的单调区间及值域.y=log 2x 的图象,如图甲.再将y=log 2x 在x 轴下方的图象关于x 轴对称翻折到x 轴上方(原来在x 轴上方的图象不变),得函数y=|log 2x|的图象,如图乙;然后将y=|log 2x|的图象向上平移2个单位长度,得函数y=|log 2x|+2的图象,如图丙.由图丙得函数y=|log 2x|+2的单调递增区间是[1,+∞),单调递减区间是(0,1),值域是[2,+∞).10.已知对数函数y=f(x)的图象经过点P(9,2).(1)求y=f(x)的解析式;(2)若x∈(0,1),求f(x)的取值范围.(3)若函数y=g(x)的图象与函数y=f(x)的图象关于x轴对称,求y=g(x)的解析式.设f(x)=log a x(a>0,且a≠1).由题意,f(9)=log a9=2,故a2=9,解得a=3或a=-3.又因为a>0,所以a=3.故f(x)=log3x.(2)因为3>1,所以当x∈(0,1)时,f(x)<0,即f(x)的取值范围为(-∞,0).g1(3)因为函数y=g(x)的图象与函数y=log3x的图象关于x轴对称,所以g(x)=lo x.3能力提升1.函数y=log a(x+2)+1(a>0,且a≠1)的图象过定点( )A.(1,2)B.(2,1)C.(-2,1)D.(-1,1)x+2=1,得x=-1,此时y=1.2.若函数f (x )=log 2x 的反函数为y=g (x ),且g (a )=,则a=( )14A.2 B.-2 C. D.-1212,得g (x )=2x .∵g (a )=,∴2a =,∴a=-2.14143.若函数f (x )=log 2(x 2-ax-3a )在区间(-∞,-2]上是减函数,则实数a 的取值范围是( )A.(-∞,4)B.(-4,4]C.(-∞,4)∪[2,+∞)D.[-4,4)t (x )=x 2-ax-3a ,则由函数f (x )=log 2t 在区间(-∞,-2]上是减函数,可得函数t (x )在区间(-∞,-2]上是减函数,且t (-2)>0,所以有-4≤a<4,故选D .4.已知函数f (x )=a x +log a (x+1)在[0,1]上的最大值与最小值之和为a ,则a 的值等于( )A. B.2 C.3D.1213y=a x 与y=log a (x+1)在[0,1]上的单调性相同,所以f (x )在[0,1]上的最大值与最小值之和为f (0)+f (1)=(a 0+log a 1)+(a 1+log a 2)=a ,整理得1+a+log a 2=a ,即log a 2=-1,解得a=.故选A .125.已知a=log 23.6,b=log 43.2,c=log 43.6,则a ,b ,c 的大小关系为 .a==2log 43.6=log 43.62,又函数y=log 4x 在区间(0,+∞)上是增函数,3.62>3.6>3.2,log 43.6log 42∴log 43.62>log 43.6>log 43.2,∴a>c>b.6.已知a>0且a ≠1,则函数y=a x 与y=log a (-x )在同一直角坐标系中的图象只能是下图中的 (填序号).方法一)首先,曲线y=a x 位于x 轴上方,y=log a (-x )位于y 轴左侧,从而排除①③.其次,从单调性考虑,y=a x 与y=log a (-x )的增减性正好相反,又可排除④.故只有②满足条件.(方法二)若0<a<1,则曲线y=a x 下降且过点(0,1),而曲线y=log a (-x )上升且过点(-1,0),所有选项均不符合这些条件.若a>1,则曲线y=a x 上升且过点(0,1),而曲线y=log a (-x )下降且过点(-1,0),只有②满足条件.(方法三)如果注意到y=log a (-x )的图象关于y 轴的对称图象为y=log a x 的图象,又y=log a x 与y=a x 互为反函数(两者图象关于直线y=x 对称),则可直接选②.7.已知函数f (x )是定义在R 上的奇函数,若当x ∈(0,+∞)时,f (x )=lg x ,则满足f (x )>0的x 的取值范围是 .f (x )的解析式为f (x )=其图象如右图所示.{lg x ,x >0,0,x =0,-lg (-x ),x <0,由函数图象可得不等式f (x )>0时,x 的取值范围为(-1,0)∪(1,+∞).-1,0)∪(1,+∞)8.设函数f (x )=ln(ax 2+2x+a )的定义域为M.(1)若1∉M ,2∈M ,求实数a 的取值范围;(2)若M=R ,求实数a 的取值范围.由题意M={x|ax 2+2x+a>0}.由1∉M ,2∈M 可得{a ×12+2×1+a ≤0,a ×22+2×2+a >0,化简得解得-<a ≤-1.{2a +2≤0,5a +4>0,45所以a 的取值范围为.(-45,-1](2)由M=R 可得ax 2+2x+a>0恒成立.当a=0时,不等式可化为2x>0,解得x>0,显然不合题意;当a ≠0时,由二次函数的图象可知Δ=22-4×a×a<0,且a>0,即化简得解得a>1.{4-4a 2<0,a >0,{a 2>1,a >0,所以a 的取值范围为(1,+∞).9.已知函数f (x )=log 2(a 为常数)是奇函数.1+ax x -1(1)求a 的值与函数f (x )的定义域;(2)若当x ∈(1,+∞)时,f (x )+log 2(x-1)>m 恒成立,求实数m 的取值范围.∵函数f (x )=log 2是奇函数,1+axx -1∴f (-x )=-f (x ).∴log 2=-log 2.1-ax -x -11+ax x -1即log 2=log 2,∴a=1.ax -1x +1x -11+ax 令>0,解得x<-1或x>1.1+x x -1所以函数的定义域为{x|x<-1或x>1}.(2)f (x )+log 2(x-1)=log 2(1+x ),当x>1时,x+1>2,∴log 2(1+x )>log 22=1.∵x ∈(1,+∞),f (x )+log 2(x-1)>m 恒成立,∴m ≤1.故m 的取值范围是(-∞,1].。

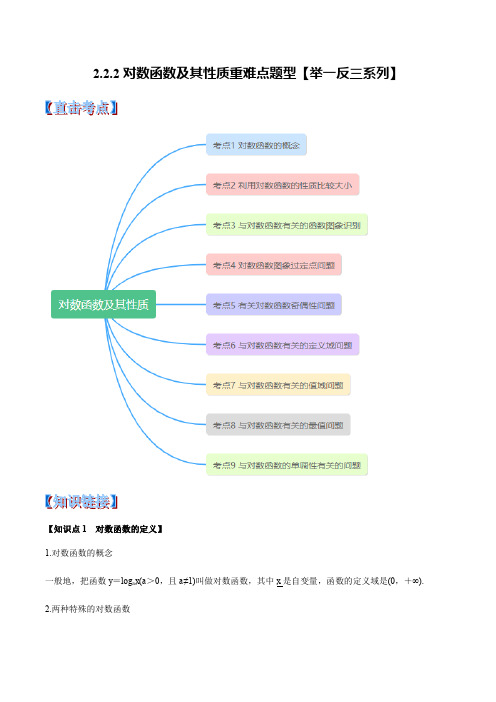
2.2.2对数函数及其性质重难点题型【举一反三系列】【知识点1 对数函数的定义】1.对数函数的概念一般地，把函数y＝log a x(a＞0，且a≠1)叫做对数函数，其中x是自变量，函数的定义域是(0，＋∞).2.两种特殊的对数函数（1）常用对数函数：以10为底的对数函数x y lg =. （2）自然对数函数：以无理数e 为底的对数函数x y ln =. 【知识点2 对数函数的图象与性质】 对数函数的图象与性质列表如下：温馨提示：掌握对数函数的图象和性质，其关键是理解图象的特征，利用几何直观掌握函数的性质. 【知识点3 反函数】在指数函数)10(≠>=a a a y x ，中，x 是自变量，y 是x 的函数，其定义域是R ，值域是（0，+∞）；在对数函数)1,0(log ≠>=a a y x a 中，y 是自变量，x 是y 的函数，其定义域是R ，值域是（0，+∞）， 像这样的两个函数叫作互为反函数.【考点1 对数函数的概念】【例1】（2019秋•林芝县校级月考）下列函数是对数函数的是（）A．y＝log3（x+1）B．y＝log a（2x）（a＞0，且a≠1）C．y＝lnxD．【变式1-1】给出下列函数：①y＝x2；②y＝log3（x﹣1）；③y＝log x+1x；④y＝logπx．其中是对数函数的有（）A．1个B．2个C．3个D．4个【变式1-2】下列函数表达式中，是对数函数的有（）①y＝log x2；②y＝log a x（a∈R）③y＝log8x；④y＝lnx⑤y＝log x（x+2）；⑥y＝2log4x⑦y＝log2（x+1）A．1个B．2个C．3个D．4个【变式1-3】下列函数中，是对数函数的个数为（）①y＝log a x2（a＞0，且a≠1）；②y＝log2x﹣1；③y＝2log8x；④y＝log x a（x＞0，且x≠1）；⑤y＝log5x；⑥y＝log a x（a＞0，a≠1）A．1B．2C．3D．4【考点2 利用对数函数的性质比较大小】【例2】（2019秋•福田区校级月考）设，则a，b，c的大小关系是（）A．a＜b＜c B．b＜c＜a C．a＜c＜b D．c＜b＜a【变式2-1】（2019秋•天山区校级月考）已知正实数a，b，c满足log a2＝2，log3b＝，c6＝7，则a，b，c的大小关系是（）A．a＜b＜c B．a＜c＜b C．c＜b＜a D．c＜a＜b【变式2-2】（2019秋•沙坪坝区校级月考）已知a＝log30.3，b＝30.3，c＝0.30.2，则（）A．a＜b＜c B．a＜c＜b C．c＜a＜b D．b＜c＜a【变式2-3】（2019•西湖区校级模拟）下列关系式中，成立的是（）A．B．C．D．【考点3 与对数函数有关的函数图象识别】【例3】（2018秋•合阳县期末）已知a＞0，b＞0，且ab＝1，a≠1，则函数f（x）＝a x与函数g（x）＝﹣log b x在同一坐标系中的图象可能是（）A．B．C．D．【变式3-1】（2019•西湖区校级模拟）若当x∈R时，函数f（x）＝a|x|始终满足0＜|f（x）|≤1，则函数y＝log a||的图象大致为（）A．B．C．D．【变式3-2】（2018秋•船营区校级月考）函数f（x）＝的图象可能是（）A．B．C．D．【变式3-3】（2019秋•洛南县期末）函数y＝|lg（x+1）|的图象是（）A．B．C．D．【考点4 对数函数图象过定点问题】【例4】（2018秋•赣州期中）函数y＝log a（x﹣1）+log a（x+1）（a＞0且a≠1）的图象必过定点（）A．（）B．（0，﹣）C．（）D．（）【变式4-1】（2019秋•水富县校级月考）已知函数y＝3+log a（2x+3）（a＞0，a≠1）的图象必经过定点P，则P点坐标是（）A．（1，3）B．（﹣，4）C．（﹣1，3）D．（﹣1，4）【变式4-2】（2018秋•烟台期中）函数y＝log a（x+2）+a x+1+2（a＞0，且a≠1）的图象必经过的点是（）A．（0，2）B．（2，2）C．（﹣1，2）D．（﹣1，3）【变式4-3】（2019秋•赣州期末）已知a＞0，a≠1，则f（x）＝log a的图象恒过点（）A．（1，0）B．（﹣2，0）C．（﹣1，0）D．（1，4）【考点5 有关对数函数奇偶性问题】【例5】（2018•肇庆二模）已知f（x）＝lg（10+x）+lg（10﹣x），则f（x）是（）A．f（x）是奇函数，且在（0，10）是增函数B．f（x）是偶函数，且在（0，10）是增函数C．f（x）是奇函数，且在（0，10）是减函数D．f（x）是偶函数，且在（0，10）是减函数【变式5-1】（2019秋•南充期末）已知函数f（x）＝log a（x﹣m）的图象过点（4，0）和（7，1），则f （x）在定义域上是（）A．增函数B．减函数C．奇函数D．偶函数【变式5-2】（2019秋•新宁县校级期中）对于函数，下列说法正确的是（）A．f（x）是奇函数B．f（x）是偶函数C．f（x）是非奇非偶函数D．f（x）既是奇函数又是偶函数【变式5-3】（2016春•石家庄校级月考）函数f（x）＝ln（1+2x），g（x）＝ln（1﹣2x），则f（x）+g（x）为（）A．奇函数B．偶函数C．既不是奇函数又不是偶函数D．既是奇函数又是偶函数【考点6 与对数函数有关的定义域问题】【例6】（2018秋•肇庆期末）函数y＝的定义域为（）A．（1，+∞）B．[1，+∞）C．（1，2）∪（2，+∞）D．（1，2）∪[3，+∞）【变式6-1】（2019•西湖区校级模拟）函数的定义域是（）A．B．C．D．【变式6-2】（2018秋•宜宾期末）函数y＝的定义域是（）A．（，+∞）B．（，1]C．（﹣∞，1]D．[1，+∞）【变式6-3】（2018春•连城县校级月考）函数y＝的定义域是（）A．[1，+∞）B．（，+∞）C．（1，+∞）D．（，1]【考点7 与对数函数有关的值域问题】【例7】（2019秋•南昌校级期中）函数y＝log4（2x+3﹣x2）值域为．【变式7-1】（2019春•赣榆区校级月考）函数的值域为．【变式7-2】（2019秋•九原区校级期末）函数y＝（x）2﹣x2+5 在2≤x≤4时的值域为．【变式7-3】（2019秋•松江区期末）函数的值域为．【考点8 与对数函数有关的最值问题】【例8】（2019秋•离石区校级月考）设x≥0，y≥0且x+2y＝，则函数u＝log0.5（8xy+4y2+1）的最大值为．【变式8-1】（2019秋•田阳县校级月考）函数f（x）＝log a（x+1）在[0，3]上的最大值与最小值的差为2，则a的值为．【变式8-2】（2019春•天津期末）若函数y＝log a（x2﹣ax+1）有最小值，则a的取值范围是．【变式8-3】（2019秋•会宁县校级期中）已知函数f（x）＝2+log3x，x∈[1，9]，函数y＝[f（x）]2+f（x2）的最大值为．【考点9 与对数函数的单调性有关的问题】【例9】（2019春•吉林期末）已知函数f（x）＝log a（x+3）﹣log a（3﹣x），a＞0且a≠1．（1）求函数f（x）的定义域；（2）判断并证明函数f（x）的奇偶性；（3）若a＞1，指出函数的单调性，并求函数f（x）在区间[0，1]上的最大值．【变式9-1】（2018秋•南岗区校级期中）已知f（x）＝log a（a＞0，且a≠1，m≠﹣1）是定义在区间（﹣1，1）上的奇函数，（1）求f（0）的值和实数m的值；（2）判断函数f（x）在区间（﹣1，1）上的单调性，并说明理由；（3）若f（）＞0且f（b﹣2）+f（2b﹣2）＞0成立，求实数b的取值范围．【变式9-2】（2019秋•番禺区校级期中）已知函数．（1）求函数的定义域．（2）讨论函数f（x）的奇偶性．（3）判断函数f（x）的单调性，并用定义证明．【变式9-3】（2019秋•荔湾区校级期末）已知函数f（x）＝log3（1+x）﹣log3（1﹣x）．（1）求函数f（x）定义域，并判断f（x）的奇偶性．（2）判断函数f（x）在定义域内的单调性，并用单调性定义证明你的结论．（3）解关于x的不等式f（1﹣x）+f（1﹣x2）＞0．2.2.2对数函数及其性质重难点题型【举一反三系列】【知识点1 对数函数的定义】 1.对数函数的概念一般地，把函数y ＝log a x (a ＞0，且a ≠1)叫做对数函数，其中x 是自变量，函数的定义域是(0，＋∞). 2.两种特殊的对数函数（1）常用对数函数：以10为底的对数函数x y lg =. （2）自然对数函数：以无理数e 为底的对数函数x y ln =. 【知识点2 对数函数的图象与性质】对数函数的图象与性质列表如下：温馨提示：掌握对数函数的图象和性质，其关键是理解图象的特征，利用几何直观掌握函数的性质. 【知识点3 反函数】在指数函数)10(≠>=a a a y x ，中，x 是自变量，y 是x 的函数，其定义域是R ，值域是（0，+∞）；在对数函数)1,0(log ≠>=a a y x a 中，y 是自变量，x 是y 的函数，其定义域是R ，值域是（0，+∞）， 像这样的两个函数叫作互为反函数.【考点1 对数函数的概念】【例1】（2019秋•林芝县校级月考）下列函数是对数函数的是（ ） A ．y ＝log 3（x +1）B．y＝log a（2x）（a＞0，且a≠1）C．y＝lnxD．【分析】根据对数函数的定义即可得出．【答案】解：根据对数函数的定义可得：只有y＝lnx为对数函数．故选：C．【点睛】本题考查了对数函数的定义，考查了推理能力与计算能力，属于基础题．【变式1-1】给出下列函数：①y＝x2；②y＝log3（x﹣1）；③y＝log x+1x；④y＝logπx．其中是对数函数的有（）A．1个B．2个C．3个D．4个【分析】由对数函数的定义依次判断即可．【答案】解：①y＝x2的真数为x2，故不是对数函数；②y＝log3（x﹣1）的真数为x﹣1，故不是对数函数；③y＝log x+1x的底数为x+1，故不是对数函数；④y＝logπx是对数函数；故选：A．【点睛】本题考查了对数函数的定义的应用．【变式1-2】下列函数表达式中，是对数函数的有（）①y＝log x2；②y＝log a x（a∈R）③y＝log8x；④y＝lnx⑤y＝log x（x+2）；⑥y＝2log4x⑦y＝log2（x+1）A．1个B．2个C．3个D．4个【分析】根据对数函数的定义，y＝log a x（a＞0，且a≠1），逐一分析给定函数是否为指数函数，可得结论．【答案】解：①y＝log x2不是对数函数；②y＝log a x（a∈R）不是对数函数；③y＝log8x是对数函数；④y＝lnx是对数函数；⑤y＝log x（x+2）不是对数函数；⑥y＝2log4x不是对数函数；⑦y＝log2（x+1）不是对数函数；综上所述，对数函数有2个，故选：B．【点睛】本题考查的知识点是对数函数的定义，熟练掌握对数函数的定义，是解答的关键．【变式1-3】下列函数中，是对数函数的个数为（）①y＝log a x2（a＞0，且a≠1）；②y＝log2x﹣1；③y＝2log8x；④y＝log x a（x＞0，且x≠1）；⑤y＝log5x；⑥y＝log a x（a＞0，a≠1）A．1B．2C．3D．4【分析】根据对数函数的定义进行判断即可．【答案】解：①y＝log a x2（a＞0，且a≠1），真数不是变量x，不是对数函数；②y＝log2x﹣1，不是对数函数；③y＝2log8x；系数不是1，不是对数函数④y＝log x a（x＞0，且x≠1），底数不是常数，不是对数函数；⑤y＝log5x，满足对数函数的定义，是对数函数；⑥y＝log a x（a＞0，a≠1）满足对数函数的定义，是对数函数，故是对数函数的有⑤⑥，共有2个，故选：B．【点睛】本题主要考查函数概念的判断，根据对数函数的定义是解决本题的关键．【考点2 利用对数函数的性质比较大小】【例2】（2019秋•福田区校级月考）设，则a，b，c的大小关系是（）A．a＜b＜c B．b＜c＜a C．a＜c＜b D．c＜b＜a【分析】根据对数的换底公式可得出，从而可得出2＜log420＜log315，且可得出，这样即可得出a，b，c的大小关系．【答案】解：，，，且log54＞log53＞0，∴，∴2＝log416＜log420＜log315，∴a＜c＜b．故选：C．【点睛】考查对数的换底公式，以及指数函数和对数函数的单调性，增函数的定义，不等式的性质．【变式2-1】（2019秋•天山区校级月考）已知正实数a，b，c满足log a2＝2，log3b＝，c6＝7，则a，b，c的大小关系是（）A．a＜b＜c B．a＜c＜b C．c＜b＜a D．c＜a＜b【分析】根据条件可得出，从而得出a6＝8，b6＝9且c6＝7，a，b，c都是正数，这样即可得出a，b，c的大小关系．【答案】解：∵log a2＝2，log3b＝，c6＝7，∴∴a6＝8，b6＝9，c6＝7，且a，b，c都是正数，∴c＜a＜b故选：C．【点睛】考查对数的定义，对数与指数的互化，以及指数的运算，幂函数的单调性．【变式2-2】（2019秋•沙坪坝区校级月考）已知a＝log30.3，b＝30.3，c＝0.30.2，则（）A．a＜b＜c B．a＜c＜b C．c＜a＜b D．b＜c＜a【分析】容易得出，从而可得出a，b，c的大小关系．【答案】解：∵log30.3＜log31＝0，30.3＞30＝1，0＜0.30.2＜0.30＝1∴a＜c＜b．故选：B．【点睛】考查对数函数、指数函数的单调性，以及增函数、减函数的定义．【变式2-3】（2019•西湖区校级模拟）下列关系式中，成立的是（）A．B．C．D．【分析】容易得出，从而可得出正确的选项．【答案】解：∵log34＞log33＝1，0＜0.31.7＜0.30＝1，log0.310＜log0.31＝0，∴．故选：A．【点睛】考查对数函数和指数函数的单调性，增函数和减函数的定义．【考点3 与对数函数有关的函数图象识别】【例3】（2018秋•合阳县期末）已知a＞0，b＞0，且ab＝1，a≠1，则函数f（x）＝a x与函数g（x）＝﹣log b x在同一坐标系中的图象可能是（）A．B．C．D．【分析】根据a与b的正负，利用指数函数与对数函数的性质判断即可确定出其图象．【答案】解：∵a＞0，b＞0，且ab＝1，a≠1，∴函数f（x）＝a x与函数g（x）＝﹣log b x在同一坐标系中的图象可能是，故选：B．【点睛】此题考查了指数函数与对数函数的图象，熟练掌握指数、对数函数的图象与性质是解本题的关键．【变式3-1】（2019•西湖区校级模拟）若当x∈R时，函数f（x）＝a|x|始终满足0＜|f（x）|≤1，则函数y＝log a||的图象大致为（）A．B．C．D．【分析】由于当x∈R时，函数f（x）＝a|x|始终满足0＜|f（x）|≤1，利用指数函数的图象和性质可得0＜a＜1．先画出函数y＝log a|x|的图象，此函数是偶函数，当x＞0时，即为y＝log a x，而函数y＝log a||＝﹣log a|x|，即可得出图象．【答案】解：∵当x∈R时，函数f（x）＝a|x|始终满足0＜|f（x）|≤1．因此，必有0＜a＜1．先画出函数y＝log a|x|的图象：红颜色的图象．而函数y＝log a||＝﹣log a|x|，其图象如黑颜色的图象．故选：B．【变式3-2】（2018秋•船营区校级月考）函数f（x）＝的图象可能是（）A．B．C．D．【分析】先求出函数的定义域，再判断函数为奇函数，即图象关于原点对称，故可以排除BC，再根据函数值域，可排除D．【答案】解：∵f（x）＝，∴函数定义域为（﹣∞，0）∪（0，+∞），∵，∴函数f（x）为奇函数，图象关于原点对称，故排除B、C，∵当0＜x＜1时，lnx＜0，∴f（x）＝＜0，x∈（0，1）故排除D．故选：A．【点睛】本题主要考查了绝对值函数以及函数的值域、奇偶性和单调性，属于基础题．【变式3-3】（2019秋•洛南县期末）函数y＝|lg（x+1）|的图象是（）A．B．C．D．【分析】本题研究一个对数型函数的图象特征，函数y＝|lg（x+1）|的图象可由函数y＝lg（x+1）的图象将X轴下方的部分翻折到X轴上部而得到，故首先要研究清楚函数y＝lg（x+1）的图象，由图象特征选出正确选项【答案】解：由于函数y＝lg（x+1）的图象可由函数y＝lgx的图象左移一个单位而得到，函数y＝lgx的图象与X轴的交点是（1，0），故函数y＝lg（x+1）的图象与X轴的交点是（0，0），即函数y＝|lg（x+1）|的图象与X轴的公共点是（0，0），考察四个选项中的图象只有A选项符合题意故选：A．【点睛】本题考查对数函数的图象与性质，解答本题关键是掌握住对数型函数的图象图象的变化规律，由这些规律得出函数y＝|lg（x+1）|的图象的特征，再由这些特征判断出函数图象应该是四个选项中的那一个【考点4 对数函数图象过定点问题】【例4】（2018秋•赣州期中）函数y＝log a（x﹣1）+log a（x+1）（a＞0且a≠1）的图象必过定点（）A．（）B．（0，﹣）C．（）D．（）【分析】根据对数函数的性质求出定点的坐标即可．【答案】解：y＝log a（x﹣1）+log a（x+1）＝log a（x2﹣1），令x2﹣1＝1，解得：x＝±，而x﹣1＞0，解得：x＞1，故x＝，故函数的图象过（，0），故选：C．【点睛】本题考查了对数函数的性质，考查特殊值问题，是一道基础题．【变式4-1】（2019秋•水富县校级月考）已知函数y＝3+log a（2x+3）（a＞0，a≠1）的图象必经过定点P，则P点坐标是（）A．（1，3）B．（﹣，4）C．（﹣1，3）D．（﹣1，4）【分析】令2x+3＝1，求得x的值，从而求得P点的坐标．【答案】解：令2x+3＝1，可得x＝﹣1，此时y＝3．即函数y＝3+log a（2x+3）（a＞0，a≠1））的图象必经过定点P的坐标为（﹣1，3）．故选：C．【点睛】本题主要考查对数函数的单调性和特殊点，属于基础题．【变式4-2】（2018秋•烟台期中）函数y＝log a（x+2）+a x+1+2（a＞0，且a≠1）的图象必经过的点是（）A．（0，2）B．（2，2）C．（﹣1，2）D．（﹣1，3）【分析】根据log a1＝0，a0＝1，求出定点的坐标即可．【答案】解：令x+2＝1，解得：x＝﹣1，故y＝0+1+2＝3，故图象过（﹣1，3），故选：D．【点睛】本题考查了对数函数，指数函数的性质，根据log a1＝0，a0＝1是解题的关键．【变式4-3】（2019秋•赣州期末）已知a＞0，a≠1，则f（x）＝log a的图象恒过点（）A．（1，0）B．（﹣2，0）C．（﹣1，0）D．（1，4）【分析】令＝1，解得x＝﹣2，y＝0，进而得到f（x）＝log a的图象恒过点的坐标．【答案】解：令＝1，解得：x＝﹣2，故f（﹣2）＝log a1＝0恒成立，即f（x）＝log a的图象恒过点（﹣2，0），故选：B．【点睛】本题考查的知识点是对数函数的图象和性质，熟练掌握对数函数的图象和性质，是解答的关键．【考点5 有关对数函数奇偶性问题】【例5】（2018•肇庆二模）已知f（x）＝lg（10+x）+lg（10﹣x），则f（x）是（）A．f（x）是奇函数，且在（0，10）是增函数B．f（x）是偶函数，且在（0，10）是增函数C．f（x）是奇函数，且在（0，10）是减函数D．f（x）是偶函数，且在（0，10）是减函数【分析】求出函数的定义域，根据函数奇偶性的定义以及复合函数的单调性判断即可．【答案】解：由得：x∈（﹣10，10），故函数f（x）的定义域为（﹣10，10），关于原点对称，又由f（﹣x）＝lg（10﹣x）+lg（10+x）＝f（x），故函数f（x）为偶函数，而f（x）＝lg（10+x）+lg（10﹣x）＝lg（100﹣x2），y＝100﹣x2在（0，10）递减，y＝lgx在（0，10）递增，故函数f（x）在（0，10）递减，故选：D．【点睛】本题考查了函数的单调性和函数的奇偶性问题，考查转化思想，是一道基础题．【变式5-1】（2019秋•南充期末）已知函数f（x）＝log a（x﹣m）的图象过点（4，0）和（7，1），则f （x）在定义域上是（）A．增函数B．减函数C．奇函数D．偶函数【分析】把（4，0）和（7，1）代入f（x）列出方程组解出a，m，根据对数函数的性质判断．【答案】解：∵f（x）的图象过点（4，0）和（7，1），∴，解得．∴f（x）＝log4（x﹣3）．∴f（x）是增函数．∵f（x）的定义域是（3，+∞），不关于原点对称．∴f（x）为非奇非偶函数．故选：A．【点睛】本题考查了对数函数的性质，属于基础题．【变式5-2】（2019秋•新宁县校级期中）对于函数，下列说法正确的是（）A．f（x）是奇函数B．f（x）是偶函数C．f（x）是非奇非偶函数D．f（x）既是奇函数又是偶函数【分析】根据函数奇偶性的定义判断函数的奇偶性即可．【答案】解：由＞0，解得：﹣1＜x＜1，故函数f（x）的定义域是（﹣1，1），关于原点对称，而f（﹣x）＝log2＝﹣log2＝﹣f（x），故f（x）是奇函数，故选：A．【点睛】本题考查了函数的奇偶性问题，是一道基础题．【变式5-3】（2016春•石家庄校级月考）函数f（x）＝ln（1+2x），g（x）＝ln（1﹣2x），则f（x）+g（x）为（）A．奇函数B．偶函数C．既不是奇函数又不是偶函数D．既是奇函数又是偶函数【分析】首先令h（x）＝f（x）+g（x），求出h（x）的定义域，而后用函数奇偶性定义求证．【答案】解：令h（x）＝f（x）+g（x）＝ln（2x+1）+ln（1﹣2x）由得：﹣＜x＜，h（x）定义域为（﹣，），∴h（﹣x）＝ln（1﹣2x）+ln（1+2x）＝h（x），所以，h（x）为偶函数．故选：B．【点睛】本题主要考查了奇偶函数的定义域要求，以及函数奇偶性定义，属基础题．【考点6 与对数函数有关的定义域问题】【例6】（2018秋•肇庆期末）函数y＝的定义域为（）A．（1，+∞）B．[1，+∞）C．（1，2）∪（2，+∞）D．（1，2）∪[3，+∞）【分析】根据分式的分母不为0，对数的真数大于0，建立关系式，解之即可．【答案】解：要使函数有意义则解得x＞1且x≠2∴函数的定义域为（1，2）∪（2，+∞）故选：C．【点睛】本题考查函数定义域的求解，属基础题，做这类题目的关键是找对自变量的限制条件．【变式6-1】（2019•西湖区校级模拟）函数的定义域是（）A．B．C．D．【分析】由函数的解析式列出不等式进行求解即可．【答案】解：由题意得，，解得x＞，则函数的定义域是，故选：C．【点睛】本题考查了函数的定义域的求法，属于基础题．【变式6-2】（2018秋•宜宾期末）函数y＝的定义域是（）A．（，+∞）B．（，1]C．（﹣∞，1]D．[1，+∞）【分析】首先由根式有意义得到log0.5（4x﹣3）≥0，然后求解对数不等式得到原函数的定义域．【答案】解：要使原函数有意义，则log0.5（4x﹣3）≥0，即0＜4x﹣3≤1，解得．所以原函数的定义域为（]．故选：B．【点睛】本题考查了对数函数定义域，训练了对数不等式的解法，是基础的计算题．【变式6-3】（2018春•连城县校级月考）函数y＝的定义域是（）A．[1，+∞）B．（，+∞）C．（1，+∞）D．（，1]【分析】利用对数的性质求解．【答案】解：函数y＝的定义域满足：，解得．故选：D．【点睛】本题考查对数函数的定义域的求法，解题时要注意对数性质的灵活运用，是基础题．【考点7 与对数函数有关的值域问题】【例7】（2019秋•南昌校级期中）函数y＝log4（2x+3﹣x2）值域为．【分析】运用复合函数的单调性分析函数最值，再通过配方求得值域．【答案】解：设u（x）＝2x+3﹣x2＝﹣（x﹣1）2+4，当x＝1时，u（x）取得最大值4，∵函数y＝log4x为（0，+∞）上的增函数，∴当u（x）取得最大值时，原函数取得最大值，即y max＝log4u（x）max＝log44＝1，因此，函数y＝log4（2x+3﹣x2）的值域为（﹣∞，1]，故填：（﹣∞，1]．【点睛】本题主要考查了函数值域的求法，涉及对数函数的单调性，用到配方法和二次函数的性质，属于基础题．【变式7-1】（2019春•赣榆区校级月考）函数的值域为．【分析】先将原函数y＝log0.5（x2+x+）转化为两个基本函数令t＝x2+x+＝（x+）2+，y＝log0.5t 的，再用复合函数的单调性求解．【答案】解：令t＝x2+x+＝（x+）2+∈[，+∞]，∵函数y＝log0.5t的在定义域上是减函数，∴y∈（﹣∞，2]；故答案为（﹣∞，2]．【点睛】本题主要考查用复合函数的单调性来求函数的值域，本题关键是求出二次函数的值域，属于基础题．【变式7-2】（2019秋•九原区校级期末）函数y＝（x）2﹣x2+5 在2≤x≤4时的值域为．【分析】利用换元法，令t＝由2≤x≤4 可得﹣1≤t≤﹣，由题意可得y＝＝（t﹣1）2+4，又因为函数在[﹣1，﹣]单调递减，从而可求函数的值域．【答案】解：令t＝，因为2≤x≤4，所以﹣1≤t≤﹣，则y＝＝（t﹣1）2+4，又因为函数在[﹣1，﹣]单调递减，当t＝﹣是函数有最小值，当t＝﹣1时函数有最大值8；故答案为：{y|}【点睛】本题主要考查了对数的运算性质，换元法的应用，二次函数性质的应用及函数的单调性的应用，属于基础知识的简单综合试题．【变式7-3】（2019秋•松江区期末）函数的值域为．【分析】由函数的解析式可得，当x＜1时，f（x）＞；当x≥1时，f（x）≥0，综上可得f（x）的值域．【答案】解：由于函数，故当x＜1时，f（x）＝＞．当x≥1时，f（x）＝log2x≥log21＝0．综上可得，f（x）≥0，故函数的值域为[0，+∞），故答案为[0，+∞）．【点睛】本题主要考查求函数的值域，指数函数、对数函数的单调性的应用，体现了分类讨论的数学思想，属于中档题．【考点8 与对数函数有关的最值问题】【例8】（2019秋•离石区校级月考）设x≥0，y≥0且x+2y＝，则函数u＝log0.5（8xy+4y2+1）的最大值为．【分析】由已知中x≥0，y≥0且x+2y＝，可得y∈[0，]，8xy+4y2+1＝﹣12y2+8y+1，结合二次函数的图象和性质及对数函数的图象和性质，可得答案．【答案】解：∵x+2y＝，∴x＝﹣2y，由x≥0，y≥0，可得y∈[0，]，则8xy+4y2+1＝﹣12y2+8y+1，令t＝﹣12y2+8y+1，当y∈[0，]时，t∈[1，]，又由u＝log0.5t为减函数，故当t＝1时函数u＝log0.5（8xy+4y2+1）的最大值为0，故答案为：0．【点睛】本题考查的知识点是对数函数的值域和最值，其中熟练掌握对数函数的图象和性质是解答的关键．【变式8-1】（2019秋•田阳县校级月考）函数f（x）＝log a（x+1）在[0，3]上的最大值与最小值的差为2，则a的值为．【分析】对a分a＞1与0＜a＜1两类讨论，利用函数的单调性即可．【答案】解：若a＞1，f（x）＝log a（x+1）在[0，3]上单调递增，∴f（x）max＝log a4＝2log a2，f（x）min＝log a1＝0，∵f（x）max﹣f（x）min＝2，∴2log a2﹣0＝2，∴log a2＝1，故a＝2；若0＜a＜1，f（x）＝log a（x+1）在[0，3]上单调递减，同理可得a＝．故答案为：2或．【点睛】本题考查对数函数的单调性与最值，考查分类讨论思想，属于中档题．【变式8-2】（2019春•天津期末）若函数y＝log a（x2﹣ax+1）有最小值，则a的取值范围是．【分析】先根据复合函数的单调性确定函数g（x）＝x2﹣ax+1的单调性，进而分a＞1和0＜a＜1两种情况讨论：①当a＞1时，考虑对数函数的图象与性质得到x2﹣ax+1的函数值恒为正；②当0＜a＜1时，△＝a2﹣4＜0恒成立，x2﹣ax+1没有最大值，从而不能使得函数y＝log a（x2﹣ax+1）有最小值．最后取这两种情形的并集即可．【答案】解：令g（x）＝x2﹣ax+1（a＞0，且a≠1），①当a＞1时，y＝log a x在R+上单调递增，∴要使y＝log a（x2﹣ax+1）有最小值，必须g（x）min＞0，∴△＜0，解得﹣2＜a＜2∴1＜a＜2；②当0＜a＜1时，g（x）＝x2﹣ax+1没有最大值，从而不能使得函数y＝log a（x2﹣ax+1）有最小值，不符合题意．综上所述：1＜a＜2；故答案为：1＜a＜2．【点睛】本题考查对数函数的值域最值，着重考查复合函数的单调性，突出分类讨论与转化思想的考查，是中档题．【变式8-3】（2019秋•会宁县校级期中）已知函数f（x）＝2+log3x，x∈[1，9]，函数y＝[f（x）]2+f（x2）的最大值为．【分析】根据f（x）的定义域为[1，9]先求出y＝[f（x）]2+f（x2）的定义域为[1，3]，然后利用二次函数的最值再求函数g（x）＝[f（x）]2+f（x2）＝（2+log3x）2+（2+log3x2）＝（log3x+3）2﹣3的最大值．【答案】解：由f（x）的定义域为[1，9]可得y＝[f（x）]2+f（x2）的定义域为[1，3]，又g（x）＝（2+log3x）2+（2+log3x2）＝（log3x+3）2﹣3，∵1≤x≤3，∴0≤log3x≤1．∴当x＝3时，g（x）有最大值13．故答案为：13【点睛】根据f（x）的定义域，先求出g（x）的定义域是正确解题的关键步骤，属于易错题．【考点9 与对数函数的单调性有关的问题】【例9】（2019春•吉林期末）已知函数f（x）＝log a（x+3）﹣log a（3﹣x），a＞0且a≠1．（1）求函数f（x）的定义域；（2）判断并证明函数f（x）的奇偶性；（3）若a＞1，指出函数的单调性，并求函数f（x）在区间[0，1]上的最大值．【分析】（1）由题意可得，从而求定义域；（2）可判断函数f（x）是奇函数，再证明如下；（3）当a＞1时，由复合函数的单调性及四则运算可得f（x）为增函数，从而求最值．【答案】解：（1）由题意知，；解得，﹣3＜x＜3；故函数f（x）的定义域为（﹣3，3）；（2）函数f（x）是奇函数，证明如下，函数f（x）的定义域（﹣3，3）关于原点对称；则f（﹣x）＝log a（﹣x+3）﹣log a（3+x）＝﹣f（x），故函数f（x）是奇函数．（3）当a＞1时，由复合函数的单调性及四则运算可得，f（x）＝log a（x+3）﹣log a（3﹣x）为增函数，则函数f（x）在区间[0，1]上单调递增，故f max（x）＝f（1）＝log a2．【点睛】本题考查了函数的定义域，奇偶性，单调性，最值的判断与应用，属于基础题．【变式9-1】（2018秋•南岗区校级期中）已知f（x）＝log a（a＞0，且a≠1，m≠﹣1）是定义在区间（﹣1，1）上的奇函数，（1）求f（0）的值和实数m的值；（2）判断函数f（x）在区间（﹣1，1）上的单调性，并说明理由；（3）若f（）＞0且f（b﹣2）+f（2b﹣2）＞0成立，求实数b的取值范围．【分析】（1）根据奇函数的特性，可得f（0）＝0，再由f（﹣x）＝﹣f（x），m≠﹣1，可得实数m的值；（2）结合对数函数的图象和性质，及复合函数同增异减的原则，可得函数f（x）在区间（﹣1，1）上的单调性；（3）由f（）＞0，可得函数f（x）在区间（﹣1，1）上的单调递增，结合函数的定义域和奇偶性，解不等式，可得实数b的取值范围．【答案】解：（1）∵f（x）＝log a（a＞0，且a≠1，m≠﹣1）是定义在区间（﹣1，1）上的奇函数，∴f（0）＝0，且f（﹣x）＝﹣f（x），即＝﹣，即+＝＝log a1＝0，故m2＝1，又∵m≠﹣1，故m＝1，（2）由（1）得f（x）＝＝，令t＝，则t在区间（﹣1，1）上单调递减，当0＜a＜1时，y＝log a t为减函数，此时函数f（x）在区间（﹣1，1）上的单调递增；当a＞1时，y＝log a t为增函数，此时函数f（x）在区间（﹣1，1）上的单调递减；（3）若f（）＝＞0，则0＜a＜1，由（1）得，函数f（x）在区间（﹣1，1）上的单调递增，若f（b﹣2）+f（2b﹣2）＞0，则f（b﹣2）＞﹣f（2b﹣2），则f（b﹣2）＞f（2﹣2b），则﹣1＜2﹣2b＜b﹣2＜1，解得：b∈（，）【点睛】本题考查的知识点是对数函数的图象与性质，难度不大，属于基础题．【变式9-2】（2019秋•番禺区校级期中）已知函数．（1）求函数的定义域．（2）讨论函数f（x）的奇偶性．（3）判断函数f（x）的单调性，并用定义证明．【分析】（1）解不等式得出x的范围，从而得出函数f（x）的定义域；（2）将﹣x代入函数f（x）的解析式，利用对数的运算性质得到f（﹣x）＝﹣f（x），从而得出答案；（3）在区间（1，+∞）上任取x1＞x2＞1，作差f（x1）﹣f（x2），通过对数的运算性质以及对数函数的单调性得出差值f（x1）﹣f（x2）的符号，从而得出函数f（x）在区间（1，+∞）上的单调性，再利用同样的方法可得出函数f（x）在区间（﹣∞，1）上的单调性．【答案】解：（1），零和负数无对数，，可得x＜﹣1或x＞1，则定义域为（﹣∞，﹣1）∪（1，+∞）；（2）函数f（x）的定义域为（﹣∞，﹣1）∪（1，+∞），关于原点对称，＝，因此，函数f（x）为奇函数；（3）函数f（x）在区间（﹣∞，﹣1）和（1，+∞）上都是减函数，下面利用定义来证明．先利用定义证明函数f（x）在区间（1，+∞）上的单调性．任取x1＞x2＞1，则＝＝，∵x1＞x2＞1，则x1x2+x2﹣x1﹣1＜x1x2+x1﹣x2﹣1，此时，g a1＝0，即f（x1）＜f（x2），所以，函数f（x）在区间（1，+∞）上单调递减，同理可证函数f（x）在区间（﹣∞，﹣1）上也为减函数．【点睛】本题考察函数的定义域的求解，考察对数型函数的奇偶性与单调性的定义，关键在于利用定义来判断函数的基本性质，以及熟悉定义法判断函数基本性质的基本步骤，属于中等题．【变式9-3】（2019秋•荔湾区校级期末）已知函数f（x）＝log3（1+x）﹣log3（1﹣x）．（1）求函数f（x）定义域，并判断f（x）的奇偶性．（2）判断函数f（x）在定义域内的单调性，并用单调性定义证明你的结论．（3）解关于x的不等式f（1﹣x）+f（1﹣x2）＞0．【分析】（1）根据对数函数的性质以及函数的定义域，根据函数的奇偶性的定义判断函数的奇偶性即可；（2）根据函数单调性的定义判断函数的单调性即可；（3）根据函数的单调性以及函数的奇偶性判断即可．【答案】解：（1）要使函数f（x）＝log3（1+x）﹣log3（1﹣x）有意义，必须满足，解得：﹣1＜x＜1，∴函数f（x）的定义域是（﹣1，1），综上所述，结论是：函数f（x）的定义域是（﹣1，1）．f（x）＝log3（1+x）﹣log3（1﹣x）＝log3（）．f（﹣x）＝log3＝﹣log3．∴f（x）为奇函数．（2）函数f（x）＝log3（），在区间（﹣1，1）上任取两个不同的自变量x1，x2，且设x1＜x2，则f（x1）﹣f（x2）＝log3，又（1+x1）（1﹣x2）﹣（1﹣x1）（1+x2）＝2（x1﹣x2）＜0，即（1+x1）（1﹣x2）＜（1﹣x1）（1+x2），∵﹣1＜x1＜x2＜1，∴1+x1＞0，1﹣x2＞0，∵（1+x1）（1﹣x2）＞0，∴＜1，∴log3＜0，即f（x1）＞f（x2），∴函数f（x）是定义域内的单调递增函数．（3）∵f（x）为奇函数，∴f（1﹣x）+f（1﹣x2）＞0∴f（1﹣x）＞f（x2﹣1），又∵f（x）在定义域上单调递增，∴1﹣x＞x2﹣1，x2+x﹣2＜0，即（x+2）（x﹣1）＜0，∴﹣2＜x＜1，而，解得：0＜x＜，综上：0＜x＜1．【点睛】本题考查了函数的单调性、奇偶性问题，考查导数的应用以及转化思想，是一道中档题．。

更上一层楼基础·巩固·达标1.已知函数f(x)=lgxx +-11若.f(a)=b,则f(-a)的值为（ ） A.b B.-b C.b 1 D.-b1 思路解析：∵f(x)=lg(xx +-11), ∴f(-x)=lg x x -+11=lg(x x +-11)-1=-lg x x +-11, ∴f(-a)=-f(a)=-b.答案：B2.若定义在区间（-1，0）内的函数f （x ）=log 2a （x+1）满足f （x ）>0，则a 的取值范围是（ ）A.（0，21）B.（0，1）C.（21，+∞） D.（0，+∞） 思路解析：∵-1<x<0，∴0<x+1<1.由f （x ）=log 2a （x+1）>0，可得0<2a<1，即0<a<21.也可采用定量分析与特殊值代入相结合的方法求解.∵2a ≠1，∴a ≠21，可排除答案B 、D 项.再从A 项或C 项中任选一特殊值，又可排除其中一个答案.答案：A3.若函数y=f （x ）的定义域为［21，2］，则函数y=f （log 2x ）的定义域为（ ） A.［-1，1］ B.［21，2］ C.［1，2］ D.［2，4］ 思路解析：由题意得21≤log 2x ≤2，即log 22≤log 2x ≤log 24，解得2≤x ≤4. 答案：D4.已知函数y=log a （2-ax ）在区间［0，1］上是x 的减函数，则a 的范围是（ ）A.（0，1）B.（1，2）C.（0，2）D.（2，+∞） 思路解析：令u=2-ax ，x ∈［0，1］，∵a>0且a ≠1，∴u 是x 的减函数.又∵y=log a （2-ax ）是减函数.∴y=log a u 是增函数.∴a>1.又∵2-ax>0，x ∈［0，1］，∴a<2.∴1<a<2.答案：B5.某种细菌在培养过程中，每20分钟分裂一次（一个分裂为两个），经__________小时后，这种细菌可由1个分裂成512个（ ）A.1B.2C.3D.4思路解析：设分裂n 次后可由1个分裂成512个.则2n =512，∴n=log 2512=log 229=9.∴时间t=60920⨯=3 h. 答案：C6.已知0＜x ＜y ＜a ＜1，则有（ ）A.log a （xy ）＜0B.0＜log a （xy ）＜1C.1＜log a （xy ）＜2D.log a （xy ）＞2思路解析：∵0＜x ＜a ＜1，∴log a x ＞log 记分=1.又0＜y ＜a ＜1，∴log a y ＞log 记分=1.∴log a x+log a y=log a （xy ）＞2.答案：D7.若函数f(x)=log a x （0<a<1）在区间[a,2a]上的最大值是最小值的3倍,则a 的值为（ ） A.42 B.22 C.41 D.21 思路解析：∵0<a<1,∴f(x)=log a x 是单调减函数．从而有：f(a)=3f(2a)即log 记分=3log a （2a ）,化简为（2a ）3=a>0,解得a=42. 答案：A综合·应用·创新 8.函数y=log 2xx --312的定义域为_____________________. 思路解析：由x x --312>0可得21＜x ＜3. 答案：（21，3） 9.若f （x ）=⎪⎩⎪⎨⎧+∞∈-∞∈],,1(,log ],1,(,)21(81x x x x 则满足f （x ）=41的x 的值为________________. 思路解析：当x ≤1时，f （x ）=(21)x ≥21，∴满足f （x ）=41的x ∈（1，+∞），即log 81x=41.∴x=481=3. 答案：310.三个数60.7，0.76，log 0.76的大小关系为____________________.思路解析：∵60.7>60=1，0.76<0.70=1，∴60.7>1，0<0.76<1.又∵log 0.76<0，∴log 0.76<0.76<60.7.答案：log 0.76<0.76<60.7.11.函数f(x)=log 2(1+x -1)(x>8)的值域是___________________.思路解析：∵x>8∴1+x -1>2由于对数函数的底数2大于1，说明函数为增函数．所以f(x)>log 22=1,故函数的值域为(1,+∞).答案：(1,+∞)12.已知函数f （x ）=11log --x mx a （a ＞0，且a ≠1）的图象关于原点对称.求m 的值.思路解析：根据已知条件，对于定义域内的一切x ，都有f （-x ）=-f （x ），即f （-x ）+f （x ）=0，∴log a 11--+x mx +log a 11--x mx =0. 整理得log a 11222--x x m =0，∴11222--x x m =1，即（m 2-1）x 2=0. ∴m 2-1=0.∴m=1或m=-1.若m=1，11--x mx =-1，f （x ）无意义， 则舍去m=1，∴m=-1.答案：m=-1。

高中数学学习材料马鸣风萧萧*整理制作2.2.2 对数函数及其性质 第1课时 对数函数的图象及性质基础达标1．函数f (x )＝11－x＋lg(1＋x )的定义域是 ( )．A ．(－∞，－1)B ．(1，＋∞)C ．(－1,1)∪(1，＋∞)D ．(－∞，＋∞)解析 要使函数有意义，须满足：⎩⎨⎧1－x ≠0，1＋x >0，解之得x >－1且x ≠1.故其定义域为(－1,1)∪(1，＋∞)． 答案 C2．已知a >0且a ≠1，函数y ＝a x 与y ＝log a (－x )的图象可能是下图中的( )．解析 y ＝log a (－x )的图象与y ＝log a x 的图象关于y 轴对称． 又y ＝a x 与y ＝log a x 的单调性相同应选B. 答案 B3．已知log a 13>log b 13>0，则下列关系正确的是( )．A ．0<b <a <1B ．0<a <b <1C ．1<b <aD ．1<a <b解析 由log a 13>0，log b 13>0，可知a ，b ∈(0,1)，又log a 13>log b 13作出图象如图所示，结合图象易知a >b ，∴0<b <a <1. 答案 A 4．函数f (x )＝lg (4－x )x －3的定义域为________． 解析 由⎩⎨⎧4－x >0，x －3≠0，解得x <4，且x ≠3，所以定义域为{x |x <4，且x ≠3}．答案 {x |x <4，且x ≠3}5．若函数f (x )＝a x (a >0且a ≠1)的反函数的图象过点(2，－1)，则a ＝________. 解析 f (x )＝a x 的反函数为g (x )＝log a x ，图象过点(2，－1)，∴－1＝log a 2，∴a ＝12. 答案 12 6．已知函数y ＝log a2x ＋1x －1的图象恒过点P ，则点P 坐标为________． 解析 当2x ＋1x －1＝1时，x ＝－2，所以恒过点(－2,0)． 答案 (－2,0) 7．已知f (x )＝log 3x .(1)作出这个函数的图象；(2)当0<a <2时， 利用图象判断是否有满足f (a )>f (2)的a 值． 解 (1)作出函数y ＝log 3x 的图象如图所示：(2)令f (x )＝f (2)，即log 3x ＝log 32，解得x ＝2.由如图所示的图象知：当0<a <2时， 恒有f (a )<f (2)．故当0<a <2时，不存在满足f (a )>f (2)的a 值．能力提升8．函数f (x )＝1＋log 2x 与g (x )＝21－x 在同一直角坐标系下的图象大致是( )．解析 由对数函数y ＝log 2x 过定点(1,0)可知， 函数f (x )＝1＋log 2x 的图象过定点(1,1)，且是单调递增的．同理，函数g (x )＝21－x 的图象过定点(1,1)，并且是单调递减的．观察函数图象可得选项C 满足条件． 答案 C9．若定义在区间(－1,0)内的函数f (x )＝log 2a (x ＋1)满足f (x )>0，则a 的取值范围是________．解析 当－1<x <0时，0<x ＋1<1， 又f (x )＝log 2a (x ＋1)>0， ∴0<2a <1，则0<a <12. 答案 ⎝ ⎛⎭⎪⎫0，1210．若函数f (x )为定义在R 上的奇函数，且x ∈(0，＋∞)时，f (x )＝lg(x ＋1)，求f (x )的表达式，并画出大致图象． 解 ∵f (x )为R 上的奇函数，∴f (0)＝0. 又当x ∈(－∞，0)时，－x ∈(0，＋∞)， ∴f (－x )＝lg(1－x )． 又f (－x )＝－f (x )， ∴f (x )＝－lg(1－x )， ∴f (x )的解析式为f (x )＝⎩⎨⎧lg (x ＋1)，x >0，0， x ＝0，－lg (1－x )，x <0，∴f (x )的大致图象如图所示：。

2.2.2 对数函数及其性质(二)一、基础过关1． 若函数y ＝f (x )的定义域是[2,4]，则y ＝f (log 12x )的定义域是 ( )A ．[12，1]B ．[4,16]C ．[116，14]D ．[2,4]2． 当a ＞1时，函数y ＝log a x 和y ＝(1－a )x 的图象只可能是 ()3． 设a ＝log 54，b ＝(log 53)2，c ＝log 45，则 ()A ．a ＜c ＜bB ．b ＜c ＜aC ．a ＜b ＜cD ．b ＜a ＜c4． 函数y ＝3x (－1≤x ＜0)的反函数是 ( )A ．y ＝log 13x (x ＞0) B ．y ＝log 3x (x ＞0)C ．y ＝log 3x (13≤x ＜1) D ．y ＝log 13x (13≤x ＜1) 5． 函数f (x )＝lg (2x －b )，若x ≥1时，f (x )≥0恒成立，则b 应满足的条件是________．6． 不等式log 12(4x ＋2x ＋1)＞0的解集为________． 7． 已知函数f (x )＝lg(x ＋1)．若0<f (1－2x )－f (x )<1，求x 的取值范围．8． 已知f (x )＝log a (3－ax )在x ∈[0,2]上单调递减，求a 的取值范围．二、能力提升9． 已知函数y ＝log 2(x 2－2kx ＋k )的值域为R ，则k 的取值范围是 ( )A ．0＜k ＜1B ．0≤k ＜1C ．k ≤0或k ≥1D ．k ＝0或k ≥110．函数f (x )＝a x＋log a (x ＋1)在[0,1]上的最大值与最小值之和为a ，则a 的值为( )A.14B.12C ．2D ．411．函数y ＝log a x 当x ＞2时恒有|y |＞1，则a 的取值范围是________．12．已知函数f (x )＝log 121－ax x －1的图象关于原点对称，其中a 为常数． (1)求a 的值；(2)若当x ∈(1，＋∞)时，f (x )＋log 12(x －1)<m 恒成立．求实数m 的取值范围． 三、探究与拓展13．已知f (x )＝2＋log 3x ，x ∈[1,9]，求y ＝[f (x )]2＋f (x 2)的最大值以及y 取最大值时x 的值．答案1．C 2．B 3．D 4．C 5．b ≤1 6．(－∞，log 2(2－1))7． 解 由⎩⎪⎨⎪⎧ 2－2x >0，x ＋1>0得－1<x <1. 由0<lg(2－2x )－lg(x ＋1)＝lg 2－2x x ＋1<1得1<2－2xx ＋1<10.因为x ＋1>0，所以x ＋1<2－2x <10x ＋10，解得－23<x <13.由⎩⎪⎨⎪⎧ －1<x <1，－23<x <13得－23<x <13.8． 解 由a >0可知u ＝3－ax 为减函数，依题意则有a >1.又u ＝3－ax 在[0,2]上应满足u >0，故3－2a >0，即a <32.综上可得，a 的取值范围是1<a <32.9．C 10．B 11．[12，1)∪(1,2]12．解 (1)∵函数f (x )的图象关于原点对称，∴函数f (x )为奇函数，∴f (－x )＝－f (x )，即log 121＋ax－x －1＝－log 121－axx －1＝log 12x －11－ax ，解得a ＝－1或a ＝1(舍)．(2)f (x )＋log 12(x －1)＝log 121＋x x －1＋log 12(x －1)＝log 12(1＋x )，当x >1时，log 12(1＋x )<－1，∵当x ∈(1，＋∞)时，f (x )＋log 12(x －1)<m 恒成立，∴m ≥－1.13．解 ∵f (x )＝2＋log 3x ，∴y ＝[f (x )]2＋f (x 2)＝(2＋log 3x )2＋2＋log 3x 2＝(2＋log 3x )2＋2＋2log 3x＝(log 3x )2＋6log 3x ＋6＝(log 3x ＋3)2－3.∵函数f (x )的定义域为[1,9]，∴要使函数y ＝[f (x )]2＋f (x 2)有意义，必须满足⎩⎪⎨⎪⎧ 1≤x 2≤9，1≤x ≤9，∴1≤x ≤3，∴0≤log 3x ≤1.∴6≤y ＝(log 3x ＋3)2－3≤13.当log 3x ＝1，即x ＝3时，y ＝13.∴当x ＝3时，函数y ＝[f (x )]2＋f (x 2)取得最大值13.。

2.2.2对数函数及其性质（第二课时）1、设a ＝log 54，b ＝(log 53)2，c ＝log 45，则( )A ．a ＜c ＜bB ．b ＜c ＜aC ．a ＜b ＜cD ．b ＜a ＜c1、解、选D.a ＝log 54＜1，l og 53＜log 54＜1，b ＝(log 53)2＜log 53，c ＝log 45＞1，故b ＜a ＜c .2、已知f (x )＝log a |x －1|在(0,1)上递减，那么f (x )在(1，＋∞)上( )A ．递增无最大值B ．递减无最小值C ．递增有最大值D ．递减有最小值2、解、选A.设y ＝log a u ，u ＝|x －1|.x ∈(0,1)时，u ＝|x －1|为减函数，∴a >1.∴x ∈(1，＋∞)时，u ＝x －1为增函数，无最大值．∴f (x )＝log a (x －1)为增函数，无最大值．3、已知函数f (x )＝a x ＋log a x (a ＞0且a ≠1)在[1,2]上的最大值与最小值之和为log a 2＋6，则a 的值为( ) A.12 B.14 C ．2 D ．4 3、解、选C.由题可知函数f (x )＝a x ＋log a x 在[1,2]上是单调函数，所以其最大值与最小值之和为f (1)＋f (2)＝a＋log a 1＋a 2＋lo g a 2＝log a 2＋6，整理可得a 2＋a －6＝0，解得a ＝2或a ＝－3(舍去)，故a ＝2.4、函数y ＝log 13(－x 2＋4x ＋12)的单调递减区间是________．4、解、y ＝log 13u ，u ＝－x 2＋4x ＋12.令u ＝－x 2＋4x ＋12>0，得－2<x <6.∴x ∈(－2,2]时，u ＝－x 2＋4x ＋12为增函数，∴y ＝log 13(－x 2＋4x ＋12)为减函数．答案：(－2,2]5、判断函数f （x ）=ln （21x +－x ）的奇偶性.5、解：∵12+x ＞x 恒成立，故（x ）的定义域为（－∞，+∞），又∵f （－x ）=ln （21x ++x ）=－ln x x ++211=－ln 2222)1(1x x x x -+-+=－ln （21x +－x ）=－f （x ），∴f （x ）为奇函数.在根据函数的单调性的定义判断函数单调性的时候，首先应该根据函数的解析式确定函数的定义域，当所给函数的定义域关于原点对称时，再判断f （x ）和f （－x ）之间的关系.f （x ）为奇函数⇔f （－x ）=－f （x ）⇔f （x ）+f （－x ）=0⇔)()(x f x f -=－1〔f （x ）≠0〕，f （x ）为偶函数⇔f （－x ）=f （x ）⇔ f （－x ）－f （x ）=0⇔)()(x f x f -=1〔f （x ）≠0〕. 在解决具体问题时，可以根据函数解析式的具体特点选择不同的方式来判断.6、（1）证明函数f （x ）=log 2（x 2+1）在（0，+∞）上是增函数；（2）问：函数f （x ）=log 2（x 2+1）在（－∞，0）上是减函数还是增函数？6、分析：此题目的在于让学生熟悉函数单调性证明通法，同时熟悉利用对数函数单调性比较同底数对数大小的方法.（1）证明：设x 1、x 2∈（0，+∞），且x 1＜x 2，则f （x 1）－f （x 2）=log 2（x 12+1）－log 2（x 22+1），∵0＜x 1＜x 2，∴x 12+1＜x 22+1.又∵y =log 2x 在（0，+∞）上是增函数，∴log 2（x 12+1）＜log 2（x 22+1），即f （x 1）＜f （x 2）.∴函数f （x ）=log 2（x 2+1）在（0，+∞）上是增函数.（2）解：是减函数，证明可以仿照上述证明过程.小结：利用定义证明函数的单调性是研究单调性问题的重要方法.7、 已知f （log a x ）=)1()1(22--a x x a ，其中a ＞0，且a ≠1.（1）求f （x ）；（2）求证：f （x ）是奇函数；（3）求证：f（x ）在R 上为增函数.7、分析：利用换元法，可令t =log a x ，求出f （x ），从而求出f （x ）.证明奇函数及增函数可运用定义.（1）解：设t =log a x ，则t ∈R ，∴x =a t （x ＞0）.则f （t ）=)1()1(22--a a a a t t =12-a a（a t －a －t ）. （2）证明：∵f （－x ）=12-a a（a －x －a x ）=－12-a a （a x －a －x）=－f （x ）， ∴f （x ）为奇函数. （3）证明：设x 1、x 2∈R ，且x 1＜x 2，则f （x 2）－f （x 1）=12-a a [ （a 2x －a－2x ）－（a 1x －a －1x ）］=12-a a [（a 2x －a 1x ）+a －1x a －2x （a 2x －a 1x ）］ =12-a a（a 2x －a 1x ）（1+a －1x a －2x ）.若0＜a ＜1，则a 2－1＜0，a 1x ＞a 2x ，∴f （x 2）＞f （x 1）.∴y =f （x ）在R 上为增函数；若a ＞1，则a 2－1＞0，a 1x ＜a 2x . ∴f （x 2）＞f （x 1）.∴y =f （x ）在R 上为增函数.综上，a ＞0，且a ≠1时，y =f （x ）是增函数.8、 比较下列各组数的大小：（1）log 0.7 1.3和log 0.71.8；（2）log 35和log 64.（3）(lg n )1.7和(lg n )2 (n ＞1)；8、解、（1）对数函数y = log 0.7x 在(0, +∞)内是减函数. 因为1.3＜1.8，所以log 0.71.3＞log 0.71.8.（2）log 35和log 64的底数和真数都不相同，需找出中间量“搭桥”，再利用对数函数的单调性即可求解.因为log 35＞log 33 = 1 = log 66＞log 64，所以log 35＞log 64.（3）把lg n 看作指数函数的底，本题归为比较两个指数函数的函数值的大小，故需对底数lg n 讨论.若1＞ln n ＞0，即1＜n ＜10时，y = (lg n )x 在R 上是减函数，所以(lg n )1.7＞(lg n )2；若lg n ＞1，即n ＞10时，y = (lg n )2在R 上是增函数，所以(lg n )1.7＜(lg n )2.若ln n = 1，即n = 10时，(ln n )1.7 = (ln n )2.【小结】两个值比较大小，如果是同一函数的函数值，则可以利用函数的单调性来比较. 在比较时，一定要注意底数所在范围对单调性的影响，即a ＞1时是增函数，0＜a ＜1时是减函数，如果不是同一个函数的函数值，就可以对所涉及的值进行变换，尽量化为可比较的形式，必要时还可以“搭桥”——找一个与二者有关联的第三量，以二者与第三量（一般是–1、0、1）的关系，来判断二者的关系，另外，还可利用函数图象直观判断，比较大小方法灵活多样，是对数学能力的极好训练.9、求证：函数f (x ) =xx -1log 2在(0, 1)上是增函数.9、【分析】根据函数单调性定义来证明. 解、设0＜x 1＜x 2＜1，则f (x 2) – f (x 1) = 212221log log 11x x x x --- 21221(1)log (1)x x x x -=- =.11log 21122x x x x --⋅ ∵0＜x 1＜x 2＜1， ∴12x x ＞1，2111x x --＞1. 则2112211log x x x x --⋅＞0， ∴f (x 2)＞f (x 1). 故函数f (x )在(0, 1)上是增函数.。

第二课时1．函数f(x)＝log 4x 与f(x)＝4x的图象…( )A ．关于x 轴对称B ．关于y 轴对称C ．关于原点对称D ．关于直线y ＝x 对称 2．若定义在区间(－1,0)内的函数f(x)＝log 2a (x ＋1)满足f(x)＞0，则a 的取值范围为( )A ．(0，12) B ．(0,1)C ．(12，＋∞) D ．(0，＋∞)3．已知函数t ＝－144lg(1－N100)的图象可表示打字任务的“学习曲线”，其中N 表示每分钟打出的字数，t 表示达到打字水平N(字/分)所需的学习时间(分)，则按此曲线要达到90字/分的水平，所需要的学习时间为( )A ．72B ．100C ．144D ．2884．(2008上海高考，文4)函数f(x)的反函数为f －1(x)＝log 2x ，则f(x)＝__________.课堂巩固1．若f(x)＝log a x(a>0且a ≠1)，且反函数值f －1(2)<1，则f(x)的图象是( )2．设P ＝log 23，Q ＝log 32，R ＝log 2(log 32)，则( ) A ．R<Q<P B ．P<R<Q C ．Q<R<P D ．R<P<Q 3．(2009百校联考仿真卷三，1)已知集合M ＝{y|y ＝ln(x 2＋1)，x ∈R }，N ＝{x|2x <2，x ∈R }，则M ∩N 等于( )A ．[0，＋∞)B ．[0,1)C ．(1，＋∞)D ．(0,1]4．函数y ＝lg(21＋x－1)的图象关于( )A ．x 轴对称B ．y 轴对称C ．原点对称D ．直线y ＝x 对称5．函数f(x)＝a x ＋log a (x ＋1)在[0,1]上的最大值与最小值之和为a ，则a 的值为( ) A.14 B.12C ．2D ．4 6．若A ＝{x ∈Z |2≤22－x <8}，B ＝{x ∈R ||log 2x|>1}，则A ∩(∁R B)的元素个数是( ) A ．0 B ．1 C ．2 D ．37．函数y ＝log 2(1－x 2)的值域是__________． 8．解下列方程： (1)log 7(log 3x)＝－1； (2)2log x 25－3log 25x ＝1.9．分贝是计量声音强度相对大小的单位．物理学家引入了声压级(spl)来描述声音的大小：把一很小的声压p 0＝2×10－5帕作为参考声压，把所要测量的声压p 与参考声压p 0的比值取常用对数后乘以20得到的数值称为声压级．声压级是听力学中最重要的参数之一，单位是分贝(dB)．分贝值在60以下为无害区，60～110为过渡区，110以上为有害区．(1)根据上述材料，列出分贝y 与声压p 的函数关系式；(2)某地声压p ＝0.002帕，试问该地的声音分贝值在以上所说的什么区？声音环境是否为无害区？1．设a ＞1，且m ＝log a (a 2＋1)，n ＝log a (a －1)，p ＝log a (2a)，则m ，n ，p 的大小关系为…( ) A ．n ＞m ＞p B ．m ＞p ＞n C ．m ＞n ＞p D ．p ＞m ＞n2．函数f(x)＝1＋log 2x 与g(x)＝2－x ＋1在同一直角坐标系下的图象大致是( )3.已知函数f(x)＝log 2(x 2－ax ＋3a)在[2，＋∞)上是增函数，则实数a 的取值范围是( ) A ．(－∞，4) B ．(－4,4]C ．(－∞，－4)∪[2，＋∞)D ．[－4,4)4．(2008陕西高考，理7)已知函数f(x)＝2x ＋3，f －1(x)是f(x)的反函数，若mn ＝16，m ，n ∈(0，＋∞)，则f －1(m)＋f －1(n)的值为( )A ．－2B ．1C ．4D ．105．(2008山东高考，文12)已知函数f(x)＝log a (2x＋b －1)(a>0，a ≠1)的图象如图所示，则a ，b 满足的关系是…( )A ．0<a －1<b<1B ．0<b<a －1<1C ．0<b －1<a<1D ．0<a －1<b －1<16．已知f(x)是定义在R 上的奇函数，f(x)在(0，＋∞)上是增函数，且f(13)＝0，则不等式f(log 18x)<0的解集为( )A ．(0，12)B ．(12，＋∞)C ．(12，1)∪(2，＋∞)D ．(0，12)∪(2，＋∞)7．若规定⎪⎪⎪⎪⎪⎪a b c d ＝|ad －bc|，则不等式log 2⎪⎪⎪⎪⎪⎪1 11 x <0的解集是__________．8．设函数f(x)＝⎩⎪⎨⎪⎧2x －4，x ≤4，－log 2(x ＋1)，x>4，若f(a)＝18，则f(a ＋6)＝__________.9．抽气机每次抽出容器内空气的60%，要使容器内的空气少于原来的0.1 %，则至少要抽几次？(lg2≈0.301 0)10．已知集合A ＝{x|(12)x 2－x －6<1}，B ＝{x|log 4(x ＋a)<1}，若A ∩B ＝∅，求实数a 的取值范围．11．设函数f(x)＝x 2－x ＋b ，且f(log 2a)＝b ，log 2[f(a)]＝2(a ≠1)，求f(log 2x)的最小值及对应的x 的值．答案与解析第二课时 课前预习1．D 互为反函数的函数图象关于直线y ＝x 对称． 2．A 因为x ∈(－1,0)，所以x ＋1∈(0,1)． 此时f(x)＞0，根据图象得0＜2a ＜1，解得0＜a ＜12.3．C 将N ＝90代入，得t ＝－144lg(1－90100)＝144.4．2x课堂巩固1．B 因为f －1(x)＝a x ，f －1(2)<1，可知0<a<1.2．A 由对数函数的单调性知，0<log 32<1，即0<Q<1，又y ＝log 2x 是增函数， 所以R ＝log 2(log 32)<0.又log 23>log 22＝1，所以R<Q<P.3．B M ＝{y|y ≥0}，N ＝{x|x<1}，M ∩N ＝[0，＋∞)∩(－∞，1)＝[0,1)． 4．C f(x)＝lg(21＋x －1)＝lg 1－x1＋x，易知它是奇函数，图象关于原点对称．5．B 该函数在给定的区间上是单调函数，最值在区间的两个端点处取得，故a 0＋log a (0＋1)＋a ＋log a (1＋1)＝a ，解得a ＝12.6．C A ＝{0,1}，B ＝{x|x>2，或0<x<12}，∴A ∩(∁R B)＝{0,1}，其中的元素个数为2. 7．(－∞，0] 令u ＝1－x 2，则y ＝log 2u ，因为0<u ≤1，且由对数函数的单调性知y ＝log 2u 是增函数，所以y ≤0，即该函数的值域为(－∞，0]．8．解：(1)由题意，得log 3x ＝17，x ＝317.(2)设log 25x ＝t ，则log x 25＝1t.于是，原方程可化为2t －3t ＝1，化简，得3t 2＋t －2＝0.解得t ＝－1或t ＝23.当t ＝－1时，由log 25x ＝－1，得x ＝125；当t ＝23时，由log 25x ＝23，得x ＝543.综上可知，该方程的解是125或543.9．解：(1)由已知，得y ＝(lg p p 0)×20＝20lg pp 0(其中p 0＝2×10－5)．(2)将p ＝0.002代入函数关系y ＝20lg pp 0，则y ＝20lg 0.0022×10－5＝20lg102＝40(分贝)． 因为40分贝小于60分贝，所以该地在噪音无害区，环境优良．课后检测1．B ∵a ＞1，∴a 2＋1>2a,2a>a －1，且函数f(x)＝log a x 是增函数． ∴m ＞p ＞n.2．C 函数g(x)＝2－(x －1)的图象是由y ＝2－x 的图象向右平移1个单位而得到的；而f(x)＝1＋log 2x 的图象是由y ＝log 2x 的图象向上平移1个单位而得到的．3．B 令u(x)＝x 2－ax ＋3a ，其对称轴为x ＝a2.由题意有⎩⎪⎨⎪⎧u(2)＝4－2a ＋3a>0，a 2≤2.解得－4<a ≤4.4．A f(x)＝2x ＋3，得f －1(x)＝log 2x －3，于是f －1(m)＋f －1(n)＝log 2m －3＋log 2n －3＝log 2mn －6＝log 216－6＝4－6＝－2.5．A 由图易得a>1，∴0<a －1<1. 取特殊点x ＝0，得－1<log a b<0，即log a 1a<log a b<log a 1，∴0<a －1<b<1.6．C ∵f(x)在(0，＋∞)上是增函数，且f(13)＝0，在(0，＋∞)上f(log 18x)<0⇒f(log 18x)<f(13)⇒0<log 18x<13⇒log 181<log 18x<log 18(18)13⇒12<x<1；同理可求f(x)在(－∞，0)上是增函数，且f(－13)＝0，得x>2.综上所述，x ∈(12，1)∪(2，＋∞)．7．(0,1)∪(1,2) ⎪⎪⎪⎪⎪⎪1 11 x ＝|x －1|， 由log2|x －1|<0，得0<|x －1|<1，即0<x<2，且x ≠1.8．－3 (1)当a ≤4时，2a －4＝18，解得a ＝1，此时f(a ＋6)＝f(7)＝－3；(2)当a>4时，－log 2(a ＋1)＝18，无解．9．解：设至少抽n 次才符合条件，则a·(1－60%)n <0.1%·a(设原来容器中的空气体积为a)． 即0.4n <0.001，两边取常用对数，得n·lg0.4<lg0.001，所以n>lg0.001lg0.4(因为lg0.4<0)．所以n>－32lg2－1≈7.5.故至少需要抽8次，才能使容器内的空气少于原来的0.1%.10．解：由(12)x 2－x －6<1，得x 2－x －6>0，解得x<－2，或x>3，即A ＝{x|x<－2，或x>3}． 由log 4(x ＋a)<1，得0<x ＋a<4， 解得－a<x<4－a ，即B ＝{x|－a<x<4－a}．∵A ∩B ＝∅，∴⎩⎪⎨⎪⎧－a ≥－2，4－a ≤3，解得1≤a ≤2，即实数a 的取值范围是[1,2]．点评：比较同底数的指数或对数不等式的大小关系时，一要明确底数的范围，因为它决定函数的单调性；二要确定相应的指数或真数的大小关系．它们一起确定函数值的大小关系．特别地，对于对数式还可考虑到真数大于零这一限制条件．11.解：由已知，得⎩⎪⎨⎪⎧log 22a －log 2a ＋b ＝b ，log 2(a 2－a ＋b)＝2，即⎩⎪⎨⎪⎧ log 2a(log 2a －1)＝0，a 2－a ＋b ＝4.①②由①，得log 2a ＝1(a ≠1)， ∴a ＝2.代入②，得b ＝2. ∴f(x)＝x 2－x ＋2.∴f(log 2x)＝log 22x －log 2x ＋2＝(log 2x －12)2＋74. ∴当log 2x ＝12时，f(log 2x)取得最小值74，此时x ＝ 2.。