聚焦新中考大一轮复习讲义数学答案

中考数学一轮复习第1讲：实数概念与运算一、夯实基础1、绝对值是6的数是________2、|21|-的倒数是________________。

3、2的平方根是_________.4、下列四个实数中，比－1小的数是（ ）A ．－2 B.0 C ．1 D ．25、在下列实数中,无理数是( )二、能力提升 6、小明家冰箱冷冻室的温度为－5℃，调高4℃后的温度为（ ） A ．4℃ B ．9℃ C ．－1℃ D ．－9℃ 7、定义一种运算☆，其规则为a ☆b =＋，根据这个规则、计算2☆3的值是（ ） A ．65 B ．C ．5D ．68、下列计算不正确的是（ ）（A ） （B ） （C ） （D 三、课外拓展9、实数a 、b 在数轴上位置如图所示，则|a|、|b|的大小关系是________。

四、中考链接10、数轴上的点A 到原点的距离是6，则点A 表示的数为（ ）131a 1b 1531222-+=-21139⎛⎫-= ⎪⎝⎭33-==A. 6或6- B. 6 C. 6- D. 3或3-11、如果a与1互为相反数，则a等于（）．A．2 B．2- C．1 D．1-12、下列哪一选项的值介于0.2与0.3之间？（）A、 4.84B、0.484C、0.0484D、0.0048413、― 2×63＝14、在﹣2，2，2这三个实数中，最小的是15、写出一个大于3且小于4的无理数。

参考答案一、夯实基础1、6和-62、23、4、A5、C二、能力提升6、C7、A8、A三、课外拓展>9、a b四、中考链接10、A11、C12、C13、-214、﹣215、解：∵π≈3.14…，∴3＜π＜4，故答案为：π（答案不唯一）．第2讲：整式与因式分解一、夯实基础1．计算（直接写出结果）①a ·a 3=③(b 3)4=④(2ab )3=⑤3x 2y ·)223y x -（=2．计算：2332)()(a a -+-＝ ．3．计算：)(3)2(43222y x y x xy -⋅⋅-＝ ．4．1821684=⋅⋅n n n ，求n ＝ ．5．若._____34,992213=-=⋅⋅++-m m y x y x y x n n m m 则二、能力提升6．若)5)((-+x k x 的积中不含有x 的一次项，则k 的值是（）A ．0B ．5C ．－5D ．－5或57．若))(3(152n x x mx x ++=-+，则m 的值为（）A ．－5B ．5C ．－2D ．28．若142-=y x ，1327+=x y ，则y x -等于（）A ．－5B ．－3C ．－1D ．19．如果552=a ，443=b ，334=c ，那么（）A ．a ＞b ＞cB ．b ＞c ＞aC ．c ＞a ＞bD ．c ＞b ＞a三、课外拓展10．①已知,2,21==mn a 求n m a a )(2⋅的值.②若的求n n n x x x 22232)(4)3(,2---=值11．若0352=-+y x ，求y x 324⋅的值．四、中考链接12．（龙口）先化简，再求值：（每小题5分，共10分）（1）x （x -1）+2x （x +1）－（3x -1）（2x -5），其中x =2．（2）342)()(m m m -⋅-⋅-，其中m =2-13、（延庆）已知，求下列各式的值：（1）； （2）．14、（鞍山）已知：，.求：（1）；（2）.15、计算：；参考答案一、夯实基础1．a 4，b 4，8a 3b 3，-6x 5y 3；2．0；3．-12x 7y 9；4．2；5．4二、能力提升6．B ；7．C ；8．B ；9．B ；三、课外拓展10．①161；②56； 11．8；四、中考链接12．(1)-3x 2+18x-5，19；(2)m 9，-512；13.（1）45；（2）5714.（1）9；（2）115.第3讲：分式检测一、夯实基础1．下列式子是分式的是( )A ．x 2B ．x x ＋1C ．x 2＋yD ．x 32．如果把分式2xy x ＋y 中的x 和y 都扩大3倍，那么分式的值( ) A ．扩大3倍 B ．缩小3倍C ．扩大9倍D ．不变3．当分式x －1x ＋2的值为0时，x 的值是( ) A ．0 B ．1 C ．－1 D ．－24．化简：(1)x 2－9x －3＝__________. (2)aa －1＋11－a＝__________. 二、能力提升5．若分式2a ＋1有意义，则a 的取值范围是( ) A ．a ＝0 B ．a ＝1 C ．a ≠－1 D ．a ≠06．化简2x 2－1÷1x －1的结果是( ) A ．.2x －1 B ．2x 3－1 C ．2x ＋1D ．2(x ＋1) 7．化简m 2－163m －12得__________；当m ＝－1时，原式的值为__________． 三、课外拓展8．化简⎝ ⎛⎭⎪⎫m 2m －2＋42－m ÷(m ＋2)的结果是( ) A ．0 B ．1 C ．－1 D ．(m ＋2)29．下列等式中，不成立的是( )A ．x 2－y 2x －y ＝x －y B ．x 2－2xy ＋y 2x －y ＝x －yC ．xy x 2－xy ＝y x －yD ．y x －x y ＝y 2－x 2xy10．已知1a －1b ＝12，则aba －b 的值是( )A ．12B ．－12C ．2D ．－211．当x ＝__________时，分式x －2x ＋2的值为零．12．计算（—）·的结果是（ ） A ． 4 B ． －4 C ．2a D ．－2a13．分式方程的解是（ ）A ．x=－2B ．x=2C ． x=±2 D．无解14．把分式中的,都扩大3倍，那么分式的值（）A ．扩大为原来的3倍B ．缩小为原来的C ．扩大为原来的9倍D ．不变四、中考链接15．(临沂)先化简，再求值：(1)⎝ ⎛⎭⎪⎫1－1a －1÷a 2－4a ＋4a 2－a ，其中a ＝－1.(2)3－x 2x －4÷⎝ ⎛⎭⎪⎫5x －2－x －2，其中x ＝3－3. 2-a a2+a aa a 24-2114339x x x +=-+-(0)xyx y x y +≠+x y 13参考答案一、夯实基础1．B B 项分母中含有字母．2．A 因为x 和y 都扩大3倍，则2xy 扩大9倍，x ＋y 扩大3倍，所以2xy x ＋y 扩大3倍．3．B 由题意得x －1＝0且x ＋2≠0，解得x ＝1.4．(1)x ＋3 (2)1 (1)原式＝(x ＋3)(x －3)x －3＝x ＋3；(2)原式＝a a －1－1a －1＝a －1a －1＝1.二、能力提升5．C 因为分式有意义，则a ＋1≠0，所以a ≠－1.6．C 原式＝2(x ＋1)(x －1)·(x －1)＝2x ＋1. 7．m ＋43 1 原式＝(m ＋4)(m －4)3(m －4)＝m ＋43.当m ＝－1时，原式＝－1＋43＝1. 三、课外拓展8．B 原式＝m 2－4m －2·1m ＋2＝(m ＋2)(m －2)m －2·1m ＋2＝1. 9．A x 2－y 2x －y ＝(x ＋y )(x －y )x －y＝x ＋y . 10．D 因为1a －1b ＝12，所以b －a ab ＝12，所以ab ＝－2(a －b )，所以ab a －b ＝－2(a －b )a －b＝－2.11．2 由题意得x －2＝0且x ＋2≠0，解得x ＝2.12. B13. B14. A四、中考链接15．解：(1)⎝⎛⎭⎪⎫1－1a －1÷a 2－4a ＋4a 2－a ＝a －2a －1·a (a －1)(a －2)2＝a a －2.当a ＝－1时，原式＝a a －2＝－1－1－2＝13.(2)3－x2x－4÷⎝⎛⎭⎪⎫5x－2－x－2＝3－x2(x－2)÷⎝⎛⎭⎪⎫5x－2－x2－4x－2＝3－x2(x－2)÷9－x2x－2＝3－x2(x－2)·x－2(3－x)(3＋x)＝12x＋6.∵x＝3－3，∴原式＝12x＋6＝36.第4讲：二次根式一、夯实基础1．使3x －1有意义的x 的取值范围是( )A ．x ＞13B ．x ＞－13C ．x ≥13D ．x ≥－132．已知y ＝2x －5＋5－2x －3，则2xy 的值为( ) A ．－15 B ．15 C ．－152 D ．1523．下列二次根式中，与3是同类二次根式的是( ) A ．18 B ．27 C ．23 D ．324．下列运算正确的是( )A ．25＝±5B ．43－27＝1C ．18÷2＝9D ．24·32＝6 5．估计11的值( )A ．在2到3之间B ．在3到4之间C ．在4到5之间D ．在5到6之间 二、能力提升6．若x ，y 为实数，且满足|x －3|＋y ＋3＝0，则⎝ ⎛⎭⎪⎫x y 2 012的值是__________．7．有下列计算：①(m 2)3＝m 6，②4a 2－4a ＋1＝2a －1，③m 6÷m 2＝m 3，④27×50÷6＝15，⑤212－23＋348＝143，其中正确的运算有__________．(填序号)三、课外拓展8．若x ＋1＋(y －2 012)2＝0，则x y ＝__________.9．当－1＜x＜3时，化简：x－2＋x2＋2x＋1＝__________.10．如果代数式4x－3有意义，则x的取值范围是________．11、比较大小：⑴3 5 2 6 ⑵11 －10 －1312、若最简根式m2－3 与5m+3 是同类二次根式，则m= .13、若 5 的整数部分是a，小数部分是b，则a－1b= 。

A、B、C、D、E、F六人赛棋，采用单循环制。

现在知道：A、B、C、D、E五人已经分别赛过5.4、3、2、l盘。

问：这时F已赛过盘。

2 (三帆中学考题)甲、乙、丙三人比赛象棋，每两人赛一盘.胜一盘得2分.平一盘得1分，输一盘得0分.比赛的全部三盘下完后，只出现一盘平局.并且甲得3分，乙得2分，丙得1分.那么，甲乙，甲丙，乙丙(填胜、平、负)。

3(西城实验考题)A、B、C、D、E、F六个选手进行乒乓球单打的单循环比赛(每人都与其它选手赛一场)，每天同时在三张球台各进行一场比赛，已知第一天B对D，第二天C对E，第三天D对F，第四天B对C，问：第五天A与谁对阵?另外两张球台上是谁与谁对阵?4 (人大附中考题)一个岛上有两种人：一种人总说真话的骑士，另一种是总是说假话的骗子。

一天，岛上的2003个人举行一次集会，并随机地坐成一圈，他们每人都声明：“我左右的两个邻居是骗子。

”第二天，会议继续进行，但是一名居民因病未到会，参加会议的2002个人再次随机地坐成一圈，每人都声明：“我左右的两个邻居都是与我不同类的人。

”问有病的居民是_________(骑士还是骗子)。

5 (西城实验考题)某班一次考试有52人参加，共考5个题，每道题做错的人数如下：题号 1 2 3 4 5人数 4 6 10 20 39又知道每人至少做对一道题，做对一道题的有7人，5道题全做对的有6人，做对2道题的人数和3道题的人数一样多，那么做对4道题的有多少人?预测1学校新来了一位老师，五个学生分别听到如下的情况：(1)是一位姓王的中年女老师，教语文课;(2)是一位姓丁的中年男老师，教数学课;(3)是一位姓刘的青年男老师，教外语课;(4)是一位姓李的青年男老师，教数学课;(5)是一位姓王的老年男老师，教外语课。

他们听到的情况各有一项正确，请问：真实情况如何?预测2某次考试，A，B，C，D，E五人的得分是互不相同的整数。

A说：“我得了94分。

”B说：“我在五人中得分最高。

2020年中考数学第一轮复习教案第三章图形的认识与三角形第十七讲三角形与全等三角形【中考真题考点例析】考点一：三角形三边关系例1 （温州）下列各组数可能是一个三角形的边长的是（）A．1，2，4 B．4，5，9 C．4，6，8 D．5，5，11对应练习1－1（长沙）如果一个三角形的两边长分别为2和4，则第三边长可能是（）A．2 B．4 C．6 D．8考点二：三角形内角、外角的应用例2 （2019青岛中考）如图，BD 是△ABC 的角平分线，AE⊥ BD ，垂足为F ．若∠ABC＝35°，∠ C＝50°，则∠CDE 的度数为（）A. 35°B. 40°C. 45°D. 50°对应练习2－1（2019年威海）把一块含有45°角的直角三角板与两条长边平行的直尺如图放置（直角顶点在直尺的一条长边上），若∠1＝23°，则∠2＝°对应练习2－2（2019年枣庄）将一副直角三角板按如图所示的位置放置，使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上，则∠α的度数是（）.A.45°B. 60°C. 75°D. 85°考点三：三角形全等的判定和性质例3 （2019年山东滨州）如图，在△OAB和△OCD中，OA=OB，OC=OD，OA>OC ，∠AOB=∠COD=40°，连接AC，BD交于点M，连接OM，下列结论：①AC=BD；②∠AMB=40°；③OM平分∠BOC；④MO平分∠BMC．其中正确的个数为（）A．4 B．3 C．2 D．1对应练习3－1 （天门）如图，已知△ABC ≌△ADE ，AB 与ED 交于点M ，BC 与ED ，AD 分别交于点F ，N ．请写出图中两对全等三角形（△ABC ≌△ADE 除外），并选择其中的一对加以证明．对应练习3－2 （宜宾）如图：已知D 、E 分别在AB 、AC 上，AB=AC ，∠B=∠C ，求证：BE=CD ． 考点四：全等三角形开放性问题例4 （云南）如图，点B 在AE 上，点D 在AC 上，AB=AD ．请你添加一个适当的条件，使△ABC ≌△ADE （只能添加一个）．（1）你添加的条件是 ．（2）添加条件后，请说明△ABC ≌△ADE 的理由．对应练习4－1 （昭通）如图，AF=DC ，BC ∥EF ，只需补充一个条件 ，就得△ABC ≌△DEF ．第十七讲 三角形与全等三角形 参考答案【中考真题考点例析】考点一：三角形三边关系例1答案：C 对应练习1－1答案：B 考点二：三角形内角、外角的应用例2答案：C 对应练习2－1答案：68 对应练习2－2 答案：C 考点三：三角形全等的判定和性质MOCD B例3 答案：B 对应练习3－1 答案：△AEM ≌△ACN ，△BMF ≌△DNF ，△ABN ≌△ADM ．选择△AEM ≌△ACN ，证明：∵△ADE ≌△ABC ，∴AE=AC ，∠E=∠C ，∠EAD=∠CAB ，∴∠EAM=∠CAN ，∵在△AEM 和△ACN 中，∠E ＝∠CAE ＝AC∠EAM ＝∠CAN∴△AEM ≌△ACN （ASA ）．对应练习3－2 答案：证明：在△ABE 和△ACD 中，⎪⎩⎪⎨⎧)公共角A(＝∠A ∠)已知AC(＝ AB )已知C(＝∠B ∠ ∴△ABE ≌△ACD （ASA ），∴BE=CD （全等三角形的对应边相等）．考点四：全等三角形开放性问题例4 答案：解：（1）∵AB=AD ，∠A=∠A ，∴若利用“AAS ”，可以添加∠C=∠E ，若利用“ASA ”，可以添加∠ABC=∠ADE ，或∠EBC=∠CDE ，若利用“SAS ”，可以添加AC=AE ，或BE=DC ，综上所述，可以添加的条件为∠C=∠E （或∠ABC=∠ADE 或∠EBC=∠CDE 或AC=AE 或BE=DC ）；故答案为：∠C=∠E ；（2）选∠C=∠E 为条件．理由如下：∵在△ABC 和△ADE 中，⎪⎩⎪⎨⎧AD ＝AB E＝∠C ∠A ＝∠A ∠ ∴△ABC ≌△ADE （AAS ）．对应练习4－1 答案：BC=EF ，解析：∵AF=DC ，∴AF+FC=CD+FC ，即AC=DF ，∵BC ∥EF ，∴∠EFC=∠BCF ，∵在△ABC 和△DEF 中，⎪⎩⎪⎨⎧DF ＝AC BCF＝∠EFC ∠BC ＝EF ∴△ABC ≌△DEF （SAS ）．故答案为：BC=EF ．【聚焦中考真题】 一、选择题 1.（湘西州）如图，一副分别含有30°和45°角的两个直角三角板，拼成如下图形，其中∠C=90°，∠B=45°，∠E=30°，则∠BFD 的度数是（ ）A ．15°B ．25°C ．30°D ．10°2．（鄂州）一副三角板有两个直角三角形，如图叠放在一起，则∠α的度数是（ ）A ．165°B ．120°C ．150°D ．135°3．（泉州）在△ABC 中，∠A=20°，∠B=60°，则△ABC 的形状是（ ）A ．等边三角形B ．锐角三角形C ．直角三角形D ．钝角三角形4．（宜昌）下列每组数分别表示三根木棒的长度，将它们首尾连接后，能摆成三角形的一组是（ ）A ．1，2，6B ．2，2，4C ．1，2，3D ．2，3，45．（衡阳）如图，∠1=100°，∠C=70°，则∠A 的大小是（ ）A ．10°B ．20°C ．30°D ．80°6．（河北）如图1，M 是铁丝AD 的中点，将该铁丝首尾相接折成△ABC ，且∠B=30°，∠C=100°，如图2．则下列说法正确的是（ ）A ．点M 在AB 上B ．点M 在BC 的中点处C ．点M 在BC 上，且距点B 较近，距点C 较远D ．点M 在BC 上，且距点C 较近，距点B 较远7．（铁岭）如图，在△ABC 和△DEC 中，已知AB=DE ，还需添加两个条件才能使△ABC ≌△DEC ，不能添加的一组条件是（ ）A．BC=EC，∠B=∠E B．BC=EC，AC=DCC．BC=DC，∠A=∠D D．∠B=∠E，∠A=∠D8．（台州）已知△A1B1C1△A2B2C2的周长相等，现有两个判断：①若A1B1=A2B2，A1C1=A2C2，则△A1B1C1≌△A2B2C2；②若∠A1=∠A2，∠B1=∠B2，则△A1B1C1≌△A2B2C2，对于上述的两个判断，下列说法正确的是（）A．①正确，②错误B．①错误，②正确C．①，②都错误D．①，②都正确9．（邵阳）如图所示，点E是矩形ABCD的边AD延长线上的一点，且AD=DE，连结BE交CD 于点O，连结AO，下列结论不正确的是（）A．△AOB≌△BOC B．△BOC≌△EOD C．△AOD≌△EOD D．△AOD≌△BOC10．（河北）一个正方形和两个等边三角形的位置如图所示，若∠3=50°，则∠1+∠2=（）A．90°B．100°C．130°D．180°11．（陕西）如图，在四边形ABCD中，AB=AD，CB=CD，若连接AC、BD相交于点O，则图中全等三角形共有（）A．1对B．2对C．3对D．4对二、填空题12.（威海）将一副直角三角板如图摆放，点C在EF上，AC经过点D．已知∠A=∠EDF=90°，AB=AC．∠E=30°，∠BCE=40°，则∠CDF= ．13．（黔东南州）在△ABC中，三个内角∠A、∠B、∠C满足∠B-∠A=∠C-∠B，则∠B= 度．14．（柳州）如图，△ABC≌△DEF，请根据图中提供的信息，写出x= ．15．（巴中）如图，已知点B、C、F、E在同一直线上，∠1=∠2，BC=EF，要使△ABC≌△DEF，还需添加一个条件，这个条件可以是．（只需写出一个）16．（郴州）如图，点D、E分别在线段AB，AC上，AE=AD，不添加新的线段和字母，要使△ABE≌△ACD，需添加的一个条件是（只写一个条件即可）．17.（达州）如图，在△ABC中，∠A=m°，∠ABC和∠ACD的平分线交于点A1，得∠A1；∠A1BC和∠A1CD的平分线交于点A2，得∠A2；…∠A2012BC和∠A2012CD的平分线交于点A2013，则∠A2013= 度．三、解答题18．（聊城）如图，四边形ABCD中，∠A=∠BCD=90°，BC=CD，CE⊥AD，垂足为E，求证：AE=CE．19．（菏泽）如图，在△ABC中，AB=CB，∠ABC=90°，D为AB延长线上一点，点E在BC边上，且BE=BD，连结AE、DE、DC．（1）求证：△ABE≌△CBD；（2）若∠CAE=30°，求∠BDC的度数．20．（临沂）如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．（1）求证：AF=DC；（2）若AB⊥AC，试判断四边形ADCF的形状，并证明你的结论．21．（东营）（1）如图（1），已知：在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．证明：DE=BD+CE．（2）如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．（3）拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA=∠AEC=∠BAC，试判断△DEF的形状．22．（烟台）已知，点P是直角三角形ABC斜边AB上一动点（不与A，B重合），分别过A，B向直线CP作垂线，垂足分别为E，F，Q为斜边AB的中点．（1）如图1，当点P与点Q重合时，AE与BF的位置关系是，QE与QF 的数量关系式；（2）如图2，当点P在线段AB上不与点Q重合时，试判断QE与QF的数量关系，并给予证明；（3）如图3，当点P在线段BA（或AB）的延长线上时，此时（2）中的结论是否成立？请画出图形并给予证明．23．（玉林）如图，AB=AE，∠1=∠2，∠C=∠D．求证：△ABC≌△AED．24．（湛江）如图，点B、F、C、E在一条直线上，FB=CE，AB∥ED，AC∥FD，求证：AC=DF．25.（荆州）如图，△ABC与△CDE均是等腰直角三角形，∠ACB=∠DCE=90°，D在AB上，连结BE．请找出一对全等三角形，并说明理由．26．（十堰）如图，点D，E在△ABC的边BC上，AB=AC，BD=CE．求证：AD=AE．27.（佛山）课本指出：公认的真命题称为公理，除了公理外，其他的真命题（如推论、定理等）的正确性都需要通过推理的方法证实．（1）叙述三角形全等的判定方法中的推论AAS；（2）证明推论AAS．要求：叙述推论用文字表达；用图形中的符号表达已知、求证，并证明，证明对各步骤要注明依据．28．（内江）已知，如图，△ABC和△ECD都是等腰直角三角形，∠ACD=∠DCE=90°，D为AB边上一点．求证：BD=AE．29．（舟山）如图，△ABC与△DCB中，AC与BD交于点E，且∠A=∠D，AB=DC．（1）求证：△ABE≌DCE；（2）当∠AEB=50°，求∠EBC的度数？30．（荆门）如图1，在△ABC中，AB=AC，点D是BC的中点，点E在AD上．（1）求证：BE=CE；（2）如图2，若BE的延长线交AC于点F，且BF⊥AC，垂足为F，∠BAC=45°，原题设其它条件不变．求证：△AEF≌△BCF．31．（随州）如图，点F 、B 、E 、C 在同一直线上，并且BF=CE ，∠ABC=∠DEF ．能否由上面的已知条件证明△ABC ≌△DEF ？如果能，请给出证明；如果不能，请从下列三个条件中选择一个合适的条件，添加到已知条件中，使△ABC ≌△DEF ，并给出证明．提供的三个条件是：①AB=DE ；②AC=DF ；③AC ∥DF ．第十七讲 三角形与全等三角形 参考答案【聚焦中考真题】一、选择题1-5 AADDC 6-10 CCDAB 11 C二、填空题12答案：25°13答案：6014答案：2015答案：CA=FD16答案：∠B=∠C17答案：20152m解：∵A1B 平分∠ABC ，A1C 平分∠ACD ，∴∠A1=21∠A ，∠A2=21∠A1=221∠A ，… ∴∠A2 015=201521∠A=20152m 。

中考数学一轮复习平行四边形(讲义及答案)含答案一、解答题1．如图1，ABC ∆是以ACB ∠为直角的直角三角形，分别以AB ，BC 为边向外作正方形ABFG ，BCED ，连结AD ，CF ，AD 与CF 交于点M ，AB 与CF 交于点N ．（1）求证：ABD FBC ∆≅∆；（2）如图2，在图1基础上连接AF 和FD ，若6AD =，求四边形ACDF 的面积．2．综合与实践．问题情境：如图①，在纸片ABCD □中，5AD =，15ABCD S =，过点A 作AE BC ⊥，垂足为点E ，沿AE 剪下ABE △，将它平移至DCE '的位置，拼成四边形AEE D '．独立思考：（1）试探究四边形AEE D '的形状．深入探究：（2）如图②，在（1）中的四边形纸片AEE D '中，在EE '．上取一点F ，使4EF =，剪下AEF ，将它平移至DE F ''的位置，拼成四边形AFF D '，试探究四边形AFF D '的形状；拓展延伸：（3）在（2）的条件下，求出四边形AFF D '的两条对角线长；（4）若四边形ABCD 为正方形，请仿照上述操作，进行一次平移，在图③中画出图形，标明字母，你能发现什么结论，直接写出你的结论．3．（1）如图①，在正方形ABCD 中，AEF ∆的顶点E ，F 分别在BC ，CD 边上，高AG 与正方形的边长相等，求EAF ∠的度数；（2）如图②，在Rt ABD ∆中，90,BAD AD AB ︒∠==，点M ，N 是BD 边上的任意两点，且45MAN ︒∠=，将ABM ∆绕点A 逆时针旋转90度至ADH ∆位置，连接NH ，试判断MN ，ND ，DH 之间的数量关系，并说明理由；（3）在图①中，连接BD 分别交AE ，AF 于点M ，N ，若正方形ABCD 的边长为12，GF=6，BM= 32EG ，MN 的长．4．如图，在边长为1的正方形ABCD 中，E 是边CD 的中点，点P 是边AD 上一点（与点A D 、不重合），射线PE 与BC 的延长线交于点Q ．（1）求证：PDE QCE ∆≅∆；（2）若PB PQ =，点F 是BP 的中点，连结EF AF 、，①求证：四边形AFEP 是平行四边形；②求PE 的长．5．如图，在矩形ABCD 中，∠BAD 的平分线交BC 于点E ，AE =AD ，作DF ⊥AE 于点F ． （1）求证：AB ＝AF ；（2）连BF 并延长交DE 于G ．①EG ＝DG ；②若EG ＝1，求矩形ABCD 的面积．6．猜想与证明：如图①摆放矩形纸片ABCD 与矩形纸片ECGF ，使B ，C ，G 三点在一条直线上，CE 在边CD 上．连结AF ，若M 为AF 的中点，连结DM ，ME ，试猜想DM 与ME 的数量关系，并证明你的结论．拓展与延伸：(1)若将“猜想与证明”中的纸片换成正方形纸片ABCD 与正方形纸片ECGF ，其他条件不变，则DM 和ME 的关系为__________________；(2)如图②摆放正方形纸片ABCD 与正方形纸片ECGF ，使点F 在边CD 上，点M 仍为AF 的中点，试证明(1)中的结论仍然成立．[提示：直角三角形斜边上的中线等于斜边的一半]①②7．已知：在矩形ABCD中，点F为AD中点,点E为AB边上一点，连接CE、EF、CF，EF平分∠AEC．(1)如图1，求证：CF⊥EF;(2)如图2，延长CE、DA交于点K, 过点F作FG∥AB交CE于点G若，点H为FG上一点，连接CH,若∠CHG=∠BCE, 求证：CH=FK;(3)如图3, 过点H作HN⊥CH交AB于点N,若EN=11,FH-GH=1,求GK长.8．定义：只有一组对角是直角的四边形叫做损矩形，连结它的两个非直角顶点的线段叫做这个损矩形的直径。

2020年中考数学第一轮复习第一章 数与式第四节 因式分解【基础知识回顾】一、因式分解的定义：1、把一个 式化为几个整式 的形式，叫做把一个多项式因式分解。

2、因式分解与整式乘法是运算，即：多项式 整式的积 【注意：判断一个运算是否是因式分解或判断因式分解是否正确，关键看等号右边是否为 的形式。

】二、因式分解常用方法：1、提公因式法：公因式：一个多项式各项都有的因式叫做这个多项式各项的公因式。

提公因式法分解因式可表示为：ma+mb+mc= 。

【注意：1、公因式的选择可以是单项式，也可以是 ，都遵循一个原则：取系数的 ，相同字母的 。

2、提公因式时，若有一项被全部提出，则括号内该项为 ，不能漏掉。

3、提公因式过程中仍然要注意符号问题，特别是一个多项式首项为负时，一般应先提取负号，注意括号内各项都要 。

】2、运用公式法：将乘法公式反过来对某些具有特殊形式的多项式进行因式分解，这种方法叫做公式法。

①平方差公式：a 2-b 2= ,②完全平方公式：a 2±2ab+b 2= 。

【注意：1、运用公式法进行因式分解要特别掌握两个公式的形式特点，找准里面的a 与b 。

如：x 2-x+14符合完全平方公式形式，而x 2- x+12就不符合该公式的形式。

】 三、因式分解的一般步骤1、 一提：如果多项式的各项有公因式，那么要先 。

2、 二用：如果各项没有公因式，那么可以尝试运用 法来分解。

3、 三查：分解因式必须进行到每一个因式都不能再分解为止。

【注意：分解因式不彻底是因式分解常见错误之一，中考中的因式分解题目一般为两步，做题时要特别注意，另外分解因式的结果是否正确可以用整式乘法来检验】【中考真题考点例析】考点一：因式分解的概念A ．a （x-y ）=ax-ayB ．x +2x+1=x （x+2）+1C ．（x+1）（x+3）=x 2+4x+3D ．x 3-x=x （x+1）（x-1）考点二：因式分解例2. （2019山东东营）因式分解：x(x-3)-x+3= ．对应练习2－1．（2019年济南）分解因式：244m m -+=_____．（ ） （ ）对应练习2－2．（2019年莱芜）分解因式：a 3﹣4ab 2= ．考点三：因式分解的应用例1. 答案：6，1对应练习1－1． 答案：D考点二：因式分解例2. 答案：B对应练习2－1． 答案：2(2)m -对应练习2－2． 答案：a （a+2b ）（a ﹣2b ）考点三：因式分解的应用例3. 答案：4对应练习3－1． 答案：18【聚焦中考真题】一、选择题：1．（2019年山东临沂）将a 3b －ab 进行因式分解，正确的是（ ）A ．a(a 2b －b)B ．ab(a －1)2C ．ab(a+1)(a －1)D ．ab(a 2－1)2．（2019潍坊）下列因式分解正确的是（ ）A ．3ax 2－6ax=3(ax 2－2ax)B ．x 2+y 2=(－x+y)(－x －y)C ．a 2+2ab －4b 2=(a+2b)2D ．－ax 2+2ax －a=－a(x －1)23.（南昌）下列因式分解正确的是（ ） A ．x 2-xy+x=x （x -y ） B ．a 3-2a 2b+ab 2=a （a -b ）2C ．x 2-2x+4=（x -1）2+3D ．ax 2-9=a （x+3）（x -3）4．（张家界）下列各式中能用完全平方公式进行因式分解的是（ ）A ．x 2+x+1B ．x 2+2x-1C ．x 2-1D ．x 2-6x+95．（佛山）分解因式a 3-a 的结果是（ ）A ．a （a 2-1）B ．a （a-1）2C ．a （a+1）（a-1）D ．（a 2+a ）（a-1）6．（恩施州）把x 2y-2y 2x+y 3分解因式正确的是（ ）A ．y （x 2-2xy+y 2）B ．x 2y-y 2（2x-y ）C ．y （x-y ）2D ．y （x+y ）2二、填空题：7.（2019年威海）分解因式:2x 2－2x ＋＝ .8．（2019年淄博）分解因式：=++x x x 6523 ．A ．3x -6x=x （3x-6）B ．-a +b =（b+a ）（b-a ）C．4x2-y2=（4x+y）（4x-y）D．4x2-2xy+y2=（2x-y）233．（内江）若m-n=6，且m-n=2，则m+n= ．参考答案一、选择题：1-5 CDBDC 6 C二、填空题：6.答案：()221 12x-7.答案：()()32++xxx8.答案：m(x+y)(x-y)9.答案：m(m-5)10.答案：B11.答案：2)2 (-ba12.答案：x(2-x)(2+x)13. 答案：5(x+2)(x -2)14. 答案：m(m+2)(m -2)15. 答案：b(a+2b)(a -2b)17. 答案：-91(3x+1)(3x -1)16. 答案：3(a+2b)(a -2b)17. 答案：2x(x -2)18. 答案：2m(m+2)(m -2)19. 答案：2（a+2b ）(a -2b)20. 答案：22）（-x21. 答案：a(b+1)(b -1)22. 答案：(x -1)23. 答案：a(a -2)24. 答案：x(x+y)25. 答案：(a+3)(a -3)26. 答案：x -227. 答案：(x+y)(x -y)28. 答案：(x+3y)(x -3y)29. 答案：a(m+2n)(m -2n)30. 答案：))((22x y x y y x -+ 31. 答案：332. 答案：2433. 答案：x(x+1)(x -1)34. 答案：-31。

中考数学一轮复习 第1讲：实数概念与运算 一、夯实基础1、绝对值是6的数是________2、|21|-的倒数是________________。

3、2的平方根是_________.4、下列四个实数中，比－1小的数是（ ） A ．－2 B.0 C ．1 D ．25、在下列实数中,无理数是( )A.2B.0C.5D.13二、能力提升6、小明家冰箱冷冻室的温度为－5℃，调高4℃后的温度为（ ）A ．4℃B ．9℃C ．－1℃D ．－9℃7、定义一种运算☆，其规则为a ☆b =1a ＋1b，根据这个规则、计算2☆3的值是（ ）A ．65B ． 15C ．5D ．6 8、下列计算不正确的是（ ）（A ）31222-+=- （B ）21139⎛⎫-= ⎪⎝⎭ （C ）33-= （D ）1223= 三、课外拓展9、实数a 、b 在数轴上位置如图所示，则|a|、|b|的大小关系是________。

四、中考链接10、数轴上的点A 到原点的距离是6，则点A 表示的数为（ ）A. 6或6-B. 6 C . 6- D. 3或3-11、如果a与1互为相反数，则a等于（）．A．2 B．2- C．1 D．1-12、下列哪一选项的值介于0.2与0.3之间？（）A、 4.84B、0.484C、0.0484D、0.0048413、―2×63＝14、在﹣2，2，2这三个实数中，最小的是15、写出一个大于3且小于4的无理数。

参考答案一、夯实基础1、6和-62、2±3、24、A5、C二、能力提升6、C7、A8、A三、课外拓展9、a b>四、中考链接10、A11、C12、C13、-214、﹣215、解：∵π≈3.14…，∴3＜π＜4，故答案为：π（答案不唯一）．第2讲：整式与因式分解一、夯实基础1．计算（直接写出结果）①a ·a 3=③(b 3)4=④(2ab )3=⑤3x 2y ·)223y x -（= 2．计算：2332)()(a a -+-＝ ．3．计算：)(3)2(43222y x y x xy -⋅⋅-＝ ．4．1821684=⋅⋅n n n ，求n ＝ ．5．若._____34,992213=-=⋅⋅++-m m y x y x y x n n m m 则二、能力提升6．若)5)((-+x k x 的积中不含有x 的一次项，则k 的值是（）A ．0B ．5C ．－5D ．－5或57．若))(3(152n x x mx x ++=-+，则m 的值为（）A ．－5B ．5C ．－2D ．28．若142-=y x ，1327+=x y ，则y x -等于（）A ．－5B ．－3C ．－1D ．19．如果552=a ，443=b ，334=c ，那么（）A ．a ＞b ＞cB ．b ＞c ＞aC ．c ＞a ＞bD ．c ＞b ＞a三、课外拓展10．①已知,2,21==mn a 求n m a a )(2⋅的值.②若的求n n n x x x 22232)(4)3(,2---=值11．若0352=-+y x ，求y x 324⋅的值．四、中考链接12．（龙口）先化简，再求值：（每小题5分，共10分）（1）x （x -1）+2x （x +1）－（3x -1）（2x -5），其中x =2．（2）342)()(m m m -⋅-⋅-，其中m =2-13、（延庆）已知，求下列各式的值：（1）； （2）．14、（鞍山）已知：，.求：（1）；（2）.15、计算：；参考答案一、夯实基础1．a 4，b 4，8a 3b 3，-6x 5y 3；2．0；3．-12x 7y 9；4．2；5．4二、能力提升6．B ；7．C ；8．B ；9．B ；三、课外拓展10．①161；②56； 11．8；四、中考链接12．(1)-3x 2+18x-5，19；(2)m 9，-512；13.（1）45；（2）5714.（1）9；（2）115.第3讲：分式检测一、夯实基础1．下列式子是分式的是( )A ．x 2B ．x x ＋1C ．x 2＋yD ．x32．如果把分式2xy x ＋y 中的x 和y 都扩大3倍，那么分式的值( ) A ．扩大3倍 B ．缩小3倍 C ．扩大9倍 D ．不变3．当分式x －1x ＋2的值为0时，x 的值是( ) A ．0 B ．1 C ．－1 D ．－2 4．化简：(1)x 2－9x －3＝__________. (2)aa －1＋11－a＝__________. 二、能力提升5．若分式2a ＋1有意义，则a 的取值范围是( ) A ．a ＝0 B ．a ＝1 C ．a ≠－1 D ．a ≠06．化简2x 2－1÷1x －1的结果是( ) A ．.2x －1 B ．2x 3－1 C ．2x ＋1D ．2(x ＋1) 7．化简m 2－163m －12得__________；当m ＝－1时，原式的值为__________． 三、课外拓展8．化简⎝ ⎛⎭⎪⎫m 2m －2＋42－m ÷(m ＋2)的结果是( ) A ．0 B ．1 C ．－1 D ．(m ＋2)29．下列等式中，不成立的是( )A ．x 2－y 2x －y ＝x －yB ．x 2－2xy ＋y 2x －y＝x －yC ．xy x 2－xy ＝y x －yD ．y x －x y ＝y 2－x 2xy10．已知1a －1b ＝12，则aba －b 的值是( )A ．12 B ．－12 C ．2 D ．－211．当x ＝__________时，分式x －2x ＋2的值为零．12．计算（2-a a—2+a a）·a a 24-的结果是（ ）A ． 4B ． －4C ．2aD ．－2a13．分式方程2114339x x x +=-+-的解是（ ）A ．x=－2B ．x=2C ． x=±2D ．无解14．把分式(0)xyx y x y +≠+中的x ,y 都扩大3倍，那么分式的值（）A ．扩大为原来的3倍B ．缩小为原来的13C ．扩大为原来的9倍D ．不变四、中考链接15．(临沂)先化简，再求值：(1)⎝ ⎛⎭⎪⎫1－1a －1÷a 2－4a ＋4a 2－a ，其中a ＝－1.(2)3－x 2x －4÷⎝ ⎛⎭⎪⎫5x －2－x －2，其中x ＝3－3.参考答案 一、夯实基础 1．B B 项分母中含有字母． 2．A 因为x 和y 都扩大3倍，则2xy 扩大9倍，x ＋y 扩大3倍，所以2xy x ＋y 扩大3倍．3．B 由题意得x －1＝0且x ＋2≠0，解得x ＝1.4．(1)x ＋3 (2)1 (1)原式＝(x ＋3)(x －3)x －3＝x ＋3；(2)原式＝a a －1－1a －1＝a －1a －1＝1. 二、能力提升5．C 因为分式有意义，则a ＋1≠0，所以a ≠－1.6．C 原式＝2(x ＋1)(x －1)·(x －1)＝2x ＋1. 7．m ＋43 1 原式＝(m ＋4)(m －4)3(m －4)＝m ＋43.当m ＝－1时，原式＝－1＋43＝1. 三、课外拓展8．B 原式＝m 2－4m －2·1m ＋2＝(m ＋2)(m －2)m －2·1m ＋2＝1. 9．A x 2－y 2x －y ＝(x ＋y )(x －y )x －y＝x ＋y . 10．D 因为1a －1b ＝12，所以b －a ab ＝12，所以ab ＝－2(a －b )，所以ab a －b ＝－2(a －b )a －b＝－2.11．2 由题意得x －2＝0且x ＋2≠0，解得x ＝2.12. B13. B14. A四、中考链接15．解：(1)⎝⎛⎭⎪⎫1－1a －1÷a 2－4a ＋4a 2－a ＝a －2a －1·a (a －1)(a －2)2＝a a －2.当a ＝－1时，原式＝aa －2＝－1－1－2＝13.(2)3－x2x－4÷⎝⎛⎭⎪⎫5x－2－x－2＝3－x2(x－2)÷⎝⎛⎭⎪⎫5x－2－x2－4x－2＝3－x2(x－2)÷9－x2x－2＝3－x2(x－2)·x－2(3－x)(3＋x)＝12x＋6.∵x＝3－3，∴原式＝12x＋6＝36.第4讲：二次根式一、夯实基础1．使3x －1有意义的x 的取值范围是( )A ．x ＞13B ．x ＞－13C ．x ≥13D ．x ≥－132．已知y ＝2x －5＋5－2x －3，则2xy 的值为( ) A ．－15 B ．15 C ．－152 D ．1523．下列二次根式中，与3是同类二次根式的是( ) A ．18 B ．27 C ．23D ．324．下列运算正确的是( )A ．25＝±5B ．43－27＝1C ．18÷2＝9D ．24·32＝6 5．估计11的值( )A ．在2到3之间B ．在3到4之间C ．在4到5之间D ．在5到6之间 二、能力提升6．若x ，y 为实数，且满足|x －3|＋y ＋3＝0，则⎝ ⎛⎭⎪⎫x y 2 012的值是__________．7．有下列计算：①(m 2)3＝m 6，②4a 2－4a ＋1＝2a －1，③m 6÷m 2＝m 3，④27×50÷6＝15，⑤212－23＋348＝143，其中正确的运算有__________．(填序号)三、课外拓展8．若x ＋1＋(y －2 012)2＝0，则x y ＝__________. 9．当－1＜x ＜3时，化简：x －32＋x 2＋2x ＋1＝__________.10．如果代数式4x －3有意义，则x 的取值范围是________．11、比较大小：⑴3 5 2 6 ⑵11 －10 14 －1312、若最简根式m2－3 与5m+3 是同类二次根式，则m= .13、若 5 的整数部分是a，小数部分是b，则a－1b= 。

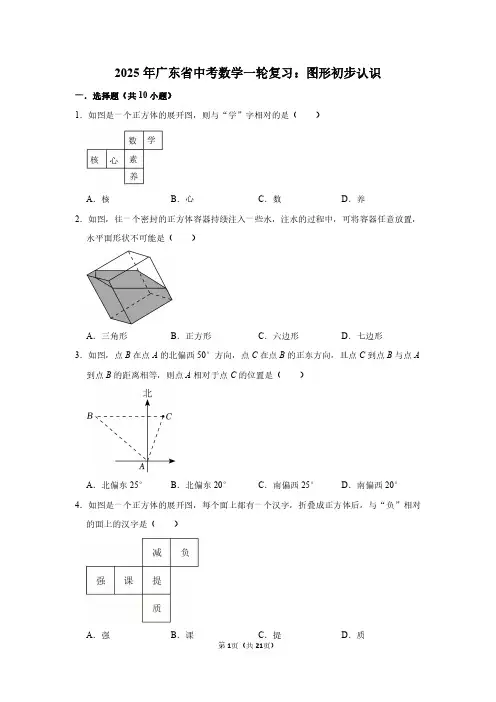
第1页（共21页）2025年广东省中考数学一轮复习：图形初步认识
一．选择题（共10小题）
1．如图是一个正方体的展开图，则与“学”字相对的是（
）
A ．核
B ．心
C ．数
D ．养
2．如图，往一个密封的正方体容器持续注入一些水，注水的过程中，可将容器任意放置，水平面形状不可能是（
）
A ．三角形
B ．正方形
C ．六边形
D ．七边形
3．如图，点B 在点A 的北偏西50°方向，点C 在点B 的正东方向，且点C 到点B 与点A 到点B 的距离相等，则点A 相对于点C 的位置是（
）
A ．北偏东25°
B ．北偏东20°
C ．南偏西25°
D ．南偏西20°
4．如图是一个正方体的展开图，每个面上都有一个汉字，折叠成正方体后，与“负”相对的面上的汉字是（
）
A ．强
B ．课
C ．提
D ．质。

[初中数学]中考数学一轮复习第1-22讲教案+导学案+精练(66套)-人教版44第2讲:整式与因式分解一、复习目标1、在识记整式和因式分解知识点的基础上理解并能熟练的应用整式和因式分解知识点。

2、能结合具体情境创造性的综合应用因式分解解决问题。

二、课时安排1课时三、复习重难点1、分解因式及利用因式分解法解决问题。

2、整式的合并及变形计算。

四、教学过程(一)知识梳理整式的有关概念单项式定义：数与字母的________的代数式叫做单项式，单独的一个________或一个________也是单项式单项式次数：一个单项式中，所有字母的________ 叫做这个单项式的次数单项式系数：单项式中的叫做单项式的系数多项式定义：几个单项式的________叫做多项式积的乘方，等于把积的每一个因式分别乘方，再把所得的幂相乘．即：(ab)n＝________(n为整数) 同底数幂相除，底数不变，指数相减. 即：a m÷a n ＝________(a≠0，m、n都为整数)整式的乘法：单项式与单项式相乘，把它们的分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式单项式与多项式相乘，就是用单项式去乘多项式的每一项，再把所得的积相加，即m(a＋b＋c)＝多项式与多项式相乘，先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加，即(m ＋n)(a＋b)＝整式的除法：单项式除以单项式，与分别相除，作为商的因式，对于只在被除式里含有的字母，则连同它的指数作为商的一个因式多项式除以单项式，先把这个多项式的每一项分别这个单项式，然后把所得的商相加乘法公式：平方差公式：(a＋b)(a－b)＝________完全平方公式：(a±b)2＝________常用恒等变换：(1)a2＋b2＝____________＝____________(2)(a－b)2＝(a＋b)2－因式分解的相关概念及分解基本方法公因式定义：一个多项式各项都含有的的因式，叫做这个多项式各项的公因式提取公因式法定义：一般地，如果多项式的各项都有公因式，可以把这个公因式提到括号外面，将多项式写成因式的乘积形式，即ma＋mb＋mc＝________运用公式法：平方差公式a2－b2＝___________完全平方公式a2＋2ab＋b2＝________ ，a2－2ab ＋b2＝________二次三项式x2+(p+q)x+pq=________（二）题型、方法归纳考点一整式的有关概念技巧归纳：注意单项式次数、单项式系数的概念考点二同类项、合并同类项技巧归纳：(1)同类项必须符合两个条件：第一所含字母相同，第二相同字母的指数相同，两者缺一不可．(2)根据同类项概念——相同字母的指数相同列方程(组)是解此类题的一般方法．考点三整式的运算技巧归纳：(1)进行整式的运算时，一要注意合理选择幂的运算法则，二要注意结果的符号． (2)不要把同底数幂的乘法和整式的加减法混淆 (3)单项式的除法关键：注意区别“系数相除”与“同底数幂相除”的含义，一定不能把同底数幂的指数相除．（4）整式的运算顺序是：先计算乘除，再做整式的加减，整式加减的实质就是合并同类项，其中能运用乘法公式计算的应采用乘法公式进行计算．考点四因式分解的相关概念及分解基本方法技巧归纳：(1)因式分解时有公因式的要先提取公因式，再考虑是否应用公式法或其他方法继续分解．(2)提公因式时，若括号内合并的项有公因式应再次提取；注意符号的变换(3)应用公式法因式分解时，要牢记平方差公式和完全平方式及其特点．(4)因式分解要分解到每一个多项式不能再分解为止．（三）典例精讲1、如果□×3ab=3a2b，则□内应填的代数式是（）A.abB.3abC.aD.3a答案：C2、在下列代数式中，次数为3的单项式是( )A．xy2 B．x3－y3C．x3y D．3xy[解析]由单项式次数的概念可知次数为3的单项式是xy2. 所以本题选项为A.3、如果单项式231123ba y yx x与是同类项，那么a，b的值分别为( )A．2，2 B．－3，2 C．2，3 D．3，2[解析] 依题意知两个单项式是同类项，根据相同字母的指数相同列方程，得 D点析：(1)同类项必须符合两个条件：第一所含字母相同，第二相同字母的指数相同，两者缺一不可．(2)根据同类项概念——相同字母的指数相同列方程(组)是解此类题的一般方法．4、下列运算中，正确的是( )A．a2·a3＝a6 B．a3÷a2＝aC．(a3)2＝a9 D．a2＋a2＝ a5[解析]因为a2·a3＝a2＋3＝a5，a3÷a2＝a3－2＝a，(a3)2＝a3×2＝a6，a2＋a2＝ 2a2.故选B.点析：(1)进行整式的运算时，一要注意合理选择幂的运算法则，二要注意结果的符号．(2)不要把同底数幂的乘法和整式的加减法混淆，如a3·a5 ＝a8和a3＋a3＝2a3. (a m)n和a n·a m也容易混淆．(3)单项式的除法关键：注意区别“系数相除”与“同底数幂相除”的含义，如6a5÷3a2＝(6÷3)a5－2＝2a3, 一定不能把同底数幂的指数相除．5、先化简，再求值：(2x＋3)(2x－3)－4x(x－1)＋(x－2)2，其中x ＝－3[解析] 按运算法则化简代数式，再代入求值．解：原式＝4x2－9－4x2＋4x＋x2－4x＋4＝x2－5，当x＝－3时，原式＝(－)2－5＝3－5＝－2.点析：整式的运算顺序是：先计算乘除，再做整式的加减，整式加减的实质就是合并同类项，其中能运用乘法公式计算的应采用乘法公式进行计算．6、分解因式(x－1)2－2(x－1)＋1的结果是( )A．(x－1)(x－2) B. x2 C．(x＋1)2D. (x－2)2[解析] 首先把x－1看做一个整体，观察发现符合完全平方公式，直接利用完全平方公式进行分解．(x－1)2－2(x－1)＋1＝(x－1－1)2＝(x－2)2.点析： (1)因式分解时有公因式的要先提取公因式，再考虑是否应用公式法或其他方法继续分解．(2)提公因式时，若括号内合并的项有公因式应再次提取；注意符号的变换y－x＝－(x－y)，(y－x)2＝(x－y)2.(3)应用公式法因式分解时，要牢记平方差公式和完全平方式及其特点．(4)因式分解要分解到每一个多项式不能再分解为止．7、①是一个长为2m，宽为2n(m>n)的长方形，用剪刀沿图中虚线(对称轴)剪开，把它分成四块形状和大小都一样的小长方形，然后按图3－1②那样拼成一个正方形，则中间空的部分的面积是( ) A．2mn B．(m＋n)2 C．(m－n)2 D．m2－n2[解析] 中间空的部分的面积是(m＋n)2－2m·2n＝(m＋n)2－4mn＝(m－n)2.点析：(1)通过拼图的方法可验证平方差公式和完全平方公式，关键要能准确计算阴影部分的面积．(2)利用因式分解进行计算与化简，先把要求的代数式进行因式分解，再代入已知条件计算．（四）归纳小结本部分内容要求熟练掌握整式、同类项、合并同类项的有关概念及整式的运算、因式分解的相关概念及分解基本方法。

2020届中考数学一轮复习讲义考点三十八：与圆有关的概念聚焦考点☆温习理解1、圆的定义在一个个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A随之旋转所形成的图形叫做圆，固定的端点O叫做圆心，线段OA叫做半径。

2、弦连接圆上任意两点的线段叫做弦。

(如图中的AB)3.直径经过圆心的弦叫做直径。

(如图中的CD)直径等于半径的2倍。

4.半圆圆的任意一条直径的两个端点分圆成两条弧，每一条弧都叫做半圆。

5.弧、优弧、劣弧圆上任意两点间的部分叫做圆弧，简称弧。

弧用符号“⌒”表示，以A，B为端点的弧记作“”，读作“圆弧AB”或“弧AB”。

大于半圆的弧叫做优弧(多用三个字母表示)；小于半圆的弧叫做劣弧(多用两个字母表示)5、垂径定理及其推论垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧。

推论1：(1)平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧。

(2)弦的垂直平分线经过圆心，并且平分弦所对的两条弧。

(3)平分弦所对的一条弧的直径垂直平分弦，并且平分弦所对的另一条弧。

推论2：圆的两条平行弦所夹的弧相等。

6、圆的对称性1、圆的轴对称性圆是轴对称图形，经过圆心的每一条直线都是它的对称轴。

2、圆的中心对称性圆是以圆心为对称中心的中心对称图形。

3、弦心距从圆心到弦的距离叫做弦心距。

名师点睛☆典例分类考点典例一、垂径定理【例1】(2019•广西北部湾经济区•3分)《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著，与古希腊的《几何原本》并称现代数学的两大源泉．在《九章算术》中记载有一问题“今有圆材埋在壁中，不知大小．以锯锯之，深一寸，锯道长一尺，问径几何？”小辉同学根据原文题意，画出圆材截面图如图所示，已知：锯口深为1寸，锯道AB=1尺(1尺=10寸)，则该圆材的直径为______寸．【答案】26【解析】解：设⊙O的半径为r．在Rt△ADO中，AD=5，OD=r-1，OA=r，则有r2=52+(r-1)2，解得r=13，∴⊙O的直径为26寸，故答案为：26．设⊙O的半径为r．在Rt△ADO中，AD=5，OD=r-1，OA=r，则有r2=52+(r-1)2，解方程即可．本题考查垂径定理、勾股定理等知识，解题的关键是学会利用参数构建方程解决问题，属于中考常考题型．【举一反三】(2018年湖北省黄梅濯港镇中心学校数学中考模拟)关于圆的性质有以下四个判断：①垂直于弦的直径平分弦，②平分弦的直径垂直于弦，③在同圆或等圆中，相等的弦所对的圆周角相等，④在同圆或等圆中，相等的圆周角所对的弦相等，则四个判断中正确的是()A. ①③B. ②③C. ①④D. ②④【答案】C【解析】垂直于弦的直径平分弦，所以①正确；平分弦(非直径)的直径垂直于弦，所以②错误；在同圆或等圆中，相等的弦所对的圆周角相等或互补，所以③错误；在同圆或等圆中，相等的圆周角所对的弦相等，所以④正确．故选：C．点睛：本题考查了圆周角定理：在同圆或等圆中，同弧所对的圆周角线段，都等于这条弧所对的圆心角的一半.推论：半圆(或直径)所对的圆周角是直角，90°的圆周角所对的弦是直径.考点典例二、求弦心距【例2】(2018贵州黔东南中考模拟)小颖同学在手工制作中，把一个边长为12cm的等边三角形纸片贴到一个圆形的纸片上，若三角形的三个顶点恰好都在这个圆上，则圆的半径为()A．23cm B．43cm C．63cm D．83cm【答案】B．考点：三角形的外接圆与外心；等边三角形的性质．【点睛】作出几何图形，再由外接圆半径、边心距和边长的一半组成的三角形中，已知外接圆半径和特殊角，可求得边心距．考查了等边三角形的性质．注意：等边三角形的外接圆和内切圆是同心圆，圆心到顶点的距离等于外接圆半径，边心距等于内切圆半径． 【举一反三】如图，半径为5的⊙A 中，弦B C ，ED 所对的圆心角分别是∠BAC ，∠EAD. 已知DE=6，∠BAC+∠EAD=180°，则弦BC 的弦心距等于( )A.241B. 234C. 4D. 3 【答案】D ．考点：1.圆周角定理；2.全等三角形的判定和性质；3.垂径定理；4.三角形中位线定理. 【分析】如答图，过点A 作AH ⊥BC 于H ，作直径CF ，连接BF ，∵∠BAC+∠EAD=180°，∠BAC+∠BAF=180°， ∴∠DAE=∠BAF.在△ADE 和△ABF 中，∵AD ABDAE BAF AE AF =⎧⎪∠=∠⎨⎪=⎩，∴△ADE≌△ABF(SAS).∴DE=BF=6. ∵AH⊥BC，∴CH=BH.又∵CA=AF，∴AH为△CBF的中位线. ∴AH=12BF=3．故选D．考点典例三、最短路线问题【例3】(2019年黄冈市中考模拟)如图，MN是半径为1的⊙O的直径，点A在⊙O上，∠AMN=30°，点B 为劣弧AN的中点．点P是直径MN上一动点，则PA+PB的最小值为()A．B．1 C． 2 D． 2【答案】A.【解析】作点B关于MN的对称点B′，连接OA、OB、OB′、AB′，则AB′与MN的交点即为PA+PB的最小时的点，PA+PB的最小值=AB′，∵∠AMN=30°，∴∠AON=2∠AMN=2×30°=60°，∵点B为劣弧AN的中点，∴∠BON=12∠AON=12×60°=30°，由对称性，∠B′ON=∠BON=30°，∴∠AOB′=∠AON+∠B′ON=60°+30°=90°，∴△AOB′是等腰直角三角形，∴22×2，即PA+PB的最小值2．故选A．【点睛】本题考查了轴对称确定最短路线问题，在同圆或等圆中，同弧所对的圆心角等于圆周角的2倍的性质，作辅助线并得到△AOB′是等腰直角三角形是解题的关键． 【举一反三】(2018浙江温州中考模拟)如图，在△ABC 中，AB =10，AC =8，BC =6，以边AB 的中点O 为圆心，作半圆与AC 相切，点P ，Q 分别是边BC 和半圆上的动点，连接PQ ，则PQ 长的最大值与最小值的和是( )A ． 6B ． 1132C ． 9D ． 332【答案】C ． 【解析】试题分析：如图，设⊙O 与AC 相切于点E ，连接OE ，作OP 1⊥BC 垂足为P 1交⊙O 于Q 1，此时垂线段OP 1最短，P 1Q 1最小值为OP 1﹣OQ 1，∵AB =10，AC =8，BC =6，∴AB 2=AC 2+BC 2，∴∠C =90°，∵∠OP 1B =90°，∴OP 1∥AC∵AO =OB ，∴P 1C =P 1B ，∴OP 1=12AC =4，∴P 1Q 1最小值为OP 1﹣OQ 1=1，如图，当Q 2在AB 边上时，P 2与B 重合时，P 2Q 2最大值=5+3=8，∴PQ 长的最大值与最小值的和是9．故选C ．考点：切线的性质；最值问题．课时作业☆能力提升一．选择题1．(山东省济南市长清区2018届九年级3月质量(模拟)检测数学试题)如图，直径为10的A 经过点C 和点O ，点B 是y 轴右侧A 优弧上一点，∠OBC=30°，则点C 的坐标为( )A. ()0,5B. ()0,53 C. 50,32⎛⎫⎪⎝⎭ D. 50,33⎛⎫⎪⎝⎭【答案】A故选A ．点睛：此题考查了圆周角定理与含30°角的直角三角形的性质．此题难度适中，注意掌握辅助线的作法是解此题的关键，注意数形结合思想的应用．2. 如图，AB 为⊙O 的直径，CD 是⊙O 的弦，∠ADC=35°，则∠CAB 的度数为( )A. 35°B. 45°C. 55°D. 65° 【来源】江苏省盐城市2018年中考数学试题【答案】C点睛：本题考查了同弧所对的圆周角相等以及直径所对的圆周角是直角等知识.3.已知⊙O 的直径CD=10cm ，AB 是⊙O 的弦，AB ⊥CD ，垂足为M ，且AB=8cm ，则AC 的长为( ) A. 25cm B. 45cm C. 25cm 或45cm D.5 23cm 或43cm 【答案】C ． 【解析】试题分析：根据题意画出图形，由于点C 的位置不能确定，故应分两种情况进行讨论 连接AC ，AO ，∵⊙O 的直径CD=10cm ，AB ⊥CD ，AB=8cm ，∴AM=12AB=12×8=4cm ，OD=OC=5cm. 当C 点位置如答图1所示时，∵OA=5cm ，AM=4cm ，CD ⊥AB ，∴2222OM OA AM 543=-=-=cm.∴CM=OC+OM=5+3=8cm. ∴在Rt △AMC 中，2222AC AM CM 4845=+=+=cm. 当C 点位置如图2所示时，同理可得OM=3cm ， ∵OC=5cm ，∴MC=5﹣3=2cm.∴在Rt △AMC 中，2222AC AM CM 4225=+=+=． 综上所述，AC 的长为25cm 或45cm . 故选C ．考点：1.垂径定理；2.勾股定理；3.分类思想的应用．4. (2019•黄冈)如图，一条公路的转弯处是一段圆弧(AB)，点O是这段弧所在圆的圆心，AB=40 m，点C是AB的中点，且CD=10 m，则这段弯路所在圆的半径为A．25 m B．24 m C．30 m D．60 m【答案】A【解析】∵OC⊥AB，∴AD=DB=20 m，在Rt△AOD中，OA2=OD2+AD2，设半径为r得：r2=(r-10)2+202，解得r=25 m，∴这段弯路的半径为25 m，故选A．5. 如图，MN是⊙O的直径，点A是半圆上的三等分点，点B是劣弧AN的中点，点P是直径MN上一动点．若MN=22，则PA+PB的最小值是()A．22B．2C．1 D．2【答案】D.6. (西藏拉萨北京实验中学等四校2018届九年级第一次联考数学试题)如图，△ABC为⊙O的内接三角形，∠BOC=80°，则∠A等于()A. 80B. 60C. 50D. 40【答案】D【解析】试题解析：由圆周角定理得,1402A BOC∠=∠=，故选D.点睛：在同圆或等圆中，同弧或等弧所对的圆周角等于圆心角的一半.学&科网二．填空题7.(安徽省合肥市2018届九年级第五次十校联考)如图，⊙O是△ABC的外接圆，∠BAC=120°，若⊙O的半径为2，则弦BC的长为__________．【答案】23．∵四边形ABEC 是圆内接四边形, 120BAC ∠=，60E ∴∠=，120BOC ∴∠=，又∵OD ⊥BC ，602BOD BC BD ∴∠==，，3sin60232BD OB ∴=⨯=⨯=， 22 3.BC BD ∴==故答案为： 2 3.点睛:圆内接四边形的对角互补.8. (新疆乌鲁木齐市第九十八中学2018届九年级下学期第一次模拟考试)如图，△ABC 是⊙O 的内接锐角三角形，连接AO ，设∠OAB=α，∠C=β，则α+β=______°。