第11章 主成分和因子分析
- 格式:ppt
- 大小:657.50 KB
- 文档页数:65


第十一章 多元分析:主成分分析与因子分析引言主成分分析和因子分析在多元分析框架内是数据结构分析技术,与第六章的多元回归、第七章的多变量协整一起是多变量分析中广泛使用的技术。
它们不同于多元回归。
回归的目标是识别外生变量与内生变量的关系,而在主成分分析和因子分析情形下,仅确定内生变量间的结构关系。
它们也不像协整,变量间不需要平稳性。
在金融、社会科学或其它领域,通常需要识别多变量结构的特征,其有两个特征是被子广泛关心的:1. 多变量结构中的波动性。
2. 变量间的相关或共线性。
在结构的整体变化中,通常是一些变量起产生主要的影响,而其它变量仅有次要的或不显著的影响。
困难的是要了解哪些变量能被确定在这个结构中和它在结构中应怎样度量。
例如,如果两个变量是完全相关的,则不需要第二个变量,它不会带来进一步的信息。
这类似多元回归的共线问题。
在一般情况下,包含哪个变量,剔除哪个变量并不是很清楚的,我们需要有能够程序化的有效方法来识别带有最可用信息的变量或变量组合。
主成分分析(PCA )是分析多变量结构波动时有用的技术。
因子分析(F A )在分析多变量结构变量的相关时很有用。
两者都依赖于方差/协方差矩阵,因为这个矩阵在一定范围内包含了变量间有用的全部信息。
因此在一定范围内,两者是重复的或相互补充的。
在这章,我们将方差/协方差矩阵记为C 。
尽管PCA 和F A 都利用方差/协方差矩阵,但它们不同于第四章和第九章中的均值—方差分析。
均值—方差分析度量了一组变量的总体变异性,而没有特别指明一部分变量对总变异性的贡献。
PCA 识别和排序了部分变量在总变异性中的贡献,每个部分变量称为“主成分”。
它识别了部分变量间组成的协方差的强度,每个主成分对总的变异性的贡献,并根据部分变量组的方差进行排序。
使用PCA ,数据内的总体变异性由特征值之和(它等于C矩阵主对角线上元素之和,也称为迹)度量,成分(变量的线性组合)的选择是依次序减少特征值,直到满足总变异性的一个足够大的比例。


主成分分析和因子分析
习题答案
SANY标准化小组 #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#
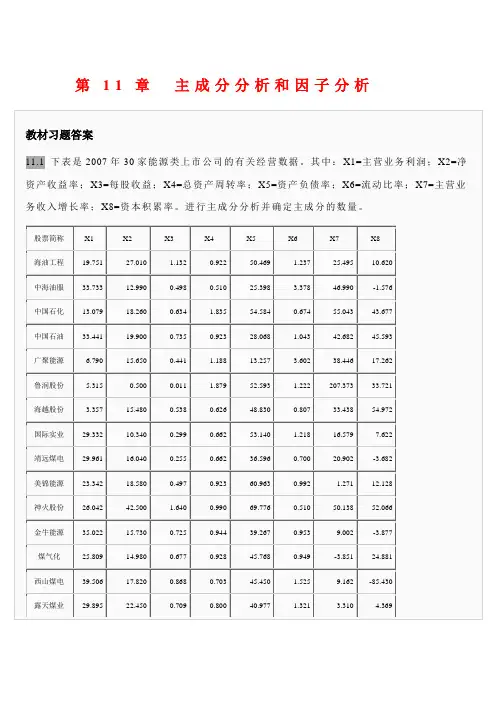
第11章主成分分析和因子分析
司盈利能力有关,因此可命名为“盈利能力”。
因子2 与X5(资产负债率)、X6(流动比率)X8(资本积累率)这3个变量的载荷系数较大,这三个变量主要涉及企业的偿债能力,因此可命为“偿债能力因子”。
因子3与X1(主营业务利润)、 X4(总资产周转率)、X7(主营业务收增长率)这三个变量的载荷系数较大,这三个变量分别涉及了盈利能力、资产管理水平、企业成能力等,因此,这个因子的命名比较困难。
各公所的因子综合得分和排名如下:
对下表中的50名学生成绩进行主成分分析,可以选择几个综合变量来代表这些学生的六门课程绩
学生代码数学物理化学语文历史英语
1716494526152
2789681808976
3695667759480
4779080686660
5846775607063
6626783718577。



数据分析中的因子分析和主成分分析在数据分析领域,因子分析和主成分分析是两种常用的多变量分析方法。
它们可以用来处理大量的数据,找出数据的内在规律,并将数据简化为更少的变量。
本文将介绍因子分析和主成分分析的定义、应用以及它们在数据分析中的区别和联系。
一、因子分析因子分析是一种用于研究多个变量之间的潜在因素结构及其影响的统计方法。
它通过将多个观测变量转化为少数几个无关的因子,来解释变量之间的相关性。
因子分析的基本思想是将多个相关观测变量归因于少数几个潜在因子,这些潜在因子不能被观测到,但可以通过观测变量的变化来间接地推断出来。
因子分析通常包括两个主要步骤:提取因子和旋转因子。
提取因子是指确定能够解释原始变量方差的主要共性因子,常用的方法有主成分分析法和最大似然估计法。
旋转因子是为了减少因子之间的相关性,使得因子更易于解释。
常用的旋转方法有正交旋转和斜交旋转。
因子分析的应用非常广泛,可以用于市场研究、社会科学调查、心理学、金融等领域。
例如,在市场研究中,因子分析可以用来确定消费者购买行为背后的潜在因素,从而更好地理解市场需求。
二、主成分分析主成分分析是一种通过线性变换将原始变量转化为一组线性无关的主成分的统计方法。
主成分是原始变量的线性组合,具有较大的方差,能够尽可能多地解释原始数据。
主成分分析的主要思想是将原始变量投影到一个新的坐标系中,使得新坐标系上的第一主成分具有最大方差,第二主成分具有次最大方差,以此类推。
通过选择解释原始数据方差较多的前几个主成分,我们可以实现数据的降维和主要信息提取。
主成分分析在数据降维、特征提取和数据可视化等领域有广泛的应用。
例如,在图像处理中,主成分分析可以用来压缩图像数据、提取重要特征,并且可以在保留图像主要信息的同时减少存储空间的需求。
三、因子分析和主成分分析的区别和联系因子分析和主成分分析在某些方面有相似之处,但也存在明显的区别。
首先,因子分析是用于研究多个观测变量之间的潜在因素结构,而主成分分析是通过线性变换将原始变量转化为一组线性无关的主成分。

主成分分析和因子分析法一、主成分分析概论主成分分析的工作对象是样本点×定量变量类型的数据表。
它的工作目标,就是要对这种多变量的平面数据表进行最佳综合简化。
也就是说,要在力保数据信息丢失最少的原则下,对高维变量空间进行降维处理。
很显然,识辨系统在一个低维空间要比一个高维空间容易得多。
英国统计学家斯格特(M.Scott )在1961年对157个英国城镇发展水平进行调查时,原始测量的变量有57个。
而通过主成分分析发现,只需5个新的综合变量(它们是原变量的线性组合),就可以95%的精度表示原数据的变异情况,这样,对问题的研究一下子从57维降到5维。
可以想象,在5维空间中对系统进行任何分析,都比在57维中更加快捷、有效。
另一项十分著名的工作是美国的统计学家斯通(Stone)在1947年关于国民经济的研究。
他曾利用美国1929~1938年各年的数据,得到了17个反映国民收入与支出的变量要素,例如雇主补贴、消费资料和生产资料、纯公共支出、净增库存、股息、利息和外贸平衡等等。
在进行主成分分析后,竟以97.4%的精度,用三个新变量就取代了原17个变量。
根据经济学知识,斯通给这三个新变量要别命名为总收入1F 、总收入变化率2F 和经济发展或衰退的趋势3F (是时间t 的线性项)。
更有意思的是,这三个变量其实都是可以直接测量的。
二、主成分分析的基本思想与理论1、主成分分析的基本思想在对某一事物进行实证研究中,为了更全面、准确地反映出事物的特征及其发展规律,人们往往要考虑与其有关系的多个指标,这些指标在多元统计中也称为变量。
这样就产生了如下问题:一方面人们为了避免遗漏重要的信息而考虑尽可能多的指标,而另一方面随着考虑指标的增多增加了问题的复杂性,同时也由于各指标均是对同一事物的反映,不可避免地造成信息的大量重叠,这种信息有时甚至会抹杀事物的真正特征与内在规律。
基于上述问题,人们就希望在定量研究中涉及的变量较少,而得到的信息量又较多。

因子分析与主成分分析因子分析和主成分分析是统计学中常用的降维技术,它们在数据分析和模式识别等领域中广泛应用。
本文将介绍因子分析和主成分分析的基本概念与原理,并对它们的应用进行探讨。
一、因子分析的概念与原理因子分析是一种用于发掘多个变量之间潜在关联性的方法。
当我们面对大量变量时,往往希望找到其中的共性因素来解释观测数据。
因子分析通过将变量进行降维,将原始变量解释为共同的因子或构念,从而减少信息冗余,提取数据的主要特征。
因子分析的核心思想是假设多个观测变量是由少数几个潜在因子所共同决定的。
这些潜在因子无法直接观测,但可以通过观测变量的线性组合进行间接估计。
通过因子分析,我们可以得到因子载荷矩阵,它描述了每个观测变量与潜在因子之间的关系强度。
二、主成分分析的概念与原理主成分分析是一种常用的无监督学习方法,用于降维和数据压缩。
与因子分析类似,主成分分析也采用线性组合的方式将原始变量映射到一个低维的特征空间。
主成分分析的目标是找到一组新的变量,称为主成分,它们能够最大程度地保留原始数据中的信息。
主成分分析的步骤如下:1. 标准化数据:将原始数据标准化,使得变量的均值为0,方差为1,以消除变量尺度差异的影响。
2. 计算协方差矩阵:计算标准化后的数据的协方差矩阵,用于评估各个变量之间的相关性。
3. 特征值分解:对协方差矩阵进行特征值分解,得到特征值和特征向量。
4. 选择主成分:根据特征值大小,选择要保留的主成分数量。
5. 计算主成分:将原始数据投影到所选择的主成分上,得到降维后的数据。
三、因子分析与主成分分析的应用1. 数据降维:因子分析和主成分分析可以用于降低数据集的维度,减少冗余信息。
在机器学习和数据挖掘中,高维数据集的处理往往会面临计算复杂度和过拟合等问题,降维技术可以有效解决这些问题。
2. 变量选择:通过因子分析和主成分分析,可以识别出对观测数据具有重要影响的变量。
这对于特征选择和模型建立有重要意义,可以提高模型的解释性和泛化能力。
第十一章因子分析地理模型因子分析因子分析的主要应用1、寻求基本结构、简化观测系统给定一组变量或观测数据,我们要问,变量的维数是否一定需要这么多,是否存在一个子集,特别是一个加权子集,来解释整个问题。
通常采用因子分析法将为数不多的变量减少为几个新因子,以再现它们之间的内在联系。
2、用于分类,将变量或样本进行分类,根据因子得分值,在因子轴所构成的空间中进行分类处理。
因子分析与主成分分析的区别第一节因子分析法的数学模型因子分析的结果完全的因子解因子分析的基本问题是用变量之间的相关系数来决定因子载荷。
因子模型的求解过程如下:设原始数据矩阵为:X =p表示变量数,n表示样本数。
将原始数据进行标准化变换:x ij-x ix ij’=(I=1,2,…p;j=1,2,…n)经标准化变换后的数据,其均值为0,方差为1,这样相关矩阵R和协方差矩阵S完全一样,这里相关矩阵:R=X*X’(为方便计,假定标准化处理后的矩阵仍记为X)。
求解R矩阵的特征方程|R=λI|=0,记特征值为λ1>λ2…>λp>=0,特征向量矩阵为U,这样有关系:R=U U’U为正交矩阵,并且满足U’U=UU’=I令F=U’X,则得FF’=F为主因子阵,并且Fα=U’Xα(α=1,2…n),即每一个Fα为第α个样品主因子观测值。
在因子分析中,通常只选m(m<p)其中主因子。
根据变量的相关选出第一主因子F1,使其在各变量的公共因子方差中所占的方差贡献最大。
R型的因子模型为X1=α11F1+α12F2+…+α1m F m +α1ε 1 X2=α21F1+α22F2+…+α2m F m +α2ε 2 … …X P=αP1F1+αP2F2+…+αPm F m +αmεm在因子模型中2、αij叫因子载荷,它是第I个变量在第j个主因子上的负荷,或者叫第I个变量在第j 个主因子上的权,它反映了第I个变量在第j个主因子上的相对重要性。
如果把x i看成m 维因子空间上的一个向量,则αij表示x i在坐标轴F j上的投影。
因子分析与主成分分析的区别与应用因子分析与主成分分析是统计学中常用的多变量分析方法,用于降维和提取数据中的主要信息。
虽然它们都可以用于数据分析,但在方法和应用上存在一些区别。
本文将介绍因子分析与主成分分析的区别,并讨论它们各自的应用。
一、因子分析与主成分分析的定义因子分析是一种用于研究多个观测变量之间的内在相关性结构的统计技术。
它通过将多个变量组合为少数几个“因子”来解释数据的方差。
每个因子代表一组相关性高的变量,可以帮助我们理解数据背后的潜在结构。
主成分分析是一种通过将原始变量转换为线性组合(即主成分)来降低多维数据维度的技术。
它通过找到数据中的最大方差方向来确定主成分,并逐步提取主成分,以解释数据的最大方差。
主成分分析可以帮助我们发现数据中的主要特征。
二、因子分析与主成分分析的区别1. 目的不同:因子分析的目的是确定一组能够最好地描述观测数据之间关系的因子,并解释数据中的方差。
因子分析更加关注变量之间的共同性和相关性,希望通过较少的因子来解释数据。
主成分分析的目的是通过寻找数据中的主要结构和主要特征来降低数据的维度。
主成分分析着重于方差的解释,通过线性组合来减少变量数量,提取出主要成分。
2. 基本假设不同:因子分析基于观察变量之间的共同性,假设观测变量是由一组潜在因子决定的。
它假设每个观测变量都与每个因子有一个固定的因子载荷。
主成分分析假设原始变量之间是线性相关的,并且通过线性变换,可以找到解释大部分数据方差的新变量。
3. 输出结果不同:因子分析输出因子载荷矩阵,该矩阵显示每个因子与每个观测变量之间的关系。
因子载荷表示每个因子对每个变量的贡献程度,可用于解释观测变量之间的共同性。
主成分分析输出的是主成分,每个主成分是原始变量的线性组合。
主成分按照解释的方差大小排序,因此前几个主成分更能代表原始数据的方差。
三、因子分析与主成分分析的应用因子分析的应用广泛,可以用于心理学、社会科学、市场调研等领域。
主成分分析和因子分析1.对原始数据进行标准化,使得每个特征的均值为0,标准差为12.计算数据集的协方差矩阵。
3.对协方差矩阵进行特征值分解,得到特征值和特征向量。
4.对特征值进行降序排列,并选择最大的k个特征值对应的特征向量作为主成分。
5.计算每个样本在选定的主成分上的投影值,得到降维后的数据集。
主成分分析的应用非常广泛。
它可以用于数据可视化、降维和特征选择。
主成分分析可以帮助我们发现数据中的模式和结构,找到最相关和最有信息的特征,并减少不必要的特征数量。
主成分分析还可以用于数据预处理,减少数据噪声和冗余,从而提高后续分析的效果。
相比之下,因子分析(Factor Analysis)是一种非线性降维技术,它假设原始数据中的观测值是由一组潜在因子造成的,并且通过这些潜在因子来解释观测值的协方差结构。
因子分析的目标是找到最小的因子数量,能够最好地解释观测值的变异性。
因子分析的步骤如下:1.对原始数据进行标准化。
2.构建因子模型,包括确定因子数量和定义因子之间的关系。
3.通过最大似然估计或最小二乘法等方法,估计因子载荷矩阵,描述观测变量和潜在因子之间的线性关系。
4.通过因子旋转,调整因子载荷矩阵的结构,使得因子之间更容易解释,并且使得观测变量和因子之间的关系更简洁。
5.根据因子载荷矩阵,计算每个因子的得分,得到降维后的数据集。
因子分析在社会科学研究和心理学研究中得到了广泛的应用。
它可以用于构建潜在变量模型,检验假设和推断因果关系。
因子分析可以帮助我们理解观测数据中的潜在结构,提取出隐藏的特征,发现变量之间的关系,并用较少的因子代表观测变量。
主成分分析和因子分析之间存在一些差异。
首先,主成分分析是一种无监督学习方法,不需要预先定义因子的数量和含义,而因子分析需要根据实际问题确定因子的数量和解释,需要一定的先验知识。
其次,主成分分析假设原始数据的变量之间是线性相关的,而因子分析假设原始数据是由潜在因子引起的,可以属于非线性关系。