7正交试验设计

例如，要考察增稠剂用量、pH值和杀菌温度对豆奶稳
定性的影响。每个因素设置3个水平进行试验 。 A因素是增稠剂用量，设A1、A2、A3 3个水平；B因 素是pH值，设B1、B2、B3 3个水平；C因素为杀菌温度， 设C1、C2、C3 3个水平。这是一个3因素3水平的试验，各
因素的水平之间全部可能组合有27种 。
1.3.2 正交表的基本性质
1.3.2.1 正交性 （1）任一列中，各水平都出现，且出现的次数相等 例如L8(27)中不同数字只有1和2，它们各出现4次； L9(34)中不同数字有1、2和3，它们各出现3次 。
上一张 下一张 主 页
退 出
（2）任两列之间各种不同水平的所有可能组 合都出现，且出现的次数相等
（2） 选因素、定水平，列因素水平表
根据专业知识、以往的研究结论和经验，从影响试验指标的
诸多因素中，通过因果分析筛选出需要考察的试验因素。一般确
定试验因素时，应以对试验指标影响大的因素、尚未考察过的因
素、尚未完全掌握其规律的因素为先。试验因素选定后，根据所
掌握的信息资料和相关知识，确定每个因素的水平，一般以2-4
素自由度+交互作用自由度+误差自由度。
此例有4个3水平因素，可以选用L9(34)或
L27(313) ；因本试验仅考察四个因素对液化率的影
响效果，不考察因素间的交互作用，故宜选用 L 9
（ 3 4 ）正交表。若要考察交互作用，则应选用
4-3 因素水平表
试验因素
水平
加水量 （mL/100g） A
10 50 90
加酶量 （mL/100g） B
1 4 7
酶解温度 （℃） C
20 35 50
酶解时间 （h） D

表头设计是借助于与正交表匹配的两 列间交互作用表来完成的。 列间交互作用表来完成的。 例如，要安排A 例如，要安排A、B、C三个因素，每 三个因素， 个因素都是两个水平， 个因素都是两个水平，同时要研究交 互作用A 可选用L 互作用A×B和A×C，可选用L8(27)。查 交互作用表（见表7 L8(27) 交互作用表（见表7-5）。
表头设计：
表头是指正交表第一行的“列号” 表头是指正交表第一行的“列号”。正交表选 定后， 定后，要把各因素项及交互作用项分别放在正交 表表头适当的列中去。此过程称表头设计。 表表头适当的列中去。此过程称表头设计。若因 素间的交互作用可以忽略时， 素间的交互作用可以忽略时，可随意地把各因素 安排在所选表的列上；若因素间有交互作用， 安排在所选表的列上；若因素间有交互作用，则 应将交互作用看作是影响因素， 应将交互作用看作是影响因素，并将其安排在相 应的列上（称为交互作用列）。但是， ）。但是 应的列上（称为交互作用列）。但是，各个因素 列和交互作用列是不能随意安排的。 列和交互作用列是不能随意安排的。表头设计不 是唯一的，一项试验， 是唯一的，一项试验，可以做出多种不同的表头 设计，一般来说，只要设计得合理， 设计，一般来说，只要设计得合理，试验误差不 结论一般都是一致的。 大，结论一般都是一致的。
（2）综合平衡法 先对每个指标分别进行单指标的直 观分析， 观分析，得到每个指标的影响因素主 次顺序和较优水平组合， 次顺序和较优水平组合，然后根据理 论知识和实践经验， 论知识和实践经验，对各指标的分析 结果进行综合比较和分析， 结果进行综合比较和分析，得出较优 方案。 方案。 例7-7
3.2 方差分析法
3.1.2 混合水平试验 常用的方法有两种： 常用的方法有两种： （1）直接利用混合水平的正交表 例7-4

例7-1：用石墨炉原子吸收分光光度计测定食品中 的铅，为提高测定灵敏度，希望吸光度(y)大。为 提高吸光度，讨论了x1(灰化温度/℃)， x2(原子化 温度/℃)和 x3 (灯电流/mA)三个因素对吸光度的影 响，并考虑交互作用x1x2 ， x1x3 。已知x1＝ 300~700℃， x2＝1800~2400℃，x3＝8~10mA。 试通过回归正交试验确定吸光度与三个因素之间
指标（y）与m个试验因素x1，x2，…，xm之间的一次回归
方程：
m
yˆ a bj x j
bkjxk x j , k 1,2,..., m 1( j k)
j 1
k j
例：m＝3时，一次回归方程： y＝a＋b1x1＋b2x2＋b3x3＋b12x1x2＋b13x1x3＋b23x2x3
➢ 其中x1，x2，x3表示3个因素；x1x2，x1x3，x2x3表示交互作用 ➢ 若不考虑交互作用，为三元一次线形回归方程：
➢ 根据偏回归系数的正负，得到各因素对试验指标 的影响方向
(4)方差分析
SST
n i 1
yi2
1( n n i1
yi )2
2.049044
4.0382 8
0.010864
SS1 mcb12 8 0.009752 0.000761
SS2 mcb22 8 0.033752 0.009113
0.010741
SSe SST SSR 0.010864 0.010741 0.000123
(4)方差分析
dfT=n-1=8-1=7 df1=df2=df3=1 df12=df13=1 dfR=df1+df2+df3+df12+df13=1+1+1+1+1=5 dfe=dfT-dfR=7-5=2 MS1=SS1/df1=0.000761 MS2=SS2/df2=0.009113 MS3=SS3/df3=0.000265 MS12=SS12/df12=0.000181 MS13=SS13/df13=0.000421 MSR=SSR/dfR=0.010741/5=0.002148 MSe=SSe/dfe=0.000123/2=0.000062 F1=MS1/MSe=0.000761/0.000062=12.27 F2=MS2/MSe=0.009113/0.000062=146.98 F3=MS3/MSe=0.000265/0.000062=4.27 F12=MS12/MSe=0.000181/0.000062=2.92 F13=MS13/MSe=0.000421/0.000062=6.79 FR=MSR/MSe=0.002148/0.000062=34.65

第7章-正交试验设计的极差分析第7章正交试验设计的极差分析正交试验设计和分析⽅法⼤致分为⼆种：⼀种是极差分析法(⼜称直观分析法),另⼀种是⽅差分析法（⼜称统计分析法)。

本章介绍极差分析法,它简单易懂,实⽤性强，在⼯农业⽣产中⼴泛应⽤。

７.1 单指标正交试验设计及其极差分析极差分析法简称R 法。

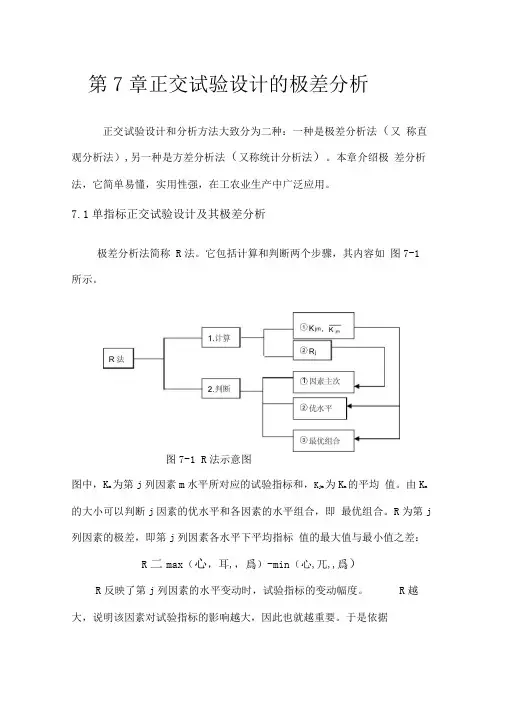
它包括计算和判断两个步骤,其内容如图7-1所⽰。

图7－１ R 法⽰意图图中，Ｋj ｍ为第ｊ列因素m ⽔平所对应的试验指标和，K ｊm 为Ｋjm 的平均值。

由K jm 的⼤⼩可以判断ｊ因素的优⽔平和各因素的⽔平组合，即最优组合。

R j 为第j 列因素的极差，即第j 列因素各⽔平下平均指标值的最⼤值与最⼩值之差：R j =max(jm j j K K K ,,,21 ）-ｍin(jm j j K K K ,,,21 )R j 反映了第ｊ列因素的⽔平变动时，试验指标的变动幅度。

R j 越⼤,说明该因素对试验指标的影响越⼤，因此也就越重要。

于是依据R j的⼤⼩,就可以判断因素的主次。

极差分析法的计算与判断,可直接在试验结果分析表上进⾏，现以例6-2来说明单指标正交试验结果的极差分析⽅法。

⼀、确定因素的优⽔平和最优⽔平组合例６-2 为提⾼⼭楂原料的利⽤率，某研究组研究了酶法液化⼯艺制造⼭楂精汁。

拟通过正交试验寻找酶法液化⼯艺的最佳⼯艺条件。

在例6-2中，不考虑因素间的交互作⽤(因例6-2是四因素三⽔平试验，故选⽤L9（34）正交表），表头设计如表６-５所⽰,试验⽅案则⽰于表６-6中。

试验结果的极差分析过程，如表7-1所⽰.表6-4 因素⽔平表表6-6 试验⽅案及结果试验指标为液化率，⽤y i 表⽰，列于表6-６和表7-1的最后⼀列。

表7－1 试验⽅案及结果分析计算⽰例：因素A 的第１⽔平Ａ1所对应的试验指标之和及其平均值分别为：K A １=ｙ１+y ２+ｙ3＝0+１７+２4=４1,=1A K 31K A1=１3．7同理，对因素Ａ的第2⽔平Ａ２和第３⽔平A 3，有ＫA2=ｙ4+ｙ5+y 6=１２＋47＋28=87,=2A K 31K Ａ2=2９ K A ３＝y ７+y 8＋y ９=１＋18+42＝61，=3A K 31K Ａ3=20.３由表7－１或表6－６可以看出，考察因素A 进⾏的三组试验中(Ａ1,A 2,Ａ3),B 、Ｃ、D 各⽔平都只出现了⼀次,且由于B 、C 、Ｄ间⽆交互作⽤,所以B 、C 、D 因素的各⽔平的不同组合对试验指标⽆影响，因此，对A 1、Ａ2和A ３来说,三组试验的试验条件是完全⼀样的。

正交试验设计方法讲义及举例正交试验设计方法是一种多因素试验设计方法，它能够有效地减少试验所需的样本数量，提高试验结果的精确性和可靠性。

正交试验设计方法是在已知因素水平的情况下选择对试验结果影响最大的因素进行研究的一种方法。

以下是正交试验设计方法的讲义及举例：一、正交试验设计方法的原理及步骤：1.原理：正交试验设计方法通过选择适当的正交表，将多个因素的不同水平组合进行排列，使各因素的变化对试验结果影响均匀化，从而获得准确可靠的试验结果。

2.步骤：a.确定试验因素及其水平：根据试验目的确定需要研究的因素及其水平。

b.选择正交表：根据试验因素的个数和水平确定适用的正交表，正交表能够保证试验结果的均匀性和可靠性。

c.设计试验方案：根据选择的正交表，将试验因素的水平进行组合，获得试验方案。

d.进行试验：按照试验方案进行实际试验。

e.分析试验结果：对试验结果进行统计分析，获得对试验因素的影响程度及其交互作用等信息。

f.微调试验方案：根据试验结果微调试验方案，迭代优化试验过程。

二、正交试验设计方法的优点：1.降低样本数量：正交试验设计方法能够通过对试验水平的排列组合，使试验因素的水平均匀分布，从而减少试验所需的样本数量。

2.提高试验效率：正交试验设计方法能够在有限样本量下获得更多的试验信息，提高试验效率。

3.确保结果可靠：正交试验设计方法通过保证试验因素的均匀分布，减少人为因素的干扰，从而保证试验结果的可靠性和准确性。

4.揭示因素交互作用：正交试验设计方法能够揭示因素之间的交互作用，进一步优化设计过程。

三、正交试验设计方法的举例：例如，公司要研究一种新的洗发水对头发柔顺度的影响，试验主要包括3个因素：洗发水品牌(A、B、C)、洗发水用量(X、Y、Z)和洗发水停留时间(T1、T2、T3)。

根据正交试验设计方法，按照以下步骤进行设计：1.选择正交表：根据3个因素和各因素的水平，选择适用的正交表，如L9正交表。

2.设计试验方案：根据L9正交表，将3个因素的水平进行组合，得到9个试验方案，每个方案分别测试一种组合情况。

五、进行试验
试验结果记录并填入正交表的最后一列。
第三节 正交试验结果分析
一、因素之间没有交互作用的正交试验。
例：某厂某车间对影响产品的质量原因进行研究。
1、试验指标：产品不合格率y，越小越好。
2、确定因素水平：影响产品质量的因素经分 析当时的主要因素有3个：①操作方式，该车间 采用三种操作方式（水平3）。②班组成员的技 术水平，当时有3个等级（水平3）。③产品的 种类，该车间生产用原料有3类（水平3）。
第二节 正交试验计划的安排
一、明确试验目的，确定试验的考核目标。
﹝如某药厂某药品收得率不理想，经常出现 收得率偏小的质量问题。因此改进工艺操 作规程，探求较好的工艺条件，这就是试 验的目的，考核指标就是药品的收得率。 ﹞
二、挑因素，选水平，制定因素水平表。
﹝挑因素，选水平应充分发挥有关人员的理 论知识、专业技术和生产经验等特长，把 因素与水平找得比较准确。﹞
351
361 359 359
356 372
373
363 365 365
12
20
22
2
6
6
1、直观分析
在8个试验中，收得率最高为第6号试验。 其 使试收验得条率件更为高A呢2B？1C这2D需1。要有计没算有一更下好。的条件
2、计算分析
对正交的试验结果，通过简单的计算，往
往能找到更好的条件。分别计算出各因素的 各个水平结果之和﹝I II﹞及各因素的各个水 平结果和之差 。因素的主次排列顺序是：
列号
1
2
3
试验号
1
1
1
1
2
2
1
2
3
1
2
2
4

正交表常用拉丁字母（如L、N等）表示，字母的下方标有数字，表示该行的次数， 例如L4（2^3）表示一个四水平、三次方的正交表。
正交试验设计的核心思想
通过对试验条件的合理安排，减少试验次数，提 高试验效率，同时保证结果的准确性和可靠性。
通过正交试验设计，可以分析各因素对试验结果 的影响程度，找出最优的试验条件或最优组合。
均衡性
正交试验设计能够保证试验点在试验空间中均匀分布，使得试验结果 具有更好的均衡性和代表性。
简单易行
正交试验设计方法简单易行，易于理解和操作，不需要复杂的数学工 具和编程技能。
统计分析方便
正交试验设计的结果可以通过正交表进行统计分析，计算简单，结果 直观。
缺点
适用范围有限
正交试验设计适用于因子数量 和水平数量不太多的情况，对 于高维度的复杂问题可能不太 适用。
试验设计
采用正交表进行试验设计，确保每个 试验方案具有均衡的代表性。
结果分析
通过方差分析、极差分析等方法，找 出最优的混合肥料配方。
实例二：机械零件的加工工艺优化
目的因素与水平源自通过正交试验设计，优化机械零件的加工 工艺，提高生产效率。
选择切削速度、进给量、切削深度三个工 艺参数作为试验因素，每个因素选取四个 水平。
在农业领域，正交试验设计用于研究 不同种植条件和施肥方案对农作物产 量的影响。
化学工业
在化学工业中，正交试验设计用于确 定最佳的化学反应条件，提高生产效 率和产品质量。
02
正交试验设计的基本原理
正交表的概念
正交表是一套规则，用于安排多因素多水平的试验，其特点是每个因素在试验中 出现的次数相等，且在各次试验中因素的排列顺序相同。
正交试验设计方法

它利用正交表来安排试验，确保每个 因素在每个水平上都有机会出现，并 且各因素各水平之间具有均衡分布的 特点。
正交试验设计的特点
高效性
通过合理地选择因素和水平，正交试验设计能够用较少的试验次数获 得较为全面的试验结果，提高试验效率。
均衡性
正交试验设计能够保证每个因素在每个水平上都有机会出现，且各因 素各水平之间具有均衡分布的特点，避免了试验结果的偏差。
试验设计与数据分析(正交试 验设计)
目录
• 试验设计基础 • 正交试验设计 • 正交试验设计的应用 • 正交试验设计案例分析 • 正交试验设计的优缺点 • 正交试验设计的未来发展
01
试验设计基础
试验设计的基本概念
试验设计
指在研究过程中，根据研究目的， 选择适当的试验因素，并按照一 定的原则和方法，安排试验过程， 以得到可靠的科学结论。
试验设计的原则
01
随机性原则
确保试验结果的随机性和代表性。
科学性原则
根据研究目的和研究对象的性质选 择适当的试验方法和手段。
03
02
重复性原则
保证试验结果的可信度和精确度。
经济性原则
在满足研究目的的前提下，尽可能 地节约人力、物力和财力。
04
02
正交试验设计
正交试验设计的定义
正交试验设计是一种通过正交表来安 排多因素多水平试验的方法，旨在通 过合理地选择试验因素和水平，以最 少的试验次数获得尽可能多的信息。
定制化
针对不同领域和特定需求，正交试验设计将更加注重定制化服务，提供个性化的试验方 案和数据分析方法。
未来展望
01
拓展应用领域
随着正交试验设计的不断完善和发展 ，其应用领域将进一步拓展，不仅局 限于工业和工程领域，还将渗透到生 物、医学、社会科学等多个领域。

R j max Tij min Tij
i
R j max Tij min Tij
i

i

i
极差越大，说明这个因素的水平改变对试验结果的 影响越大，极差最大的那个因素，就是最主要的因素。 对例1来说，各因素的主次顺序为
A B A C C D A B
注意：主效应因素尽量不放交互列。如A、B因 素已放C1、C2列，则C 因素就不放C3列。
考虑交互作用AB和AC，则例1的表头可设计为 花菜留种的表头设计
列号 因子 1 2 3 4 5 6 7
A
B
A B
C
A C
D
按正交表 L8 27 得试验方案：

只需将各列中的数字“1”、“2”分别理解为所填因素 在试验中的水平数，每一行就是一个试验方案。
7
7

表示
L8 2
表示各因素的水平数为2，
做8次试验，最多考虑7个
因素（含交互作用）的正
交表。
正交表的特点
表示：在试验安排中，所挑选出来的水平组合是均匀 分布的（每个因素的各水平出现的次数相同） ——均衡分散性 2、正交表中任意两列，把同行的两个数字看成有序数 对时，所有可能的数对出现的次数相同。 表示：任意两因素的各种水平的搭配在所选试验中出现 的次数相等 ——整齐可比性
注：第6列为空白列，当随机误差列；也可把第7列 作空白列。一般要求至少有一个空白列。
第三步 按所选定的正交试验方案组织试验，记录试验 结果；
水 列 平 号 试验号
1 2 3 4 5 6 7 8
A 1 1 1 1 1 2 2 2 2
B 2 1 1 2 2 1 1 2 2

医学研究
用于探索最佳的药物剂量、治疗方案等。
农业科学研究
用于研究不同肥料、农药、种植方式等对农 作物产量的影响。
化学工业
用于研究不同反应条件对化学反应的影响， 提高产物的收率和质量。
正交试验设计的原则
1 2
均衡分布原则
确保每个因素每个水平的试验条件都有机会出现， 避免结果的片面性。
整齐可比原则
保证试验结果的可比性，以便进行数理统计分析。
案例二：化学反应中的正交试验设计
在化学反应中，正交试验设计用于研究不同反应条件 对产物收率和纯度的影响。
例如，在合成某种药物中间体的过程中，通过正交试 验设计来探究温度、压力、催化剂种类和浓度对产物
收率和纯度的影响。
通过优化反应条件，可以提高产物的收率和纯度，降 低生产成本并提高生产效率。
案例三：生物医学研究中的正交试验设计
安排试验计划
总结词：计划性
详细描述：根据正交表，安排详细的 试验计划。这一步骤包括确定试验的 各个水平、组合方式以及试验的顺序 等。合理的试验计划有助于提高试验 的效率和准确性。
实验结果分析
总结词：分析性
VS
详细描述：在完成试验后，对试验结 果进行统计分析。这一步骤包括数据 的整理、处理、分析和解释等。通过 结果分析，可以得出关于试验因素对 试验结果影响的结论，并据此优化试 验方案或进行进一步的研究。
正交试验设计案例分
05
析
案例一：材料科学中的正交试验设计
材料科学中，正交试验设计常用于研究不同材 料成分和工艺参数对材料性能的影响。
例如，在钢铁冶炼过程中，通过正交试验设计 来探究不同温度、压力、时间和合金元素对钢 材强度、韧性和耐腐蚀性的影响。
通过对试验结果的分析，可以确定最佳的工艺 参数组合，从而提高产品质量和降低生产成本。

第7章正交试验设计的极差分析正交试验设计和分析方法大致分为二种：一种是极差分析法（又称直观分析法）,另一种是方差分析法（又称统计分析法）。

本章介绍极差分析法，它简单易懂，实用性强，在工农业生产中广泛应用。

7.1单指标正交试验设计及其极差分析极差分析法简称R法。

它包括计算和判断两个步骤，其内容如图7-1所示。

图7-1 R法示意图图中，K m为第j列因素m水平所对应的试验指标和，K jm为K m的平均值。

由K m 的大小可以判断j因素的优水平和各因素的水平组合，即最优组合。

R为第j 列因素的极差，即第j列因素各水平下平均指标值的最大值与最小值之差：R二max（心，耳,，爲）-min（心,兀,,爲）R反映了第j列因素的水平变动时，试验指标的变动幅度。

R越大，说明该因素对试验指标的影响越大，因此也就越重要。

于是依据R j的大小，就可以判断因素的主次。

极差分析法的计算与判断，可直接在试验结果分析表上进行，现以例6 - 2来说明单指标正交试验结果的极差分析方法。

一、确定因素的优水平和最优水平组合例6-2为提高山楂原料的利用率，某研究组研究了酶法液化工艺制造山楂精汁。

拟通过正交试验寻找酶法液化工艺的最佳工艺条件。

在例6 -2中，不考虑因素间的交互作用（因例6 - 2是四因素三水平试验，故选用L9（34）正交表），表头设计如表6 - 5所示，试验方案则示于表6 - 6中。

试验结果的极差分析过程，如表7 - 1所示.表6-4 因素水平表表6-6 试验方案及结果试验指标为液化率，用y表示，列于表6 - 6和表7 - 1的最后一一表7-1试验方案及结果分析计算示例：因素A的第1水平A i所对应的试验指标之和及其平均值分别为:1K\i=y i+y2+y3=0+17+24=41, K AI = — K Ai=13.73同理，对因素A的第2水平A和第3水平A,有1K A2=y4+y5+y6=12+47+28=87 K A2=-K A2=2931K A3=y7+y8+y9=1 + 18+42=61 , K A3K A3=20.33由表7 - 1或表6 - 6可以看出，考察因素A进行的三组试验中(A,A2,A3), B、C D各水平都只出现了一次，且由于B C、D间无交互作用，所以B、C D因素的各水平的不同组合对试验指标无影响，因此，对A、A和A来说，三组试验的试验条件是完全一样的。

正交试验设计方法详细步骤正交试验设计方法（Orthogonal experimental design）是一种常用的实验设计方法。

它通过对各因素进行全面的、系统的、经济的检测和试验，确定各因素对结果的影响程度，并找出最优的因素组合，以达到降低产品变异性、提高产品质量和生产效率的目的。

本文将详细介绍正交试验设计方法的步骤。

一、确定试验因素和水平在进行正交试验设计之前，首先需要确定试验因素及其各水平。

试验因素是影响实验结果的各个变量，例如温度、压力、时间等。

每个试验因素可以有多个水平，比如低水平和高水平。

在确定试验因素和水平时，需要考虑实际情况和试验的目的。

二、确定正交表确定试验因素和水平后，需要选择合适的正交表来设计试验。

正交表是用于安排试验的一种工具，可以保证各个试验因素在设计中被充分考虑。

常用的正交表有L9、L12、L16等。

选择正交表时需要考虑试验因素的数量和水平个数，以及实验所能容忍的误差。

三、设计试验方案设计试验方案时，需要根据所选正交表,将试验因素和水平组合起来，形成实验方案。

确保每个水平都得到了充分的考虑和试验。

在设计试验方案时，需注意避免水平间的过大差异，以防止试验结果受到干预。

四、进行实验根据设计好的试验方案，开始进行实验。

在实验过程中，需要准确记录每个因素水平对应的结果数据，以便后续分析和处理。

五、数据分析和处理实验数据收集完毕后，需要对数据进行分析和处理。

常用的数据分析方法包括方差分析、回归分析等。

通过数据分析，可以得到各个因素对结果的影响程度，找出主要影响因素，并确定最优的因素组合。

六、优化因素组合根据数据分析结果，可以进一步优化试验因素的组合。

通过确定最优的因素组合，可以提高产品的质量和效率，降低产品的变异性。

七、验证实验结果在优化因素组合之后，需要进行验证实验，以验证优化结果的有效性和可行性。

验证实验的目的是确保所得到的最优组合在不同条件下仍然有效。

八、总结和应用最后，根据实验结果和验证结果，总结正交试验设计的步骤和方法，并将其应用到实际生产和工程中。

4因素7水平正交试验设计1. 简介4因素7水平正交试验设计是一种统计方法，用于确定多个因素对试验结果的影响。

通过正交设计，我们可以在较少的试验次数下获得全面的数据，从而有效地进行因素分析和优化。

2. 正交设计原理正交设计的核心原理是通过减少试验次数，同时保证各个因素之间的独立性，来获取全面的数据。

正交设计通过选择合适的水平组合，使得各个因素对试验结果的影响都能得到准确的评估。

3. 4因素7水平正交试验设计的步骤3.1 确定试验因素：首先确定需要研究的因素，并确定每个因素的水平数。

3.2 构建正交表格：根据试验因素和水平数，构建正交表格，保证各个因素之间的独立性。

3.3 进行试验数据采集：根据正交表格的设计，进行试验数据的采集。

每个试验对应一组水平组合。

3.4 分析试验结果：通过分析试验结果，评估各个因素对试验结果的影响，并确定最优的水平组合。

4. 应用范围和优势4因素7水平正交试验设计可广泛应用于工程、科学和营销等各个领域。

它的主要优势包括：- 较少的试验次数：相比于传统试验设计，正交设计能够在较少的试验次数下得到全面的数据，节省时间和资源。

- 独立性保证：正交设计能够保证各个因素之间的独立性，准确评估每个因素对试验结果的影响。

- 可解释性强：通过正交设计，我们可以清晰地了解每个因素的作用，从而做出准确的决策和优化。

- 可迭代性强：正交设计可根据试验结果进行迭代，不断优化水平组合，实现更好的试验效果。

5. 总结4因素7水平正交试验设计是一种有效的统计方法，能够在较少的试验次数下获得全面的数据，并评估各个因素对试验结果的影响。

通过正交设计，我们可以做出准确的决策和优化，应用范围广泛，具有较强的可解释性和可迭代性。

正交实验设计当析因设计要求的实验次数太多时，一个非常自然的想法就是从析因设计的水平组合中，选择一部分有代表性水平组合进行试验。

因此就出现了分式析因设计(fractional factorial designs)，但是对于试验设计知识较少的实际工作者来说，选择适当的分式析因设计还是比较困难的。

正交试验设计(Orthogonal experimental design)是研究多因素多水平的又一种设计方法，它是根据正交性从全面试验中挑选出部分有代表性的点进行试验，这些有代表性的点具备了“均匀分散，齐整可比”的特点，正交试验设计是分式析因设计的主要方法。

是一种高效率、快速、经济的实验设计方法。

日本著名的统计学家田口玄一将正交试验选择的水平组合列成表格，称为正交表。

例如作一个三因素三水平的实验，按全面实验要求，须进行33=27种组合的实验，且尚未考虑每一组合的重复数。

若按L9(3)3正交表按排实验，只需作9次，按L18(3)7正交表进行18次实验，显然大大减少了工作量。

因而正交实验设计在很多领域的研究中已经得到广泛应用。

1．正交表正交表是一整套规则的设计表格，用。

L为正交表的代号，n为试验的次数，t为水平数，c为列数，也就是可能安排最多的因素个数。

例如L9(34)，(表11)，它表示需作9次实验，最多可观察4个因素，每个因素均为3水平。

一个正交表中也可以各列的水平数不相等，我们称它为混合型正交表，如L8(4×24) (表12)，此表的5列中，有1列为4水平，4列为2水平。

根据正交表的数据结构看出，正交表是一个n行c列的表，其中第j列由数码1，2，… S j组成，这些数码均各出现N/S次，例如表11中，第二列的数码个数为3，S=3 ，即由1、2、3组成，各数码均出现次。

正交表具有以下两项性质：(1)每一列中，不同的数字出现的次数相等。

例如在两水平正交表中，任何一列都有数码“1”与“2”，且任何一列中它们出现的次数是相等的；如在三水平正交表中，任何一列都有“1”、“2”、“3”，且在任一列的出现数均相等。

正交试验设计的基本程序和步骤1、前言正交试验设计（Orthogonal experimental design，OED）是一种重要的统计学方法，它可以有效地降低试验次数和成本，并且在较短时间内获得较为全面的试验结果。

在实际的工程应用中，正交试验设计被广泛地应用于产品设计、工艺优化、性能分析等方面。

在本文中，将分析正交试验设计的基本程序和步骤，以便读者更好地了解和应用它。

2、正交试验设计的基本概念和目的正交试验设计是一种实验设计方法，它的核心思想是在尽量少的试验次数内，获得尽量全面的试验结果。

正交试验设计的目的是确定试验因素对试验结果的影响关系，以便在最短的时间内找到最优的试验方案。

在正交试验设计中，试验因素是指影响试验结果的因素，它包括五个要素，即A(B)、B(C)、C(A)、D(E)、E(D)，其中ABC是三因素正交设计，DE是两因素正交设计。

试验因素水平是指了试验因素的取值，例如低水平（-1）和高水平（1）。

3、正交试验设计的基本步骤（1）确定试验因素和水平在正交试验设计中，首先需要明确试验的主要因素，以及试验因素的水平。

在实际的试验中，因素的数量和水平的设置应该根据具体试验问题来确定，同时，要注意试验因素个数的控制，以避免试验运行过多。

（2）构建试验方案矩阵试验方案矩阵是正交设计的核心，它是一种特殊的矩阵，将试验因素和水平按照一定的规则排列组合。

在构建试验方案矩阵时，需要考虑多个因素对试验结果的影响，以避免试验设计的偏差。

（3）实施试验方案并收集数据在实际的试验中，需要根据试验方案进行试验并收集数据。

在试验过程中要注意严格的试验控制和数据收集，以避免实验结果的不准确性。

（4）数据分析数据分析是正交试验设计的关键步骤，通过数据分析可以确定试验因素的影响关系，并找到最优的试验方案。

数据分析的过程一般包括方差分析、回归分析等统计学方法。

（5）确定优化方案根据数据分析结果，确定试验因素的优化方案，找到最优的试验方案。

正交试验设计及分析(多实现途径)引言概述:正交试验设计是一种重要的统计方法，用于确定实验中不同因素对结果的影响。

它可以帮助研究者系统地设计实验，降低实验数量和成本，并提供可靠的分析结果。

本文将介绍正交试验设计的概念、原理，以及多种实现途径，以便读者根据自身需求选择合适的方法进行实验。

正文内容:1.正交试验设计的概念和原理:1.1定义:正交试验设计是一种通过系统地变动因素水平来确定因素对结果的影响的方法。

它将多个因素分解为一些离散的水平，以便在有限实验中进行测试。

1.2原理:正交试验设计基于正交矩阵的原理，该矩阵具有特定的数学性质，可以保证不同因素之间的相互独立性，从而减少实验数量。

2.正交试验设计的多实现途径:2.1Taguchi方法:Taguchi方法是一种常用的正交试验设计方法，它通过选择最优的因素水平组合来优化结果的表现。

它能够在较少的实验次数下找到最佳的因素配置。

2.2BoxBehnken设计:BoxBehnken设计是一种常用的三水平正交试验设计方法，适用于3个或更多个因素的试验。

它通过正交矩阵将因素水平组合成三水平，并通过优化方法确定最佳结果。

2.3中心组合设计:中心组合设计是一种将中心点设置为固定因素水平的正交试验设计方法。

该设计方法可以估计因素对结果的线性和二次的影响，适用于连续和离散因素。

2.4贝叶斯优化设计:贝叶斯优化设计是一种基于贝叶斯统计模型的正交试验设计方法。

它能够在先验知识不完全或验证数据有限的情况下，利用概率推论来确定最佳因素配置。

3.正交试验设计的分析方法:3.1方差分析:方差分析是一种常用的正交试验设计分析方法，用于确定各个因素之间的显著性差异。

它通过计算方差的比值来判断因素对结果的影响程度。

3.2回归分析:回归分析是一种统计方法，用于描述和预测因变量与一个或多个自变量之间的关系。

在正交试验设计中，回归分析可以用来确定因素对结果的线性和非线性影响。

3.3主效应图:主效应图是一种简明直观的分析方法，通过图形展示各个因素对结果的平均水平差异。

第7章-正交试验设计的极差分析汇总第7章正交试验设计的极差分析正交试验设计和分析方法大致分为二种：一种是极差分析法（又称直观分析法）,另一种是方差分析法（又称统计分析法）。

本章介绍极差分析法，它简单易懂，实用性强，在工农业生产中广泛应用。

7.1单指标正交试验设计及其极差分析极差分析法简称R法。

它包括计算和判断两个步骤，其内容如图7-1所示。

图中，K m为第j列因素m水平所对应的试验指标和，K jm为K m的平均值。

由K m的大小可以判断j因素的优水平和各因素的水平组合，即最优组合。

R为第j列因素的极差，即第j列因素各水平下平均指标值的最大值与最小值之差：R j=max（K~i,K~2, ,K jm）-min（心,兀，,K~）R反映了第j列因素的水平变动时，试验指标的变动幅度。

R 越大，说明该因素对试验指标的影响越大，因此也就越重要。

于是依据R j的大小，就可以判断因素的主次极差分析法的计算与判断，可直接在试验结果分析表上进行，现以例6 - 2来说明单指标正交试验结果的极差分析方法。

一、确定因素的优水平和最优水平组合例6-2为提高山楂原料的利用率，某研究组研究了酶法液化工艺制造山楂精汁。

拟通过正交试验寻找酶法液化工艺的最佳工艺条件。

在例6 -2中，不考虑因素间的交互作用（因例6 - 2是四因素三水平试验，故选用L9（34）正交表），表头设计如表6 - 5所示，试验方案则示于表6 - 6中。

试验结果的极差分析过程，如表7 - 1所示.表6-4 因素水平表表6-6 试验方案及结果试验指标为液化率，用y i表示，列于表6 - 6和表7 - 1的最后一一计算示例:因素A的第1水平A i所对应的试验指标之和及其平均值分别为:K AI二y i+y2+y3=0+17+24=41, K A1同理，对因素A的第2水平A和第3水平A,有-K AI=13.7 31K A2=y4+y5+y6=12+47+28=87 K A2 K A2=2931K A3=y7+y8+y9=1 + 18+42=61 , K A3K A3=20.33由表7 - 1或表6 - 6可以看出，考察因素A进行的三组试验中(A,A2,A3)，B、C D各水平都只出现了一次，且由于B、C D间无交互作用，所以B、C D因素的各水平的不同组合对试验指标无影响，因此，对A、A2和A s来说，三组试验的试验条件是完全一样的。