下载文档原格式
算法循环结构教学目标：知识与技能：1.熟悉循环结构，理解当型结构和直到型结构。
2.熟悉两种循环结构的各自特点与区别。
3.能将具体问题用两种循环结构程序框图表达。
过程与方法：通过模仿、操作、探究，学习设计循环结构程序框图，体会算法思想，发展有条理的思考与表达能力，提高逻辑思维。
情感、态度、价值观：感受和体会到算法思想在解决具体问题中的意义，增强我们的创新能力及应用数学的意识。
教学重点：理解当型结构和直到型结构。
教学难点：循环结构中判断条件的选择，当型结构和直到型结构的区别。
教学过程：一、 导入新课1.算法的基本逻辑结构有哪几种？用程序框图如何表示？ 顺序结构，由若干个依次执行的步骤组成的。
条件结构，算法的流程根据条件是否成立有不同的流向，根据不同的流向执行不同的步骤。
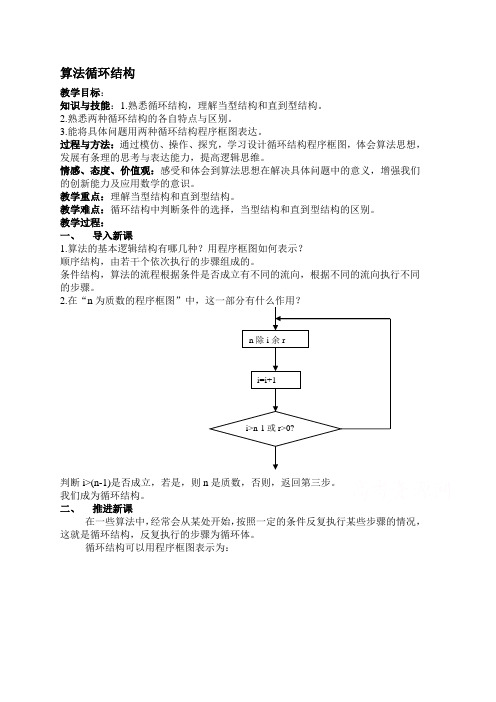
2.在“n判断i>(n-1)是否成立，若是，则n 是质数，否则，返回第三步。
我们成为循环结构。
二、 推进新课在一些算法中，经常会从某处开始，按照一定的条件反复执行某些步骤的情况，这就是循环结构，反复执行的步骤为循环体。
循环结构可以用程序框图表示为：这个循环结构有如下特征：在执行了一次循环体后，对条件进行判断，如果条件不满足，就继续执行循环体，直到条件满足时终止循环.因此，这种循环结构称为直到型循环结构.除直到型循环结构外，还有当型循环结构，它有如下特征：在每次执行循环体前，对条件进行判断，当条件满足时，执行循环体，否则终止循环.它可以用程序框图示为：循环结构一定包含条件结构，用于确定何时终止执行循环体。
三、例题讲解例1 设计一个计算1+2+3+…+100的值的程序框图。
算法分析：通常我们按下列过程计算1+2+3+…+100的值。
第1步： 0+1=1第2步： 1+2=3第3步： 3+3=6第4步： 6+4=10……第100步：4950+100=5050显然，这个过程中包含重复操作的步骤，可以用循环结构表示。
第i-1步的结果+i=第i步的结果s=s+i i=1.2.3 (100)解决这一问题的算法是：第一步：令i=1,s=0。
算法的3种基本结构算法是指一系列有限指令的集合，它通过一定的顺序和逻辑关系来解决问题。
简单来说，算法就是一种解决问题的方法。
通常，算法可以分为三种基本结构：顺序结构、选择结构和循环结构。
下面将详细介绍这三种结构及其在算法中的应用。
1.顺序结构：顺序结构是指按照所给指令的先后顺序依次执行，一般没有条件判断和循环语句。
在顺序结构中，每个指令将依次执行，并且每个指令只执行一次。
这种结构常用于一些简单直接的操作，如输入输出、变量赋值等。
顺序结构的一个典型例子是求解两个数相加的过程。
2.选择结构：选择结构是指根据条件的不同选择不同的操作路径。
它通常使用条件判断语句，如if-else语句、switch语句等。
根据条件的真假，程序可以选择执行其中一部分代码，或者跳过其中一部分代码。
选择结构可以根据特定的条件来选择不同的执行路径，从而实现不同的功能。
这种结构常用于进行判断和决策的场景，如根据用户输入的选择进行不同的操作。
3.循环结构：循环结构是指重复执行其中一段操作，直到满足一些条件停止。
它通常使用循环语句，如while循环、for循环等。
循环结构可以重复执行一段代码多次，从而实现对数据的多次处理和操作。
循环结构的一个典型应用是遍历数组或链表，对其中的每个元素进行相同的操作。
循环结构可以大大减少代码的冗余，提高代码的复用性和可维护性。
这三种基本结构是算法设计中最基础、最常见的结构，它们在实际应用中经常与其他结构组合使用。
算法的实际应用中，往往需要根据问题的不同选择合适的结构来解决。
例如，对于一些复杂的问题，可能需要同时使用选择结构和循环结构来解决。
此外，通过合理使用这三种基本结构，可以提高算法的效率和可读性，从而更好地解决问题。
总结起来，算法的三种基本结构，顺序结构、选择结构和循环结构，分别表示了按顺序执行、根据条件选择和重复执行的不同操作方式。
通过合理运用这些结构，可以编写出高效、简洁、可读性强的算法，从而更好地解决各种实际问题。
