fortran常用算法的程序设计举例

fortran常用算法程序集Fortran是一种广泛用于科学和工程计算的编程语言。

由于其强大的数值计算能力，Fortran在许多领域，如物理、数学、工程和生物信息学中，仍然被广泛使用。

在Fortran中，有许多常用的算法可以用来解决各种计算问题。

下面是一些常用的Fortran算法程序集的示例。

1.冒泡排序算法```fortranPROGRAMBubbleSortIMPLICITNONEINTEGER,DIMENSION(:),ALLOCATABLE::arrINTEGER::i,j,tempALLOCATE(arr(10))!分配数组空间!填充数组数据arr=[9,8,7,6,5,4,3,2,1,0]DOi=1,SIZE(arr)-1DOj=i+1,SIZE(arr)IF(arr(j)>arr(j-1))THEN!交换相邻元素temp=arr(j)arr(j)=arr(j-1)arr(j-1)=tempENDIFENDDOENDDOPRINT*,"排序后的数组："PRINT*,arr(:)ENDPROGRAMBubbleSort```这个程序使用冒泡排序算法对一个整数数组进行排序。

冒泡排序是一种简单的排序算法，通过重复地遍历要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。

这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

2.二分查找算法```fortranPROGRAMBinarySearchIMPLICITNONEINTEGER::arr(10),low,high,found=0INTEGER::mid=0PRINT*,"请输入要查找的元素："INPUT(INTEGER)::xlow=0high=SIZE(arr)-1DOWHILE(found==0)!直到找到元素或数组遍历完为止mid=(low+high)/2!计算中间位置IF(arr(mid)==x)THEN!如果中间元素等于要查找的元素，则找到found=1!设置found标志为1，表示找到元素ELSEIF(arr(mid)>x)THEN!如果中间元素大于要查找的元素，则在左半部分查找high=mid-1!将high指向中间元素的左边的位置ELSE!如果中间元素小于要查找的元素，则在右半部分查找low=mid+1!将low指向中间元素的右边的位置ENDIFENDDOIF(found==0)PRINT*,"元素未找到。

fortran排序函数Fortran是一种编程语言，它在科学计算和数值分析领域广泛应用。

在这篇文章中，我们将讨论如何使用Fortran编写排序函数。

排序是一种常见的操作，它可以对一组数据按照特定的顺序进行排列。

在计算机科学中，有许多不同的排序算法可供选择，例如冒泡排序、插入排序、选择排序、快速排序等。

在Fortran中，我们可以使用这些算法来实现排序函数。

让我们来看看冒泡排序算法在Fortran中的实现。

冒泡排序的基本思想是通过相邻元素之间的比较和交换来逐步将最大（或最小）的元素移动到正确的位置。

下面是一个简单的冒泡排序函数的示例：```subroutine bubble_sort(arr, n)integer, dimension(n) :: arrinteger :: i, j, tempdo i = 1, n-1do j = 1, n-iif (arr(j) > arr(j+1)) thentemp = arr(j)arr(j) = arr(j+1)arr(j+1) = tempend ifend doend doend subroutine```在这个函数中，我们使用了两个循环来遍历数组，并通过比较和交换操作来排序元素。

外部循环`i`控制了需要进行比较的轮数，而内部循环`j`用于比较相邻的元素，并进行交换。

接下来，让我们来看看另一种常见的排序算法——快速排序。

快速排序是一种基于分治思想的排序算法，通过选择一个基准元素，将数组划分为两个子数组，并对子数组进行递归排序来实现整个数组的排序。

下面是一个简单的快速排序函数的示例：```subroutine quick_sort(arr, left, right)integer, dimension(:) :: arrinteger :: left, right, i, j, pivot, tempif (left < right) thenpivot = arr((left+right)/2)i = leftj = rightdo while (i <= j)do while (arr(i) < pivot)i = i + 1end dodo while (arr(j) > pivot)j = j - 1end doif (i <= j) thentemp = arr(i)arr(i) = arr(j)arr(j) = tempi = i + 1j = j - 1end ifend docall quick_sort(arr, left, j) call quick_sort(arr, i, right) end ifend subroutine```在这个函数中，我们首先选择一个基准元素`pivot`，然后使用两个指针`i`和`j`分别从左右两侧开始遍历数组。

Fortran常用算法程序集简介Fortran是一种面向科学和工程计算的编程语言，通常用于数值计算和数据分析。

它有着强大的数学计算能力和高性能，被广泛应用于科学计算、工程仿真、天气预报等领域。

本文将介绍一些常用的Fortran算法程序集，包括数值积分、矩阵运算、排序算法等。

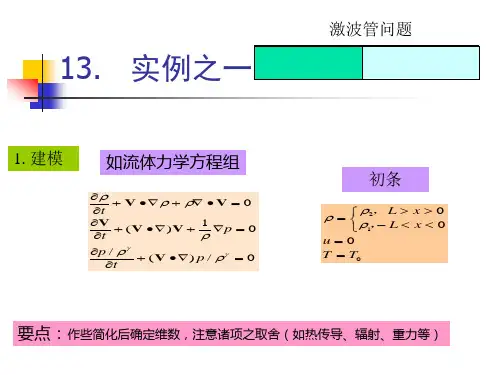
数值积分数值积分是求解定积分的一种方法，用于计算曲线下面积、求解微分方程等。

Fortran提供了一些常用的数值积分算法，如梯形法则、辛普森法则等。

梯形法则梯形法则是数值积分中最简单的算法之一，基本思想是将曲线下面积近似为一系列梯形的和。

下面是使用Fortran编写的梯形法则算法示例：! 梯形法则real function trapezoidal_rule(f, a, b, n)real, external:: freal:: a, b, n, hreal:: x, suminteger:: ih = (b - a) / nsum= f(a) + f(b)do i =1, n-1x = a + i * hsum=sum+2* f(x)end dotrapezoidal_rule = (h/2) *sumend function trapezoidal_rule辛普森法则辛普森法则是一种更精确的数值积分算法，基于多项式插值的思想。

它将曲线分成若干小段，每段近似为一个二次函数，然后对每个二次函数进行积分。

下面是使用Fortran编写的辛普森法则算法示例：! 辛普森法则real function simpsons_rule(f, a, b, n)real, external:: freal:: a, b, n, hreal:: x, sum1, sum2integer:: ih = (b - a) / nsum1 = f(a) + f(b)sum2 =0do i =1, n-1, 2x = a + i * hsum2 = sum2 +4* f(x)end dodo i =2, n-2, 2x = a + i * hsum2 = sum2 +2* f(x)end dosimpsons_rule = (h/3) * (sum1 + sum2)end function simpsons_rule矩阵运算矩阵运算是科学计算中常用的一个重要环节，Fortran提供了丰富的矩阵运算库，包括矩阵乘法、矩阵转置、矩阵求逆等。

对于FORTRA的初学者。

这些例子可作为小练习1.例题：计算工资问题。

每小时工资为RATE如果工作超过40小时，加班呢部分工资是正常时间工资的1.5倍。

C Payroll with overtimeprogram payrollreal rate, hours, payread (*,*) rate, hoursif (hours>40) thenpay=40*rate+(hours-40)*1.5*rateelsepay=hours*rateEND IFprint *, "rate=" , rateprint *, "hours=" , hoursprint *, "pay=" ,payend2•学生成绩问题。

大于80为A级。

大于60小于80为B级。

小于60为C级。

IF的嵌套。

注意空格可以看清楚else if ,e nd if,pri nt 的内容•PROGRAGRADESTUDENTREA0GRADEIF (GRADE .GE. 80) THENPRINT*,GRADE, "GRADE=>A"ELSEIF (GRADELT.60) THENPRINT*,GRADE"GRADE=>C"ELSEPRINT*,GRADE"GRADE=>B"END IFEND IFEND3. 三个数按从小到大排序。

PROGRA M AXMINREALA,B,C,TREA0A,B,CIF (A.GT.B) THENT=AA=BB=TELSEEND IFIF (B.GT.C) THENT=BB=CC=TELSEEND IFIF (A.GT.B) THENT=AA=BB=TEND IFPRINT*,A,B,CEND4. 运用EISE IF语句。

重做例子2PROGRAM2READ*,*) GRADEIF (GRADE .GE. 80.0) THENPRINT*, GRADE, "=>A"ELSE IF(GRADE .GE. 70.0) THENPRINT*, GRADE, "=>B"ELSE IF(GARDE .GE. 60.0) THENPRINT*, GRADE, "=>C"ELSEPRINT*, GARDE, "=>D"END IFEND3x 6,x 05. 计算y 2x 2x 8,x 0PROGRAEQUATIONREAD*,*) XIF (X .GE. 0.0) Y=3*X+6IF (X .LT. 0.0) Y=-X**2+2*X-8PRINT*, "X=" ,X, "Y=" ,YEND6. CONTINUED句。

程序设计基础-Fortran95课程设计课程设计需求本次课程设计的目的是提高学生关于Fortran95程序设计方面的能力和技巧。

为了达到这个目的，课程设计需求如下：1.设计一个可以计算矩形面积和周长的程序。

2.设计一个可以计算圆形面积和周长的程序。

3.设计一个可以将输入的字符串反转的程序。

设计思路矩形面积和周长的程序我们需要设计一个可以计算矩形面积和周长的程序。

矩形的面积公式为：area=lengtℎ∗widtℎ，周长公式为：perimeter=2∗(lengtℎ+widtℎ)。

在Fortran95中，我们可以使用READ语句获取用户输入的length 和width，然后进行计算，最后使用WRITE语句输出结果。

以下是完整代码：PROGRAM rectangleIMPLICIT NONEREAL:: length, width, area, perimeterWRITE(*,*)'Please enter the length of the rectangle:'READ(*,*) lengthWRITE(*,*)'Please enter the width of the rectangle:'READ(*,*) widtharea = length * widthperimeter = 2.0* (length + width)WRITE(*,*)'The area of the rectangle is:', areaWRITE(*,*)'The perimeter of the rectangle is:', perimeter END PROGRAM rectangle圆形面积和周长的程序我们需要设计一个可以计算圆形面积和周长的程序。

圆的面积公式为：$area = \\pi * radius^2$，周长公式为：$circumference = 2* \\pi * radius$。

fortran常用算法程序集
Fortran是一种高级编程语言，用于科学计算和数值分析。

下面是一些常见的Fortran算法程序集：
1. 插值算法：包括线性插值、拉格朗日插值和样条插值。

这些算法用于在给定一组已知数据点的情况下，估计在这些数据点之间的未知数据点的值。

2. 数值积分算法：例如，辛普森规则和龙格-库塔法（Runge-Kutta methods），用于计算函数的定积分。

3. 线性代数算法：例如求解线性方程组（高斯消元法），计算矩阵的特征值和特征向量。

4. 数值优化算法：例如牛顿法和梯度下降法，用于求解非线性优化问题。

5. 快速傅里叶变换（FFT）：用于计算离散傅里叶变换（DFT）的高效算法，常用于信号处理和图像处理。

6. 数值微分和微分方程求解算法：例如欧拉法和龙格-库塔法，用于求解常微分方程。

7. 随机数生成算法：例如梅森旋转算法（Mersenne Twister）和伪随机数生成器。

8. 图论算法：例如最短路径算法（迪杰斯特拉算法和贝尔曼-福特算法）和最小生成树算法（普林斯顿算法）。

这只是一些Fortran中的常见算法，实际上还有许多其他算法可以使用Fortran实现。

这些程序集可在各种Fortran 编程参考资料和库中找到。

fortran常用算法程序集Fortran是一种高级编程语言，广泛应用于科学计算和数值分析领域。

它的强大之处在于它提供了丰富的算法库，使程序开发人员能够快速实现各种常见算法。

本文将介绍一些Fortran常用的算法程序集，帮助读者更好地理解和应用这些算法。

一、线性代数算法线性代数是科学计算和数值分析的基础，Fortran提供了许多用于求解线性方程组、矩阵分解和矩阵运算的算法。

其中一些常用的算法包括：1. 高斯消元法高斯消元法是一种求解线性方程组的方法，可以将线性方程组转化为上三角或下三角矩阵，并进一步求解。

Fortran提供了多种高斯消元法的实现，如LU分解法和托伯利兹矩阵法。

2. 特征值与特征向量计算特征值与特征向量计算是矩阵分解的一种重要问题。

Fortran提供了多种算法来计算矩阵的特征值与特征向量，如幂法、反幂法、QR算法等。

3. 矩阵乘法和矩阵求逆矩阵乘法和矩阵求逆是线性代数中常见的操作。

Fortran提供了多种高效的算法来实现矩阵乘法和矩阵求逆，如Strassen算法、LU分解法等。

二、数值计算算法数值计算算法广泛应用于科学计算、数值模拟和数据分析等领域。

Fortran提供了多种数值计算算法的实现，如数值积分、函数逼近、插值算法等。

以下是一些常用的数值计算算法：1. 数值积分数值积分可以用来对函数进行近似求积，求解曲线下面积或计算定积分。

Fortran提供了多种数值积分方法的实现，如梯形法则、辛普森法则和龙贝格方法等。

2. 函数逼近函数逼近是将多项式或其他数学函数与给定函数进行拟合，用于简化函数计算或数据分析。

Fortran提供了多种函数逼近的方法，如最小二乘逼近、最大误差逼近等。

3. 插值算法插值算法用于根据已知的离散数据点估计未知点的值。

Fortran提供了多种插值算法的实现，如拉格朗日插值法、牛顿插值法和样条插值法等。

三、优化算法优化算法用于求解最优化问题，如寻找函数最大值或最小值的点。

fortran除法Fortran是一种程序设计语言，它在科学计算领域有着广泛的应用。

本文将介绍Fortran除法操作的相关知识，包括除法运算符、数据类型、除数为零的处理以及实际应用案例。

一、Fortran除法运算符Fortran中用于除法运算的运算符是“/”。

它可以用于两个数值变量之间的相除。

例如，若要将变量A除以变量B并将结果存储在变量C中，可以使用以下语句：C = A / B在Fortran中，除法运算符可以应用于整数类型和实数类型的变量。

对于整数类型，除法运算符将执行整数除法，即结果将被截断为整数。

而对于实数类型，除法运算符将执行浮点数除法，即结果保留小数部分。

二、Fortran数据类型在进行除法运算时，需要了解Fortran中的数据类型。

Fortran提供了多种数据类型，包括整数类型（INTEGER）、实数类型（REAL）、双精度实数类型（DOUBLE PRECISION）等。

在进行除法运算时，需要注意操作数的数据类型以及结果的数据类型。

若要进行整数除法，需要使用整数类型的变量作为操作数，并将结果存储在整数类型的变量中。

若要进行浮点数除法，可以使用实数类型或双精度实数类型的变量作为操作数，并将结果存储在相应的实数类型或双精度实数类型的变量中。

以下是一个示例代码，展示了如何定义不同数据类型的变量并进行除法运算：```fortranINTEGER :: a, b, cREAL :: d, e, fa = 10b = 3c = a / bd = 10.0e = 3.0f = d / e```三、处理除数为零的情况在进行除法运算时，需要注意除数为零的情况。

若除数为零，除法操作将会导致错误或异常情况。

为了避免程序异常终止，可以在进行除法运算之前添加判断条件，检查除数是否为零。

若除数为零，可以采取相应的处理措施，例如输出错误信息或进行其他操作。

以下是一个示例代码，展示了如何处理除数为零的情况：```fortranINTEGER :: a, b, ca = 10b = 0IF (b /= 0) THENc = a / bELSEWRITE(*,*) "除数不能为零"END IF```四、实际应用案例Fortran除法在实际应用中有着广泛的应用。

fortran除法（原创版）目录1.Fortran 语言简介2.Fortran 中的除法运算3.Fortran 除法的应用实例4.总结正文1.Fortran 语言简介Fortran（Formula Translation）是一种高级编程语言，主要用于数值计算和科学计算领域。

自 1957 年问世以来，Fortran 语言已经发展成为一个庞大的编程体系，广泛应用于数学、物理、化学、工程等领域的科学计算和数据处理。

2.Fortran 中的除法运算在 Fortran 中，除法运算使用“/”符号表示。

除法运算的结果是一个浮点数。

需要注意的是，Fortran 中的除法运算不支持整数除法，如果需要进行整数除法，需要通过取整函数等方法进行处理。

3.Fortran 除法的应用实例假设有一个简单的计算任务，需要计算一个数组中每个元素的平方根。

可以使用 Fortran 中的除法运算来实现这个功能。

以下是一个简单的示例：```fortranprogram square_rootimplicit noneinteger :: n = 5real :: x(n) = (/ 1, 2, 3, 4, 5 /)real :: y(n)do i = 1, ny(i) = sqrt(x(i))end dodo i = 1, nprint *, "x(", i, ") = ", x(i), " y(", i, ") = ", y(i) end doend program square_root```在上面的示例中，我们定义了一个数组 x，并用 Fortran 中的除法运算为数组 x 的每个元素赋值。

然后，我们通过一个循环计算数组 x 中每个元素的平方根，并将结果存储在数组 y 中。

最后，我们打印出数组 x 和数组 y 的对应元素。

4.总结Fortran 作为一种适用于科学计算的高级编程语言，提供了丰富的数学运算功能，包括除法运算。