【新课标人教A版必修五】高中数学模块过关专题讲座练习：第三讲 正弦定理和余弦定理(习题课)

1.1正弦定理和余弦定理（人教实验A版必修5）建议用时实际用时满分实际得分45分钟100分一、选择题（本大题共7小题，每小题4分，共28分.在每小题给出的四个选项中，只有一项是符合题目要求的）1.在△ABC中，下列各式中符合余弦定理的是（）（1）c2＝a2＋b2－2ab cos C；（2）c2＝a2－b2－2bc cos A；（3）b2＝a2－c2－2bc cos A；（4）cos C＝a2＋b2＋c2－2ab.A.(1)B.(2)C.(3)D.(4)2.在△ABC中，a＝15，b＝10，A＝60°，则cos B=（）A.B.C.D.3.在△ABC中，已知a＝4，b＝6，C＝120°，则边c的长是（）A.B.C.2D.24.已知锐角A是△ABC的一个内角，a,b,c是三角形中各内角的对应边，若sin2A－cos2A＝12，则下列各式正确的是（）（1）b＋c＝2a；（2）b＋c2a；（3）b＋c≤2a；（4）b＋c≥2a.A.(1)B.(2)C.(3)D.(4)5.在△ABC中，D点为BC上一点，BD＝12DC，∠ADB＝120°，AD＝2.若△ADC的面积为3－3，则∠BAC ＝（）A.30°B.60°C.45°D.90°6.如果等腰三角形的周长是底边长的5倍，那么它的顶角的余弦值为（）A.B.C.D.7.在△ABC中，已知2sin A cos B=sin C，那么△ABC的形状是（）三角形.A.锐角B.直角C.等边D.等腰二、填空题（本大题共5小题，每小题5分，共25分.把答案填在题中横线上）8.如图，在四边形ABCD中，已知AD CD，AD=10，AB=14，∠BDA=60︒，∠BCD=135︒，则BC= .9.如图，AA1与BB1相交于点O，AB∥A1B1且AB＝1A1B1.若△AOB的外接2圆的直径为1，则△A1OB1的外接圆的直径为_______．10.在△ABC中，若B＝60°，2b＝a＋c，则△ABC的形状是．(填锐角三角形、直角三角形、钝角三角形)11.在△ABC中，下列关系式：①a sin B＝b sin A；②a＝b cos C＋c cos B；③a2＋b2－c2＝2ab cos C；④b＝c sin A＋a sin C，一定成立的个数是 .12.△ABC的内角A、B、C的对边分别是a、b、c，若B=2A，a=1，b=，则c= .三、解答题（共47分，解答应写出文字说明，证明过程或演算步骤）13.（11分）在△ABC中，b＝a sin C，c＝a cos B，试判断△ABC的形状．14.（12分）在锐角△ABC中，内角A，B，C的对边分别为a，b，c，且2a sin B=b．（1）求角A的大小；（2）若a=6，b+c=8，求△ABC的面积．15.（12分）在△ABC中，sin cosA A+=，2AC=，3AB=，求tan A的值和△ABC的面积.16.（12分）在△ABC中，角A，B，C所对的边分别为a ，b ，c ，且tan 21tan A cB b+=． （1）求角A ；（2）若m (0,1)=-，n ()2cos ,2cos 2C B =，试求|m +n |的最小值．1.1正弦定理和余弦定理（人教实验A 版必修5）答题纸得分：一、选择题二、填空题8． 9． 10． 11． 12． 三、解答题 13.14.15.16.1.1正弦定理和余弦定理（人教实验A 版必修5）参考答案1.A 解析：注意余弦定理的形式，特别是正负号问题．2.A 解析：依题意得0°60°，由正弦定理得sin sin a b A B=得sin B ＝sin b A a ＝33，cos B ＝＝63，故选A. 3.D 解析：根据余弦定理，得c 2＝a 2＋b 2－2ab cos C ＝16＋36－2×4×6cos120°＝76，所以c ＝故选D.4.C 解析：由sin 2A －cos 2A ＝12，得cos2A ＝－12，又因为A 是锐角，所以A ＝60°，于是B ＋C ＝120°.所以2b c a+＝sin sin 2sin B C A+2sincos B C B C +-cos2B C -≤1，即b ＋c ≤2a .故选C.5.B 解析：由∠ADB ＝120°，知∠ADC ＝60°.又因为AD ＝2，所以S △ADC ＝12AD ·DC ·sin60°＝3－3，所以DC ＝2(3－1).又因为BD ＝12DC ，所以BD ＝3－1.过A 点作AE ⊥BC 于E 点，则S △ADC ＝12DC ·AE ＝3－3，所以AE ＝ 3.又在直角三角形AED 中，DE ＝1，所以BE ＝ 3.在直角三角形ABE 中，BE ＝AE ，所以△ABE 是等腰直角三角形，所以∠ABC ＝45°. 在直角三角形AEC 中，EC ＝23－3，所以tan ∠ACE ＝AE EC ＝323－3＝2＋3， 所以∠ACE ＝75°，所以∠BAC ＝180°－75°－45°＝60°.故选B.6.C 解析：设等腰三角形的底边长为a ，则由题意知等腰三角形的腰长为2a ，故顶角的余弦值为22244222··a a a a a＋－＝78.故选C. 7.D 解析：由2=，知2=， ∴+，即=0. ∴0，∴.故选D.8.ABD 中，设BD =x ，则2222cos BA BD AD BD AD BDA =+-⋅⋅∠， 即ο60cos 1021014222⋅⋅-+=x x ，整理得096102=--x x ，解得161=x ，62-=x （舍去）. ∵∠ADC =90°，∠BDA =60°，∴∠CDB =30°.由正弦定理得BCD BDCDB BC ∠=∠sin sin ， ∴2830sin 135sin 16=⋅=οοBC . 9.2解析：在△AOB 中，由正弦定理得＝1，∴sin ∠AOB ＝AB . ∵∠AOB =∠，∴.在△A 1OB 1中，由正弦定理得2R ＝＝＝2.10.锐角三角形解析一：根据余弦定理得b 2＝a 2＋c 2－2ac cos B . ∵B ＝60°，2b ＝a ＋c ，∴2a c +⎛⎫⎪⎝⎭2＝a 2＋c 2－2ac cos60°， 整理得(a －c )2＝0，∴a ＝c .∴△ABC 是正三角形．∴△ABC 是锐角三角形． 解析二：根据正弦定理得，2b ＝a ＋c 可转化为2sin B ＝sin A ＋sin C . 又∵B ＝60°，∴A ＋C ＝120°，∴C ＝120°－A ，∴2sin60°＝sin A ＋sin(120°－A )，整理得sin(A ＋30°)＝1， ∴A ＝60°，C ＝60°.∴△ABC 是正三角形．∴△ABC 是锐角三角形． 11.3解析：由正、余弦定理知①③一定成立．对于②，由正弦定理知sin A ＝sin B cos C ＋sin C cos B ＝sin(B ＋C )，显然成立． 对于④，由正弦定理知sin B ＝sin C sin A ＋sin A sin C ＝2sin A sin C ，不一定成立．12.2解析：∵B =2A ，a =1，b =，∴由正弦定理=得： ===， ∴cos A =.由余弦定理得a 2=b 2+c 2-2bc cos A ，即1=3+c 2-3c ， 解得c =2或c =1（经检验不合题意，舍去），则c =2．故填2.13.解：由余弦定理知cos B ＝2222a c b ac＋－，将c ＝a cos B 代入，得c ＝2222a c b ac ＋－，∴c 2＋b 2＝a 2，∴△ABC 是以A 为直角顶点的直角三角形． 又∵b ＝a sin C ，∴b ＝a •ca，∴b ＝c ， ∴△ABC 是等腰三角形．综上所述，△ABC 是等腰直角三角形． 14.解：（1）由2a sin B =b ，利用正弦定理得：2sin A sin B =sin B .∵sin B ≠0，∴sin A =. 又A 为锐角，∴A =.（2）由余弦定理得：a 2=b 2+c 2-2bc cos A ，即36=b 2+c 2-bc =（b +c ）2-3bc =64-3bc ，∴bc =. 又sin A =，则=bc sin A =．15.解法一：先解三角方程，求出角A 的值..21)45cos(,22)45cos(2cos sin =-∴=-=+οοΘA A A A又0180οο<<A ,4560,105.A A ∴-==oootan tan(4560)2A ∴=+=-o o .46260sin 45cos 60cos 45sin )6045sin(105sin sin +=+=+==οοοοοοοA )62(434623221sin 21+=+⨯⨯⨯=•=∴∆A AB AC S ABC . 解法二：由sin cos A A +计算它的对偶关系式sin A -cos A 的值. 22cos sin =+A A Θ，①.0cos ,0sin ,1800.21cos sin 2.21)cos (sin 2<>∴<<-=∴=+∴A A A A A A A οοΘ又23cos sin 21)cos (sin 2=-=-A A A A Θ, 26cos sin =-∴A A .② ①+②，得sin A =+264. ①－②，得cos A =-264.从而sin tan 2cos A A A ===-以下解法同解法一.16.解：（1）由正弦定理得，tan 2sin cos 2sin 11tan sin cos sin A c A B CB b B A B+=⇒+=， 即sin cos sin cos 2sin sin cos sin B A A B CB A B +=， ∴sin()2sin sin cos sin A B CB A B+=， ∴1cos 2A =．∵0πA <<，∴π3A =．（2）∵m +n 2cos ,2cos1(cos ,cos )2C B B C ⎛⎫=-= ⎪⎝⎭， ∴|m +n |222222π1πcos cos cos cos 1sin 2326B C B B B ⎛⎫⎛⎫=+=+-=--⎪ ⎪⎝⎭⎝⎭． ∵π3A =，∴2π3B C +=， ∴2π0,3B ⎛⎫∈ ⎪⎝⎭．从而ππ7π2666B -<-<． ∴当πsin 26B ⎛⎫-⎪⎝⎭＝1，即π3B =时，|m +n |2取得最小值12． ∴|m +n|min =。

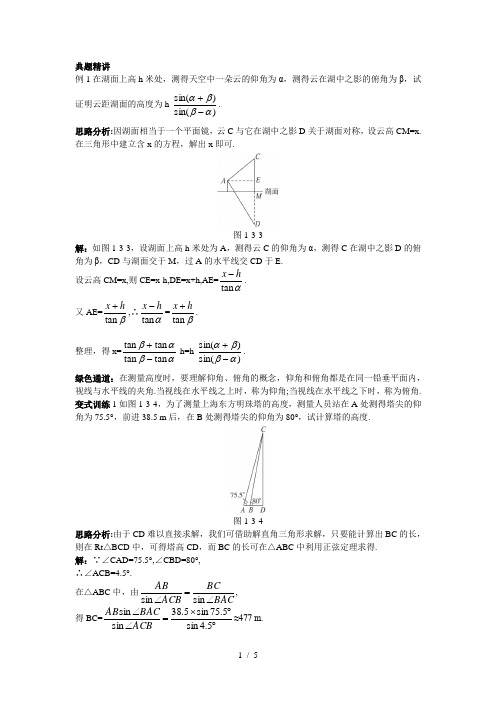
典题精讲例1在湖面上高h 米处，测得天空中一朵云的仰角为α，测得云在湖中之影的俯角为β，试证明云距湖面的高度为h·)sin()sin(αββα-+. 思路分析:因湖面相当于一个平面镜，云C 与它在湖中之影D 关于湖面对称，设云高CM=x. 在三角形中建立含x 的方程，解出x 即可.图1-3-3解：如图1-3-3，设湖面上高h 米处为A ，测得云C 的仰角为α，测得C 在湖中之影D 的俯角为β，CD 与湖面交于M ，过A 的水平线交CD 于E.设云高CM=x,则CE=x-h,DE=x+h,AE=αtan h x -. 又AE=βtan h x +,∴αtan h x -=βtan h x +. 整理，得x=αβαβtan tan tan tan -+·h=h·)sin()sin(αββα-+. 绿色通道：在测量高度时，要理解仰角、俯角的概念，仰角和俯角都是在同一铅垂平面内，视线与水平线的夹角.当视线在水平线之上时，称为仰角;当视线在水平线之下时，称为俯角. 变式训练1如图1-3-4，为了测量上海东方明珠塔的高度，测量人员站在A 处测得塔尖的仰角为75.5°，前进38.5 m 后，在B 处测得塔尖的仰角为80°，试计算塔的高度.图1-3-4思路分析:由于CD 难以直接求解，我们可借助解直角三角形求解，只要能计算出BC 的长，则在Rt △BCD 中，可得塔高CD ，而BC 的长可在△ABC 中利用正弦定理求得.解：∵∠CAD=75.5°,∠CBD=80°,∴∠ACB=4.5°.在△ABC 中，由BACBC ACB AB ∠=∠sin sin , 得BC=︒︒⨯=∠∠5.4sin 5.75sin 5.38sin sin ACB BAC AB ≈477 m.∴CD=BCs in80°≈470 m,即塔的高度为470 m.变式训练2一人见一建筑物A 在正北方向，另一建筑物B 在北偏西30°方向，此人向北偏西70°方向行走3 km 后，则见A 在其北偏东56°方向，B 在其北偏东74°方向，试求这两个建筑物的距离.（精确到10 m ）图1-3-5解：如图1-3-5所示，在△BCO 中，∠BOC=70°-30°=40°,∠BCO=(180°-70°)-74°=36°,∴∠CBO=180°-40°-36°=104°. 由正弦定理，得︒=︒36sin 104sin BO CO . ∴BO=︒︒104sin 36sin 3. 在△AOC 中，∠AOC=70°,∠CAO=56°,∴∠ACO=54°. 由正弦定理，得︒=︒54sin 56sin AO CO . ∴AO=︒︒56sin 54sin 3. 在△AOB 中，由余弦定理,知AB=︒∙∙-+30cos 222BO AO BO AO ≈1 630(m). ∴这两个建筑物的距离为1 630 m.例2如图1-3-6，甲船在A 处，乙船在A 处的南偏东45°方向，距A 有9海里，并以20海里/时的速度沿南偏西15°方向行驶，若甲船以28海里/时的速度行驶，应沿什么方向，用多少小时最快追上乙船？（精确到度）图1-3-6思路分析:假设用t 小时在C 处追上乙船，则在△ABC 中，AC 、BC 可用t 来表示，进而利用余弦定理求得t ，解此三角形即可.解：假设用t 小时，甲船在C 处追上乙船，在△ABC 中，AC=28t,BC=20t,∠ABC=180°-45°-15°=120°.由余弦定理，得AC 2=AB 2+BC 2-2AB·BCcos ∠ABC,即(28t)2=81+(20t)2-2×9×20t×(-21). 整理，得128t 2-60t-27=0,即(4t-3)(32t+9)=0. ∴t=43,t=329-(舍去). ∴AC=28×43=21, BC=20×43=15. 由正弦定理，得sin ∠BAC=1435212315sin =⨯=∠AC ABC BC . 又∠ABC=120°,∴∠BAC 为锐角,∠BAC=38°.∴45°-38°=7°.∴甲船应沿南偏东7°方向用43小时最快追上乙船. 绿色通道：航海问题常利用解三角形的知识去解决，在具体解题时，应画出示意图，找出已知量及所求的量，转化为三角形的边角，利用正弦、余弦定理求解.变式训练在某海滨城市附近海面上有一台风，据监测，当前台风中心位于城市O 的东偏南θ(cosθ=102)方向300 km 的海面P 处，并以20 km/h 的速度向西偏北45°方向移动，台风侵袭的范围为圆形区域，当前半径为60 km ，并以10 km/h 的速度不断增大，问几小时后该城市开始受到台风的侵袭？受影响达多少小时？思路分析:设t 小时后台风中心在Q ，此时城市O 受到台风影响，即此时O 在台风侵袭的圆形区域内，注意台风在行进过程中，其半径在不断地增大，连结OQ ，把问题放到△OPQ 中，利用正弦、余弦定理解三角形即可.图1-3-7解：如图1-3-7，设在t 小时后台风中心在Q 点，此时台风侵袭的圆形区域半径为10t+60（km ）. 若在此刻城市O 受到台风的影响，则OQ≤10t+60.由余弦定理,知OQ 2=PQ 2+PO 2-2PQ·POcos ∠OPQ.由PO=300,PQ=20t,cos ∠OPQ=cos(θ-45°)=cosθcos45°+sinθsin45°=102×22+1-542210212=⨯-. ∴OQ 2=（20t)2+3002-2×20t×300×54=202t 2-9 600t+3002.∴202t 2-9 600t+3002≤(10t+60)2.整理，得t 2-36t+288≤0.解得12≤t≤24.∴12小时后该城市开始受到台风的侵袭，受影响达12小时.例3沿一条小路前进，从A 到B ，方位角是50°，距离是470 m ，从B 到C ，方位角是80°，距离是860 m ，从C 到D ，方位角是150°，距离是640 m.试画出示意图，并计算出从A 到D 的方位角和距离.思路分析:从A 到D 的方位角，需构造三角形，连结AC ，在△ABC 中，用余弦定理求出AC ，进而求出∠BAC,再在△ACD 中，求出AD 和∠CAD.图1-3-8解：示意图如图1-3-8所示，连结AC ，在△ABC 中，∠ABC=50°+(180°-80°)=150°， 由余弦定理，得 AC=︒∙-+150cos 222BC AB BC AB ≈1 289.由正弦定理，得sin ∠BAC=1289150sin 860sin ︒=∠AC ABC BC ≈0.333 6. 利用计算器可得∠BAC≈19.5°,∠ACB=10.5°.在△ACD 中，∠ACD=80°-10.5°+30°=99.5°.由余弦定理，得 AD=ACD CD AC CD AC ∠∙-+cos 222≈1 531.由正弦定理，得∠CAD≈24.4°.∴从A 到D 的方位角为50°+19.5°+24.4°=93.9°,即A 到D 的方位角为93.9°，距离为1 531 m.绿色通道：明确方位角的定义，是由指北方向顺时针到目标方向线的水平角.本题中A 到D 的方位角是50°+∠BAD ，把角的求解放到三角形中，关键是理顺题目中的数量关系，结合示意图，构造出相应的三角形，结合正、余弦定理解决.变式训练A 、B 、C 是一条直路上的三点，AB 与BC 等于1千米.从三点分别望塔P.A 处见塔在东北方，B 处见塔在正东，C 处见塔在南偏东60°.求塔至直路的距离.图1-3-9解：如图1-3-9，由已知条件知∠CPB=30°,∠BPA=45°,AB=BC=1千米.又△CPB 的面积等于△BPA 的面积，故有PB·PAsin45°=PB·PCsin30°⇒PC=2PA. 由△APC 的面积，有PD·AC=PA·PCsin75°⇒PD=22PA 2sin75°. 由余弦定理，有PC 2+PA 2-2PC·PAcos75°=4⇒PA 2=344-. 故PD=22×13357462344+=+⨯-(千米). 问题探究问题两千多年前，我国汉代的天文学家把商高的“测天量地”方法推广到计算太阳的高度.现在我们知道太阳离地球有1 460万千米之遥，可是古代人又能怎样测算呢?导思:把太阳看作一个固定不动的点，选择一根长度已知的标杆，某一时刻找到太阳直射的一个点，再在不同的两个地方把标杆竖起，测量其影子的长度，根据三角形计算就能估算出太阳的高度.探究:那时人们认为天是圆的，地是方的，太阳挂在天空中特定的地方，它的高度是可以测量的.于是，天文学家根据一根已知长度的标杆在不同地方的太阳的影子的长度不同来计算太阳的高度.汉代天文学家把这种计算方法称为“垂差术”.如图1-3-10，设太阳O 垂直照射到地面上的C 点，高度为h ，标杆长为p ，在地方A 的影长为m ，在地方B 的影长为n ，A 到C 的距离为d ，则有图1-3-10 (1)mm d p h +=; (2)nAB n d p h ++=. 解方程组，消去d ，得太阳离地面的高度h=m n pAB -+p.。

解三角形模块一：正余弦定理在△AAA 中的三个内角A ，A ，A 的对边，分别用A ，A ，A 表示． 1．正弦定理：在三角形中，各边的长和它所对的角的正弦的比相等，即A AAA A=A AAA A=A AAA A=2A ．① A =2A AAA A ，A =2A AAA A ，A =2A AAA A ； ② AAA A =A2A ，AAA A =A2A ，AAA A =A2A ； ③ A :A :A =AAA A :AAA A :AAA A ．④ 面积公式：A =12AA AAA A =12AA AAA A =12AA AAA A ． 2．正弦定理用于两类解三角形的问题：① 已知三角形的任意两个角与一边，求其它两边和另一角；② 已知三角形的两边与其中一边的对角，计算另一边的对角，进而计算出其它的边与角． 3．余弦定理：三角形任何一边的平方等于其它两边的平方和减去这两边与它们夹角的余弦的积的两倍，即：{A 2=A 2+A 2−2AA AAA A ,A 2=A 2+A 2−2AA AAA A ,A 2=A 2+A 2−2AA AAA A . 变形式为：{AAA A =A 2+A 2−A 22AA,AAA A =A 2+A 2−A 22AA ,AAA A =A 2+A 2−A 22AA.4．余弦定理及其变形常用来解决这样两类解三角形的问题： ① 已知两边和任意一个内角解三角形； ② 已知三角形的三边解三角形．考点1：正弦定理例1.（1）在ABC ∆中，角A ，B ，C 所对应的边分别为a ，b ，c ．若4A π=，3B π=，a =，则(b = ) A ．1BC ．2D．【解答】解：因为4A π=，3B π=，a =，所以，由正弦定理sin sin a bA B=，可得：2sin sin a B b A ===故选：D ．（2）在ABC ∆中，60A =︒，45B =︒，2b =，则a 等于() AB C ．3D【解答】解：ABC ∆中，60A =︒，45B =︒，2b =，由正弦定理可得，sin sin a bA B=，则2sin sin b Aa B===故选：D ．例2.（1）在ABC∆中，角A ，B ，C 对边分别为a ，b ，c ．已知a =，2A B π-=，则角(C =)A ．12πB ．6π C ．4π D ．3π 【解答】解：在ABC ∆中，角A ，B ，C 对边分别为a ，b ，c ． 已知a ，2A B π-=，则：sin A B =，故：sin()2B B π+，整理得：cos B B ， 所以：tan B =， 由于：0B π<<， 故：6B π=． 2263A πππ=+=， 则：2636C ππππ=--=， 故选：B ．（2）在ABC ∆中，a ，b ，c 分别是角A ，B ，C 22cos c a B +=，则(A = ) A ．6π B ．56π C ．3π D ．23π【解答】22cos c a B +=，2sin 2sin cos B C A B +=， 而sin sin()sin cos cos sin C A B A B A B =+=+，代入化简得2cos sin A B B =， 由于A ，(0,)B π∈，sin 0B ≠，所以cos A =， 可得：56A π=． 故选：B ．例3.（1）满足条件4,45a b A ===︒的三角形的个数是( ) A ．1个B ．2个C ．无数个D ．不存在【解答】解：由余弦定理得2222cos a b c bc A =+-，即216186c c =+-，即2620c c -+=，3c ∴=+3c = 故选：B ．（2）在ABC ∆中，若30A =︒，a 4b =，那么满足条件的(ABC ∆ ) A ．有一个B ．有两个C ．不存在D ．不能确定【解答】解：在ABC ∆中，30A ∠=︒，a =，4b =，∴由余弦定理2222cos a b c bc A =+-，得：2616c =+-，得2100c -+=，(*)△2411080=-⨯⨯=>，且两根之和、两根之积都为正数，∴方程(*)有两个不相等的正实数根，即有两个边c 满足题中的条件，由此可得满足条件的ABC ∆有两个解． 故选：B ．（3）ABC ∆满足下列条件：①3b =，4c =，30B =︒；②5a =，8b =，30A =︒；③6c =，b =60B =︒；④9c =，12b =，60C =︒．其中有两个解的是( )A ．①②B ．①④C ．①②③D ．③④【解答】解：①sin302c ︒=，234b ∴<=<，即sin30c b c ︒<<，因此两解． 同理可得：②两解；③一解，④无解． 故选：A ．考点2：余弦定理例4.（1）ABC ∆中，角A ，B ，C 的对边分别为a ，b ，c ，若b =，4c =．且cos 3cos a B b A =，则ABC ∆的面积为( )A ．2B ．3C ．4D ．【解答】解：ABC ∆中，cos 3cos a B b A =，∴可得：222222322a c b b c a a bac bc+-+-=，整理可得：22222a b c =+，b =，4c =，∴解得：a =222cos2a b c C ab +-==，sin C ∴==，11sin 222ABC S ab C ∆∴===．故选：A ．（2）在ABC ∆中，内角A ，B ，C 所对应的边分别是a ，b ，c ，已知()sin sin sin b c C a A b B +=-，则A ∠的大小为( ) A ．6π B ．3π C ．23π D ．56π 【解答】解：()sin sin sin b c C a A b B +=-，∴已知等式利用正弦定理化简得：22()c c b a b +=-，即222b c a bc +-=-，2221cos 222b c a bc A bc bc +--∴===-，A ∠为三角形内角，23A π∴∠=． 故选：C ．模块二：题型归纳1．解决三角形的综合问题时，要注意以下关系式的运用 ① A +A +A =A ．② AAA (A +A )=AAA A ；AAA (A +A )=−AAA A ． ③ AAAA +A 2=AAA A2；AAAA +A 2=AAA A2．④ A >A ⇔A >A ⇔AAA A >AAA A ． 2．与三角形形状相关的几个结论① 在△AAA 中，若A AAA A =A AAA A ，则△AAA 为等腰三角形或直角三角形； ② 在△AAA 中，若AAAA A =AAAA A =AAAA A ，则△AAA 为等边三角形；③ 在△AAA 中，若AAA 2A +AAA 2A =AAA 2A ，则△AAA 为直角三角形； ④ 在△AAA 中，若A AAA A +A AAA A =A AAA A ，则△AAA 为直角三角形； ⑤ 在△AAA 中，若AAA A (AAA A +AAA A )=AAA A +AAA A ，则△AAA 为直角三角形．考点3：判断三角形形状例5.（1）在ABC ∆中，内角A ，B ，C 的对边分别为a ，b ，c ，若sin b a C =，cos c a B =，则ABC ∆一定是( )A ．等腰三角形非直角三角形B ．直角三角形非等腰三角形C ．等边三角形D ．等腰直角三角形【解答】解：在ABC ∆中，sin b a C =，cos c a B =， 故由正弦定理可得sin sin sin B A C =，sin sin sin C A B =， sin sin sin sin B A A B ∴=，sin 1A ∴=，2A π∴=．sin sin sin C A B ∴= 即sin sin C B =，∴由正弦定理可得c b =，故ABC ∆的形状为等腰直角三角形，故选：D ．（2）在△AAA 中，A =2A AAA A ，则这三角形一定是（ ） A ．等腰三角形B ．直角三角形C ．等腰直角三角形D ．等腰或直角三角形【解答】A（3）在△AAA 中，A 2AAA A =A 2AAA A ，则这三角形一定是（ ） A ．等腰三角形B ．直角三角形C ．等腰直角三角形D ．等腰或直角三角形【解答】D考点4：解决实际问题例6.（1）在一座50m 高的观测台台顶测得对面一水塔塔顶仰角为60︒，塔底俯角为45︒，那么这座塔的高为( ) A．50(1 m B．50(1+ m C． m D． m【解答】解：如图，由已知可得：50AD DC m ==，tan 60BD AD ∴=︒=，∴塔高为50(1CD BD m +=+．故选：B ．（2）如图，A ，A 是海面上位于东西方向相距5(3+√3)海里的两个观测点，现位于A 点北偏东45°，A 点北偏西60°的A 点有一艘轮船发出求救信号，位于A 点南偏西60°且与点A 相距20√3海里的A 点的救援船立即前往营救，其航行速度为30海里/小时，该救援船达到A 点需要多长时间 【解答】1小时考点5：正余弦定理综合应用例7.（1）在ABC ∆中，角A ，B ，C 的对边分别为a ，b ，c ，2222sin bc A b c a =+-，ABC ∆的外，则a 的值为( )A ．1B ．2C D ．【解答】解：2222sin 2cos bc A b c a bc A =+-=， sin cos A A ∴=，即tan 1A =，4A π∴=，ABC ∆的外接圆半径r =则由正弦定理可得，2sin ar A== 2a ∴=．故选：B ．（2）在ABC ∆中，已知三个内角为A ，B ，C 满足sin :sin :sin 3:5:7A B C =，则(C = ) A ．90︒B ．120︒C ．135︒D ．150︒【解答】解：由正弦定理知2sin sin sin a b cR A B C===， sin 2a A R ∴=，sin 2b B R =，sin 2cC R=，sin :sin :sin 3:5:7A B C =， ::3:5:7a b c ∴=，设3a t =，5b t =，7c t =，222222925491cos 22352a b c t t t C ab t t +-+-∴===-⨯⨯，0180C ︒<<︒， 120C ∴=︒．故选：B ．（3）已知ABC ∆的面积为，角A ，B ，C 的对边分别为a ，b ，c ，若14b =，(2)cos cos 0a c B b A ++=，则(a c += )A ．16B ．12C ．8D ．4【解答】解：(2)cos cos 0a c B b A ++=，(sin 2sin )cos sin cos 0A C B B A ∴++=，可得：(sin cos sin cos )2sin cos 0A B B A C B ++=，可得：sin()2cos sin 0A B B C ++=， 可得：sin()sin A B C +=， 1cos 2B ∴=-，23B π∴=．14b =，ABC ∆的面积为132ac，可得：60ac =， ∴由余弦定理可得：2222196()()60a c ac a c ac a c =++=+-=+-，解得：16a c +=．故选：A ．（4）在ABC ∆中，3A π=，2b =，其面积为sin sin A Ba b++等于( )A ．14B ．13C D【解答】解：由题意可得：11sin 222ABC S bc A c ∆==⨯⨯=解得：4c =，根据余弦定理有：22212cos 416224122a b c bc A =+-=+-⨯⨯⨯=，所以，a =根据正弦定理2sin sin sin a b cR A B C ===，则：sin sin sin sin 1sin 12(sin sin )24A B A B A a b R A B R a ++=====++， 故选：A ．课后作业：1.ABC∆的内角A，B，C的对边分别为a，b，c，若4cos5A=，5cos13C=，13a=，则(b=)A．12 B．42 C．21 D．63【解答】解：由4cos5A=，5cos13C=，可得3sin5A==，12sin13C，3541263sin sin()sin cos cos sin51351365B AC A C A C=+=+=⨯+⨯=，由正弦定理可得6313sin65213sin5a BbA⨯===．故选：C．2.在ABC∆中，a，b，c分别是角A，B，C22cosc a B+=，则(A=)A．6πB．56πC．3πD．23π【解答】22cosc a B+=，2sin2sin cosB C A B+=，而sin sin()sin cos cos sinC A BA B A B=+=+，代入化简得2cos sinA B B=，由于A，(0,)Bπ∈，sin0B≠，所以cos A=，可得：56Aπ=．故选：B．3.ABC∆满足下列条件：①3b=，4c=，30B=︒；②5a=，8b=，30A=︒；③6c=，b=，60B=︒；④9c=，12b=，60C=︒．其中有两个解的是()A．①②B．①④C．①②③D．③④【解答】解：①sin302c ︒=，234b ∴<=<，即sin30c b c ︒<<，因此两解． 同理可得：②两解；③一解，④无解． 故选：A ．4.在ABC ∆中，内角A ，B ，C 所对应的边分别是a ，b ，c ，已知()sin sin sin b c C a A b B +=-，则A ∠的大小为( )A ．6π B ．3π C ．23π D ．56π 【解答】解：()sin sin sin b c C a A b B +=-，∴已知等式利用正弦定理化简得：22()c c b a b +=-，即222b c a bc +-=-，2221cos 222b c a bc A bc bc +--∴===-，A ∠为三角形内角，23A π∴∠=． 故选：C ．5.）在ABC ∆中，3A π=，2b =，其面积为sin sin A Ba b++等于( )A ．14B ．13C D【解答】解：由题意可得：11sin 222ABC S bc A c ∆==⨯⨯=解得：4c =，根据余弦定理有：22212cos 416224122a b c bc A =+-=+-⨯⨯⨯=，所以，a =根据正弦定理2sin sin sin a b cR A B C ===，则：sin sin sin sin 1sin 12(sin sin )24A B A B A a b R A B R a ++=====++， 故选：A ．。

数学必修5解三角形-正弦-余弦知识点和练习题(含答案)解三角形1．正弦定理:2sin sin sin a b cR A B C===或变形：::sin :sin :sin a b c A B C=.2．余弦定理： 2222222222cos 2cos 2cos a b c bc A b a c ac B c b a ba C ⎧=+-⎪=+-⎨⎪=+-⎩或222222222cos 2cos 2cos 2b c a A bc a c b B ac b a c C ab ⎧+-=⎪⎪+-⎪=⎨⎪⎪+-=⎪⎩.3．（1）两类正弦定理解三角形的问题：1、已知两角和任意一边，求其他的两边及一角.2、已知两角和其中一边的对角，求其他边角.（2）两类余弦定理解三角形的问题：1、已知三边求三角.2、已知两边和他们的夹角，求第三边和其他两角.4．判定三角形形状时，可利用正余弦定理实现边角转化，统一成边的形式或角的形式.5．解题中利用ABC ∆中A B C π++=，以及由此推得的一些基本关系式进行三角变换的运算，如：sin()sin ,A B C +=cos()cos ,A B C +=-tan()tan ,A B C +=-sin cos ,cos sin ,tan cot 222222A B C A B C A B C +++===.、已知条件定理应用一般解法一边和两角（如a、B、C）正弦定理由A+B+C=180˙，求角A，由正弦定理求出b与c，在有解时有一解。

两边和夹角(如a、b、c)余弦定理由余弦定理求第三边c，由正弦定理求出小边所对的角，再由A+B+C=180˙求出另一角，在有解时有一解。

三边(如a、b、c)余弦定理由余弦定理求出角A、B，再利用A+B+C=180˙，求出角C在有解时只有一解。

1、ΔABC中,a=1,b=3, ∠A=30°,则∠B等于（）A．60°B．60°或120°C．30°或150°D．120°2、符合下列条件的三角形有且只有一个的是（）A．a=1,b=2 ,c=3 B．a=1,b=2,∠A=30°8、A 为ΔABC 的一个内角,且sinA+cosA=127, 则ΔABC 是______三角形.9、在ΔABC 中，若S ΔABC =41 (a 2+b 2－c 2),那么角∠C=______.10、在ΔABC 中，a =5,b = 4,cos(A －B)=3231,则cosC=_______.11、在ΔABC 中,求分别满足下列条件的三角形形状： ①B=60°,b 2=ac ； ②b 2tanA=a 2tanB ；③sinC=BA B A cos cos sin sin ++④ (a 2－b 2)sin(A+B)=(a 2+b 2)sin(A －B).12． 在ABC △中，已知内角A π=3，边3BC =B x =，周长为y ．（1）求函数()y f x =的解析式和定义域；（2）求y 的最大值． 13． 在ABC中，角,,A B C 对应的边分别是,,a b c ，若1sin ,2A =3sin 2B =，求::a b c14． 在ABC中,,a b c分别为,,A B C∠∠∠的对边，若2sin (cos cos )3(sin sin )A B C B C +=+，（1）求A 的大小；（2）若61,9a b c =+=，求b 和c 的值。

高中数学必修五三角函数知识点+练习题含答案解析(很详细)第一部分必修五三角函数知识点整理第一章解三角形1、三角形的性质：①.A+B+C=π,? 222A B C π+=-?sin cos 22A B C += ②.在ABC ?中, a b +＞c , a b -＜c ; A ＞B ?sin A ＞sinB ...........................A ＞B ?cosA ＜cosB, a ＞b ? A ＞B③.若ABC ?为锐角?，则A B +＞2π,B+C ＞2π,A+C ＞2π; 22a b +＞2c ，22b c +＞2a ，2a ＋2c ＞2b2、正弦定理与余弦定理：①.(2R 为ABC ?外接圆的直径)2s i n a R A =、2sin b R B =、2sin c R C =sin 2a A R =、 sin 2b B R =、 sin 2c C R= 面积公式：111sin sin sin 222ABC S ab C bc A ac B ?=== ②.余弦定理：2222cos a b c bc A =+-、2222cos b a c ac B =+-、2222cos c a b ab C =+-222cos 2b c a A bc +-=、222cos 2a c b B ac +-=、222cos 2a b c C ab+-= 补充：两角和与差的正弦、余弦和正切公式：⑴()cos cos cos sin sin αβαβαβ-=+；⑵()cos cos cos sin sin αβαβαβ+=-；⑶()sin sin cos cos sin αβαβαβ-=-；⑷()sin sin cos cos sin αβαβαβ+=+；⑸()tan tan tan 1tan tan αβαβαβ --=+ ? （()()tan tan tan 1tan tan αβαβαβ-=-+）；⑹()tan tan tan 1tan tan αβαβαβ++=- ? （()()tan tan tan 1tan tan αβαβαβ+=+-）．二倍角的正弦、余弦和正切公式：⑴sin 22sin cos ααα=．222)cos (sin cos sin 2cos sin 2sin1ααααααα±=±+=±?⑵2222cos2cos sin 2cos 112sin ααααα=-=-=-升幂公式2sin 2cos 1,2cos 2cos 122αααα=-=+ ?落幂公式2cos 21cos 2αα+=，21cos 2sin 2αα-=．第二部分必修五练习题含答案解析第一章解三角形1.在△ABC 中，AB ＝5，BC ＝6，AC ＝8，则△ABC 的形状是( )A ．锐角三角形B ．直角三角形C ．钝角三角形D ．非钝角三角形解析：最大边AC 所对角为B ，则cosB ＝52＋62－822×5×6＝－320B>CB ．B>A>C C ．C>B>AD ．C>A>B解析由正弦定理a sinA ＝b sinB ，∴sinB ＝bsinA a ＝32.∵B 为锐角，∴B ＝60°，则C ＝90°，故C>B>A. 答案 C3．在△ABC 中，已知a ＝8，B ＝60°，C ＝75°，则b 等于( )A ．4 2B ．4 3C ．4 6 D.323解:由A ＋B ＋C ＝180°，可求得A ＝45°，由正弦定理，得b ＝asinB sinA ＝8×sin60°sin45°＝8×3222＝4 6. 答案 C4．在△ABC 中，AB ＝5，BC ＝7，AC ＝8，则BA →·BC → 的值为( )A ．5B ．－5C ．15D ．－15解析在△ABC 中，由余弦定理得：cosB ＝AB 2＋BC 2－AC 22AB ·BC ＝25＋49－642×5×7＝17. ∴BA →·BC →＝|BA →|·|BC →|cosB ＝5×7×17＝5. 答案 A5．若三角形三边长之比是1：3：2，则其所对角之比是( )A ．1：2：3B ．1：3：2C ．1：2： 3 D.2：3：2解析设三边长分不为a ，3a,2a ，设最大角为A ，则cosA ＝a 2＋3a 2－2a 22·a ·3a ＝0，∴A ＝90°.设最小角为B ，则cosB ＝2a 2＋3a 2－a 22·2a ·3a ＝32，∴B ＝30°，∴C ＝60°. 所以三角之比为1：2：3. 答案 A6．在△ABC 中，若a ＝6，b ＝9，A ＝45°，则此三角形有( )A ．无解B ．一解C ．两解D ．解的个数别确定解析由b sinB ＝a sinA ，得sinB ＝bsinA a ＝9×226＝3 24>1.∴此三角形无解．答案 A7．已知△ABC 的外接圆半径为R ，且2R(sin 2A －sin 2C)＝(2a －b)sinB(其中a ，b 分不为A ，B 的对边)，这么角C 的大小为( )A ．30°B ．45°C ．60°D ．90°解析依照正弦定理，原式可化为2R ? ??a 24R 2－c 24R 2＝(2a －b)·b 2R ，∴a 2－c 2＝(2a －b)b ，∴a 2＋b 2－c 2＝2ab ，∴cosC ＝a 2＋b 2－c 22ab ＝22，∴C ＝45°. 答案 B8．在△ABC 中，已知sin 2A ＋sin 2B －sinAsinB ＝sin 2C ，且满脚ab ＝4，则该三角形的面积为( )A ．1B ．2 C. 2 D. 3解析由a sinA ＝b sinB ＝c sinC＝2R ，又sin 2A ＋sin 2B －sinAsinB ＝sin 2C ，可得a 2＋b 2－ab ＝c 2.∴c osC ＝a 2＋b 2－c 22ab ＝12，∴C ＝60°，sinC ＝32. ∴S △ABC ＝12absinC ＝ 3. 答案 D9．在△ABC 中，A ＝120°，AB ＝5，BC ＝7，则sinB sinC 的值为( ) A.85 B.58 C.53 D.35解析由余弦定理，得 cosA ＝AB 2＋AC 2－BC 22AB ·AC，解得AC ＝3. 由正弦定理sinB sinC ＝AC AB ＝35. 答案 D10.在三角形ABC 中，AB ＝5，AC ＝3，BC ＝7，则∠BAC 的大小为( )A.2π3B.5π6C.3π4D.π3解析由余弦定理，得cos ∠BAC ＝AB 2＋AC 2－BC 22AB ·AC ＝52＋32－722×5×3＝－12，∴∠BAC ＝2π3. 答案 A11．有一长为1 km 的歪坡，它的倾歪角为20°，现要将倾歪角改为10°，则坡底要加长( )A ．0.5 kmB ．1 kmC ．1.5 km D.32km 解析如图，AC ＝AB ·sin20°＝sin20°，BC ＝AB ·cos20°＝cos20°，DC ＝AC tan10°＝2cos 210°，∴DB ＝DC －BC ＝2cos 210°－cos20°＝1.答案 B12．已知△ABC 中，A ，B ，C 的对边分不为a ，b ，c.若a ＝c ＝6＋2，且A ＝75°，则b 为( )A ．2B ．4＋2 3C ．4－2 3 D.6－ 2解析在△ABC 中，由余弦定理，得a 2＝b 2＋c 2－2bccosA ，∵a ＝c ，∴0＝b 2－2bccosA ＝b 2－2b(6＋2)cos75°，而cos75°＝cos(30°＋45°)＝cos30°cos45°－sin30°sin45°＝22? ????32－12＝14(6－2)，∴b 2－2b(6＋2)cos75°＝b 2－2b(6＋2)·14(6－2)＝b 2－2b ＝0，解得b ＝2，或b ＝0(舍去)．故选A. 答案 A 13．在△ABC 中，A ＝60°，C ＝45°，b ＝4，则此三角形的最小边是____________．解析由A ＋B ＋C ＝180°，得B ＝75°，∴c 为最小边，由正弦定理，知c ＝bsinC sinB ＝4sin45°sin75°＝4(3－1)．答案 4(3－1)14．在△ABC 中，若b ＝2a ，B ＝A ＋60°，则A ＝________.解析由B ＝A ＋60°，得 sinB ＝sin(A ＋60°)＝12sinA ＋32cosA. 又由b ＝2a ，知sinB ＝2sinA.∴2sinA ＝12sinA ＋32cosA. 即32sinA ＝32cosA.∵cosA ≠0，∴tanA ＝33.∵0°<A<180°，∴A ＝30°. 答案30° 15．在△ABC 中，A ＋C ＝2B ，BC ＝5，且△ABC 的面积为103，则B ＝_______，AB ＝_______.解析由A ＋C ＝2B 及A ＋B ＋C ＝180°，得B ＝60°.又S ＝12AB ·BC ·sinB ，∴10 3＝12AB ×5×sin60°，∴AB ＝8. 答案60° 816．在△ABC 中，已知(b ＋c)：(c ＋a)：(a ＋b)＝8：9：10，则sinA ：sinB ：sinC ＝________.解析设b ＋c ＝8k ，c ＋a ＝9k ，a ＋b ＝10k ，可得a ：b ：c ＝11：9：7.∴sinA ：sinB ：sinC ＝11：9：7.答案 11：9：717．在非等腰△ABC 中，角A ，B ，C 所对的边分不为a ，b ，c ，且a 2＝b(b ＋c)．(1)求证：A ＝2B ；(2)若a ＝XXX ，试推断△ABC 的形状．解 (1)证明：在△ABC 中，∵a 2＝b ·(b ＋c)＝b 2＋bc ，由余弦定理，得cosB ＝a 2＋c 2－b 22ac ＝bc ＋c 22ac ＝b ＋c 2a ＝a 2b ＝sinA 2sinB ，∴sinA ＝2sinBcosB ＝sin2B.则A ＝2B 或A ＋2B ＝π.若A ＋2B ＝π，又A ＋B ＋C ＝π，∴B ＝C.这与已知相矛盾，故A ＝2B.(2)∵a ＝XXX ，由a 2＝b(b ＋c)，得XXX 2＝b 2＋bc ，∴c ＝2b.又a 2＋b 2＝4b 2＝c 2.故△ABC 为直角三角形．18．锐角三角形ABC 中，边a ，b 是方程x 2－23x ＋2＝0的两根，角A ，B 满脚2sin(A ＋B)－3＝0.求：(1)角C 的度数；(2)边c 的长度及△ABC 的面积．解 (1)由2sin(A ＋B)－3＝0，得sin(A ＋B)＝32. ∵△ABC 为锐角三角形，∴A ＋B ＝120°，∴∠C ＝60°.(2)∵a ，b 是方程x 2－23x ＋2＝0的两个根，∴a ＋b ＝23，ab ＝2.∴c 2＝a 2＋b 2－2abcosC ＝(a ＋b)2－3ab ＝12－6＝6.∴c ＝ 6.S △ABC ＝12absinC ＝12×2×32＝32. 19.已知△ABC 的角A ，B ，C 所对的边分不是a ，b ，c ，设向量m ＝(a ，b)，n ＝(sinB ，sinA)，p ＝(b －2，a －2)．(1)若m ∥n ，求证：△ABC 为等腰三角形；(2)若m ⊥p ，边长c ＝2，角C ＝π3，求△ABC 的面积．解 (1)证明：∵m ∥n ，∴asinA ＝bsinB.由正弦定得知，sinA ＝a 2R ，sinB ＝b 2R (其中R 为△ABC 外接圆的半径)，代入上式，得a ·a 2R ＝b ·b 2R，∴a ＝b.故△ABC 为等腰三角形．(2)∵m ⊥p ，∴m ·p ＝0，∴a(b －2)＋b(a －2)＝0，∴a ＋b ＝ab.由余弦定理c 2＝a 2＋b 2－2abcosC 得4＝(a＋b)2－3ab，即(ab)2－3ab－4＝0. 解得ab＝4，ab＝－1(舍去)．∴△ABC的面积S＝12absinC＝12×4×sinπ3＝ 3.。

人教版高中数学必修5正弦定理和余弦定理测试题及答案时间：2021.02.05 创作：欧阳科一、选择题1．在△ABC中，三个内角A，B，C的对边分别是a，b，c，若a＝2，b＝3，cos C＝－，则c等于( )(A)2 (B)3 (C)4 (D)52．在△ABC中，若BC＝，AC＝2，B＝45°，则角A等于( )(A)60°(B)30°(C)60°或120°(D)30°或150°3．在△ABC中，三个内角A，B，C的对边分别是a，b，c，已知B＝30°，c＝150，b＝50，那么这个三角形是( )(A)等边三角形(B)等腰三角形(C)直角三角形(D)等腰三角形或直角三角形4．在△ABC中，已知，AC＝2，那么边AB 等于( )(A)(B)(C)(D)5．在△ABC中，三个内角A，B，C的对边分别是a，b，c，如果A∶B∶C＝1∶2∶3，那么a∶b∶c等于( )(A)1∶2∶3 (B)1∶∶2 (C)1∶4∶9 (D)1∶∶二、填空题6．在△ABC中，三个内角A，B，C的对边分别是a，b，c，若a＝2，B＝45°，C＝75°，则b＝________.7．在△ABC中，三个内角A，B，C的对边分别是a，b，c，若a＝2，b＝2，c＝4，则A＝________.8．在△ABC中，三个内角A，B，C的对边分别是a，b，c，若2cos B cos C＝1－cos A，则△ABC形状是________三角形.9．在△ABC中，三个内角A，B，C的对边分别是a，b，c，若a＝3，b＝4，B＝60°，则c＝________.10．在△ABC中，若tan A＝2，B＝45°，BC＝，则AC＝________.三、解答题11．在△ABC中，三个内角A，B，C的对边分别是a，b，c，若a＝2，b＝4，C＝60°，试解△ABC.12．在△ABC中，已知AB＝3，BC＝4，AC＝.(1)求角B的大小；(2)若D是BC的中点，求中线AD的长.13．如图，△OAB的顶点为O(0，0)，A(5，2)和B(－9，8)，求角A的大小.14．在△ABC中，已知BC＝a，AC＝b，且a，b是方程x2－2x＋2＝0的两根，2cos(A＋B)＝1.(1)求角C的度数；(2)求AB的长；(3)求△ABC的面积.参考答案一、选择题1． C 2．B 3．D 4．B 5．B提示：4．由正弦定理，得sin C＝，所以C＝60°或C＝120°，当C＝60°时，∵B＝30°，∴A＝90°，△ABC是直角三角形；当C＝120°时，∵B＝30°，∴A＝30°，△ABC是等腰三角形.5．因为A∶B∶C＝1∶2∶3，所以A＝30°，B＝60°，C＝90°，由正弦定理＝k，得a＝k·sin30°＝k，b＝k·sin60°＝k，c＝k·sin90°＝k，所以a∶b∶c＝1∶∶2.二、填空题6． 7．30° 8．等腰三角形 9． 10．提示：8．∵A＋B＋C＝π，∴－cos A＝cos(B＋C).∴2cos B cos C＝1－cos A＝cos(B＋C)＋1，∴2cos B cos C＝cos B cos C－sin B sin C＋1，∴cos(B－C)＝1，∴B－C＝0，即B＝C.9．利用余弦定理b2＝a2＋c2－2ac cos B.10．由tan A＝2，得，根据正弦定理，得，得AC＝.三、解答题11．c＝2，A＝30°，B＝90°.12．(1)60°；(2)AD＝.13．如右图，由两点间距离公式，得OA＝，同理得.由余弦定理，得cos A＝，∴A＝45°.14．(1)因为2cos(A＋B)＝1，所以A＋B＝60°，故C＝120°.(2)由题意，得a＋b＝2，ab＝2，又AB2＝c2＝a2＋b2－2ab cos C＝(a＋b)2－2ab－2ab cos C＝12－4－4×()＝10.所以AB＝.(3)S△ABC＝ab sin C＝·2·＝.时间：2021.02.05 创作：欧阳科。