固体火箭发动机燃烧室及内弹道计算

!计?算?星?型³装痢?药?的?几?何?尺?寸?!参?数簓符?号?说μ明¶!-----------------------------------------------------------------------------------!n表括?示?星?角?数簓,num表括?示?将?推?进?剂®沿?肉╝厚?方?向´分?为a几?等台?分?,m表括?示?选?择?压1力 值μ大洙?小?!d表括?示?外猘径?,len表括?示?长¤度¯,thet表括?示?星?边?夹D角?,epsilon表括?示?角?度¯系μ数簓!r表括?示?过y度¯圆2弧?半?径?,r1表括?示?星?角?圆2弧?半?径?,R0表括?示?通 ?用?气?体?常￡数簓!l表括?示?药?柱·的?特?征¶长¤度¯,y0表括?示?初?始?特?征¶参?数簓,y1表括?示?燃?尽?特?征¶参?数簓!I0表括?示?总哩?冲?,F表括?示?推?力 ,Poc表括?示?燃?烧?室酣?的?工¤作痢?压1力!Isp表括?示?比括?冲?,density_p表括?示?密¹度¯,k表括?示?比括?热¯?比括?rspeed表括?示?燃?速·，?pn表括?示?压1力 指?数簓!mpeff表括?示?有瓺效§装痢?药?量?,Cf表括?示?推?力 系μ数簓,Ctz表括?示?特?征¶速·度¯,At表括?示?喉³部?面?积y,a表括?示?燃?速·系μ数簓!S表括?示?平?均·燃?烧?面?积y,e1表括?示?平?均·肉╝厚?,epsilon1表括?示?减?面?比括?epsilon2表括?示?增?面?比括?!foresmax表括?示?前©段?最?大洙?相­对?周¹边?长¤,backsmax表括?示?后µ段?最?大洙?相­对?周¹边?长¤!smin表括?示?最?小?相­对?周¹边?长¤,thet1表括?示?周¹边?长¤取?得?最?小?值μ时骸?的?星?边?夹D角?!Ap表括?示?初?始?通 ?气?面?积y,J表括?示?初?始?通 ?气?参?量?,eta表括?示?装痢?填?系μ数簓,Af表括?示?剩骸?药?面?积y,etaf表括?示?剩骸?药?系μ数簓!de表括?示?每?一?份 肉╝厚?的?长¤度¯,Sa表括?示?燃?烧?面?积y数簓组哩?Apa表括?示?通 ?气?面?积y数簓组哩?!------------------------------------------------------------------------------------program mainimplicit nonereal(kind=8),parameter :: Pi=3.14integer :: n,num,i,mreal(kind=8) :: d,len,thet,epsilon,r,r1real(kind=8) :: l,y0,y1real(kind=8) :: I0,F,Poc,Pe,R0real(kind=8) :: Isp,density_p,k,rspeed,Pnreal(kind=8) :: mpeff,Cf,Ctz,At,areal(kind=8) :: S,e1,epsilon1,epsilon2real(kind=8) :: foresmax,backsmax,smin,thet1real(kind=8) :: Ap,J,eta,Af,etafreal(kind=8) :: error,dereal(kind=8),allocatable :: Sa(:),Apa(:)!读®入?所·需¯要癮所·用?参?数簓值μopen(3,file="design_parameter.dat")read(3,*) I0 !总哩?冲?read(3,*) F !推?力read(3,*) Poc !燃?烧?室酣?压1力read(3,*) Isp !比括?冲?read(3,*) density_p !推?进?剂®的?密¹度¯read(3,*) k !比括?热¯?比括?read(3,*) a !燃?速·系μ数簓read(3,*) Ctz !读®取?特?征¶速·度¯Ctzread(3,*) Pn !压1力 指?数簓read(3,*) Pe !读®取?喷?管¹出?口¸的?压1力 Peread(3,*) R0 !读®取?通 ?用?气?体?常￡数簓R0read(3,*) d,r !读®取?装痢?药?直ª径?d和³过y度¯圆2弧?半?径?rread(3,*) epsilon2 !读®取?增?面?比括╡psilon2read(3,*) r1 !读®取?星?角?圆2弧?半?径?r1read(3,*) thet1 !试?取?周¹边?长¤取?得?最?小?值μ时骸?的?星?边?夹D角?thet1read(3,*) thet !试?取?初?始?时骸?的?星?边?夹D角?thetread(3,*) n !读®取?星?角?数簓n（辍?,4,5,6,7,8）?read(3,*) epsilon !试?取?角?度¯系μ数簓epsilonread(3,*) num !读®取?等台?分?肉╝厚?的?等台?分?数簓numread(3,*) m !m=1表括?示?最?小?压1力 给?定¨,m=2表括?示?最?大洙?压1力 给?定¨,m=0表括?示?平?均·压1力 给?定¨close(3)allocate(Sa(0:num),Apa(0:num))!根·据Y规?定¨的?总哩?冲?计?算?有瓺效§装痢?药?量?mpeffmpeff=1.02*I0/Isp!计?算?推?力 系μ数簓和³喉³部?面?积yCf=sqrt(k)*(2/(k+1))**((k+1)/(k-1)/2)*sqrt(2*k*(1-(Pe/Poc)**((k-1)/k))/(k-1))At=F/Cf/(Poc*101325.0)!计?算?平?均·肉╝厚?e1和³计?算?特?征¶长¤度¯和³平?均·燃?烧?面?积yS!若?给?定¨的?是?最?大洙?压1力 则´需¯根·据Y增?面?比括?计?算?最?小?燃?面?再·计?算?平?均·燃?面?值μ!y1一?般?取?值μ在¸1附?近¹,(0.8-1.2)if(m==0) then!平?均·压1力 给?定¨S=At*(Poc*101325.0)**(1-Pn)/(Ctz*density_p*a)e1=mpeff/(density_p*S)else if(m==1) then!最?小?压1力 给?定¨S=At*(Poc*101325.0)**(1-Pn)/(Ctz*density_p*a)S=(epsilon2+1.0)*S/2.0e1=mpeff/(density_p*S)else!最?大洙?压1力 给?定¨S=At*(Poc*101325.0)**(1-Pn)/(Ctz*density_p*a)S=(1.0/epsilon2+1.0)*S/2.0e1=mpeff/(density_p*S)end ifl=d/2-e1-ry0=r/ly1=(e1+r)/l!根·据Yepsilon2选?择?角?度¯系μ数簓epsilon!计?算?取?得?最?小?周¹长¤时骸?的?thet1do while(.true.)error=thet1/2+cotan(thet1/2)-Pi/n-Pi/2if(error>=0.0001) thenthet1=thet1+0.00001else if(error<=-0.0001) thenthet1=thet1-0.00001elseexitend ifend do!计?算?角?度¯系μ数簓epsilon的?准?确º?值μdo while(.true.)backsmax=2*n*((1-epsilon)*Pi/n+y1*(Pi/n+asin(sin(epsilon*Pi/n)/y1))) smin=2*n*(sin(epsilon*Pi/n)/sin(thet1/2)+(1-epsilon)*Pi/n) if(backSmax/Smin>epsilon2) thenepsilon=epsilon+0.001elseexitend ifend do!根·据Y减?面?比括╡psilon1，?计?算?thetepsilon1=1/epsilon2foresmax=smin/epsilon1do while(.true.)error=2*n*(sin(epsilon*Pi/n)/sin(thet/2)+(1-epsilon)*Pi/n+&(r1+r)*(Pi/n+Pi/2-thet/2-cos(thet/2)/sin(thet/2))/l)-foresmax if(error>=0.0001) thenthet=thet+0.00001else if(error<=-0.0001) thenthet=thet-0.00001elseexitend do!计?算?初?始?通 ?气?面?积y，?通 ?气?参?量?，?装痢?填?系μ数簓,药?柱·长¤度¯Ap=(n*((1-epsilon)*Pi/n+sin(epsilon*Pi/n)*(cos(epsilon*Pi/n)-&sin(epsilon*Pi/n)*cotan(thet/2)))+2*n*r*(sin(epsilon*Pi/n)/sin(thet/2)+&(1-epsilon)*Pi/n)/l+n*r**2*(Pi/n+Pi/2-thet/2-cotan(thet/2))/l**2+&n*r1**2*(thet/2+cotan(thet/2)-Pi/2)/l**2)*l**2J=At/Apeta=4*(Pi*d**2/4-Ap)/(Pi*d**2)Af=(epsilon*Pi*(1+y1)**2-n*(sin(epsilon*Pi/n)*(sqrt(y1**2-sin(epsilon*Pi/n)**2)+& cos(epsilon*Pi/n)))-n*y1**2*(epsilon*Pi/n+asin(sin(epsilon*Pi/n)/y1)))*l**2etaf=4*Af/(pi*d**2)len=mpeff/density_p/(Pi*d**2/4-Ap-Af)!计?算?推?进?剂®的?燃?面?变?化ˉ规?律°并￠输?出?结®果?de=e1/numopen(10,file="export_burnS.dat")open(20,file="export_Ap.dat")do i=0,num,1if((i*de)<=r1) thenSa(i)=2*n*(sin(epsilon*Pi/n)/sin(thet/2)+(1-epsilon)*Pi/n+&(r1+r)*(Pi/n+Pi/2-thet/2-cotan(thet/2))/l-(r1-i*de)*Pi/n/l)*l*len Apa(i)=(n*((1-epsilon)*Pi/n+sin(epsilon*Pi/n)*(cos(epsilon*Pi/n)-sin(epsilon*Pi/n)* cotan(thet/2)))+&2*n*(r+i*de)*(sin(epsilon*Pi/n)/sin(thet/2)+(1-epsilon)*Pi/n)/l+&n*(r+i*de)**2*(Pi/n+Pi/2-thet/2-cotan(thet/2))/l**2+n*(r1-i*de)**2*(thet/2+cotan(thet/2 )-Pi/2)/l**2)*l**2else if((i*de)>r1.and.(i*de)<=(l*sin(epsilon*Pi/n)/cos(thet/2)-r)) thenSa(i)=2*n*(sin(epsilon*Pi/n)/sin(thet/2)+(1-epsilon)*Pi/n+&(i*de+r)*(Pi/n+Pi/2-thet/2-cotan(thet/2))/l)*l*lenApa(i)=(n*((1-epsilon)*Pi/n+sin(epsilon*Pi/n)*(cos(epsilon*Pi/n)-sin(epsilon*Pi/n)* cotan(thet/2)))+&2*n*(r+i*de)*(sin(epsilon*Pi/n)/sin(thet/2)+(1-epsilon)*Pi/n)/l+&n*(r+i*de)**2*(Pi/n+Pi/2-thet/2-cotan(thet/2))/l**2)*l**2else if((i*de)>(l*sin(epsilon*Pi/n)/cos(thet/2)-r).and.(i*de)<=e1) thenSa(i)=2*n*((1-epsilon)*Pi/n+(r+i*de)*(Pi/n+asin(l*sin(epsilon*Pi/n)/(i*de+r)))/l)*l *lenApa(i)=n*((1-epsilon)*Pi*(1+(r+i*de)/l)**2/n+sin(epsilon*Pi/n)*(sqrt((r+i*de)**2/l* *2-&sin(epsilon*Pi/n)**2)+cos(epsilon*Pi/n))+(r+i*de)**2*(epsilon*Pi/n+&asin(l*sin(epsilon*Pi/n)/(r+i*de)))/l**2)*l**2write(10,"(f10.5,2X,f15.5)") i*de,Sa(i)write(20,"(f10.5,2X,f15.5)") i*de,Apa(i)end doclose(10)close(20)!调獭?用?子哩?程²序´计?算?装痢?药?内¸弹獭?道台?曲¸线?callinternal_ballistics0(d,len,e1,n,thet,epsilon,r,r1,l,a,pn,Ctz,At,k,density_p,mpeff,Isp) !输?出?星?型³装痢?药?的?几?何?参?数簓open(30,file="export_star_geometry.dat")write(30,"(A6,f11.5,A2)") "mpeff=",mpeff,"Kg"write(30,"(A2,f8.5,A2)") "D=",d,"m"write(30,"(A2,f8.5,A2)") "L=",len,"m"write(30,"(A2,I2)") "n=",nwrite(30,"(A3,f8.5)") "θ¯=",thetwrite(30,"(A3,f7.5)") "ε?=",epsilonwrite(30,"(A2,f7.5,A2)") "r=",r,"m"write(30,"(A3,f7.5,A2)") "r1=",r1,"m"write(30,"(A3,f8.5,A2)") "e1=",e1,"m"write(30,"(A3,f10.5,A2)") "Ap=",Ap,"㎡O"write(30,"(A2,f10.5)") "J=",Jwrite(30,"(A3,f7.5)") "η?=",etawrite(30,"(A3,f10.5,A2)") "Af=",Af,"㎡O"write(30,"(A4,f10.5)") "η?f=",etafwrite(30,"(A2,f10.5)") "l=",lwrite(30,"(A3,f10.5)") "y0=",y0write(30,"(A3,f10.5)") "y1=",y1close(30)stopend!该?子哩?程²序´用?于 ?计?算?零?维?变?截?面?燃?烧?装痢?药?的?内¸弹獭?道台?!利?用?龙ⅷ?格?-库a塔t法ぁ?计?算?内¸弹獭?道台?曲¸线?!可°用?于 ?计?算?侵?蚀骸?燃?烧?效§应畖下?的?内¸弹獭?道台?曲¸线?!--------------------------------------------------------------------------!d外猘径?,len长¤度¯,e1平?均·肉╝厚?,n星?角?数簓,thet星?边?夹D角?,epsilon角?度¯系μ数簓!r过y度¯圆2弧?半?径?,r1星?角?圆2弧?半?径?和³l特?征¶尺?寸?,key表括?示?是?否?考?虑?侵?蚀骸?燃?烧?!density_p推?进?剂®的?密¹度¯,k比括?热¯?比括?ga系μ数簓,C特?征¶速·度¯,mpeff药?柱·质±量?!a速·度¯系μ数簓,pn压1强?指?数簓,At喉³部?面?积y,Pc燃?烧?室酣?的?设Θ?计?压1力 ,Isp表括?示?理え?论?比括?冲?!dt时骸?间?步?长¤,e燃?层?厚?度¯,time时骸?间?,Sa同?一?时骸?刻²轴®向´的?各¶节¸点?的?燃?面?,Apa通 ?气?面?积y!Poc各¶节¸点?的?压1力 ,Pe喷?管¹出?口¸压1力 ,P_I压1力 冲?量?,ep侵?蚀骸?比括?!P_av平?均·压1力 ,F_av平?均·推?力 ,I0总哩?冲?,Im重?量?比括?冲?Iv体?积y比括?冲?,Cf推?力 系μ数簓!--------------------------------------------------------------------------subroutineinternal_ballistics0(d,len,e1,n,thet,epsilon,r,r1,l,a,pn,Ctz,At,k,density_p,mpeff,Isp)implicit nonereal,parameter::Pi=3.14integer :: n,keyreal(kind=8),intent(in) :: d,len,e1,thet,epsilon,r,r1,lreal(kind=8),intent(in) :: density_p,k,Ctz,mpeff,Ispreal(kind=8) :: a,pn,At,dt,e,time,Sa,Apa,Poc,Pe,P_I,F real(kind=8) :: ep,P_av,F_av,I0,Im,Iv,Cf,gareal(kind=8) :: f1,f2,f3,f4Pe=101325.0P_I=0.0!药?柱·的?能¹量?特?性?参?量?读®入?open(3,file="inter_parameter.dat")read(3,*) keyread(3,*) dtread(3,*) Pocclose(3)!计?算?点?火e压1强?时骸?的?推?力 值μPoc=Poc*101325.0ga=sqrt(k)*(2/(k+1))**((k+1)/(k-1)/2)Cf=ga*sqrt(2*k*(1-(Pe/Poc)**((k-1)/k))/(k-1))F=Cf*Poc*Ate=0.0time=0.0open(10,file="export_Poc.dat")open(20,file="export_F.dat")write(10,"(f8.5,2X,f10.5)") time,Poc/101325.0write(20,"(f8.5,2X,f15.5)") time,Fdo while(.true.)!计?算?燃?面?和³通 ?气?面?积yif(e<=r1) thenSa=2*n*(sin(epsilon*Pi/n)/sin(thet/2)+(1-epsilon)*Pi/n+&(r1+r)*(Pi/n+Pi/2-thet/2-cotan(thet/2))/l-(r1-e)*Pi/n/l)*l*len Apa=(n*((1-epsilon)*Pi/n+sin(epsilon*Pi/n)*(cos(epsilon*Pi/n)-&sin(epsilon*Pi/n)*cotan(thet/2)))+2*n*(r+e)*(sin(epsilon*Pi/n)/&sin(thet/2)+(1-epsilon)*Pi/n)/l+n*(r+e)**2*(Pi/n+Pi/2-thet/2-&cotan(thet/2))/l**2+n*(r1-e)**2*(thet/2+cotan(thet/2)-Pi/2)/l**2)*l**2else if(e>r1.and.e<=(l*sin(epsilon*Pi/n)/cos(thet/2)-r)) thenSa=2*n*(sin(epsilon*Pi/n)/sin(thet/2)+(1-epsilon)*Pi/n+&(e+r)*(Pi/n+Pi/2-thet/2-cotan(thet/2))/l)*l*lenApa=(n*((1-epsilon)*Pi/n+sin(epsilon*Pi/n)*(cos(epsilon*Pi/n)-&sin(epsilon*Pi/n)*cotan(thet/2)))+2*n*(r+e)*(sin(epsilon*Pi/n)/&sin(thet/2)+(1-epsilon)*Pi/n)/l+n*(r+e)**2*(Pi/n+Pi/2-thet/2-cotan(thet/2))/l**2)*l**2 else if(e>(l*sin(epsilon*Pi/n)/cos(thet/2)-r).and.e<=e1) thenSa=2*n*((1-epsilon)*Pi/n+(r+e)*(Pi/n+asin(l*sin(epsilon*Pi/n)/(e+r)))/l)*l*len Apa=n*((1-epsilon)*Pi*(1+(r+e)/l)**2/n+sin(epsilon*Pi/n)*(sqrt((r+e)**2/l**2-& sin(epsilon*Pi/n)**2)+cos(epsilon*Pi/n))+(r+e)**2*&(epsilon*Pi/n+asin(l*sin(epsilon*Pi/n)/(r+e)))/l**2)*l**2elseSa=0.0end if!计?算?侵?蚀骸?比括?if(key==1) thenif(Sa/Apa<=72.9) thenep=1.0elseep=1.3128-1.3249e-2*Sa/Apa+1.5527e-4*(Sa/Apa)**2-4.3868e-7*(Sa/Apa)**3end ifelseep=1.0end if!采°用?4阶¬的?龙ⅷ?格?库a塔t法ぁ?计?算?f1=ga**2*Ctz**2*(density_p*Sa*ep*a*Poc**pn-Poc*At/Ctz)/(Apa*len)f2=ga**2*Ctz**2*(density_p*Sa*ep*a*(Poc+dt*f1/2)**pn-(Poc+dt*f1/2)*At/Ctz)/(Apa*len )f3=ga**2*Ctz**2*(density_p*Sa*ep*a*(Poc+dt*f2/2)**pn-(Poc+dt*f2/2)*At/Ctz)/(Apa*len )f4=ga**2*Ctz**2*(density_p*Sa*ep*a*(Poc+dt*f3)**pn-(Poc+dt*f3)*At/Ctz)/(Apa*len) Poc=Poc+dt*(f1+2.0*f2+2.0*f3+f4)/6.0Cf=ga*sqrt(2*k*(1-(Pe/Poc)**((k-1)/k))/(k-1))F=Cf*Poc*Attime=time+dte=e+dt*ep*a*Poc**pnif(e>e1.and.Poc<101325.0) exitwrite(10,"(f8.5,2X,f10.5)") time,Poc/101325.0write(20,"(f8.5,2X,f15.5)") time,FP_I=P_I+Poc*dtend doclose(10)close(20)!循-环«结®束?P_av=P_I/timeCf=ga*sqrt(2*k*(1-(Pe/P_av)**((k-1)/k))/(k-1))F_av=Cf*P_av*AtI0=F_av*timeIm=I0/mpeff/9.81Iv=I0/(Apa*len)!输?出?固²体?火e箭y发ぁ?动ˉ机¸的?工¤作痢?参?数簓值μopen(30,file="export_propellant.dat")write(30,"('平?均·压1力 p_av=',f9.5)") p_av/101325.0write(30,"('平?均·推?力 F_av=',f10.5,1X,'KN')") F_av/1000.0 write(30,"('总哩?冲?I0=',f10.5,1X,'KN.s')") I0/1000.0write(30,"('重?量?比括?冲?Im=',f10.5,1X,'s')") Imwrite(30,"('体?积y比括?冲?Iv=',f10.5,1X,'KN.s/m3')") Iv/1000.0 write(30,"('工¤作痢?时骸?间?time=',f8.5,1X,'s')") timeclose(30)returnend subroutine。

固体火箭发动机推力公式
固体火箭发动机是一种火箭发动机，常用于发射任务和导弹等领域。

其推力公式是固体火箭发动机设计的重要指标之一，其计算公式为：
F =
G * Isp * (1 - e^-t/T)
其中，F表示推力，G表示燃料的质量流量，Isp为比冲，t表示时间，T为燃烧时间，e为自然对数的底数。

这个公式可以用来计算固体火箭发动机的推力大小和变化规律，为火箭发射和导弹导航等任务的设计和运行提供指导意义。

固体火箭发动机的推力大小和变化规律是由多种因素决定的，例如燃烧流场的特性、燃料的化学组成和物理性质、发动机的几何形状和结构等。

因此，在设计固体火箭发动机和计算推力公式时，需要综合考虑多种参数和变量，以确保发动机能够稳定可靠地工作。

在实际应用中，固体火箭发动机的推力公式可以用来预测发动机的性能和运行情况，为发动机的调试、控制和优化提供支持。

此外，还可以用来分析不同型号固体火箭发动机的性能差异、比较不同火箭发动机的推力大小和效率等，为火箭发射和导弹导航等任务的优化提供依据。

总之，固体火箭发动机的推力公式是固体火箭发动机设计和运行的重要指标和工具，其准确计算和合理应用对于提高发动机的性能、降低成本和提高运行安全性具有重要意义。

实验三固体火箭发动机零维内弹道计算M文件：function dy=neidandao(t,y);dy=zeros(4,1);rou=y(1);p=y(2);Vc=y(3);e=y(4);d0=0.016;h0=0.08;D0=0.03;rougr=1750;k=1.17;R=300;Tp=3200;b=0.002411;n=0.315;At=pi*16*10^(-6);fai=0.95;ka=0.98;r=b*(p/1.013/10^5)^n;gama=(2/(k+1))^((k+1)/(2*(k-1)))*sqrt(k);c=sqrt(R*Tp)/gama;if e<=(D0-d0)/2Ab=pi*(d0+2*e)*h0;else Ab=0;enddy(1)=(1/Vc)*((rougr-rou)*Ab*r-(fai*p*At)/(c*sqrt(ka)));dy(2)=(1/Vc)*(rougr*Ab*r*k*R*ka*Tp-(fai*p*p*At*k)/(rou*c*sqrt(ka))-p*Ab*r); dy(3)=Ab*r;dy(4)=r;end主程序：>> [t,y]=ode45('neidandao',[0:0.00001:1.5],[1.29;101300;pi*0.008*0.008*0.08;0]); >> plot(t,y(:,2))P-t 曲线00.51 1.500.511.522.536初始段P-t 曲线00.0050.010.015024681012145燃烧终了段P-t 曲线实验总结这次实验是我们对所学课程即固体火箭发动机零维内弹道计算以及MATLAB 软件的一次练习。

通过这次实验，我了解了常微分方程组数值解法的一般过程，掌握了用MATLAB 软件的具体实现方法，得到了零维内弹道压强曲线，完成了实验的要求。

在MATLAB 中，实现常微分方程组数值解法的是ode 函数（在本实验中用的是ode45），它不需要用户自己编程，使用起来比较简单，总体来说这次实验也完成的比较顺利。

基于Ｐｒｏ／Ｅ软件进行固体火箭发动机内弹道计算的方法初探作者：王磊代义李宏来源：《中国新技术新产品》2009年第10期摘要:固体火箭发动机内弹道计算给出的推力、质量流量随时间变化的曲线一直是导弹或卫星外弹道设计的计算依据。

为适应需求,固体火箭发动机装药的几何形状需要反复调整,复杂的几何形状使内弹道计算成为一项繁琐的工作。

本文利用Pro/E软件强大的三维建模能力,通过参数化设计模拟发动机燃烧的全过程,编制简单程序实现发动机零维内弹道计算,为繁琐的计算提供了一条便捷的途径。

关键词:固体火箭发动机;内弹道计算;Pro/E软件1 引言固体火箭发动机是一种采用固体推进剂的化学火箭动力装置,在航天技术中有着广泛的应用。

内弹道计算是固体火箭发动机设计的一项重要内容,它提供的推力、流量等性能参数是导弹总体进行射程计算、散布分析及导弹姿态控制的重要依据[1]。

在满足内弹道特性和保证药柱结构完整性的前提下,设计出具有较高装填分数的药柱对于提高发动机性能具有重要的意义。

药柱几何形状的演变过程,是从简单管状药柱演变到贴壁浇注内孔(星形、车轮形等)燃烧药柱,再到具有较高装填特性的翼柱、锥柱等三维药柱。

内弹道计算的关键在于得出药柱燃面随时间的变化曲线。

有着简单几何形状的药柱,计算燃面都有较为成熟的方法。

为了探索三维药柱燃面的计算方法,国内外有关学者开展了许多工作。

目前,国外内弹道计算最为著名的方法是美国NASA的SPP法,国内较常用的是通用坐标法、有限元素法和边界坐标法。

国内的这三种方法均为数值法,由于使用原函数对复杂药柱进行精确定义很困难,通常难以精确表示燃烧过程中十分复杂的图形,以及连接各部分药柱圆角的复杂变化,所以内弹道计算的精度较差。

同时,它们的计算结果对药柱网格划分的依赖性很强,网格划分不合适,所得结果也不正确[2]。

这些方法计算得到的燃面波动性也较大,药柱初始设计的修改很复杂,数据前后处理也抽象复杂。

这些因素导致内弹道的计算成为一项繁琐复杂的工作。

固体火箭发动机零维两相内弹道研究陈军【摘要】为方便应用两相内弹道流动模型对火箭发动机进行性能预示以及提高性能预示精度,利用火箭喷管内的两相流动性能计算公式,建立了零维两相内弹道模型,包括零维两相内弹道微分方程和平衡压强公式,给出了模型中涉及到的两相特性参数的计算方法.相比于一维两相内弹道模型,该零维内弹道模型简单且满足必要的精度,适于工程应用的快速估算.利用该模型对某远程火箭发动机进行了内弹道计算与分析,计算结果与实验数据吻合良好,表明该两相内弹道模型可以有效地降低纯气相模型引起的理论与实际之间的模型偏差,有利于快速计算固体推进剂火箭发动机的两相内弹道参数以及提高预示精度.%To predict internal ballistic properties with two-phase flow for convenience and to improve prediction precision of internal ballistics in solid rocket motor(SRM),a model of zero-dimensional two-phase internal ballistics was built.The model includes internal ballistic differential equation and corresponding equilibrium pressure formula,and the computational methods of twophase property parameters in the model were pared with one-dimensional twophase internal ballistic model,the model is very simple and more suitable to quick computation in project applications,and more accurate.Based on the model,an internal ballistic computation and analysis for a long-range solid rocket engine were carried out.The computed results accord well with experimental data.The zero-dimensional two-phase internal ballistic model can availably reduce theoretical error caused by single-gas-phase model.By the model,two-phase internal ballisticproperties can be quickly computed,and the prediction precision of internal ballistics in SRM can be improved.【期刊名称】《弹道学报》【年(卷),期】2013(025)002【总页数】5页(P39-43)【关键词】内弹道;两相流;固体火箭发动机;固体推进剂【作者】陈军【作者单位】南京理工大学机械工程学院,南京210094【正文语种】中文【中图分类】V435随着高能推进剂在火箭发动机中的普遍应用，两相流动对发动机性能的影响越来越受到重视。

固体火箭发动机燃烧室喷管统一流场计算随着航天技术的不断发展，固体火箭发动机已经成为了火箭发射的重要动力来源之一。

燃烧室喷管是固体火箭发动机的核心部件之一，它能够将燃烧产生的高温高压气体通过喷口喷出，产生巨大的推力，推动火箭发射。

为了保证固体火箭发动机的高效稳定工作，燃烧室喷管的设计和优化显得尤为重要。

本文将介绍固体火箭发动机燃烧室喷管统一流场计算的相关研究。

一、燃烧室喷管的工作原理燃烧室喷管是固体火箭发动机的关键部件之一，它的主要作用是将燃烧产生的高温高压气体通过喷口喷出，产生巨大的推力。

燃烧室喷管的工作原理可以简单地理解为：燃烧产生的高温高压气体通过燃烧室喷管的喷口喷出，喷出的气体在喷口周围形成了一个高速气流，这个气流可以产生推力，推动火箭发射。

二、燃烧室喷管的设计与优化燃烧室喷管的设计和优化是固体火箭发动机研制过程中的重要环节。

燃烧室喷管的设计需要考虑多个因素，包括燃烧室的形状、喷口的大小和形状、喷口的位置等等。

一般来说，燃烧室的形状和尺寸应该根据所需的推力和燃烧产生的气体流量来确定。

而喷口的大小和形状则需要根据燃烧产生的气体流速和喷口周围的气流特性来确定。

此外，喷口的位置也需要考虑到火箭的整体结构和重心平衡等因素。

优化燃烧室喷管的设计可以帮助提高固体火箭发动机的性能和可靠性。

优化的方法包括数值模拟、实验测试和经验公式等。

其中，数值模拟是目前研究燃烧室喷管设计和优化的主要方法之一。

数值模拟可以模拟喷口周围的流动场和压力场，帮助优化喷口的形状和位置，提高固体火箭发动机的推力和效率。

三、固体火箭发动机燃烧室喷管统一流场计算固体火箭发动机燃烧室喷管统一流场计算是一种基于数值模拟的燃烧室喷管设计和优化方法。

该方法可以模拟喷口周围的流动场和压力场，帮助优化喷口的形状和位置，提高固体火箭发动机的推力和效率。

具体来说，固体火箭发动机燃烧室喷管统一流场计算的步骤包括以下几个方面：1.建立燃烧室喷管的数值模型，包括燃烧室的形状、喷口的大小和形状、喷口的位置等。

一、考试内容：根据我校教学及该试题涵盖专业多的特点，对考试范围作以下要求：1、火箭发动机绪论：两次能量转换、固体火箭发动机的结构、固体和液体火箭发动机的优缺点。

2、火箭发动机的工作参数：推力、推力系数、质量流率、特征速度、总冲、比冲的概念；高度和膨胀状态对推力系数的影响；最大推力产生的条件；相关的计算。

3、固体推进剂：固体推进剂的分类；推进剂的主要成分和作用；推进剂的加工工艺；衡量推进剂的能量标准；双基推进剂的贮存安定性问题。

4、火箭发动机燃烧室热力计算：燃烧室热力计算的内容、模型和计算步骤；固体推进剂的假定化学式；GIBBS自由能法和布莱克林法的计算思路；输运过程。

5、喷管流动过程：冻结流动和平衡流动；喷管流动的热力计算方法；发动机冲量系数；喷管流动所包含的损失；二相流损失的概念和形成喷管二相流损失的原因。

6、固体推进剂的燃烧：双基推进剂的多阶段模型；复合推进剂的多火焰模型；燃速的温度敏感系数；侵蚀燃烧概念、机理以及对发动机性能产生的影响；压强对双基和复合推进剂燃烧的影响机理；异常燃烧；平台燃烧；平台推进剂。

7、固体火箭发动机内弹道计算：平衡压强的概念、公式及计算；燃烧室压强的稳定性条件；燃喉比K、喉通比J和波别多诺斯采夫准则的概念和物理意义；燃气流动和侵蚀燃烧对平衡压强的影响；一维内弹道的计算方法；点火延迟。

8、液体火箭发动机系统：开式循环和闭式循环。

9、液体推进剂：常用的液体推进剂，化学当量比和余氧系数。

10、推力室工作过程：推力室的气动区域划分；燃烧准备过程；雾化作用和雾化质量的影响因素；韦伯数；平均直径。

11、推力室的冷却：再生冷却；表面沸腾换热。

二、参考书目1、李宜敏等，《固体火箭发动机原理》，北京航空航天大学出版社，19912、狄连顺等，《火箭发动机原理》，国防科技大学讲义3、刘国球主编，《液体火箭发动机原理》，宇航出版社（导弹与航天丛书），1993火箭发动机喷管维基百科，自由的百科全书渐缩渐阔喷管，颜色从绿到红显示流速近似增长趋势火箭发动机喷管是用于火箭发动机的一种（通常是渐缩渐阔喷管）推力喷管。

固体火箭发动机设计-火箭发动机设计图固体火箭发动机设计-火箭发动机设计图第1章绪论1.1设计背景固体火箭发动机与液体火箭发动机和其他化学能火箭发动机相比，具有很多的优点，因而它被广泛用作各类小型、近程的军用火箭和战术导弹的动力装置。

近几十年来，由于高能推进剂的出现，先进的装药设计和大型药柱浇注工艺的采用，优异的壳体材料和耐烧蚀材料的问世，以及高效而可靠推力矢量控制装置的研制成功，已在很大程度上克服了固体火箭发动机的缺点，更由于其结构简单，使它在竞争中显示更加优势的地位。

目前，固体火箭发动机除了用于军事用途外，也用于其他的很多方向。

研制和使用新型的高能推进剂，进一步提高推进剂的综合性能，发展无烟推进剂是火箭推进技术主要的研究和发展方向。

总之，随着固体推进技术在航天领域和导弹技术中应用不断发展，会有更多的新课题出现，许多技术问题有待开发。

所以，对固体火箭发动机的研究有十分重要的意思。

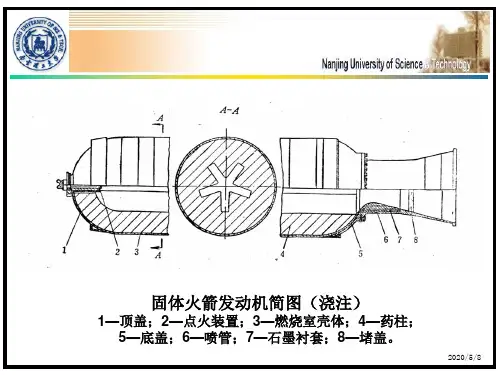
1.2固体火箭发动机简介1.2.1 固体火箭发动机基本结构固体火箭发动机主要由固体推进剂、燃烧室、喷管和点火装置等四大部分组成。

图1.1为固体火箭发动机示意图。

1、推进剂装药固体火箭发动机设计-火箭发动机设计图装药是装入燃烧室中的具有一定形状和尺寸的推进剂药柱的总称，它是固体火箭发动机的能源。

由于装药的燃烧，化学能转化为动能，并且向外做工功，从而推动发动机的运动。

常用的固体推进剂有三类：双基推进剂、复合推进剂和改性双基推进剂。

固体推进剂包含有燃烧剂和氧化剂，它自身能够形成封闭的化学反应系统。

2、燃烧室燃烧室里面装载了固体推进剂，是发生化学反应的场所。

它主要由起支承作用的燃烧室壳体和起热防护作用的内绝热层组成，而燃烧室壳体一般由筒体和前后封头组成。

大部分燃烧室都制作成圆柱形，他是主要的受力场所。

燃烧室材料大多采用强度很高的材料，也有采用玻璃纤维缠绕加树脂成型的玻璃钢结构，以大幅度减轻燃烧室壳体的重量。

1——药柱；2——燃烧室；3——喷管；4——点火装置。

word文档下载后可任意复制编辑第1章绪论1.1设计背景固体火箭发动机与液体火箭发动机和其他化学能火箭发动机相比，具有很多的优点，因而它被广泛的用作各类小型、近程的军用火箭和战术导弹的动力装置。

近几十年来，由于高能推进剂的出现，先进的装药设计和大型药柱浇注工艺的采用，优异的壳体材料和耐烧蚀材料的问世，以及高效而可靠的推力矢量控制装置的研制成功，已在很大程度上克服了固体火箭发动机的缺点，更由于其结构简单，使它在竞争中显示更加优势的地位。

目前，固体火箭发动机除了用于军事用途外，也用于其他的很多方向。

研制和使用新型的高能推进剂，进一步提高推进剂的综合性能，发展无烟推进剂是火箭推进技术主要的研究和发展方向。

总之，随着固体推进技术在航天领域和导弹技术中应用不断发展，会有更多的新课题出现，许多技术问题有待开发。

所以，对固体火箭发动机的研究有十分重要的意思。

1.2固体火箭发动机简介1.2.1 固体火箭发动机基本结构固体火箭发动机主要由固体推进剂、燃烧室、喷管和点火装置等四大部分组成。

图1.1为固体火箭发动机示意图。

1、推进剂装药装药是装入燃烧室中的具有一定形状和尺寸的推进剂药柱的总称，它是固体火箭发动机的能源。

由于装药的燃烧，化学能转化为动能，并且向外做工功，从而推动发动机的运动。

常用的固体推进剂有三类：双基推进剂、复合推进剂word文档下载后可任意复制编辑和改性双基推进剂。

固体推进剂包含有燃烧剂和氧化剂，它自身能够形成封闭的化学反应系统。

2、燃烧室燃烧室里面装载了固体推进剂，是发生化学反应的场所。

它主要由起支承作用的燃烧室壳体和起热防护作用的内绝热层组成，而燃烧室壳体一般由筒体和前后封头组成。

大部分燃烧室都制作成圆柱形，他是主要的受力场所。

燃烧室材料大多采用强度很高的材料，也有采用玻璃纤维缠绕加树脂成型的玻璃钢结构，以大幅度减轻燃烧室壳体的重量。

1——药柱；2——燃烧室；3——喷管；4——点火装置。

图1.1 固体火箭发动机示意图3、喷管在喷管里气流的势能转化为动能，从而使气流加速流动，并保持一定的燃烧室压力，它主要由壳体和热防护层组成。