华师大版九年级(上) 中考题单元试卷:第25章 解直角三角形(06)
- 格式:pdf
- 大小:635.64 KB
- 文档页数:13

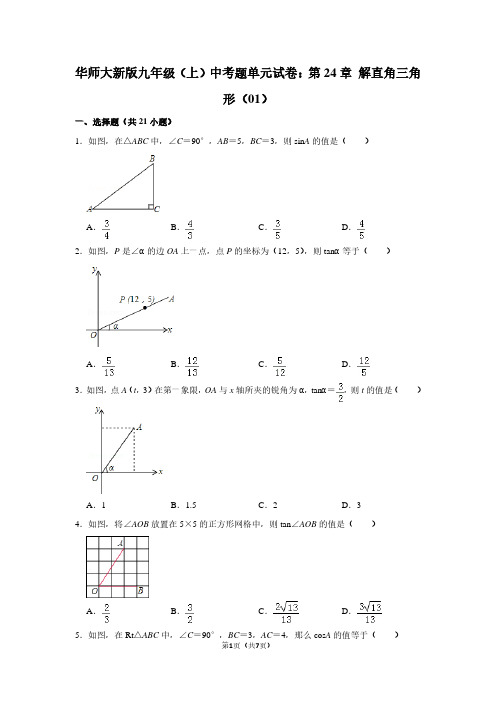


华师大新版九年级(上)中考题同步试卷:24.4 解直角三角形(06)一、选择题(共2小题)1.湖南路大桥于今年5月1日竣工,为徒骇河景区增添了一道亮丽的风景线.某校数学兴趣小组用测量仪器测量该大桥的桥塔高度,在距桥塔AB底部50米的C处,测得桥塔顶部A的仰角为41.5°(如图).已知测量仪器CD的高度为1米,则桥塔AB的高度约为()(参考数据:sin41.5°≈0.663,cos41.5°≈0.749,tan41.5°≈0.885)A.34米B.38米C.45米D.50米2.如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A 的仰角为30°,再向电视塔方向前进100米达到F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB(单位:米)为()A.50B.51C.50+1D.101二、填空题(共6小题)3.如图,小华站在河岸上的G点,看见河里有一小船沿垂直于岸边的方向划过来.此时,测得小船C的俯角是∠FDC=30°,若小华的眼睛与地面的距离是1.6米,BG=0.7米,BG平行于AC所在的直线,迎水坡i=4:3,坡长AB=8米,点A、B、C、D、F、G在同一平面内,则此时小船C到岸边的距离CA的长为米.(结果保留根号)4.某校数学兴趣小组要测量西山植物园蒲宁之珠的高度.如图,他们在点A处测得蒲宁之珠最高点C的仰角为45°,再往蒲宁之珠方向前进至点B处测得最高点C的仰角为56°,AB=62m,根据这个兴趣小组测得的数据,则蒲宁之珠的高度CD约为m.(sin56°≈0.83,tan56°≈1.49,结果保留整数)5.如图,某建筑物BC上有一旗杆AB,从与BC相距38m的D处观测旗杆顶部A的仰角(结果精确到0.1m,为50°,观测旗杆底部B的仰角为45°,则旗杆的高度约为m.参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)6.如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,那么山高AD为米(结果保留整数,测角仪忽略不计,≈1.414,,1.732)7.如图,从一个建筑物的A处测得对面楼BC的顶部B的仰角为32°,底部C的俯角为45°,观测点与楼的水平距离AD为31m,则楼BC的高度约为m(结果取整数).(参考数据:sin32°≈0.5,cos32°≈0.8,tan32°≈0.6)8.4月26日,2015黄河口(东营)国际马拉松比赛拉开帷幕,中央电视台体育频道用直升机航拍技术全程直播.如图,在直升机的镜头下,观测马拉松景观大道A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则AB两点的距离是米.三、解答题(共22小题)9.如图所示,体育场内一看台与地面所成夹角为30°,看台最低点A到最高点B的距离为10,A,B两点正前方有垂直于地面的旗杆DE.在A,B两点处用仪器测量旗杆顶端E的仰角分别为60°和15°(仰角即视线与水平线的夹角)(1)求AE的长;(2)已知旗杆上有一面旗在离地1米的F点处,这面旗以0.5米/秒的速度匀速上升,求这面旗到达旗杆顶端需要多少秒?10.“东方之星”客船失事之后,本着“关爱生命,救人第一”的宗旨.搜救部门紧急派遣直升机到失事地点进行搜救,搜救过程中,假设直升机飞到A处时,发现前方江面上B 处有一漂浮物,从A测得B处的俯角为30°,已知该直升机一直保持在距江面100米高度飞行搜索,飞行速度为10米每秒,求该直升机沿直线方向朝漂浮物飞行多少秒可到达漂浮物的正上方?(结果精确到0.1,≈1.73)11.张老师利用休息时间组织学生测量山坡上一棵大树CD的高度,如图,山坡与水平面成30°角(即∠MAN=30°),在山坡底部A处测得大树顶端点C的仰角为45°,沿坡面前进20米,到达B处,又测得树顶端点C的仰角为60°(图中各点均在同一平面内),求这棵大树CD的高度(结果精确到0.1米,参考数据:≈1.732)12.如图,建筑物AB后有一座假山,其坡度为i=1:,山坡上E点处有一凉亭,测得假山坡脚C与建筑物水平距离BC=25米,与凉亭距离CE=20米,某人从建筑物顶端测得E点的俯角为45°,求建筑物AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)13.热气球的探测器显示,从热气球底部A处看一栋高楼顶部的俯角为30°,看这栋楼底部的俯角为60°,热气球A处于地面距离为420米,求这栋楼的高度.14.为了弘扬“社会主义核心价值观”,市政府在广场树立公益广告牌,如图所示,为固定广告牌,在两侧加固钢缆,已知钢缆底端D距广告牌立柱距离CD为3米,从D点测得广告牌顶端A点和底端B点的仰角分别是60°和45°.(1)求公益广告牌的高度AB;(2)求加固钢缆AD和BD的长.(注意:本题中的计算过程和结果均保留根号)15.如图,某中学九年级数学兴趣小组测量校内旗杆AB的高度,在C点测得旗杆顶端A 的仰角∠BCA=30°,向前走了20米到达D点,在D点测得旗杆顶端A的仰角∠BDA =60°,求旗杆AB的高度.(结果保留根号)16.如图,线段AB,CD表示甲、乙两幢居民楼的高,两楼间的距离BD是60米.某人站在A处测得C点的俯角为37°,D点的俯角为48°(人的身高忽略不计),求乙楼的高度CD.(参考数据:sin37°≈,tan37°≈,sin48°≈,tan48°≈)17.如图,某建筑物BC顶部有一旗杆AB,且点A,B,C在同一条直线上,小红在D处观测旗杆顶部A的仰角为47°,观测旗杆底部B的仰角为42°已知点D到地面的距离DE 为1.56m,EC=21m,求旗杆AB的高度和建筑物BC的高度(结果保留小数后一位).参考数据:tan47°≈1.07,tan42°≈0.90.18.一数学兴趣小组为了测量河对岸树AB的高,在河岸边选择一点C,从C处测得树梢A 的仰角为45°,沿BC方向后退10米到点D,再次测得A的仰角为30°,求树高.(结果精确到0.1米,参考数据:≈1.414,≈1.732)19.如图,两幢建筑物AB和CD,AB⊥BD,CD⊥BD,AB=15m,CD=20m,AB和CD 之间有一景观池,小南在A点测得池中喷泉处E点的俯角为42°,在C点测得E点的俯角为45°(点B、E、D在同一直线上),求两幢建筑物之间的距离BD(结果精确到0.1m).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)20.小敏同学测量一建筑物CD的高度,她站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走30m,到达点F处测得楼顶C的仰角为45°(BFD在同一直线上).已知小敏的眼睛与地面距离为1.5m,求这栋建筑物CD的高度(参考数据:≈1.732,≈1.414.结果保留整数)21.如图是放在水平地面上的一把椅子的侧面图,椅子高为AC,椅面宽为BE,椅脚高为ED,且AC⊥BE,AC⊥CD,AC∥ED.从点A测得点D、E的俯角分别为64°和53°.已知ED=35cm,求椅子高AC约为多少?(参考数据:tan53°≈,sin53°≈,tan64°≈2,sin64°≈)22.如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°,若坡角∠F AE=30°,求大树的高度(结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,≈1.73)23.如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果精确到0.1米)24.如图,某数学兴趣小组在活动课上测量学校旗杆的高度.已知小亮站着测量,眼睛与地面的距离(AB)是1.7米,看旗杆顶部E的仰角为30°;小敏蹲着测量,眼睛与地面的距离(CD)是0.7米,看旗杆顶部E的仰角为45°.两人相距5米且位于旗杆同侧(点B、D、F在同一直线上).(1)求小敏到旗杆的距离DF.(结果保留根号)(2)求旗杆EF的高度.(结果保留整数,参考数据:≈1.4,≈1.7)25.小强从自己家的阳台上,看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,小强家与这栋楼的水平距离为42m,这栋楼有多高?26.如图,热气球的探测器显示,从热气球A处看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为65°,热气球与高楼的水平距离AD为120m.求这栋高楼的高度.(结果用含非特殊角的三角函数及根式表示即可)27.某水库大坝的横截面是如图所示的四边形ABCD,其中AB∥CD,大坝顶上有一瞭望台PC,PC正前方有两艘渔船M,N.观察员在瞭望台顶端P处观测到渔船M的俯角α为31°,渔船N的俯角β为45°.已知MN所在直线与PC所在直线垂直,垂足为E,且PE长为30米.(1)求两渔船M,N之间的距离(结果精确到1米);(2)已知坝高24米,坝长100米,背水坡AD的坡度i=1:0.25,为提高大坝防洪能力,请施工队将大坝的背水坡通过填筑土石方进行加固,坝底BA加宽后变为BH,加固后背水坡DH的坡度i=1:1.75,施工队施工10天后,为尽快完成加固任务,施工队增加了机械设备,工作效率提高到原来的2倍,结果比原计划提前20天完成加固任务,施工队原计划平均每天填筑土石方多少立方米?(参考数据:tan31°≈0.60,sin31°≈0.52)28.如图,观测点A、旗杆DE的底端D、某楼房CB的底端C三点在一条直线上,从点A 处测得楼顶端B的仰角为22°,此时点E恰好在AB上,从点D处测得楼顶端B的仰角为38.5°.已知旗杆DE的高度为12米,试求楼房CB的高度.(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin38.5°≈0.62,cos38.5°≈0.78,tan38.5°≈0.80)29.小华为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.(以下计算结果精确到0.1m)(1)求小华此时与地面的垂直距离CD的值;(2)小华的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,求楼房AB的高度.30.如图所示,小明家小区空地上有两棵笔直的树CD、EF.一天,他在A处测得树顶D 的仰角∠DAC=30°,在B处测得树顶F的仰角∠FBE=45°,线段BF恰好经过树顶D.已知A、B两处的距离为2米,两棵树之间的距离CE=3米,A、B、C、E四点在一条直线上,求树EF的高度.(≈1.7,≈1.4,结果保留一位小数)华师大新版九年级(上)中考题同步试卷:24.4 解直角三角形(06)参考答案一、选择题(共2小题)1.C;2.C;二、填空题(共6小题)3.8﹣5.5;4.189;5.7.2;6.137;7.50;8.200+200;三、解答题(共22小题)9.;10.;11.;12.;13.;14.;15.;16.;17.;18.;19.;20.;21.;22.;23.;24.;25.;26.;27.;28.;29.;30.;第11页(共11页)。
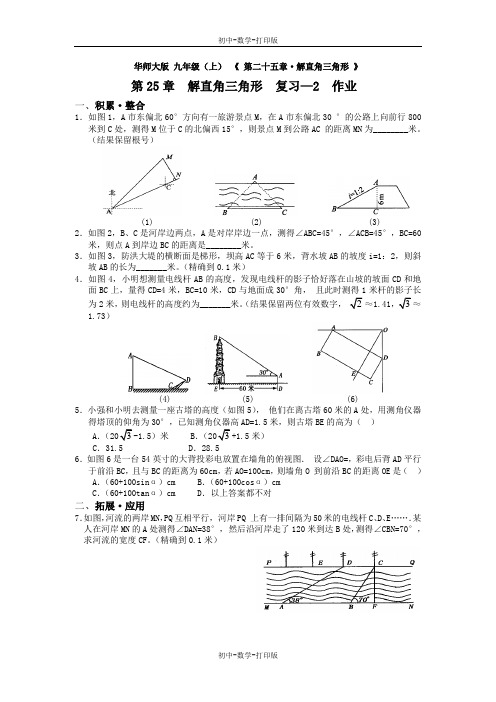
华师大版九年级(上)《第二十五章·解直角三角形》第25章解直角三角形复习—2 作业一、积累·整合1.如图1,A市东偏北60°方向有一旅游景点M,在A市东偏北30•°的公路上向前行800米到C处,测得M位于C的北偏西15°,则景点M到公路AC•的距离MN为________米。
(结果保留根号)(1) (2) (3)2.如图2,B、C是河岸边两点,A是对岸岸边一点,测得∠ABC=45°,∠ACB=45°,BC=60米,则点A到岸边BC的距离是________米。
3.如图3,防洪大堤的横断面是梯形,坝高AC等于6米,背水坡AB的坡度i=1:2,则斜坡AB的长为_______米。
(精确到0.1米)4.如图4,小明想测量电线杆AB的高度,发现电线杆的影子恰好落在山坡的坡面CD和地面BC上,量得CD=4米,BC=10米,CD与地面成30°角,•且此时测得1米杆的影子长为2米,则电线杆的高度约为_______米。
(结果保留两位有效数字,•2≈1.41,3≈1.73)(4) (5) (6)5.小强和小明去测量一座古塔的高度(如图5),•他们在离古塔60米的A处,用测角仪器得塔顶的仰角为30°,已知测角仪器高AD=1.5米,则古塔BE的高为()A.(203-1.5)米 B.(203+1.5米)C.31.5 D.28.56.如图6是一台54英寸的大背投彩电放置在墙角的俯视图.•设∠DAO=,彩电后背AD平行于前沿BC,且与BC的距离为60cm,若AO=100cm,则墙角O•到前沿BC的距离OE是() A.(60+100sinα)cm B.(60+100cosα)cmC.(60+100tanα)cm D.以上答案都不对二、拓展·应用7.如图,河流的两岸MN,PQ互相平行,•河岸PQ•上有一排间隔为50米的电线杆C、D、E…….某人在河岸MN的A处测得∠DAN=38°,•然后沿河岸走了120米到达B处,测得∠CBN=70°,求河流的宽度CF。

解直角三角形测试题一、选择题 1、在 Rt △ ABC 中, / C=90° , a: =1 ,c = 4 ,则sinA 的值是 ( )A .15 1 1 D 、 ■ 15 A 、c —15 4 34 2、在厶ABC 中,乙C =90,如果 tan A -5,那么sin B 的值等于( 125 12 5 12A 、B 、 c 、 D 、 —13 13 12 53、在上一二「中,若 sin2 ,则■■ ■ ?的值为()A. 1B. C. D.2 22AB 等于( ) 4、如图,为了测量河两岸 A 、B 两点的距离, / ACB = ,那么 5、 A. a sin : C. a ta n :r e 2 如果 sin a + sin A.15 6、 于7、 B. a cos : D. a cot : 勺0°=1 那么锐角a B.30 C. AE CF 是锐角△ ABC 的两条高,如果 ) 3: 2 (B ) 2: 3 在厶 ABC 中,/ C = 90O4 5 AE (A ) 如图, 9: 4 (C ) ,/ B = 50 (D ) 4: 9,AB = 10,贝U BC 的长为 A. 10tan50 ° B 、10cos20 C 、 10sin50cos50 B&王英同学从A 地沿北偏西60o 方向走100m 到B 地,再从B 地向正南 方向走200m 到C 地,此时王英同学离 A 地 ( ) (A ) 50.3 m (B ) 100 m (C ) 150m ( D ) 100. 3 m 9、一艘轮船由海平面上 A 地出发向南偏西400的方向行驶40海里到达 B 地,再由B 地向北偏西20o 的方向行驶40海里到达C 地,则A 、C 两 地相距( ) (A ) 30海里 (B ) 40海里 (C ) 50海里 (D ) 60海里10、化简.(ta n30 -1)2 A 、 1 3 二、填空题 11、计算:2si n60 = B 、 C 、」-13则拉线AC 的长是 m.16、如图,一艘轮船向正东方向航行,上午灯塔120海里的M 处,上午11时到达这座灯塔的正南方向的N 处, 内航行的平均速度是 _________ 海里/时。
【九年级】九年级上册第25章解直角三角形测试题(华师大版有答案)第25章解直角三角形检测题(时间:90分钟,满分:100分)一、(每小题3分,共30分)1.计算:a.b.c.d.2.在△, ∠ = 90°,如果,,那么sin的值是()a.b.c.d.3.在△, ∠ = 90,然后是罪()a.b.c.d.4.在△ ABC,如果三边BC、Ca和ab满足BC∶ Ca∶ AB=5∶ 12∶ 13,然后CoSb() a.b.c.d.5.在△, ∠ = 90°,则sin的值为()a.b.c.1d.6.已知于,,则的值为()a.b.c.d.7.如图所示,一个小球沿着斜坡从地面向上移动10。
此时,小球离地面的高度为()a.b.2c.4d.8.如图所示,在钻石中,,,Tan的值∠ 是()a.b.2c.d.9.如果直角三角形的两条右边之和为7,面积为6,则斜边的长度为()a.5b.c.7d.10.如图所示,已知45°<a<90°,则以下公式为真()a.b.c、 d。
二、题(每小题3分,共24分)11.那么__12.若∠是锐角,cos=,则∠=_________.13.小兰想测量南塔的高度她抬头看了看塔顶,测量了30°的仰角,然后向塔的方向移动了50°,测量了60°的仰角,所以塔的高度大约是___________________14.等腰三角形的腰长为2,腰上的高为1,则它的底角等于________.15.如图所示,如果斜面上的高度为RT△ 那就知道了___16.△abc的顶点都在方格纸的格点上,则_.17.数字① 是中国古代著名的“赵双弦图”的示意图,它被四个全等的直角三角形包围。
如果四个直角三角形中边长为6的直角边向外翻倍,得到图中所示的“数学风车”②, 风车的周长是____18.如图是一个艺术窗的一部分,所有的四边形都是正方形,三角形是直角三角形,其中最大正方形的边长为,则正方形a,b的面积和是_________.三、回答问题(共46分)19.(8分)计算下列各题:(1);(2).20.(6分)在数学活动课上,九年级(1)班数学兴趣小组的同学们测量校园内一棵大树的高度,设计的方案及测量数据如下:(1)在树前的平地上选择一个点,测量树顶与该点的仰角为35°;(2)在点和大树之间选择一点(、、在同一直线上),测得由点看大树顶端的仰角恰好为45°;(3)两个测量点之间的距离为4.5请你根据以上数据求出大树的高度.(结果保留3个有效数字)21.(6分)每年的5月15日是“世界残疾人日”。
第25章解直角三角形检测试题时刻:60分钟品级 一、选择题:在每题给出的四个选项中,只有一个是正确的,请将所选选项的字母写在题后的括号中 1.在△ABC 中, AB =5,AC =4,BC=3那么sinA 的值是( )。
A .53B .54C .35D .432.已知α为锐角,且3tan(α+100)=1,那么α的度数为( )。
A .30°B .45°C .20°D .35°3.在正方形网格中,△ABC 的位置如下图,那么tan B ∠的值为( )。
A .1B .3C .32D .33 4.已知Rt △ABC 中,∠C =90︒,tanA=31,且AC=33,则BC 的值为( ).A .43B .83C .4D .35一辆汽车沿倾斜角是α的斜坡行驶500米,那么它上升的高度是()A.500sin α米B.500sin α米C.500cos α米D.500cos α米6.以下说法中,正确的选项是( )+cos300=1.B.若α为锐角,那么2)1(sin -α﹦1﹣sin α.C.关于锐角β,必有sin cos ββ<.D.在Rt △ABC 中,∠C =90︒,那么有tan A 7.如图,是一个中心对称图形,A 为对称中心,假设∠C=90°, ∠B=30°,BC=1,那么BB ′的长为( ). A .4 B .33 C .332 D .3348.以下各式中正确的选项是( )A sin300+cos600=1B sinA=21=300第3题图第7题图30° ACB ′B C ′C cos600=cos(2×300 )=2cos300D tan600+cot450=23 9.当锐角A >300时,cosA 的值是( ) A 小于21 B 大于21 C 小于23 D 大于2310.等腰三角形一腰上的高线为1,且高线与底边的夹角的正切值为1,那么那个等腰三角形的面积为( )。
第25章《解直角三角形》整章测试一.选择题(每小题3分,共24分)1.在Rt △ABC 中, ∠C=90︒,AB=4,AC=1,则cos A 的值是( )(A(B)14(D)42.计算:2)130(tan -︒=( )(A)331-(B)13- (C)133- (D )1-3 3.在ABC ∆中,,A B ∠∠都是锐角,且sinA =21, cosB =23,则ABC ∆的形状( ) (A )直角三角形(B )钝角三角形 (C )锐角三角形 (D )不能确定4.如图,在Rt ABC △中,tan B =,BC =则AC 等于( ) (A )3(B )4(C)(D )65.如图,小颖利用有一个锐角是30°的三角板测量一棵树的高度,已知她与树之间的水平距离BE 为5m ,AB 为1.5m (即小颖的 眼睛距地面的距离),那么这棵树高是( ) (A)32)m (B)(32)m (D)4m 6.因为1sin 302=,1sin 2102=-, 所以sin 210sin(18030)sin30=+=-;因为2sin 45=,sin 225=-, 所以sin 225sin(18045)sin 45=+=-,由此猜想,推理知:一般地当α为锐角时有sin(180)sin αα+=-,由此可知:sin 240=( )(A )12-(B)-(C)-(D)7.如图,客轮在海上以30km/h 的速度由B 向C 航行,在B 处测得 灯塔A 的方位角为北偏东80,测得C 处的方位角为南偏东25,航行1小时后到达C 处,在C 处测得A 的方位角为北偏东20,则C 到A 的距离是( )(A)(B)(C)km (D)km北8.如图,在Rt ABC △中,906cm A AC ∠==,,8cm AB =,把AB 边翻折,使AB 边落在BC 边上,点A 落在点E 处,折痕为BD , 则sin DBE ∠的值为( ) (A)13(B)310二.填空题(每小题3分,共24分) 9.计算sin 60tan 45cos30-的值是 .10. 用“>”或“<”号填空:1sin 50cos 402-0.(可用计算器计算) 11.在Rt ABC △中,90C ∠=,:3:4BC AC =,则cos A = . 12.如图,一架梯子斜靠在墙上,若梯子到墙的距离AC =3米,3cos 4BAC ∠=,则梯子AB 的长度为 米.13.如图,一轮船由南向北航行到O 处时,发现与轮船相距40海里的A 岛在北偏东33方向.已知A 岛周围20海里水域有暗礁, 如果不改变航向,轮船 (填“有”或“没有”)触暗礁 的危险.(可使用科学计算器)14. 如图,在菱形ABCD 中,DE ⊥AB ,垂足为E ,DE=6cm ,3sin 5A =,则菱形ABCD 的面积是__________2cm . 15.根据指令[s,A](s ≥0,0°≤A <360°)机器人在平面上能完成如下动作:先在原地逆时针旋转角度A ,再朝其面对的方向沿直线行走距离s .现在机器人在平面直角坐标系的原点,且面对y 轴的负方向,为使其移动到点(-3,3),应下的指令是 .16. 有古诗“葭生池中”今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问: 水深.葭长各几何?(1丈=10尺)回答:水深 ,葭长 . 三.解答题(本大题共52分)17.(本题845sin 60)4︒-︒+.ABCDEA BC18.(本题10分)某校数学兴趣小组在测量一座池塘边上A B ,两点间的距离时用了以下三种测量方法,如下图所示.图中a b c ,,表示长度,β表示角度.请你求出AB 的长度(用含有a b c β,,,(1)______AB = (2)______AB = (3)______AB =19.(本题10分)小强家有一块三角形菜地,量得两边长分别为40m ,50m ,第三边上的高为30m ,请你帮小强计算这块菜地的面积(结果保留根号).20.(本题12分)海中有一个小岛P ,它的周围18海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A 测得小岛P 在北偏东60°方向上,航行12海里到达B 点,这时测得小岛P 在北偏东45°方向上.如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由.(1)c21.(本题12分)如图,AC 是某市环城路的一段,AE ,BF ,CD 都是南北方向的街道,其与环城路AC 的交叉路口分别是A ,B ,C .经测量花卉世界D 位于点A 的北偏东45°方向.点B 的北偏东30°方向上,AB =2km ,∠DAC=15°. (1)求B ,D 之间的距离; (2)求C ,D 之间的距离.四.附加题(本题20分)22. 现代家居设计的“推拉式”钢窗,运用了轨道滑行技术,纱窗装卸时利用了平行四边形的不稳定性,操作步骤如下:(1)将矩形纱窗转化成平行四边形纱窗后,纱窗上边框嵌入窗框的上轨道槽(如图1). (2)将平行四边形纱窗的下边框对准窗框的下轨道槽(如图2).(3)将平行四边形纱窗还原成矩形纱窗,同时下边框嵌入窗框的下轨道槽(如图3).在装卸纱窗的过程中,如图所示α∠的值不得小于81,否则纱窗受损.现将高96cm 的矩形纱窗恰好安装在上.下槽深分别为0.9cm ,高96cm (上.下槽底间的距离)的窗框上.试求合理安装纱窗时α∠的最大整数值.(下表提供的数据可供使用)ABC 中山路文化路D 和平路45° 15° 30°EF 图1图2图3参考答案一.1~8 BABA ACDD 二.9.0 10. > 11.3512. 4 13.没有 14. 6015.225⎡⎤⎣⎦16. 12尺,13尺三.17.解:=原式2=2=18.解:(1)AB = (2)tan AB a β= (3)ac AB b=. 19.解:分两种情况:(1)当ACB ∠为钝角时, BD 是高,90ADB ∴∠=.在Rt BCD △中,40BC =,30BD =∴CD ===在Rt ABD △中,50AB =,∴40AD ==.40AC AD CD ∴=-=-∴211(4030(600)22ABC S AC BD ==-⨯=-△. (2)当ACB ∠为锐角时, BD 是高,90ADB BDC ∴∠=∠=,在Rt ABD △中,5030AB BD ==,,40AD ∴==.同理CD ===∴(40AC AD CD =+=+,∴211(4030(600)22ABC S AC BD ==+⨯=+△.综上所述:2(600)ABC S =±△.20.解:有触礁危险.理由: 过点P 作PD ⊥AC 于D .设PD 为x ,在Rt △PBD 中,∠PBD=90°-45°=45°. ∴BD =PD =x .在Rt △PAD 中,∵∠PAD =90°-60°=30°,∴x .xAD 330tan =︒= ∵BD ,AB AD +=∴x .x +=123 ∴)13(61312+=-=x .∵,<18)13(6+∴渔船不改变航线继续向东航行,有触礁危险.21. 解:(1)由题意得,∠EA D =45°,∠FBD=30°.∴ ∠EAC=∠EA D +∠DA C =45°+15°=60°. ∵ AE∥BF∥CD,∴ ∠FBC=∠EAC =60°. ∴ ∠DBC=30°.又∵ ∠DBC=∠DAB+∠ADB, ∴ ∠ADB=15°.∴ ∠DAB=∠ADB. ∴ BD=AB=2. 即B ,D 之间的距离为2km .(2)过B 作BO⊥DC,交其延长线于点O , 在Rt△DBO 中,BD=2,∠DBO=60°. ∴ DO=2×sin60°=2×323=,BO=2×cos60°=1. 在Rt△CBO 中,∠CBO=30°,CO=BOtan30°=33, ∴ CD=DO-CO=332333=-(km ). 即C ,D 之间的距离为332km . 22. 解:能够合理装上平行四边形纱窗时的最大高度:960.995.1-=(cm )能够合理装上平行四边形纱窗时的高:96sin α∠或96cos(90)α-∠·° 当81α∠=°时,纱窗高:96sin 81960.98794.75295.1=⨯=<°∴此时纱窗能装进去,当82α∠=°时,纱窗高:96sin82960.99095.0495.1=⨯=<° ∴此时纱窗能装进去.当83α∠=°时,纱窗高:96sin 83960.99395.32895.1=⨯=>° ∴此时纱窗装不进去. 因此能合理装上纱窗时α∠的最大值是82°.。
第25章解直角三角形一、填空题1、若直角三角形两条直角边长分别为5和12,则斜边上的中线长为 ;2、若等腰直角三角形的一边长是2,则它的面积是 ;3、在△ABC 中,∠C=900,a=6,b=8,则sinA= ; 4、在△ABC 中,∠C=900,sinB=135,则cosB= ; 5、若sin α=23,则锐角α= 度; 6、在Rt △ABC 中,∠C=900,a=20,b=220,则∠B= 度; 7、在Rt △ABC 中,∠C=900,sinA=54,AB=10,则AC= ; 8、在离大楼15m 的地面上看大楼顶部仰角为600,则大楼高 m ;9、在电线杆离地面8m 的地方向地面拉一条缆绳以固定电线杆,如果缆绳与地面成600角,则需要缆绳 m (打结部分不计);10、一个斜坡的坡度是1:3,高是4m ,则他从坡底到坡顶部所走的路程是 m ;二、选择题11、直角三角形的两条边长分别是3、4,则第三条边长是( ) A 、5 B 、7 C 、7 D 、5或712、如图,菱形ABCD 的对角线AC=6,BD=8,∠ABD=α,则下列结论正确的是( ) A 、sin α=54 B 、cos α=53 C 、tan α=34 D 、 cot α=34 13、如图,在Rt △ABC 中,∠C=900,BC=4,AC=3,CD ⊥AB 于D ,设∠ACD=α,则cos α的值为( ) A 、54 B 、53 C 、34 D 、 3414、在Rt △ABC 中,∠C=900,且a ≠b ,则下列式子中,不能表示△ABC 面积的是( )A 、ab 21 B 、B ac sin 21 C 、A b tan 212 D 、B A c cos sin 21215、如图,钓鱼竿AC 长为6m ,露在水面上的鱼BC 长为23m ,某钓者想看看鱼钓上的情况,把鱼竿AC 转动到AC ′的位置,此时露在水面 上的鱼线B ′C ′为33m ,则鱼竿转过的角度是( )ABCDABCDABC C ′B ′A 、600B 、450C 、150D 、900三、解答题16、计算: 17、)30sin 60sin 3(30cot 30tan 45cos 45sin 00000202--⋅+18、如图是直线52+-=x y 的图象,求锐角∠OAB 的四个三角函数值,并求∠OAB 的大小。
华师大版九年级(上)中考题单元试卷:第25章解直角三角形(06)一、选择题(共1小题)1.如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC的高度为()A.5米B.6米C.8米D.(3+)米二、填空题(共3小题)2.如图,某登山运动员从营地A沿坡角为30°的斜坡AB到达山顶B,如果AB=2000米,则他实际上升了米.3.如图,有一滑梯AB,其水平宽度AC为5.3米,铅直高度BC为2.8米,则∠A的度数约为(用科学计算器计算,结果精确到0.1°).4.如图是一款可折叠的木制宝宝画板.已知AB=AC=67cm,BC=30cm,则∠ABC的大小约为°(结果保留到1°).三、解答题(共26小题)5.如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B、C在同一水平地面上.(1)求斜坡AB的水平宽度BC;(2)矩形DEFG为长方体货柜的侧面图,其中DE=2.5m,EF=2m,将该货柜沿斜坡向上运送,当BF=3.5m时,求点D离地面的高.(≈2.236,结果精确到0.1m)6.如图,登山缆车从点A出发,途经点B后到达终点C,其中AB段与BC段的运行路程均为200m,且AB段的运行路线与水平面的夹角为30°,BC段的运行路线与水平面的夹角为42°,求缆车从点A运行到点C的垂直上升的距离.(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)7.如图,某水上乐园有一个滑梯AB,高度AC为6米,倾斜角为60°,暑期将至,为改善滑梯AB的安全性能,把倾斜角由60°减至30°(1)求调整后的滑梯AD的长度;(2)调整后的滑梯AD比原滑梯AB增加多少米?(精确到0.1米)(参考数据:≈1.41,,≈2.45)8.某学校的校门是伸缩门(如图1),伸缩门中的每一行菱形有20个,每个菱形边长为30厘米.校门关闭时,每个菱形的锐角度数为60°(如图2);校门打开时,每个菱形的锐角度数从60°缩小为10°(如图3).问:校门打开了多少米?(结果精确到1米,参考数据:sin5°≈0.0872,cos5°≈0.9962,sin10°≈0.1736,cos10°≈0.9848).9.如图,伞不论张开还是收紧,伞柄AP始终平分同一平面内两条伞架所成的角∠BAC,当伞收紧时,结点D与点M重合,且点A、E、D在同一条直线上,已知部分伞架的长度如下:单位:cm伞架DE DF AE AF AB AC长度363636368686(1)求AM的长.(2)当∠BAC=104°时,求AD的长(精确到1cm).备用数据:sin52°=0.788,cos52°=0.6157,tan52°=1.2799.10.已知不等臂跷跷板AB长4m.如图①,当AB的一端A碰到地面上时,AB与地面的夹角为α;如图②,当AB的另一端B碰到地面时,AB与地面的夹角为β.求跷跷板AB 的支撑点O到地面的高度OH.(用含α,β的式子表示)11.如图,A、B两地之间有一座山,汽车原来从A地到B地经过C地沿折线A→C→B行驶,现开通隧道后,汽车直接沿直线AB行驶.已知AC=10千米,∠A=30°,∠B=45°.则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果保留根号)12.海上有一小岛,为了测量小岛两端A、B的距离,测量人员设计了一种测量方法,如图所示,已知B点是CD的中点,E是BA延长线上的一点,测得AE=8.3海里,DE=30海里,且DE⊥EC,cos∠D=.(1)求小岛两端A、B的距离;(2)过点C作CF⊥AB交AB的延长线于点F,求sin∠BCF的值.13.如图,马路的两边CF,DE互相平行,线段CD为人行横道,马路两侧的A,B两点分别表示车站和超市.CD与AB所在直线互相平行,且都与马路的两边垂直,马路宽20米,A,B相距62米,∠A=67°,∠B=37°.(1)求CD与AB之间的距离;(2)某人从车站A出发,沿折线A→D→C→B去超市B.求他沿折线A→D→C→B到达超市比直接横穿马路多走多少米.(参考数据:sin67°≈,cos67°≈,tan67°≈,sin37°≈,cos37°≈,tan37°≈)14.某地下车库出口处“两段式栏杆”如图1所示,点A是栏杆转动的支点,点E是栏杆两段的连接点.当车辆经过时,栏杆AEF升起后的位置如图2所示,其示意图如图3所示,其中AB⊥BC,EF∥BC,∠EAB=143°,AB=AE=1.2米,求当车辆经过时,栏杆EF段距离地面的高度(即直线EF上任意一点到直线BC的距离).(结果精确到0.1米,栏杆宽度忽略不计参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75.)15.如图是某地下商业街的入口,数学课外兴趣小组的同学打算运用所学的知识测量侧面支架的最高点E到地面的距离EF.经测量,支架的立柱BC与地面垂直,即∠BCA=90°,且BC=1.5m,点F、A、C在同一条水平线上,斜杆AB与水平线AC的夹角∠BAC=30°,支撑杆DE⊥AB于点D,该支架的边BE与AB的夹角∠EBD=60°,又测得AD=1m.请你求出该支架的边BE及顶端E到地面的距离EF的长度.16.校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于21米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.(1)求AB的长(精确到0.1米,参考数据:=1.73,=1.41);(2)已知本路段对校车限速为40千米/小时,若测得某辆校车从A到B用时2秒,这辆校车是否超速?说明理由.17.为倡导“低碳生活”,人们常选择以自行车作为代步工具、图(1)所示的是一辆自行车的实物图.图(2)是这辆自行车的部分几何示意图,其中车架档AC与CD的长分别为45cm和60cm,且它们互相垂直,座杆CE的长为20cm.点A、C、E在同一条直线上,且∠CAB=75°.(参考数据:sin75°=0.966,cos75°=0.259,tan75°=3.732)(1)求车架档AD的长;(2)求车座点E到车架档AB的距离(结果精确到1cm).18.九(1)数学兴趣小组为了测量河对岸的古塔A、B的距离,他们在河这边沿着与AB平行的直线l上取相距20m的C、D两点,测得∠ACB=15°,∠BCD=120°,∠ADC=30°,如图所示,求古塔A、B的距离.19.如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=:3.若新坡角外需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:≈1.414,≈1.732)20.如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(参考数据:sin32°≈0.53;cos32°≈0.85;tan32°≈0.62;sin68°≈0.93;cos68°≈0.37;tan68°≈2.48)21.2013年4月20日,四川雅安发生里氏7.0级地震,救援队救援时,利用生命探测仪在某建筑物废墟下方探测到点C处有生命迹象,已知废墟一侧地面上两探测点A、B相距4米,探测线与地面的夹角分别为30°和60°,如图所示,试确定生命所在点C的深度(结果精确到0.1米,参考数据≈1.41,≈1.73)22.图1中的中国结挂件是由四个相同的菱形在顶点处依次串联而成,每相邻两个菱形均成30°的夹角,示意图如图2.在图2中,每个菱形的边长为10cm,锐角为60°.(1)连接CD,EB,猜想它们的位置关系并加以证明;(2)求A,B两点之间的距离(结果取整数,可以使用计算器)(参考数据:≈1.41,≈1.73,≈2.45)23.2013年3月,某煤矿发生瓦斯爆炸,该地救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面A、B两个探测点探测到C处有生命迹象.已知A、B两点相距4米,探测线与地面的夹角分别是30°和45°,试确定生命所在点C的深度.(精确到0.1米,参考数据:)24.如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB 段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).25.“中国﹣益阳”网上消息,益阳市为了改善市区交通状况,计划在康富路的北端修建通往资江北岸的新大桥.如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.求AB的长(精确到0.1米).参考数据:sin76.1°≈0.97,cos76.1°≈0.24,tan76.1°≈4.0;sin68.2°≈0.93,cos68.2°≈0.37,tan68.2°≈2.5.26.我们把“按照某种理想化的要求(或实际可能应用的标准)来反映或概括的表现某一类或一种事物关系结构的数学形式”看作是一个数学中的一个“模式”(我国著名数学家徐利治).如图是一个典型的图形模式,用它可测底部可能达不到的建筑物的高度,用它可测河宽,用它可解决数学中的一些问题.等等.(1)如图,若B1B=30米,∠B1=22°,∠ABC=30°,求AC(精确到1);(参考数据:sin22°≈0.37,cos22°≈0.92,tan22°≈0.40,≈1.73)(2)如图2,若∠ABC=30°,B1B=AB,计算tan15°的值(保留准确值);(3)直接写出tan7.5°的值.(注:若出现双重根式,则无需化简)27.某校数学课题学习小组在“测量教学楼高度”的活动中,设计了以下两种方案:课题测量教学楼高度方案一二图示测得数据CD=6.9m,∠ACG=22°,∠BCG=13°,EF=10m,∠AEB=32°,∠AFB=43°参考sin22°≈0.37,cos22°≈0.93,tan22°≈0.40sin32°≈0.53,cos32°≈0.85,tan32°≈0.62数据sin13°≈0.22,cos13°≈0.97tan13°≈0.23sin43°≈0.68,cos43°≈0.73,tan43°≈0.93请你选择其中的一种方法,求教学楼的高度(结果保留整数)28.如图1,一辆汽车的背面,有一种特殊形状的刮雨器,忽略刮雨器的宽度可抽象为一条折线OAB,如图2所示,量得连杆OA长为10cm,雨刮杆AB长为48cm,∠OAB=120°.若启动一次刮雨器,雨刮杆AB正好扫到水平线CD的位置,如图3所示.(1)求雨刮杆AB旋转的最大角度及O、B两点之间的距离;(结果精确到0.01)(2)求雨刮杆AB扫过的最大面积.(结果保留π的整数倍)(参考数据:sin60°=,cos60°=,tan60°=,≈26.851,可使用科学记算器)29.身高1.65米的兵兵在建筑物前放风筝,风筝不小心挂在了树上.在如图所示的平面图形中,矩形CDEF代表建筑物,兵兵位于建筑物前点B处,风筝挂在建筑物上方的树枝点G处(点G在FE的延长线上).经测量,兵兵与建筑物的距离BC=5米,建筑物底部宽FC=7米,风筝所在点G与建筑物顶点D及风筝线在手中的点A在同一条直线上,点A距地面的高度AB=1.4米,风筝线与水平线夹角为37°.(1)求风筝距地面的高度GF;(2)在建筑物后面有长5米的梯子MN,梯脚M在距墙3米处固定摆放,通过计算说明:若兵兵充分利用梯子和一根5米长的竹竿能否触到挂在树上的风筝?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)30.如图,益阳市梓山湖中有一孤立小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PD,小张在小道上测得如下数据:AB=80.0米,∠P AB=38.5°,∠PBA=26.5°.请帮助小张求出小桥PD的长并确定小桥在小道上的位置.(以A,B为参照点,结果精确到0.1米)(参考数据:sin38.5°=0.62,cos38.5°=0.78,tan38.5°=0.80,sin26.5°=0.45,cos26.5°=0.89,tan26.5°=0.50)华师大版九年级(上)中考题单元试卷:第25章解直角三角形(06)参考答案一、选择题(共1小题)1.A;二、填空题(共3小题)2.1000;3.27.8°;4.77;三、解答题(共26小题)5.;6.;7.;8.;9.;10.;11.;12.;13.;14.;15.;16.;17.;18.;19.;20.;21.;22.;23.;24.;25.;26.;27.;28.;29.;30.;。