高二数学第一次月考试题2012.9

2012-2013学年下期第一次月考试卷高二数学（理科）一、选择题(本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的) 1．设函数0()f x x 在可导，则000()(3)limt f x t f x t t→+--=（ ）A ．'0()f x B ．'02()f x - C ．'04()f x D ．不能确定 2．一物体的运动方程为s ＝2t sin t ＋t ，则它的速度方程 s ′为( )A ．v ＝2sin t ＋2t cos t ＋1B ．v ＝2sin t ＋2t cos tC ．v ＝2sin tD ．v ＝2sin t ＋2cos t ＋13．若曲线y ＝x 2＋ax ＋b 在点(0，b )处的切线方程是x －y ＋1＝0，则( )A ．a ＝1，b ＝1B ．a ＝－1，b ＝1C ．a ＝1，b ＝－1D ．a ＝－1，b ＝－1 4.设函数f （x ）={ EMBED Equation.DSMT4 |2x+lnx 则 （ ） A ．x=为f(x)的极大值点 B ．x=为f(x)的极小值点 C ．x=2为 f(x)的极大值点 D ．x=2为 f(x)的极小值点 5．函数的极大值是A. －B. 1C.D.6．函数f (x )＝x 3＋ax 2＋3x －9，已知f (x )在x ＝－3时取得极值，则a 等于( )A ．2B ．3C ．4D ．57．设f (x )，g (x )分别是定义在R 上的奇函数和偶函数．当x <0时，f ′(x )g (x ) ＋f (x )g ′(x )>0，且g (－3)＝0，则不等式f (x )g (x )<0的解集是( )A ．(－3,0)∪(3，＋∞)B ．(－3,0)∪(0,3)C ．(－∞，－3)∪(3，＋∞)D ．(－∞，－3)∪(0,3)8．积分dxx421等于( )A ．－2ln2B ．2ln2C ．－ln2D ．ln2 9．设函数在定义域内可导，的图象如图所示，则导函数可能为（ ）10．已知三次函数f (x )＝13|x 3－(4m －1)x 2＋(15m 2－2m －7)x ＋2在x ∈(－∞，＋∞)是增函数，则m 的取值范围是( )A ．m <2或m >4B ．－4<m <－2C ．2<m <4D ．以上皆不正确 11．设底面为等边三角形的直棱柱的体积为，则其表面积最小时，底面边长 为（ ）．Ａ． Ｂ． Ｃ． D ． 12.设f (x )、g (x )是定义域为R 的恒大于0的可导函数，且f ′(x )g (x )－ f (x )g ′(x )<0，则当 a <x <b 时有( )A ．f (x )g (x )>f (b )g (b )B ．f (x )g (a )>f (a )g (x )C ．f (x )g (b )>f (b )g (x )D ．f (x )g (x )>f (a )g (x ) 二、填空题(本大题共4个小题，每小题5分，共20分．) 13.曲线在点处的切线方程为___________________xyO图xyOAxyOBxy OC yODx14.若函数f (x )＝ax 2－1x |的单调增区间为(0，＋∞)，则实数a 的取值范围是___.15．已知二次函数的图象如图所示,则它与x 轴所围成封 闭图形的面积为_______16.设曲线y ＝x n ＋1(n ∈N *)在点(1,1)处的切线与x 轴的交点的横坐标为x n ，令a n ＝lg x n ，则 a 1＋a 2＋…＋a 99的值为________．三、解答题(本大题共6个小题，共70分．解答应写出文字说明、证明过程或演算步骤)17．(本题满分10分)求函数的极大值和极小值。

高2012级第一次月考数 学 试 题（理科卷）数学试题卷共4页。

满分150分。

考试时间120分钟。

注意事项：1．答题前，务必将自己的姓名、准考证号填写在答题卡规定的位置上。

2．答选择题时，必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其他答案标号。

3．答非选择题时，必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定的位置上。

4．所有题目必须在答题卡上作答，在试题卷上答题无效。

第Ⅰ卷（选择题 共50分） 一．选择题：(本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的) 1.函数sin 4y x =的周期是 A.2π B.2π C.4πD.4π 2.在α的终边上取一点为()3,4P -，则cos α= A.45 B.35 C.45- D.35- 3.若3cos 2α=，其中(02)απ<<,则角α所有可能的值是A.6π或116π B.6π或76π C.3π或23π D.3π或53π4.已知定义在[1,1]-上的函数()y f x =的值域为[2,0]-,则函数(cos 2)y f x =的值域为 A.[1,1]- B.[3,1]-- C.[2,0]- D.不能确定5.在等差数列{}n a 中,首项14a =-,2d =,则12345a a a a a ++++= A.0 B.10 C.-10 D.126.函数lg(sin )y x =的定义域为 A.2,22k k k Z πππ⎛⎫+∈ ⎪⎝⎭B.()2,2k k k Z πππ+∈ C.2,22k k k Z πππ⎡⎤+∈⎢⎥⎣⎦D.[]2,2k k k Z πππ+∈7.已知函数()213f x ax ax =+-的定义域是R ，则实数a 的取值范围是 A. 13a > B.13a ≤ C.120a -<< D.120a -<≤ 8.函数2cos 1y x =-2()33x ππ-≤≤的值域是 A.[]2,0- B.[]3,0- C.[]2,1- D.[]3,1- 9.函数)62sin(π+-=x y 的单调递减区间是A.2,263k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦B.52,266k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦ C.,63k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦D.5,66k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦10.已知1sin cos 5θθ+=，且θ是第二象限的角，则44sin cos θθ-= A ．125 B ．725- C ．725± D ．725第Ⅱ卷（非选择题 共100分）二．填空题（本大题共5小题，每题5分，满分25分，把答案填写在答题卡相应位置上） 11.在等比数列{}n a 中，24a =,5256a =，则公比q = ． 12.54sin 28tan 45tan 62tan 36sin 22++= ． 13.若3()log (1)f x x =+的反函数为1()y fx -=，则方程1()8f x -=的解x = ．14.设扇形的周长为8cm ，面积为24cm ，则扇形的圆心角的弧度数是 ． 15．给出下列命题：○1不等式12x≥的解集是12x x ⎧⎫≤⎨⎬⎩⎭； ○2若,αβ是第一象限角，且αβ>，则sin sin αβ>；○3tan 20tan 403tan 20tan 403++=；○4()()2sin 31f x x =+的图象可由2sin 3y x =的图象向左平移1个单位得到； ○5函数()cos 2cos sin xf x x x=-的值域是()2,2-.其中正确的命题的序号是____________________(要求写出所有正确命题的序号).三．解答题：（本大题共6小题，共75分，解答应写出文字说明，证明过程或演算步骤） 16．（本小题满分13分）已知()()tan tan sin()cos()2f x x x x x πππ⎛⎫=-++-+⎪⎝⎭. （1）化简()f x ；（2）当tan 2x =时，求()f x 的值.17. （本小题满分13分）已知3sin()5αβ+=，5cos 13β=-；且α为锐角，β为钝角. （1）求cos()αβ+和sin β； （2）求αsin 的值．18. （本小题满分13分）已知函数()sin()cos()f x x x θθ=+++的定义域为R . （1）当0θ=时，求()f x 的单调递减区间； （2）若(0,)θπ∈，当θ为何值时,()f x 为奇函数．19．（本小题满分12分）已知函数()22sin 2sin cos 3cos f x x x x x =++其中x R ∈． （1）求函数()f x 的最小正周期； （2）当0,2x π⎡⎤∈⎢⎥⎣⎦时，求()f x 的值域；20．（本小题满分12分）一般地，对于函数()y f x =，若存在0x R ∈，使00()f x x =成立，则称0x 为()f x 的不动点.若函数2()(1)1f x ax b x b =+++-其中0a ≠. （1）当1a =，2b =-时，求()f x 的不动点；（2）若对于任意实数b ，函数()f x 恒有两个相异的不动点，求a 的取值范围.21. （本小题满分12分）已知函数()44(4)f x x x x =-+≥的反函数为1()fx -，数列{}n a 满足：11a =，()11n n a f a -+=，*n N ∈，数列121321,,,,n n b b b b b b b ----是首项为1，公比为13的等比数列.（1）求证：数列{}na 为等差数列；（2）求数列{}n b 的通项公式；（3）若n n n c b a =，求数列{}n c 的前n 项和n S .数学试题参考答案2010.4.8一.选择题：ABACD BDCCD二.填空题：11．4； 12．2； 13．2； 14． 2； 15．○3、○5 三.解答题： 文16、理16解：（1）()()()cot tan sin cos f x x x x x =+-- 1sin cos x x =+---------------------6分 （2）()22sin cos 1sin cos x x f x x x =++2tan 1tan 1xx =++2271215=+=+---------------------13分 文17、理17 解：（1）0,22ππαβπ<<<<322παβπ∴<+< 又3sin()5αβ+=，5cos 13β=- 4cos()5αβ∴+=-，12sin 13β=---------------------7分 （2）由（1）可知：()()sin()sinααββ=+-354123351351365⎛⎫⎛⎫=⨯---⨯= ⎪ ⎪⎝⎭⎝⎭---------------------13分 文18解：（1）由77S =，1575S =得()17772a a +⨯=，()11515752a a +⨯= 41a =，85a =---------------------6分 （2）由（1）知：8451144a a d --=== ()()441413n a a n d n n ∴=+-=+-⨯=- 12a ∴=-()()1223152222n n a a n n n S n n +-+-∴===----------------------13分文19、理18解：（1）0θ=时，()sin cos 2sin 4f x x x x π⎛⎫=+=+ ⎪⎝⎭又由322242k x k πππππ+≤+≤+，得 52244k x k ππππ+≤≤+ ∴()f x 的单调递减区间为52,244k k ππππ⎡⎤++⎢⎥⎣⎦k Z ∈---------------------6分 （2）()2sin 4f x x πθ⎛⎫=++ ⎪⎝⎭，又若()f x 为奇函数，则(0)0f =sin 04πθ⎛⎫∴+= ⎪⎝⎭又0θπ<<，从而5444ππθπ<+< 4πθπ∴+=即34θπ∴=---------------------12分（理科13分） 文20、理19 解：（1）1cos 21cos 2()sin 2322x xf x x -+=++⨯ sin 2cos 22x x =++2sin 224x π⎛⎫=++ ⎪⎝⎭∴函数()f x 的最小正周期22T ππ==---------------------6分 （2）由（1）知：()2sin 224f x x π⎛⎫=++ ⎪⎝⎭又 0,2x π⎡⎤∈⎢⎥⎣⎦，则 52,444x πππ⎡⎤+∈⎢⎥⎣⎦ 所以 当242x ππ+=，即 8x π=时，()max 22f x =+当5244x ππ+=，即 2x π=时，()min 1f x = 所以，()f x 的值域为1,22⎡⎤+⎣⎦---------------------12分文21、理20解：（1）当1a =，2b =-时，2()3f x x x =--从而00()f x x =可化为20003x x x --=即01x =-或3所以()f x 的不动点为1-或3---------------------4分 （2）由00()f x x =可化为20010ax bx b ++-=函数()f x 恒有两个相异的不动点∴关于0x 的方程20010ax bx b ++-=恒有两不等实根从而0a ≠且()2410b a b ∆=-->对任意实数b 都成立---------------------8分即关于b 的不等式2440b ab a -+>恒成立216160a a ∴∆=-<即01a <<---------------------12分 理21（1）证明：()2()442f x x x x =-+=-由4x ≥，得()0f x ≥ 所以()21()2f x x -=+所以()211()2n n n a f a a -+==+即：12n n a a +=+故数列{}na 是以11a =为首项，2为公差的等差数列---------------------4分（2）由题意知，11b =，1113n n n b b --⎛⎫-= ⎪⎝⎭所以121321()()()n n n b b b b b b b b -=+-+-++-21111311133323n n -⎛⎫⎛⎫⎛⎫=++++=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭所以数列{}n b 的通项公式为31123n n b ⎛⎫=- ⎪⎝⎭---------------------8分 （3）由（1）得：()12121n a n n =+-=-，即：()221n a n =-由（2）得：31123n n b ⎛⎫=- ⎪⎝⎭所以()3121123n n n n c b a n ⎛⎫==-- ⎪⎝⎭12n n S c c c =+++()233135211352123333nn n ⎡-⎤⎛⎫=++++--++++⎪⎢⎥⎝⎭⎣⎦------------------10分 令23135213333n n n T -=++++ 则234111352321333333n n n n n T +--=+++++ 得：23412111112123333333n n n n T +-⎛⎫=+++++- ⎪⎝⎭ 111112113333n n n -+-⎛⎫=+-- ⎪⎝⎭ 所以113n nn T +=- 又()213521n n ++++-=所以231123n n n S n +⎛⎫=-+ ⎪⎝⎭---------------------12分。

1 / 3中学2012-2013学年第一学期高二数学月考试题一、 选择题 （ 本大题共12小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项符合题目的要求，请将答案填写在题后的表格中．）1、若a 与b 是异面直线，且直线c ∥a ，则c 与b 的位置关系是 ( ） A ．相交 B ．异面 C ．平行 D ．异面或相交2、下列说法中正确的是（ ）Ａ平行于同一直线的两个平面平行； Ｂ垂直于同一直线的两个平面平行； Ｃ平行于同一平面的两条直线平行； Ｄ垂直于同一平面的两个平面平行． 3、对于用“斜二侧画法”画平面图形的直观图，下列说法正确的是（ ）A.等腰三角形的直观图仍是等腰三角形B.梯形的直观图可能不是梯形C.正方形的直观图为平行四边形D.正三角形的直观图一定是等腰三角形4、如图，一个空间几何体的直观图的正视图、侧视图、俯视图为全等的等腰直角三角形，如果直角三角形的直角边等1，那么这个几何体的体积为 （ ）A.1 B.21 C.31 D.615、圆锥的底面半径为a ，侧面展开图是半圆面,那么此圆锥的侧面积是 （ ） A ．22a π B ．24a π C ．2aπ D ．23aπ6、设α、β、r 是互不重合的平面，m ，n 是互不重合的直线，给出四个命题： ①若m ⊥α，m ⊥β，则α∥β②若α⊥r ，β⊥r ，则α∥β ③若m ⊥α，m ∥β，则α⊥β④若m ∥α，n ⊥α，则m ⊥n 其中正确命题的个数是（ ）A ．1B ．2C ．3D ．47、△ABC 是边长为1的正三角形，那么△ABC 的斜二测平面直观图C B A '''∆的面积为（ ）A ．43 B ．83 C ．86 D ．166 8、设正方体的表面积为242cm ，一个球内切于该正方体，那么这个球的体积是 （ ）A ．π343cmB ．π63cmC ．π383cm D ．π3323cm 9、如右图，一个空间几何体正视图与左视图为全等的等边三角形，俯视图为一个半径为1的圆及其圆心，那么这个几何体的表面积为 （ ） Ａ．π Ｂ．π3 Ｃ．π2 Ｄ．3+π10、将边长为a 的正方形ABCD 沿对角线AC 折起，折后连结BD ，构成三棱锥D-ABC,若棱BD 的长为22a ．则此时三棱锥D-ABC 的体积是（ ） A ．122a 3 B ．123a 3C ．246a 3D ．61a 311、在ABC ∆中，0120,5.1,2=∠==ABC BC AB （如下图），若将ABC ∆绕直线BC 旋转一周，则所形成的旋转体的体积是（ ）A.29π B.27π C.25π D.23π12、正四棱锥S —ABCD A 、B 、C 、D 都在同一个球面上，则该球的体积为 ( )A 、34πB 、3πC 、 32πD 、38π二、填空题（共4题，各4分，共16分） 13、一个底面直径．．和高．都是4的圆柱的侧面积为． 14、圆锥底面半径为1，其母线与底面所成的角为060，则它的侧面积为__________________． 15、已知△ABC 为直角三角形，且090=∠ACB ，AB=10，点P 是平面ABC 外一点，若PA=PB=PC ，且P Ｏ⊥平面ABC ，Ｏ为垂足，则ＯＣ=__________________．16、若3223===⊥BC AB PA ABCD ABCD PA ，，是矩形，若，且平面，则俯视图左视图正视图正视图 侧视图 俯视图2 / 3CABMPCABMPA BD P --_________三、解答题（共4题，共36分）17、(本题满分9分) 在三棱锥V —ABC 中，VA=VB=AC=BC=2，AB=32，VC=1，求二面角V —AB —C 的大小．18、（本小题满分9分）三棱锥ABC P -中，平面⊥PBC 平面ABC ，PBC ∆是边长为a 的正三角形，90=∠ACB ， 30=∠BAC ，M 是BC 的中点．（1）求证：AC PB ⊥； （2）求点M 到平面PCA 的距离；19、(本题满分9分) 如图，ABCD 是正方形，O 是正方形的中心，PO ⊥底面ABCD ，E 是PC 的中点． 求证：(Ⅰ)PA ∥平面BDE ；(Ⅱ)平面PAC ⊥平面BDE ．20、(本题满分9分) 如图,在三棱锥S-ABC 中，平面SAC ⊥平面ABC ，且△SAC 是正三角形,O 是AC 的中点，D 是AB 的中点．(Ⅰ) 求证：ＯＤ//平面ＳＢＣ； (Ⅱ) 求证:SO ⊥AB .中学2012-2013学年第一学期 高二数学月考试题答题卡一、 选择题 本大题共12小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项符合题目的要求，请将答案填写在题后的表格中． 二、填空题请将答案填写在横线上．（本大题共4小题，每小题4分，共16分） 13、16π14、π2 15、5 16、3三、解答题解答应写出文字说明，证明过程或演算步骤（本大题共4小题，每小题9分，共36分）． 17、(本题满分9分)解：取AB 的中点O ，连接VO ，CO-----------1分因为△V AB 为等腰三角形 ∴VO ⊥AB---------1分 又因为△CAB 为等腰三角形 ∴CO ⊥AB------------1分则∠VOC 为二面角V —AB —C 的平面角-------1分 ∵AB=32，∴AO=3------- 1分 又V A=2则在R t △VOA 中，VO=1------------1分同理可求：CO=1---------------1分 又已知VC=1 则△VOC 为等边三角形，∴∠VOC=060-------------------------------1分 ∴二面角V —AB —C 为060.------------------------------------------1分 18、(本题满分9分)（1）（2）PAC M ACM P V V --=得a h 43=即为M 到平面PAC 的距离题号 1 2 3 4 5 6 7 8 9 10 11 12 答案DBCDACDABCDACBAOS3 / 319、(本题满分9分)证明：（Ⅰ）连结在△P ∵O 是∴OE 分又∵分 P A ⊄分 ∴P A 分 （Ⅱ）∵PO ⊥底面ABCD ，∴PO ⊥BD ．-------------------------------------------------1分 又∵AC ⊥BD ，且AC PO ＝O ，∴BD ⊥平面P AC ．-----------------------------------------1分 而BD ⊂平面BDE ，----------------------------------------1分 ∴平面P AC ⊥平面BDE ．---------------------------------------1分 20、(本题满分9分)(Ⅰ)证明: ∵O 是AC 的中点，D 是AB 的中点∴OD//BC---------------------------------------------------2分又⊂BC 平面SCB------------------------------------------1分OD ⊄平面SCB-------------------------------------------------1分 ∴ＯＤ//平面ＳＢＣ-------------------------------1分 (Ⅱ)证明:SAC ∆是正三角形, O 是AC 的中点，∴SO AC ⊥----------------------------------------------1分又∵平面SAC ⊥平面ABC∴SO ACB ⊥平面------------------------------------2分 ∴SO AB ⊥----------------------------------------------1分CBA O SD。

北师大什邡附校高2012级高二上第一次月考数 学 试 题时间：120分钟 总分：150分一、选择题（本大题10个小题，每题5分，共50分) 1.若向量AB →＝(1,2)，BC →＝(3,4)，则AC →＝( )A ．(4,6)B ．(－4，－6)C ．(－2，－2)D ．(2,2)2．对某商店一个月内每天的顾客人数进行了统计，得到样本的茎叶图(如图1－1所示)，则该样本中的中位数、众数、极差分别是()－1A ．46,45,56B ．46,45,53C ．47,45,56D ．45,47,53 3．为了得到函数2sin(),36xy x R π=+∈的图像，只需把函数2sin ,y x x R =∈的图像上所有的点（ ）A 、向左平移6π个单位长度，再把所得各点的横坐标缩短到原来的13倍（纵坐标不变）B 、向右平移6π个单位长度，再把所得各点的横坐标缩短到原来的13倍（纵坐标不变）C 、向左平移6π个单位长度，再把所得各点的横坐标伸长到原来的3倍（纵坐标不变）D 、向右平移6π个单位长度，再把所得各点的横坐标伸长到原来的3倍（纵坐标不变）4．某几何体的三视图如下，则它的体积是()A ．8－2π3B ．8－π3C ．8－2πD.2π35．已知直线l 1、l 2的方程分别为0=++b ay x ，0=++d cy x ，其图象如图所示，则有( )A ．0<acB ．c a <C ．0<bdD ．d b >6．设a 、b 、c 分别是△ABC 中∠A 、∠B 、∠C 所对边的边长，则直线sinA ·x +a y +c=0与b x -sinB ·y +sinC=0的位置关系是（ ）A ．平行B ．重合C ．垂直D ．相交但不垂直7.给出下列关于互不相同的直线n l m ,, 和平面βα, 的四个命题：①若不共面与则点m l m A A l m ,,,∉=⋂⊂αα；②若l m ,是异面直线，ααα⊥⊥⊥n m n l n m l 则且,,,//,//； ③若m l m l //,//,//,//则βαβα；④若.//,//,//,,,βαββαα则点m l A m l m l =⋂⊂⊂其中为假命题的是（ ）A ．①B ．②C ．③D ．④8．如图，正方体AC 1的棱长为1，过点A 作平面A 1BD 的垂线，垂足为点H ，则以下命题中，错误．．的命题是（ ）A. 点H 是△A 1BD 的垂心B. AH 垂直平面CB 1D 1C. AH 的延长线经过点C 1D. 直线AH 和BB 1所成的角为45º 9．已知集合A ⎭⎬⎫⎩⎨⎧<+=231|x x ，集合B ⎭⎬⎫⎩⎨⎧≥--=02sin |x x x α，且A∩B≠Φ，其中α为直线的倾斜角，则α的取值范围是( ) A ．⎪⎭⎫⎢⎣⎡6,0πB ．⎥⎦⎤⎢⎣⎡6,0π C ．⎪⎭⎫⎝⎛⋃⎪⎭⎫⎢⎣⎡πππ,656,D ．⎪⎭⎫⎝⎛⋃⎪⎭⎫ ⎝⎛πππ,656,0 10.正四面体ABCD 中,E 在棱AB 上, F 在棱CD 上,使得(0)A E C FE BF Dλλ==>,记 ()f λλλαβ=+,其中λα表示EF 和AC 所成的角, λβ表示EF 和BD 所成的角,则( )A 、()(0f λ+∞在，）上单调递增B 、 ()(0f λ+∞在，）上单调递减C 、)(λf 在)1,0(上单调递增，)(λf 在 ),1(+∞上单调递减。

2012届高二下学期第一次月考文、理数学参考答案一、选择题（本大题共有10小题，每小题5分，共50分）CBCBA ，BABDC 二、填空题（共5小题，每小题5分，共25分） 11．12i 12。

23（文） - 2（理） 13。

有关（文） 44+k a 能被4整除（理） 14. 4（文） π（理） 15。

①④三、解答题（4ⅹ12+13+14=75，解答应写出文字说明，证明过程或演算步骤） 16、解:根据韦达定理,满足题意的充要条件是解得-1＜m ＜0,∴当m ∈(-1,0)时,方程的两根异号且和为正.文17、解：（1）若1,,,,2121=+++∈n n a a a R a a a ΛΛ，求证：na a a n 122221≥+++Λ； （2）构造函数22221)()()()(n a x a x a x x f -++-+-=Λ=)(2222212n a a a x nx ++++-Λ，因为对一切R x ∈，恒有0)(≥x f ， 所以由0)(4422221≤+++-=∆n a a a n Λ可得结论na a a n 122221≥+++Λ 理17、解：由题意可设y=f(x)=)0(16)4(2<+-a x a ,把（8，0）代入f(x)=0可得a=-1. 则y=f(x)=x x x 816)4(22+-=+--,(2)易知y=f(x)(x<4)与1l 交点为（1，7），2l 与 y=f(x)交点为（2，12）。

由图形可知S=6]7)8[(12)]8(7[0122=-+-++--⎰⎰dx x x dx x x 。

（3）V=ππ15463])8(7[01222=+--⎰dx x x 18、证明：∵x 、y 、z 均为正数，∴243)2(2222yx y y x y xy x +>++=++，z yy z y z yz y +>++=++243)2(2222，相加即可。

19、解：（1）i a a a a a z z )152(54132221-++-+-=+，又21z z +可以与实数比较大小，则21z z +为实数，则⎪⎩⎪⎨⎧≡-+≠-+015205422a a a a ，得a=3，i z i z +-=-=∴1,8321，则向量21Z Z 对应的复数为z 2-z 1=i 2811+-。

()f x2012-2013学年度第一学期9月月考高二数学试卷注意：1.选择题填在机读卡上2.解答题必须答在相应题号所在位置，否则不予计分，选做题10分记入总成绩，但100分至110分一律记为100分。

第Ⅰ卷一、选择题：本大题共6小题，每小题5分，满分30分．在每小题给出的四个选项中，只有一项是符合题目要求的。

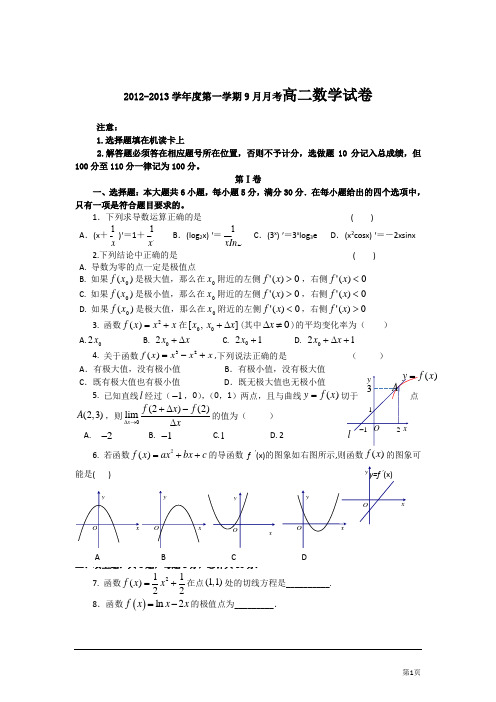
1()A．(x＝1B．(log2x) 'C．(3x) '＝3x log3e D．(x2cosx) '＝－2xsinx2.下列结论中正确的是( )A. 导数为零的点一定是极值点B. 如果)(xf是极大值，那么在x附近的左侧0)('>xf，右侧0)('<xfC. 如果)(xf是极小值，那么在x附近的左侧0)('>xf，右侧0)('<xfD. 如果)(xf是极大值，那么在x附近的左侧0)('<xf，右侧0)('>xf3. 函数2()f x x x=+在[,x]x x+∆(其中0x∆≠)的平均变化率为（）A.2x B.2x x+∆ C. 12+x D.21x x+∆+4. 关于函数32()f x x x x=-+,下列说法正确的是（）A．有极大值，没有极小值B．有极小值，没有极大值C．既有极大值也有极小值D．既无极大值也无极小值5. 已知直线l经过（1-，0），（0，1）两点，且与曲线)(xfy=(2,3)A，则(2)(2)limxf x fx∆→+∆-∆的值为（）A. 2- B. 1- C.1 D. 26. 若函数()f x ax bx c=++2的导函数f ’(x)的图象如右图所示,则函数()f x的图象可7. 函数211()22f x x=+在点(1,1)处的切线方程是__________.8．函数()ln2f x x x=-的极值点为_________．9. （理科）若xxx f 2sin )(=,则=)1('f _________ （文科）若()sin e x f x x =+，则)0('f =________.10.若函数f(x)=x 3+ax-2在区间(1,+ ∞)内是增函数，则实数a 的取值范围是________11．已知函数f (x )＝x 3－3x 的图象与直线y ＝a 有相异三个公共点，则a 的取值范围是________．12.已知f （x ）=x ³-6x ²+9x-abc ，a ＜b ＜c ，且f （a ）=f （b ）=f （c ）=0.现给出如下结论： ①f （0）f （1）＞0；②f （0）f （1）＜0；③f （0）f （3）＞0；④f （0）f （3）＜0.其中正确结论的序号是_________第Ⅱ卷三、解答题：本大题共5小题，共50分．解答应写出文字说明，证明过程或演算步骤．13．（满分10分）已知函数x x x x f 331)(23--=. ( I ) 求()f x 的单调区间；(II) 求()f x 在区间[3,3]-上的最大值和最小值.14．（本小题满分10分）设函数3()3(0)f x x ax b a =-+≠.（Ⅰ）若曲线()y f x =在点(2，f (2) )处与直线8y =相切，求,a b 的值； （Ⅱ）求函数()f x 的单调区间与极值.15．（满分10分）已知函数()x f x e ax =-，a ∈R .（Ⅰ）求函数)(x f 的单调区间；（Ⅱ）当[0,)x ∈+∞时，都有()0f x ≥成立，求实数a 的取值范围.16．（满分10分）已知函数2()ln 20)f x a x a x=+-> (. （Ⅰ）若曲线()y f x =在点(1,(1))P f 处的切线与直线2y x =+垂直，求函数()y f x =的单调区间；（Ⅱ）若对于(0,)x ∀∈+∞都有()2(1)f x a >-成立，试求a 的取值范围；（Ⅲ）记()()()g x f x x b b =+-∈R .当1a =时，函数()g x 在区间1[, ]e e -上有两个零点，求实数b 的取值范围.17（选做10分）. 设函数()(1)ln(1).f x x x =++若对所有的0,x ≥都有()f x ax ≥成立，求实数a 的取值范围高二数学试卷答题纸核分栏第Ⅰ卷选择题答案涂在机读卡上！第Ⅱ卷三、解答题：本大题共5小题，共50分．解答应写出文字说明，证明过程或演算步骤．13．（满分10分）14．（本小题满分10分）15．（本小题满分10分）16．（满分10分）17（选做10分）高二数学试卷答案第Ⅰ卷一、选择题：本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的。

永泰城关中学2011-2012高二数学上学期第一次月考试题（考试时间：120分钟 总分150分）第I 卷（选择题共50分）一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个答案中, 只有一个项是符合题目要求的，把正确的代号填在答题卡指定的位置上。

则c 的值等于（在△/〃&中，若sin A > sin 则A 与B 的人小关系为如果｛心｝为递增数列，则｛a n ｝的通项公式可以为（在等差数列｛①｝中，前四项之和为20,最后四项之和为60,前5项之和是100,则项数A. 5B. 13C. 713D. V372.在等差数列3, 11…中，第5项为（）3. A. 15 B. 18 C. 19D. 23已知中, 5=4,A. 30°B. 30° 或 150°C. 60°D. 60° 或 120°4. A. A>BB. A<B D. A. B 的人小关系不能确定5.A. 色=一2川 + 3B. a H =n 2-3n + \C. %D.6.数列｛色｝满足坷=1耳+]=2色+1 （MG N +）,那么為的值为（）〃+1 A. 4 7, C. 15 D. 317. 在200m 高的山顶上, 测得山下一塔顶与塔底的俯角分别为30°和6（T ,则塔高为,200術A. ---------- m 3B. 400 C • ----- m 38. AABC 中，如果cos A cos B cosC 那么△ABC 是（）A. 宜如三角形B.等边三和形C.等腰直角三和形D.钝和三和形9.1. AABC 中,ZA,B. 8 ZB, ZC 所对的边分别为$b. c.若a = 3、b = 4, ZC= 60°,B. 10C. 11 0. 12 A. 910.设S”为等比数列｛%｝的前〃项和，込+°5=0,则」=（）第II 卷（非选择题共100分）二、填空题：木人题共5小题，每小题4分，共20分，把答案填在答题卡的相应位置。

2011-2012学年度高二上学期第一次月考数学试卷（考试时间120分钟，满分：150分）卷Ⅰ 选择题一、选择题：（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，有且只有一项是符合题目要求的.）1．直线2x ＋ay ＋3＝0的倾斜角为120°，则a 的值是A.233 B ．－233C ．2 3D ．－2 32．直线l 过点(－1,2)且与直线2x －3y ＋4＝0垂直，则l 的方程是A ．3x ＋2y －1＝0B ．3x ＋2y ＋7＝0C ．2x －3y ＋5＝0D ．2x －3y ＋8＝03．经过圆C ：(x ＋1)2＋(y －2)2＝4的圆心且斜率为1的直线方程为 A ．x －y ＋3＝0 B ．x －y －3＝0 C ．x ＋y －1＝0 D ．x ＋y ＋3＝04．圆x 2＋y 2－4x －4y ＋5＝0上的点到直线x ＋y －9＝0的最大距离与最小距离的差为A. 3 B ．2 3 C ．3 3 D ．65．方程2x 2＋ky 2＝1表示的曲线是长轴在y 轴上的椭圆，则实数k 的取值范围是 A ．(0，＋∞) B ．(2，＋∞) C ．(0,2) D ．(0，2) 6．圆221:20O x y x +-=和圆222:40O x y y +-=的位置关系是.A 相离.B 相交 .C 外切 .D 内切7．若椭圆x 25＋y 2m ＝1的离心率e ＝105，则m 的值为A ．1 B.15或5315 C.15D ．3或2538．已知两点M （－2，0），N （2，0），点P 满足⋅=12，则点P 的轨迹方程为A ．11622=+y xB ．822=-x yC ． 1622=+y xD ．822=+y x9．如果直线12,l l 的斜率分别为二次方程2410x x -+=的两个根，那么1l 与2l 的夹角为A ．3π B ．4π C ．6π D ．8π10．椭圆x 24＋y 23＝1的左、右焦点是F 1、F 2，P 是椭圆上一点，若|PF 1|＝3|PF 2|，则P 点到左准线的距离是A ．8B ．6C ．4D ．211．F 1，F 2是椭圆C ：x 28＋y24＝1的两个焦点，在C 上满足PF 1⊥PF 2的点P 的个数为A ．4B ．2C ．1D ．0 12．若直线220(,0)ax by a b +-=>始终平分圆224280x y x y +---=的周长，则12a b+ 的最小值为A ．1B ．5C． D．3+卷Ⅱ 非选择题二、填空题：（本大题共4小题，每小题5分，共20分）13．已知直线0125=++a y x 与圆0222=+-y x x 相切，则a 的值为________.14．若椭圆长轴长与短轴长之比为2，它的一个焦点是(215，0)，则椭圆的标准方程是15．将参数方程⎩⎨⎧=+=θθsin 2cos 21y x （θ为参数）化为普通方程，所得方程是_____.16．设1,m >在约束条件1y xy mx x y ≥⎧⎪≤⎨⎪+≤⎩下，目标函数5z x y =+的最大值为4，则m 的值为 ．三、解答题：（本大题共6小题，共70分. 解答应写出文字说明，证明过程或演算步骤.）17. (本小题满分10分）已知直线l 1的方程为3x ＋4y －12＝0.(1)若直线l 2与l 1平行，且过点(－1,3)，求直线l 2的方程；(2)若直线l 2与l 1垂直，且l 2与两坐标轴围成的三角形面积为4，求直线l 2的方程．18. (本小题满分12分)椭圆的中心在原点，焦点在x 轴上，焦距为2，且经过点A )23,1(-； （1）求满足条件的椭圆方程；（2）求该椭圆的顶点坐标，长轴长，短轴长，离心率．19. (本小题满分12分）设圆满足：①截y 轴所得弦长为2；②被x 轴分成两段圆弧，其弧长之比为3：1；③圆心到直线:20l x y -=，求该圆的方程．20. (本小题满分12分）营养师要求为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物，6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物，6个单位的蛋白质和10个单位的维生素C.另外，该儿童这两餐需要的营状中至少含64个单位的碳水化合物和42个单位的蛋白质和54个单位的维生素C.如果一个单位的午餐、晚餐的费用分别是2.5元和4元，那么要满足上述的营养要求，并且花费最少，应当为该儿童分别预订多少个单位的午餐和晚餐？21.（本小题满分12分）设M 是圆22680x y x y +--=上的动点，O 是原点，N 是射线OM 上的点， 若150||||=⋅ON OM ，求点N 的轨迹方程。

附属高中2011—2012年度高二第二学期第一次月考文科数学试卷命题人：李彦宏 审题人：郝建英班级 姓名 学号 分数一、选择题（每题5分，共60分） 1.复数2211(1)(1)i i i i -++=+-( )A ．iB ．－ｉC ．—１D ．１ 2. “因对数函数log a y x =是增函数（大前提），而1log yx=是对数函数（小前提），所以1log yx=是增函数（结论）．”上面的推理的错误是（ ） A ．大前提错导致结论错 B ．小前提错导致结论错C ．推理形式错导致结论错D ．大前提和小前提都错导致结论错3. 下列有关样本相关系数的说法不正确的是（ ）Ａ．相关系数用来衡量 两个随机变量x 与y 的之间的线性相关程度 Ｂ． 1r ≤，且r 越接近0，相关程度越小 Ｃ． 1r ≤，且r 越接近1，相关程度越大 Ｄ． 1r ≥，且r 越接近1，相关程度越大 4. 下面几种推理是合情推理的是 ( )（1）由正三角形的性质，推测正四面体的性质；（2）由平行四边形、梯形内角和是360︒，归纳出所有四边形的内角和都是360︒； （3）某次考试金卫同学成绩是90分，由此推出全班同学成绩都是90分；（4）三角形内角和是180︒，四边形内角和是360︒，五边形内角和是540︒，由此得凸多边形内角和是180)2⋅-n （ A ．（1）（2） B ．（1）（3） C ．（1）（2）（4） D ．（2）（4）5. 用反证法证明命题“如果a b >( )A ． =B ．<C ． =且<D ．=<6. 已知02a <<，复数z 的实部为a ，虚部为1，则||z 的取值范围是（ ）A ．(1,5)B ．(1,3)C ．(1,D ．(1,7. 已知x 与y 之间的一组数据：A ．（0.5，3） B．（1.5，0） C ．（1，2） D ．（1.5，4） 8. 设P =Q =-，R =，则P ，Q ，R 的大小顺序是（ ）A ．P Q R >>B ．P R Q >>C ．QP R >> D ．Q R P >>9. 若,x y R ∈，且满足32x y +=，则3271x y ++的最小值是（ ） A ．B ．1+C ．6D ．710. 一位同学画出如下若干个圈：○●○○●○○○●○○○○●○○○○○●……．如果将此若干个圈依此规律继续下去，得到一系列的圈，那么在前120个圈中的●的个数是（ ） A ．12B ．13C ．14D ．1511. 如右图，A 、B 是⊙O 上的两点，AC 是⊙O 的切线， ∠B=70°，则∠BAC 等于（ ） A. 70°B. 35°C. 20°D. 10°12. 不等式3529x ≤-<的解集为（ ）A ．[2,1)[4,7)-B ．(2,1](4,7]-C ．(2,1][4,7)--D ．(2,1][4,7)- 二、填空题（每题5分，共20分）13. 若复数z (1)(2)m m i =-++对应的点在直线220x y --=上，则实数m 的值 14. 按流程图的程序计算，若开始输入的值为3x =，则输出的x 的值是15⊙O 的两条弦AB 、CD 相交于点P ，已知AP=2cm ，BP=6cm ，CP ︰PD =1︰3，则DP=___________．16. 函数46y x x =-+-的最小值为AC附属高中2011—2012年度高二第二学期第一次月考文科数学试卷命题人：李彦宏审题人：郝建英班级姓名学号分数一、选择题（每题5分，共60分）二、填空题（每题5分，共20分）13. 14.15. 16.三、解答题（每题14分，共70分，其中第21题，第22题任选一题作答）17. 实数m取什么值时，复数z=(m2-5m+6)+(m2-3m)i是实数？虚数？(14分)18. ①求函数y=（7分）②在数列{a n }中，)(22,111++∈+==N n a a a a nn n ，试猜想数列的通项公式。

高二年级2011-2012学年第二学期第一次月考数学试题（文科）参考公式))()()(()(2d b c a d c b a bc ad n k ++++-=一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是最符合题目要求的.)1、复数i a b +与复数i c d +（a 、b 、c 、d R ∈）的积是实数的充要条件是 ( )A.0ad bc +=B.0ac bd +=C.ac bd =D.ad bc =2、函数)22(9323<<---=x x x x y 有( )A.极大值5,极小值 2-B.极大值5,极小值22-C.极大值5,无极小值D.极小值27-,无极大值315cos 415sin 2==，a 与b 的夹角为30°，则a b 的值为（ ）.(A)21 (B) 23 (C) 3 (D) 324.身高与体重有关系可以用（ ）分析来分析A.殘差B.回归C.二维条形图D.独立检验5、(1)已知332p q +=,求证2p q +≤,用反证法证明时,可假设2p q +≥;(2)已知a b ∈R ，,1a b +<,求证方程20x ax b ++=的两根的绝对值都小于1.用反证法证明时可假设方程有一根1x 的绝对值大于或等于1,即假设11x ≥,以下结论正确的是( )A.(1)的假设错误,(2)的假设正确B.(1)与(2)的假设都正确C.(1)的假设正确,(2)的假设错误D.(1)与(2)的假设都错误6、有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线b ⊂/平面α,直线a ⊂平面α,直线b ∥平面α,则直线b ∥直线a ”的结论显然是错误的,这是因为( )A.大前提错误B.小前提错误C.推理形式错误D.非以上错误7、工人月工资（元）依劳动生产率（千元）变化的回归直线方程为ˆ6090yx =+，下列判断正确的是（ ）A.劳动生产率为1000元时，工资为50元B.劳动生产率提高1000元时，工资提高150元C.劳动生产率提高1000元时，工资提高90元D.劳动生产率为1000元时，工资为90元 8、如右表中给出五组数据),(y x ，从中选出四组使其线性相关最大，且保留第一组)3,5(--，那么，应去掉第（ ）组。