第5章_梁的弯曲
- 格式:doc
- 大小:639.00 KB
- 文档页数:13





第五章 弯曲内力与应力 §5—1 工程实例、基本概念一、实例工厂厂房的天车大梁,火车的轮轴,楼房的横梁,阳台的挑梁等。
二、弯曲的概念:受力特点——作用于杆件上的外力都垂直于杆的轴线。
变形特点——杆轴线由直线变为一条平面的曲线。
三、梁的概念:主要产生弯曲变形的杆。
四、平面弯曲的概念:受力特点——作用于杆件上的外力都垂直于杆的轴线,且都在梁的纵向对称平面内(通过或平行形心主轴且过弯曲中心)。
变形特点——杆的轴线在梁的纵向对称面内由直线变为一条平面曲线。
五、弯曲的分类:1、按杆的形状分——直杆的弯曲;曲杆的弯曲。
2、按杆的长短分——细长杆的弯曲;短粗杆的弯曲。
3、按杆的横截面有无对称轴分——有对称轴的弯曲;无对称轴的弯曲。
4、按杆的变形分——平面弯曲;斜弯曲;弹性弯曲;塑性弯曲。
5、按杆的横截面上的应力分——纯弯曲;横力弯曲。
六、梁、荷载及支座的简化(一)、简化的原则:便于计算,且符合实际要求。
(二)、梁的简化:以梁的轴线代替梁本身。
(三)、荷载的简化:1、集中力——荷载作用的范围与整个杆的长度相比非常小时。
2、分布力——荷载作用的范围与整个杆的长度相比不很小时。
3、集中力偶(分布力偶)——作用于杆的纵向对称面内的力偶。
(四)、支座的简化:1、固定端——有三个约束反力。
2、固定铰支座——有二个约束反力。
3、可动铰支座——有一个约束反力。
(五)、梁的三种基本形式:1、悬臂梁:2、简支梁:3、外伸梁:(L 称为梁的跨长) (六)、静定梁与超静定梁静定梁:由静力学方程可求出支反力,如上述三种基本形式的静定梁。
超静定梁:由静力学方程不可求出支反力或不能求出全部支反力。
§5—2 弯曲内力与内力图一、内力的确定(截面法):[举例]已知:如图,F ,a ,l 。
求:距A 端x 处截面上内力。
解:①求外力la l F Y l FaF m F X AYBY A AX)(F, 0 , 00 , 0-=∴==∴==∴=∑∑∑ F AX =0 以后可省略不求 ②求内力xF M m l a l F F F Y AY C AY s ⋅=∴=-==∴=∑∑ , 0)( , 0∴ 弯曲构件内力:剪力和弯矩1. 弯矩:M ;构件受弯时,横截面上存在垂直于截面的内力偶矩。





第五章弯曲应力第五章 弯曲应力内容提要一、梁的正应力Ⅰ、纯弯曲和横力弯曲纯弯曲:梁横截面上的剪力为零,弯矩为常量,这种弯曲称为纯弯曲。
横力弯曲:梁横截面上同时有剪力和弯矩,且弯矩为横截面位置x 的函数,这种弯曲称为横力弯曲。
Ⅱ、纯弯曲梁正应力的分析方法:1. 观察表面变形情况,作出平面假设,由此导出变形的几何方程;2. 在线弹性范围内,利用胡克定律,得到正应力的分布规律;3. 由静力学关系得出正应力公式。
Ⅲ、中性层和中性轴中性层:梁变形时,其中间有一层纵向线段的长度不变,这一层称为中性层。
中性轴:中性层和横截面的交线称为中性轴,梁发生弯曲变形时横截面就是绕中性轴转动的,在线弹性范围内,中性轴通过横截面的形心。
中性层的曲率,平面弯曲时中性层的曲率为()()1zM x x EI ρ=(5-1) 式中:()x ρ为变形后中性层的曲率半径,()M x 为弯矩,z EI 为梁的弯曲刚度。
(5-1)式表示梁弯曲变形的程度。
Ⅳ、梁的正应力公式1. 横截面上任一点的正应力为zMyI σ=(5-2)正应力的大小与该点到中性轴z 的距离y 成正比,试中M 和y 均取其绝对值,可根据梁的变形情况判断σ是拉应力或压应力。
2. 横截面上的最大正应力,为maxmax z My I σ=(5-3) maxzz I W y =(5-4) z W 为弯曲截面系数,对于矩形、圆形和弯环截面等,z W 的公式应熟记。
3. 弯曲正应力公式的适用范围:1)在线弹性范围内()p σσ≤,在小变形条件下的平面弯曲弯。
2)纯弯曲时,平面假设成立,公式为精确公式。
横力弯曲时,平面假设不成立,公式为近似公式,当梁的跨高比5lh≥时,误差2%≤。
Ⅴ、梁的正应力强度条件 拉、压强度相等的等截面梁[]maxmax zM W σσ=≤ (5-5) 式中,[]σ为料的许用正应力。
当梁内,max ,max t c σσ≠,且材料的[][]t c σσ≠时,强度条件应为[],max t t σσ≤,[],max c σσ≤Ⅵ、提高梁正应力强度的措施1)设法降低最大弯矩值,而提高横截面的弯曲截面系数。
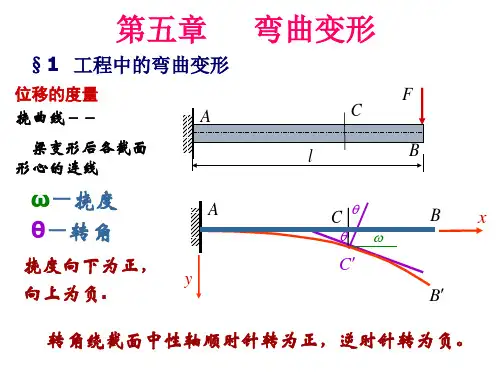
材料力学(土)笔记第五章 梁弯曲时的位移1.梁的位移——挠度及转角为研究等直梁在对称弯曲时的位移取梁在变形前的轴线为x 轴,梁横截面的铅垂对称轴为y 轴而xy 平面即为梁上荷载作用的纵向对称平面梁发生对称弯曲变形后,其轴线将变成在xy 平面内的曲线1AC B度量梁变形后横截面位移的两个基本量是挠度:横截面形心(即轴线上的点)在垂直于x 轴方向的线位移ω转角:横截面对其原来位置的角位移θ 梁变形后的轴线是一条光滑的连续曲线,且横截面仍与该曲线保持垂直因此横截面的转角θ也就是曲线在该点处的切线与x 轴之间的夹角度量等直梁弯曲变形程度的是曲线的曲率梁的变形还受到支座约束的影响通常就用这两个位移量来反映梁的变形情况梁轴线弯曲成曲线后,在x 轴方向也将发生线位移 但在小变形情况下,梁的挠度远小于跨长,梁变形后的轴线是一条平坦的曲线横截面形心沿x 轴方向的线位移与挠度相比属于高阶微量,可略去不记因此在选定坐标后,梁变形后的轴线可表达为()f x ω=式中,x 为梁在变形前轴线上任一点的横坐标;ω为该点的挠度梁变形后的轴线称为挠曲线,在线弹性范围内,也称为弹性曲线上述表达式则称为挠曲线(或弹性曲线)方程由于挠曲线为一平坦曲线,故转角θ可表达为''tan ()f x θθω≈== 称为转角方程即挠曲线上任一点处的切线斜率'ω可足够精确地代表该点处横截面的转角θ 由此可见,求得挠曲线方程后,就能确定梁任一横截面挠度的大小,指向及转角的数值 正值的挠度向下,负值的挠度向上正值的转角为逆时针转向,负值的转角为顺时针方向2.梁的挠曲线近似微分方程及其积分为求得梁的挠曲线方程,利用曲率κ与弯矩M 间的物理关系,即 1M EIκρ== 式中曲率κ为度量挠曲线弯曲程度的量,是非负的这是梁在线弹性范围内纯弯曲情况下的曲率表达式在横力弯曲时,梁横截面上除弯矩M 外尚有剪力S F 但工程用梁,其跨长l 一般均大于横截面高度的10倍剪力S F 对于梁位移的影响很小,可略去不计,故该式子依然适用式中的M 和ρ均为x 的函数,即1()()()M x x x EIκρ== 在数学中,平面曲线的曲率与曲线方程导数间的关系有'''23/21()(1)x ωρω=±+ 取x 轴向右为正,y 轴向下为正时曲线凸向上时''ω为正,凸向下时为负而按弯矩的正、负号规定,梁弯曲后凸向下时为正,凸向上为负,符号相反于是得到 '''23/2()(1)M x EIωω=-+ 由于梁的挠曲线为一平坦曲线,因此,'2ω与1相比十分微小可以略去不计故上式可近似的写为 ''()M x EIω=-上式略去了剪力S F 的影响,并略去了'2ω项 故称为梁的挠曲线近似微分方程若为等截面直梁,其弯曲刚度EI 为一常量,上式可改写为''()EI M x ω=-对于等直梁,上式进行积分,并通过由梁的变形相容条件给出的边界条件确定积分常数 即可求得梁的挠曲线方程当全梁各横截面上的弯矩可用单一的弯矩方程表示时,梁的挠曲线近似微分方程仅有一个 将上式的两端各乘以dx ,经积分一次,得'1()EI M x dx C ω=-+⎰再积分一次,即得12[()]EI M x dx dx C x C ω=-++⎰两式子中积分常数1C 、2C 可通过挠曲线的边界条件确定例如在简支梁中,左右铰支座处的挠度均等于零在悬臂梁中,固定端处的挠度和转角均等于零确定积分常数1C 、2C 后,就分别得到梁的转角方程和挠曲线方程从而可以确定任一横截面的转角和挠度1C 和2C 的几何意义 由于以x 为自变量,在坐标原点即0x =处的定积分恒等于零因此,积分常数'100x C EI EI ωθ===,20C EI ω=式中,0θ和0ω分别表示坐标原点处截面的转角和挠度若梁上的荷载不连续即分布荷载在跨度中间的某点处开始或结束,以及集中荷载或集中力偶作用处梁的弯矩需分段写出,各段梁的挠曲线近似微分方程也随之不同在对各段梁的近似微分方程积分时,均将出现两个积分常数为确定这些积分常数,除需利用支座处的约束条件外还需利用相邻两段梁在交界处位移的连续条件例如左、右两段梁在交界处的截面应具有相等的挠度和转角不论是约束条件和连续条件,均发生在各段挠曲线的边界处故均成为边界条件,即弯曲位移中的变形相容条件遵循两个原则①对各段梁,都是从同一坐标原点到截面之间的梁段上的外力列出弯矩方程所以后一段梁的弯矩方程包括前一段的弯矩方程的新增的()x a -项②对()x a -项的积分,以()x a -作为自变量于是由x a =处的连续条件,就能得到两段梁上相应的积分常数分别相等的结果 对于弯矩方程需分为任意几段的情况,只要遵循上述规则同样可以得到各梁段上相应的积分常数分别相等的结果从而简化确定积分常数的运算3.按叠加原理计算梁的挠度和转角梁在微小变形条件下,其弯矩与荷载成线性关系 在线弹性范围内,挠曲线的曲率与弯矩成正比当挠度很小时,曲率与挠度间呈线性关系梁的挠度和转角均与作用在梁上的荷载成线性关系在这种情况下梁在几项荷载(如集中力、集中力偶或分布力)同时作用下某一横截面的挠度或转角 就分别等于每项荷载单独作用下该截面的挠度或转角的叠加,即为叠加原理 已知梁在每项荷载单独作用下的挠度和转角表则按叠加原理来计算梁的最大挠度和最大转角将较为方便4.奇异函数·梁挠曲线的初参数方程5.梁的刚度校核·提高梁的刚度的措施5.1 梁的刚度校核对于梁的挠度,其许可值通常用许可挠度与跨长之比值[]l ω作为标准 梁的刚度条件可表达为 max[]ll ωω≤ max []θθ≤ 一般土建工程中的构件,强度要求是主要的刚度要求一般处于从属地位但当对构件的位移限制很严,或按强度条件所选用的构件截面过于单薄时刚度条件也可能起控制作用5.2 提高梁的刚度的措施由梁的位移表可见梁的位移(挠度和转角)除了与梁的支承和荷载情况有关还与其弯曲刚度EI 成反比,与跨长l 的n 次幂成正比减小梁的位移,可采取下列措施①增大梁的弯曲刚度EI②调整跨长和改变结构5.梁内的弯曲应变能当梁弯曲时,梁内将积蓄应变能梁在线弹性变形过程中弯曲应变能V ε在数值上等于作用在梁上的外力所作的功W梁在纯弯曲时各横截面上的弯矩M 为常数,并等于外力偶矩e M当梁处于线弹性范围内e EI EI θρ=== θ与e M 呈线性关系直线下的三角形面积就代表外力偶所作的功W ,即12e W M θ=从而得纯弯曲时梁的弯曲应变能 12e V M εθ=即得2222e M l M l V EI EIε== 横力弯曲时,梁内应变能包含两个部分:与弯曲变形相应的弯曲应变能和与切应变形相应的剪切应变能对于弯曲应变能,取长为dx 的梁段,其相邻两横截面的弯矩应分别为()M x 和()()M x dM x +在计算微段的应变能时,弯矩的增量为一阶无穷小,可略去不计 计算器弯曲应变能为2()2M x dV dx EIε= 全梁的弯曲应变能则可通过积分求得为2()2l M x V dx EIε=⎰ 式中,()M x 为梁任一横截面上的弯矩表达式 当各段梁的弯矩表达式不同时,积分需分段进行梁的剪切应变能远小于弯曲应变能,可略去不计。
第5章 梁的弯曲简单起见,本节仅考虑直梁、且梁的轴线与x 轴重合。
1 梁弯曲的基本方程5.1.1 杆的弯曲假定以下我们分三部分来叙述杆的弯曲假定。
(1)平面假定在y M 和z M 的共同作用下,杆件上的d x 微段的两截面将发生(绕形心的)相对转动。
平面假定:杆横截面在变形后仍保持平面。
设微段的一侧截面不动,根据平面假定,另一侧截面将发生两种相对位移(见下图):图5.1在y M 作用下绕 y 轴的转动:d (d )y u z θ= 在z M 作用下绕 z 轴的转动:d (d )z u y θ=- 由于上述两种位移都很小,所以总的轴向位移d u 为d (d )(d )y z u z y θθ=-(5.1.1)其中d y θ和d z θ为d x 微段两截面分别绕y 轴和z 轴相对转过的角度,从而正应变为: x y zu z yx ερρ∂==-∂ (5.1.2)其中d d y yxρθ=——梁轴线在x-z 坐标面内弯曲的曲率半径; d d z zxρθ=——梁轴线在x-y 坐标面内弯曲的曲率半径。
注意,在轴线上0x ε=,这是由于我们只考虑弯曲变形、而没有考虑拉伸变形,从而假定中的截面只绕形心转动,而没有轴向平动。
(2)横向挤压应力为零假定横向挤压应力为零假定: 假定y σ和z σ可以忽略。
这个假定使得我们可以利用单向拉(压)的胡克定律x x yzEEE z y σερρ==-(5.1.3)由此可以计算内力:11x x yzAyzF dA ES ES σρρ==-⎰N (5.1.4)11y x yyzAyzM zdA EI EI σρρ==-⎰ (5.1.5)11z x yzzAyzM ydA EI EI σρρ=-=-+⎰ (5.1.6)其中22d , dd , d , d y z AAy z yz AAAS z A S y A I z A I y A I yz A=====⎰⎰⎰⎰⎰分别是横截面对 y z 、轴的静矩,对 y z 、轴的惯性矩和惯性积。
对于确定的截面,这些量均为已知。
如果截面上的坐标轴取形心主轴(即原点在形心、坐标轴为惯性主轴),则 0y z S S ==, 0yz I =从而N 0x F =从式(5.1.5)、(5.1.6)直接解得11,y zy yzzM M EI EI ρρ== (5.1.7)代入式(5.1.3)得y z x yzM z M yI I σ=-(5.1.8)这样,当弯矩y M 和z M 给定后,轴向应力x σ的分布就给定了。
上述各式中的y EI 和z EI 分别称为杆在两个坐标平面内的抗弯刚度。
(3)直法线假定现在我们来研究曲率半径y ρ和z ρ与形心位移之间的关系。
设轴线由各截面的形心连接而成,轴线上的横向位移在坐标系(以后我们均取形心主轴坐标系)上的分量分别为0()v x 和0()w x 。
显然,轴线上的位移仅仅是一个变量x 的函数,现在的问题是:如何将轴线外的点的位移用形心上的位移函数来表示?直法线假定: 杆的轴线上任一法线,在变形后仍是变形后轴线的法线,而且法线不产生任何的伸缩。
先考虑x-y 平面内的弯曲变形。
这里有两个位移函数(,)(,)u x y v x y 和。
由于法线不伸缩,所以0y ε=,即0(,)(,0)()v x y v x v x ==此外,由于0()v x 的存在使法线产生了0d d z v xθ≈的转动,从而d (,)d v u x y yx=-图5.2类似地,可以考虑x-z 平面内的弯曲变形:00d (,)(), (,)d ww x z w x u x z z x==-这样,杆上任意一点的位移可以写成0000d d (,,)d d (,,)() (,,)() v w u x y z yz x x v x y z v x w x y z w x ⎫=--⎪⎪⎪⎪⎬=⎪⎪⎪=⎪⎭(5.1.9)从而220022d d d d x v w uy z x x xε∂==--∂(5.1.10)将此式与式(5.1.2)比较220022d d 11 , d d y z w v x x ρρ=-= (5.1.11)如果用微分几何来准确计算曲率半径()0322011yw "w 'ρ-=+当01w ' 时,化为(5.1.11)式。
这样,引入直法线假定后,我们可以把整个杆内的位移问题(从而应变问题、应力问题)归结为求轴线上的函数0()v x 和0()w x 。
这里两个函数只与横向位移有关,称为杆的挠度,杆的挠度是由弯曲变形引起的。
为方便见,以后将挠度函数的下角标 “0”省略。
至此,杆件弯曲的三条假定已介绍完,但尚有三个问题需要说明:● 假定(1)实际上已包含在假定(3)之中,因为曲线上任一点的法线全体构成一平面(法平面),所以变形前轴线的法平面(即横截面)在变形后仍是法平面,自动满足假定(1)。
反过来却不一定成立,因为按假定(3),横截面变形后仍是轴线的法平面,但按假定(1)尽管仍是平面,但不一定是法平面。
一组完备的杆的弯曲假定,只须保留(2)和(3)两个假定,称为欧拉—伯努利梁(Euler-Bernoulli )。
● 在上述假定下,Q Qz 0, 0y x F F M ===。
其原因是,由于这三个内力是由横截面上的切应力xy τ和xz τ直接引起的,所以只要考虑这两个应力分量即可。
将式(5.1.9)代入应变表达式:00d d 0d d xy v v u vy x x xγ∂∂=+=-+=∂∂ 00d d 0d d xz w w u w z x x xγ∂∂=+=-+=∂∂ 再由广义胡克定律可得0xy xz ττ==,从而横向剪力和扭矩为零。
● 以上假定是否符合实际情况?根据更精确的弹性力学计算证明,在均匀直杆且只有纯弯矩(横向剪力为零)作用下,由上述假定得到的解与弹性力学的准确解完全一致,当然这里要求外加力矩按式(5.1.8)分布的集度作用到杆件上去。
如果外力分布与式(5.1.8)不一致,则可以引用圣维南原理:除加力截面附近外,其余杆中的应力分布(从而是位移)和准确解基本一致。
事实上,上述假定可以应用到更广泛的范围:对细长杆来说,如果除y M 和z M 外,还有剪力Q x F 和Q y F ,则上述诸式仍适用,这是由于剪切应变能远小于弯曲应变能,从而其对挠度的贡献也远小于弯曲的贡献。
当然这里也有一个矛盾:按上述假定,所有切应变为零,从而根据胡克定律,所有切应力亦为零,这与剪力存在矛盾。
后面我们将另找途径解决。
5.1.2 梁弯曲的基本方程我们用一般的弹性力学变分原理加上前面导出的假定,可以导出梁弯曲的基本方程和边界条件。
由基本假定可得00000d d (,,),(,,)() ,(,,)()d d y z v wu x y z y z v x y z v x w x y z w x x xσσ===--== (5.1.12)由于假定中同时含有应力假定和位移假定(直法线假定),所以选用以应力和位移作为变量的二类变量广义变分原理,现选用二类变量广义余能原理(2.1)122(,){((()))[()]}d ()()d [()]d 0T T T T T B B VB BδδδδδΩ∂Γ=-∇+∇+Ω∂+---=⎰⎰⎰⎰⎰⎰⎰u E u E f u u u E n E n p u σσσσσσ (5.1.13)由(())0T T V∂-∇=∂E u σ可得 ,0x x xy yz zx E σετττ==== (5.1.14)用上标“s ” 记梁的侧面,“e ”记梁的端面。
假定20in ,0on sx p B =Ω=f ,200000000002200000220[()]d [()]d d d d ()d d d d d d d d d ()d (+)d d d d d d d d d [()+()]d ()d d d d sT TB ll T x l l y z y z l y y l z z y z B v w x y z A x s x x xM M v w x q v q w x x x x x M M M M q v q w x v w x x x x δδσδδδδδδδδδδδΩ∇Ω--∂=--+∂=-+=-+++-⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰E u E n p u p u σσ1100000000()()d d d d d [()d d d d +()+()]d e e TB x B xy xz x B v w v wyz y z x x x xv v w w n Bδδσδτδτ-=--++--⎰⎰⎰⎰u u E n σ ()()2200000000000000d d [()]d ()d d d d [()()()()]d d d d d ()d d d d d d d d ()()d de e y TlzB x x x y z B y l zz x z y x y y zx y x z M M B v w x xv wn p yz p v p w B x xM M v w x xv w M n M M n M x xM M n F v n F w x xδδδσδδδδδδδδδ---=---+-+---=----++-⎰⎰⎰⎰E n p u σ式中d ,d y y z z q p s q p s ==⎰⎰d ,d ,d ,d z x y x y y z z M yp A M zp A F p A F p A =-===⎰⎰⎰⎰⎰⎰⎰⎰代入(5.1.13) 即得2222d d :0,0d d y zy z M M q q x x Ω-+=+= (5.1.14)000010000d d d d :,,,d d d d e v v w w B v v w w x x x x==== (5.1.15) 2d d :,,,d d y e zz x z y x y x y x z M M B M n M M n M n F n F xx===-= (5.1.16)此外,由(5.1.16) 最后两式可定义 Q Q d d :,d d y zy z M M F F xxΩ=-=(5.1.17)加上由(5.1.14) 的本构关系(写成内力形式)22022d d :, d d y y z z w v M EI M EI x xΩ=-= (5.1.18)可以得到所有方程和边界条件。
为方便计,我们在下文中将挠度函数的下标“0”省略。
由于可以把梁(杆件)的弯曲变形分解成x-y 平面和x-z 平面内的弯曲,分别求解后,再把相应的结果叠加;所以下面只考虑x-y 平面内的弯曲,而x-z 平面内的弯曲可以仿照计算。