梁的弯曲

梁弯曲的概念梁是一种常见的结构元素，广泛应用于建筑、桥梁、机械等领域。

在工程应用中，梁可以承受各种荷载导致的弯矩和剪力。

而梁的弯曲是指梁在承受荷载的作用下产生的曲率变化。

针对梁的弯曲问题，可以利用梁弯曲理论进行力学分析和结构设计。

梁弯曲的概念实际上涉及到两个重要的力学概念：弯矩和曲率。

弯矩是由外力作用在梁上产生的，它可以使梁产生弯曲或者使梁产生剪切变形。

曲率描述了梁的弯曲程度，是弯曲轴线的弯曲半径的倒数。

在分析梁弯曲时，通常会采用欧拉—伯努力学说，即假设梁在弯曲过程中，横截面平面仍然保持垂直于位移方向。

这个假设为了简化问题，但在一些特殊情况下可能需要引入其他理论模型。

梁弯曲的特点是在横向距离上产生剪切力和弯矩。

在梁的底部表面上，由于负弯矩的存在，会产生压应力；在梁的顶部表面上，由于正弯矩的存在，会产生拉应力。

而在距离横截面中性轴较远的位置，弯矩和曲率的值较大；而在中性轴附近位置，弯矩和曲率的值较小。

对于简单支承的梁，弯曲会导致两个基本的反应：梁曲率和梁挠度。

梁的曲率是横截面在垂直于曲线切线方向上的曲率半径的倒数。

梁的挠度是指梁在一点的纵向位移。

在分析梁弯曲时，可以利用弯曲方程和边界条件求解梁的曲率和挠度。

梁弯曲的分析可以应用不同的方法，其中最常用的方法是基于理想化梁的假设和采用弯曲方程。

对于简支梁，弯曲方程可以表示为：M = EI * d²y/dx²其中M是弯矩，E是弹性模量，I是截面惯性矩，y是梁的纵向位移，x是横向距离。

这个方程可以用来描述弯曲梁的受力和变形情况。

对于常见的梁形状，如矩形梁、T形梁或I形梁等，可以通过求解弯曲方程来得到梁的曲率和挠度分布。

这些分布信息可以用来评估梁的性能、设计合理的梁结构和验证结构的可靠性。

此外，在实际工程中，还需要考虑梁的极限弯矩和极限弯矩系数。

极限弯矩是指在不发生塑性滞后的情况下，梁能够承受的最大弯矩。

而极限弯矩系数是指实际弯矩与极限弯矩之间的比值。

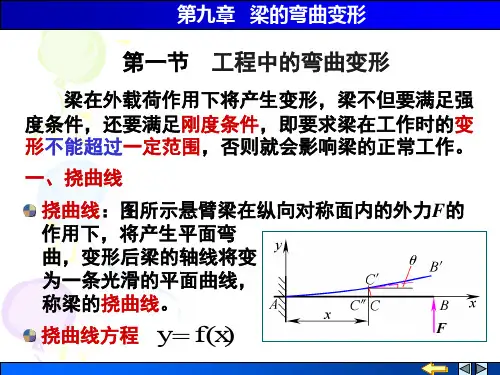
第7章-梁的弯曲变形(总32页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第7章 梁的弯曲变形与刚度梁弯曲变形的基本概念7.1.1 挠度在线弹性小变形条件下，梁在横力作用时将产生平面弯曲，则梁轴线由原来的直线变为纵向对称面内的一条平面曲线，很明显，该曲线是连续的光滑的曲线，这条曲线称为梁的挠曲线（图7-2）。

梁轴线上某点在梁变形后沿竖直方向的位移（横向位移）称为该点的挠度。

在小变形情况下，梁轴线上各点在梁变形后沿轴线方向的位移（水平位移）可以证明是横向位移的高阶小量，因而可以忽略不计。

挠曲线的曲线方程：)(x w w = （7-1）称为挠曲线方程或挠度函数。

实际上就是轴线上各点的挠度，一般情况下规定：挠度沿y 轴的正向（向上）为正，沿y 轴的负向（向下）为负（图7-4）。

必须注意，梁的坐标系的选取可以是任意的，即坐标原点可以放在梁轴线的任意地方，另外，由于梁的挠度函数往往在梁中是分段函数，因此，梁的坐标系可采用整体坐标也可采用局部坐标。

7.1.2 转角梁变形后其横截面在纵向对称面内相对于原有位置转动的角度称为转角（图7-3）。

转角随梁轴线变化的函数：)(x θθ= （7-2）称为转角方程或转角函数。

图7-3 梁的转角)(x 图7-2梁的挠曲线由图7-3可以看出，转角实质上就是挠曲线的切线与梁的轴线坐标轴x 的正方向之间的夹角。

所以有：xx w d )(d tan =θ,由于梁的变形是小变形，则梁的挠度和转角都很小，所以θ和θtan 是同阶小量，即：θθtan ≈，于是有：xx w x d )(d )(=θ （7-3） 即转角函数等于挠度函数对x 的一阶导数。

一般情况下规定：转角逆时针转动时为正，而顺时针转动时为负（图7-4）。

需要注意，转角函数和挠度函数必须在相同的坐标系下描述，由式（7-3）可知，如果挠度函数在梁中是分段函数，则转角函数亦是分段数目相同的分段函数。

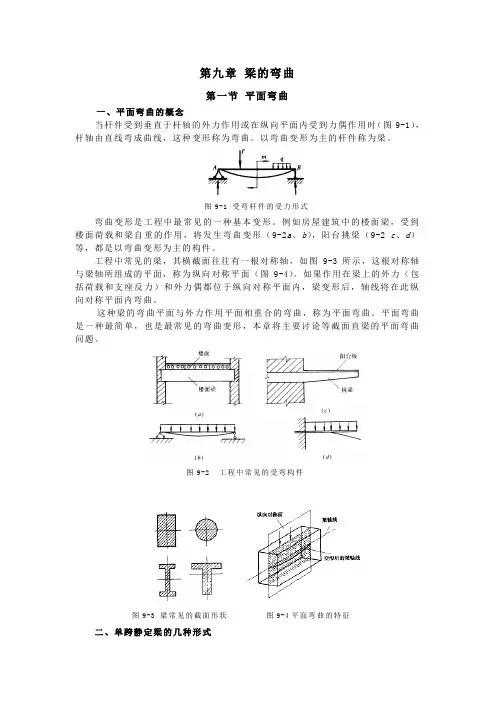
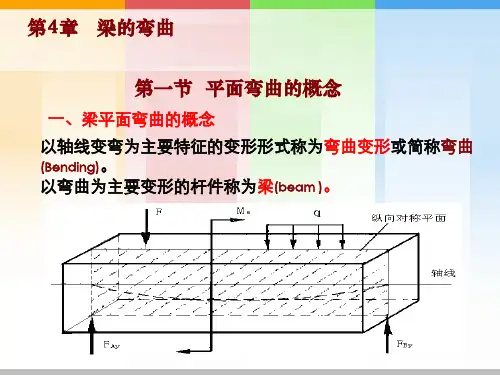
第九章梁的弯曲第一节平面弯曲一、平面弯曲的概念当杆件受到垂直于杆轴的外力作用或在纵向平面内受到力偶作用时（图9-1），杆轴由直线弯成曲线，这种变形称为弯曲。

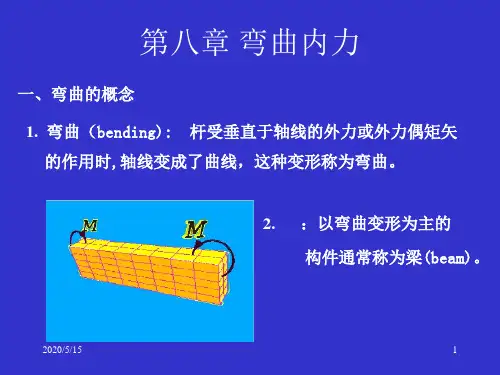
以弯曲变形为主的杆件称为梁。

图9-1 受弯杆件的受力形式弯曲变形是工程中最常见的一种基本变形。

例如房屋建筑中的楼面梁，受到楼面荷载和梁自重的作用，将发生弯曲变形（9-2a、b），阳台挑梁（9-2 c、d）等，都是以弯曲变形为主的构件。

工程中常见的梁，其横截面往往有一根对称轴，如图9-3所示，这根对称轴与梁轴所组成的平面，称为纵向对称平面（图9-4）。

如果作用在梁上的外力（包括荷载和支座反力）和外力偶都位于纵向对称平面内，梁变形后，轴线将在此纵向对称平面内弯曲。

这种梁的弯曲平面与外力作用平面相重合的弯曲，称为平面弯曲。

平面弯曲是一种最简单，也是最常见的弯曲变形，本章将主要讨论等截面直梁的平面弯曲问题。

图9-2 工程中常见的受弯构件图9-3 梁常见的截面形状图9-4平面弯曲的特征二、单跨静定梁的几种形式工程中对于单跨静定梁按其支座情况分为下列三种形式：1．悬臂梁： 梁的一端为固定端，另一端为自由端（图9-5a ）。

2．简支梁： 梁的一端为固定铰支座，另一端为可动铰支座（图9-5b ）。

3．外伸梁： 梁的一端或两端伸出支座的简支梁（图9-5c ）。

(a ) (b ) (c )图9-5 三种静定梁第二节 梁的弯曲内力——剪力和弯矩为了计算梁的强度和刚度问题，在求得梁的支座反力后，就必须计算梁的内力。

下面将着重讨论梁的内力的计算方法。

一、截面法求内力1、剪力和弯矩图9-6 用截面法求梁的内力图9-6a 所示为一简支梁，荷截F 和支座反力R A 、R B 是作用在梁的纵向对称平面内的平衡力系。

现用截面法分析任一截面m-m 上的内力。

假想将梁沿m-m 截面分为两段，现取左段为研究对象，从图9-6b 可见，因有座支反力R A 作用，为使左段满足Σ Y ＝０，截面m-m 上必然有与R A 等值、平行且反向的内力Q 存在，这个内力Q ，称为剪力；同时，因R A 对截面m-m 的形心O 点有一个力矩R A · a 的作用，为满足Σ M o ＝０，截面m-m 上也必然有一个与力矩R A · a 大小相等且转向相反的内力偶矩Ｍ存在，这个内力偶矩M 称为弯矩。

弯曲的定义：承受的外力作用线垂直于杆轴线。

在这种外力作用下，杆轴线由直线变为曲线。

这种变形称之为弯曲。

平面弯曲：梁变形后的轴线变成一条在纵向对称面内的平面直线，这类弯曲称之为平面弯曲。

按照支撑情况可以把梁分为悬臂梁、简支梁、外伸梁三种。

内力的计算一、内力方程：内力与截面位置坐标（x ）间的函数关系式。

Q=Q （x ）————剪力方程 M=M （x ）————弯矩方程 方法：截面法xY M m la l P Y Q Y A C A⋅=∴=-==∴=∑∑ , 0)( , 0PalAB1. 弯矩：M构件受弯时，横截面上其作用面垂直于截面的内力偶矩。

2. 剪力：Q构件受弯时，横截面上其作用线平行于截面的内力。

二、剪力图与弯矩图 1、求出支座反力2、写出剪力与弯矩的内力方程（含x 的方程）3、将写出的内力方程整理成含x 的已知函数关系，取特殊点描点连线即可。

（端点，与x 、y 轴的坐标点）弯曲构件横截面上的（内力）应力 1、弯矩M ———正应力σz I My=σ（弯曲正应力计算公式）maxZ Z y I W =(Wz —截面的抗弯截面系数) z t W M =max ,σ几种常见截面的 Iz 和 Wz 园截面： 644z d I π=323z d W π=空心截面： )1(6444z απ-=D I )1(3243z απ-=D W矩形截面： 123z bh I = 62z bh W =空心矩形截面： 12123300z bh h b I -= )2//()1212(03300z h bh h b W -=关于正应力的强度校核：① 校核强度： [m a xσ≤zW M② 设计截面尺寸：[m a xσM W z ≥③ 计算许可载荷：[max σz W M ≤2、剪力Q ——剪应力t*=zzbI QS 1τ其中Q 为截面剪力；S z 为y 点以下的面积对中性轴之静矩 Iz 为整个截面对z 轴之惯性矩；b 为y 点处截面宽度。

梁弯曲知识点总结一、弯曲概念在物理学和工程力学中，弯曲是指在材料受到外力作用下，产生一种曲率变化的变形形式。

在梁的情况下，当梁受到外部载荷作用时，梁将发生一种曲率变化，即梁的一部分受到压力而另一部分受到拉力，使得梁产生一种弯曲的变形形式。

梁的弯曲是梁理论研究的重要内容之一。

二、弯曲的原理梁的弯曲原理是由梁的弯矩和弯曲应力来描述的。

梁在弯曲时，横截面上的各个点受到的弯矩不同，由于弯矩的不平衡，在梁的上表面产生的张力，下表面产生的压力，产生了一种称为弯曲应力的内力形式。

弯曲应力的作用下，梁在弯曲的过程中产生了曲率变化，弯曲原理是用来描述梁在弯曲时的变形和内力情况的。

三、梁的弯曲方程梁的弯曲方程是用来描述梁在弯曲时的曲率和弯矩之间的关系的。

梁的弯曲方程可以通过力学原理和材料力学原理来推导出来。

梁的弯曲方程可以用来计算梁在受载时的弯曲变形和各个截面上的应力情况，对于工程结构的设计和分析具有非常重要的意义。

梁的弯曲方程通常包括以下几个方面：1.梁的弯曲变形方程：描述梁在弯曲时产生的曲率变化和曲线形状；2.梁的弯矩方程：描述梁在受力状况下产生的弯矩大小和分布情况；3.梁的弯曲应力方程：描述梁在弯曲状况下产生的应力大小和分布情况。

梁的弯曲方程是梁理论的核心内容，对于工程结构的设计和分析具有重要的意义。

四、梁的弯曲理论梁的弯曲理论是研究梁在受载时的弯曲变形和内力情况的理论。

梁的弯曲理论是以弹性理论和材料力学为基础的，通过对梁在弯曲时的力学原理和材料力学原理进行分析和推导，得出了梁在弯曲时的各种数学模型。

梁的弯曲理论可以应用于工程结构的设计和分析中，能够比较准确地描述梁在受载时的变形和内力情况，为工程结构的安全和稳定性提供理论依据。

梁的弯曲理论包括以下几个方面：1.梁的弯曲变形分析：描述梁在受载时产生的形状和曲率变化；2.梁的弯曲应力分析：描述梁在受载时产生的应力大小和分布情况；3.梁的弯曲挠度分析：描述梁在受载时产生的挠度大小和分布情况；4.梁的弯曲裂缝分析：描述梁在受载时产生的裂缝情况。

梁的弯曲概念梁的弯曲概念是指材料在作用力下发生弯曲变形的现象。

梁是一种常见的结构元素，广泛应用于建筑、机械、航空航天等领域。

在实际工程中，梁往往承受各种外部载荷，如重力、风载荷、地震载荷等。

因此，了解梁的弯曲行为对于结构设计和分析非常重要。

梁的弯曲行为可以通过经典的梁理论来描述。

经典梁理论假设梁是细长且直线的，在其轴向上受到均匀分布的轴向力和转矩，而其弯曲刚度足够大，可以忽略在轴向变形产生的内力，通过简化的数学模型来分析梁的弯曲行为。

在这种理论下，梁的弯曲变形可以用弯曲挠度和曲率来描述。

弯曲挠度是指梁在弯曲过程中沿截面上某一点的位移。

根据梁的弯曲方向和弯曲曲率的不同，可以分为正弯曲和负弯曲。

在梁的中性轴上，弯曲曲率为零，挠度最大。

根据梁的不同截面形状和外载荷的不同，梁的弯曲挠度可以用不同的数学表达式来计算。

曲率是指梁在弯曲过程中的曲率半径的倒数。

曲率反映了梁曲线的弯曲程度，曲率越大，梁的弯曲程度越大。

根据经典梁理论，梁的曲率与横截面的二阶惯性矩之比成正比。

对于不同形状和材料的截面，其曲率特性也有所不同。

在梁的弯曲过程中，材料内部产生了一系列力和应变。

根据材料力学理论，梁的弯曲行为可以用应变-应力关系来描述。

在弯曲曲率较小的情况下，弯曲应变可以通过材料的线弹性理论来描述。

根据胡克定律，弯曲应变与弯曲曲率成正比，弯曲应力与弯曲挠度成正比。

这种线性关系被称为小形变理论。

然而，在某些情况下，梁的弯曲程度较大，线弹性假设不再成立。

这时，需要考虑材料的非线性行为，如屈服、塑性变形和蠕变等。

这就需要使用非线性理论来描述梁的弯曲行为。

梁的弯曲行为对于结构设计和分析非常重要。

首先，了解梁的弯曲特性有助于确定合适的梁截面形状和材料。

其次，可以通过对梁的弯曲行为进行分析，评估梁的结构安全性和承载能力。

最后，可以根据梁的弯曲行为来制定适合的施工、保养和维护方案，以延长梁的使用寿命。

综上所述，梁的弯曲概念和行为在结构工程中占据重要地位。