梁的弯曲应力和强度问题

梁弯曲正应力实验中遇到的问题和解决方法
梁弯曲正应力实验是一种常见的力学实验，用于研究材料在受弯曲负载时的应力分布情况。

在进行这种实验时，有可能会遇到一些问题，下面是一些常见问题及其解决方法：
1. 梁的变形较大：当梁弯曲变形较大时，可能会导致实验结果不准确。

这可能是由于使用的材料强度不够或梁的截面形状不合适所引起的。

解决方法可以是使用更强度更高的材料或调整梁的截面形状以增加刚度。

2. 不均匀的载荷分布：在实验中，均匀的载荷分布对于获得准确的应力分布至关重要。

然而，由于实际操作中的误差或载荷施加不均匀，可能会导致载荷分布不均。

为了解决这个问题，可以使用适当的装置来均匀施加载荷，例如调整载荷点的位置或使用辅助支撑装置。

3. 测量误差：在实验测量过程中，可能会存在测量误差，例如测量长度或载荷的误差。

为了减小测量误差，可以使用更精确的测量仪器，例如数字测量仪或压力传感器，并进行多次重复测量以取得平均值。

4. 材料非线性行为：某些材料在受到较大应力时可能会出现非线性行为，例如弹性极限的超越或塑性变形。

这可能会影响到实验结果的准确性。

在这种情况下，可以选择更适合材料特性的实验方法，或者
进行更详细的材料力学性质测试。

5. 温度变化：温度的变化可能会导致材料的线膨胀或收缩，从而影响实验结果。

为了解决这个问题，可以进行温度补偿，即在实验过程中测量和控制温度变化，并根据材料的热膨胀系数进行修正。

总之，梁弯曲正应力实验是一种常见且有用的实验，但在实验过程中可能会遇到各种问题。

通过合适的措施和方法，可以克服这些问题，并获得准确可靠的实验结果。

提高梁弯曲强度的主要措施弯曲正应力是控制抗弯强度的主要因素。

因此，讨论提高梁抗弯强度的措施，应以弯曲正应力强度条件为主要依据。

由]σ[σmax max ≤=zW M 可以看出，为了提高梁的强度，可以从以下三方面考虑。

(1) 合理安排梁的支座和载荷从正应力强度条件可以看出，在抗弯截面模量z W 不变的情况下，M max 越小，梁的承载能力越高。

因此，应合理地安排梁的支承及加载方式，以降低最大弯矩值。

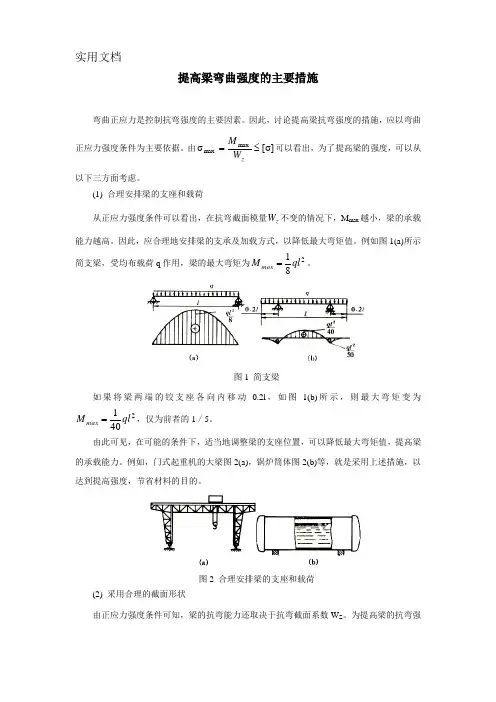
例如图1(a)所示简支梁，受均布载荷q 作用，梁的最大弯矩为281ql M max =。

图1 简支梁如果将梁两端的铰支座各向内移动0.2l ，如图1(b)所示，则最大弯矩变为2401ql M max =，仅为前者的1／5。

由此可见，在可能的条件下，适当地调整梁的支座位置，可以降低最大弯矩值，提高梁的承载能力。

例如，门式起重机的大梁图2(a)，锅炉筒体图2(b)等，就是采用上述措施，以达到提高强度，节省材料的目的。

图2 合理安排梁的支座和载荷(2) 采用合理的截面形状由正应力强度条件可知，梁的抗弯能力还取决于抗弯截面系数W Z 。

为提高梁的抗弯强度，应找到一个合理的截面以达到既提高强度，又节省材料的目的。

比值A W z 可作为衡量截面是否合理的尺度，AW z 值越大，截面越趋于合理。

例如图3中所示的尺寸及材料完全相同的两个矩形截面悬臂梁，由于安放位置不同，抗弯能力也不同。

竖放时662h bh bh A W z == 平放时 662b bh hb A W z == 当h>b 时，竖放时的A W z 大于平放时的AW z ，因此，矩形截面梁竖放比平放更为合理。

在房屋建筑中，矩形截面梁几乎都是竖放的，道理就在于此。

图3矩形梁的不同放置在讨论截面的合理形状时，还应考虑材料的特性。

对于抗拉和抗压强度相等的材料，如各种钢材，宜采用对称于中性轴的截面，如圆形、矩形和工字形等。

这种横截面上、下边缘最大拉应力和最大压应力数值相同，可同时达到许用应力值。

梁的应力和强度计算1.梁的基本假设梁的基本假设包括：梁材料是均匀各向同性的，梁截面是平面截面，梁的纵向伸缩变形可以忽略，梁的横向收缩变形可以忽略，梁截面平面保持平直。

2.梁的受力分析在进行梁的应力和强度计算之前，需要对梁的受力进行分析。

常见的梁的受力包括弯曲、剪切和轴向拉压等。

2.1弯曲弯曲是梁的一种主要受力状态，发生在梁受到弯矩作用时。

对于弯曲受力的梁，可以运用梁弯曲理论进行应力和强度计算。

常见的梁弯曲理论包括欧拉-伯努利梁理论和延性梁理论。

2.2剪切剪切是梁的另一种重要受力状态，发生在梁上部分截面受到剪力作用时。

剪切力引起梁截面上的剪应力，可以通过剪切变形理论进行计算。

2.3轴向拉压轴向拉压发生在梁上部分截面受到轴向拉力或压力作用时。

轴向拉力或压力引起梁截面上的轴向应力，可以通过轴向变形理论进行计算。

3.梁的应力分析根据梁的基本假设和受力分析，可以进行梁的应力分析。

梁的应力分析包括黄金区和非黄金区的判断、应力分布的计算和强度设计的确定。

3.1黄金区和非黄金区判断黄金区是指梁截面上应力最大的区域，通常位于材料的纤维处。

在黄金区内，应力达到梁材料的屈服强度。

非黄金区则是指其他区域，应力小于屈服强度。

3.2应力分布计算根据梁的受力和应力分析，可以计算出梁截面上的应力分布。

应力分布的计算可以通过梁的几何形状、外力和边界条件以及材料的性质来确定。

常见的应力分布包括弯曲应力、剪切应力和轴向应力等。

4.梁的强度设计梁的强度设计是根据计算得到的应力分布进行的。

根据材料的强度，可以确定梁的尺寸和形状，以满足梁的极限状态和使用状态的要求。

总结起来，梁的应力和强度计算是梁力学中的基本问题，包括梁的受力分析、应力分布计算和强度设计等内容。

通过合理的计算和设计，可以确保梁的安全和可靠性，提高结构的性能。

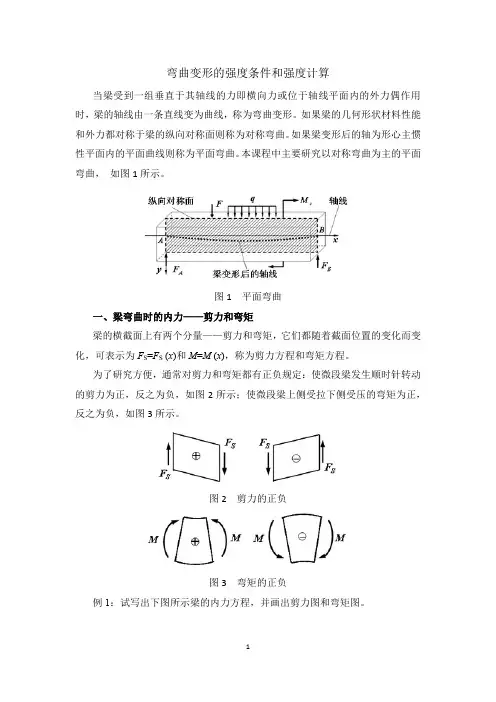
弯曲变形的强度条件和强度计算当梁受到一组垂直于其轴线的力即横向力或位于轴线平面内的外力偶作用时，梁的轴线由一条直线变为曲线，称为弯曲变形。

如果梁的几何形状材料性能和外力都对称于梁的纵向对称面则称为对称弯曲。

如果梁变形后的轴为形心主惯性平面内的平面曲线则称为平面弯曲。

本课程中主要研究以对称弯曲为主的平面弯曲，如图1所示。

图1 平面弯曲一、梁弯曲时的内力——剪力和弯矩梁的横截面上有两个分量——剪力和弯矩，它们都随着截面位置的变化而变化，可表示为F S=F S(x)和M=M (x)，称为剪力方程和弯矩方程。

为了研究方便，通常对剪力和弯矩都有正负规定：使微段梁发生顺时针转动的剪力为正，反之为负，如图2所示；使微段梁上侧受拉下侧受压的弯矩为正，反之为负，如图3所示。

图2 剪力的正负图3 弯矩的正负例1：试写出下图所示梁的内力方程，并画出剪力图和弯矩图。

解：（1）求支反力=∑C M：0310126=⨯--⋅AyF，kN7=AyF=∑Y：010=-+ByAyFF，kN3=ByF（2）列内力方程剪力：⎩⎨⎧<<-<<=63kN33kN7)(S xxxF弯矩：⎩⎨⎧≤≤≤≤⋅-⋅-=633mkN)6(3mkN127)(xxxxxM（3）作剪力图和弯矩图二、梁弯曲时的正应力在一般情况下，梁的横截面上既有弯矩又有剪力。

若梁上只有弯矩没有剪力，称为纯弯曲。

本讲主要讨论纯弯曲时横截面上的应力——正应力。

梁横截面上的正应力大小与该点至中性轴的距离成正比，即正应力沿截面宽度均匀分布，沿高度呈线性分布，如图4所示。

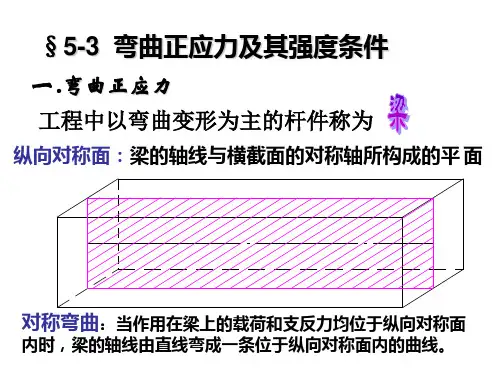
图4 梁弯曲时的正应力分布图即有yIxMz)(=σ（1）中性轴把截面分成受拉区和受压区两部分，且最大拉应力和最大压应力发生在上下边缘处，其值为max max y I Mz=σ。

令max y I W z z=，即有：zW M =max σ （2）式中，W z 称为抗弯截面系数，它与横截面的几何尺寸和形状有关，量纲为[长度]3，常用单位为mm 3或m 3。

梁的应力及强度计算梁是一种常见的结构元件，用于承受或分配荷载。

在设计和分析梁的过程中，计算梁的应力及强度是非常重要的。

本文将详细介绍梁的应力及强度计算方法。

首先，梁的应力定义为单位面积上的力，用公式表示为：σ=M*y/I其中，σ表示梁的应力，M表示梁的弯矩，y表示距离中性轴的垂直距离，I表示梁的截面惯性矩。

梁的应力通常包括弯曲应力、剪切应力和轴向应力。

弯曲应力是由于弯曲力引起的应力，计算公式为：σ_b=M*y/I其中，σ_b表示弯曲应力。

剪切应力是由于纵向剪力引起的应力，计算公式为：τ=V*Q/(b*t)其中，τ表示剪切应力，V表示纵向剪力，Q为形状系数，b为梁的宽度，t为梁的厚度。

轴向应力是由于轴向力引起的应力，计算公式为：σ_a=N/A其中，σ_a表示轴向应力，N表示轴向力，A表示梁的截面积。

梁的强度是指在给定的荷载下梁能够承受的最大应力。

在计算梁的强度时，通常需要将不同种类的应力进行合并。

弯曲强度是指梁在弯曲荷载下的抗弯矩能力。

根据材料的弯曲性能和形状，可以采用破坏理论或变形理论计算梁的弯曲强度。

剪切强度是指梁在剪切荷载下的抗剪切能力。

根据材料的剪切性能和梁的几何形状，可以计算出梁的剪切强度。

轴向强度是指梁在轴向荷载下的抗轴向力能力。

轴向强度的计算通常基于材料的抗拉性能。

在进行梁的应力及强度计算时，还需要考虑其他因素，如材料的弹性模量、断裂韧性和安全系数等。

总之，梁的应力及强度计算是结构设计和分析中必不可少的一部分。

通过合理的计算方法，可以确保梁在荷载下的正常工作和安全使用。

《机械设计基础》课程单元教学设计单元标题：梁弯曲时横截面上的应力及强度计算单元教学学时 2在整体设计中的位置第16次授课班级上课地点教学目标能力目标知识目标素质目标能利用强度计算条件进行承载能力计算1．掌握应力计算公式2．掌握强度计算条件1.培养学生热爱本专业、爱学、会学的思想意识。

2.培养学生应用理论知识分析和解决实际问题的能力；3.培养学生的团队合作意识；4.培养学生仔细、认真、严谨的工作态度。

能力训练任务及案例任务：能利用强度计算条件进行承载能力计算教学材料1.教材2.使用多媒体辅助教学单元教学进度步骤教学内容教学方法学生活动工具手段时间分配1复习、导入复习总结：弯曲变形截面上剪力和弯矩的求法，剪力图、弯矩图的绘图步骤。

导入：梁弯曲时横截面上的应力及强度计算。

提问讲授讨论回答黑板课件视频5分钟2设置情景提出问题简支矩形截面木梁如图所示，L=5m,承受均布载荷q=3.6kN/m，木材顺纹许用应力［σ］＝10MPa，梁截面的高宽比h/b=2，试选择梁的截面尺寸。

问题探究问题引领听讲思考黑板、ppt5分钟一.纯弯曲概念：１.纯弯曲：平面弯曲中如果某梁段剪力为零，该梁段称为纯弯曲梁段。

２.剪切弯曲：平面弯曲中如果某梁段剪力不为零（存在剪力），该梁段称为剪切弯曲梁段。

二.纯弯曲时梁的正应力：1.中性层和中性轴的概念：中性层：纯弯曲时梁的纤维层有的变长，有的变短。

其中有一层既不伸长也不缩短，这一层称为中性层。

中性轴：中性层与横截面的交线称为中性轴。

10分钟3讲授新知提供咨询２.纯弯曲时梁的正应力的分布规律：以中性轴为分界线分为拉区和压区，正弯矩上压下拉，负弯矩下压上拉，正应力成线性规律分布，最大的正应力发生在上下边沿点。

３、纯弯曲时梁的正应力的计算公式：（１）.任一点正应力的计算公式：（２）.最大正应力的计算公式：其中：M---截面上的弯矩；I Z---截面对中性轴(z轴)的惯性矩； y---所求应力的点到中性轴的距离。

混凝土梁的弯曲强度标准一、引言混凝土梁是建筑结构中常用的构件之一，其承担着承重、支撑等多种功能。

在使用过程中，混凝土梁的弯曲强度是一个至关重要的指标。

因此，制定混凝土梁的弯曲强度标准对于确保建筑结构的安全和可靠是非常重要的。

二、弯曲强度的定义弯曲强度是指混凝土梁在受到弯曲作用时所能承受的最大应力。

一般用弯矩和截面惯性矩的比值来表示，即：f_b = M / I其中，f_b为弯曲应力，M为弯矩，I为截面惯性矩。

三、影响弯曲强度的因素1.混凝土的强度：混凝土的强度越高，其弯曲强度也相应提高。

2.钢筋的配筋率：钢筋的配筋率越高，混凝土梁的弯曲强度也相应提高。

3.截面形状：不同形状的截面对混凝土梁的弯曲强度有不同的影响。

4.荷载的大小和作用方式：不同大小和作用方式的荷载对混凝土梁的弯曲强度有不同的影响。

5.梁跨度：梁跨度越大，混凝土梁的弯曲强度越低。

四、弯曲强度标准为了确保混凝土梁的安全可靠，制定弯曲强度标准是非常必要的。

以下是常见的两种弯曲强度标准：1.中国建筑标准设计规范《混凝土结构设计规范》(GB 50010-2010)该标准规定了不同等级混凝土梁的弯曲强度等级，如下表所示：等级 | f_b(MPa)---|---C15 | 2.5C20 | 2.8C25 | 3.1C30 | 3.4C35 | 3.7C40 | 4.0C45 | 4.2C50 | 4.4C55 | 4.6C60 | 4.82.美国混凝土协会《建筑规范》(ACI 318-14)该标准将混凝土梁的弯曲强度按等级划分为A、B、C、D四个等级，如下表所示：等级 | f_b(MPa)---|---A | 7.5B | 10C | 12.5D | 15五、弯曲强度的检验方法为了检验混凝土梁的弯曲强度是否符合标准要求，需要进行相应的测试。

常见的测试方法有以下两种：1.三点弯曲试验该试验方法是将混凝土梁放置在两个支点上，施加作用于中央的负载，测量混凝土梁在受力时的弯曲程度，从而计算出其弯曲强度。

第六章 弯曲应力和强度1、 纯弯曲时的正应力 横力弯曲时，0≠=Q dxdM。

，纯弯曲时，梁的横截面上只有弯曲正应力，没有弯曲剪应力。

根据上述实验观察到的纯弯曲的变形现象，经过判断、综合和推理，可作出如下假设： （1）梁的横截面在纯弯曲变形后仍保持为平面，并垂直于梁弯曲后的轴线。

横截面只是绕其面内的某一轴线刚性地转了一个角度。

这就是弯曲变形的平面假设。

（2）梁的纵向纤维间无挤压，只是发生了简单的轴向拉伸或压缩。

（2）物理关系根据梁的纵向纤维间无挤压，而只是发生简单拉伸或压缩的假设。

当横截面上的正应力不超过材料的比例极限P ρ时，可由虎克定律得到横截面上坐标为y 处各点的正应力为y EE ρεσ==该式表明，横截面上各点的正应力σ与点的坐标y 成正比，由于截面上ρE为常数，说明弯曲正应力沿截面高度按线性规律分布，如图所示。

中性轴z 上各点的正应力均为零，中 性轴上部横截面的各点均为压应力，而下部各点则均为拉应力。

（3）静力关系截面上的最大正应力为zI My maxmax =σ 如引入符号m axy I W zz =则截面上最大弯曲正应力可以表达为zW M=max σ 式中，z W 称为截面图形的抗截面模量。

它只与截面图形的几何性质有关，其量纲为[]3长度。

矩形截面和圆截面的抗弯截面模量分别为： 高为h ，宽为b 的矩形截面：621223maxbh h bh y I W zz ===直径为d 的圆截面：3226433maxd d d y I W z z ∏=∏==至于各种型钢的抗弯截面模量，可从附录Ⅱ的型钢表中查找。

若梁的横截面对中性轴不对称，则其截面上的最大拉应力和最大压应力并不相等，例如T 形截面。

这时，应把1y 和2y 分别代入正应力公式，计算截面上的最大正应力。

最大拉应力为：zt I My 1)(=σ 最大压应力为：ze I My 2)(=σ 2、横力弯曲时的正应力zI My=σ 对横力弯曲时的细长梁，可以用纯弯曲时梁横截面上的正应力计算公式计算梁的横截面上的弯曲正应力。