梁正截面受弯承载力配筋计算(公式编制的Excel表格)(精)

混凝土工字形抗弯承载力 excel混凝土工字形梁是一种常见的结构构件，具有很好的抗弯承载能力。

在工程设计中，确定混凝土工字形梁的抗弯承载力是非常重要的一项工作。

本文将详细介绍混凝土工字形梁的抗弯承载力计算方法，并通过Excel表格的方式进行展示。

一、混凝土工字形梁的抗弯承载力计算公式混凝土工字形梁的抗弯承载力可以通过以下公式计算得出：M = f * b * h^2 / 6其中，M为混凝土工字形梁的抗弯弯矩，f为混凝土的抗弯强度，b 为梁的宽度，h为梁的高度。

二、混凝土工字形梁的抗弯承载力计算实例假设某工程需要设计一根混凝土工字形梁，其宽度为0.3米，高度为0.6米，混凝土的抗弯强度为25MPa。

我们可以通过上述公式计算该梁的抗弯承载力。

将以上数值代入公式中，可得：M = 25 * 0.3 * 0.6^2 / 6= 1.5 kNm三、混凝土工字形梁抗弯承载力计算表格为了更直观地展示混凝土工字形梁的抗弯承载力计算过程，我们可以使用Excel表格进行展示。

具体表格如下：| 宽度（m） | 高度（m） | 抗弯强度（MPa） | 抗弯承载力（kNm）||-----------|----------|-----------------|------------------|| 0.3 | 0.6 | 25 | 1.5 |通过这个表格，我们可以清晰地看到混凝土工字形梁的抗弯承载力计算结果。

四、混凝土工字形梁抗弯承载力的影响因素混凝土工字形梁的抗弯承载力受到多个因素的影响，包括混凝土的抗弯强度、梁的宽度和高度等。

其中，混凝土的抗弯强度是最重要的因素之一，其数值越大，梁的抗弯承载力也就越大。

而梁的宽度和高度则是通过几何关系来影响抗弯承载力的，宽度越大、高度越大，梁的抗弯承载力也就越大。

五、混凝土工字形梁的抗弯承载力设计要求在实际工程设计中，我们需要根据具体的使用要求和安全系数要求来确定混凝土工字形梁的抗弯承载力设计值。

正截面抗弯承载力计算公式弯曲方向上的抗弯矩可以通过以下公式计算：M=σ*y*S其中，M为弯矩，单位为N·mm；σ为截面的应力，单位为N/mm²；y为截面的离心距，即截面中心到受拉纤维的距离，单位为mm；S为截面的抵抗矩，单位为mm³。

剪切方向上的抗剪力可以通过以下公式计算：V=τ*A其中，V为剪力，单位为N；τ为截面中剪应力，单位为N/mm²；A为截面的剪切面积，单位为mm²。

综合考虑两种方向上的抗弯承载力，可以得到正截面抗弯承载力的计算公式：W = Min(M/b , V/yc)其中，W为正截面的抗弯承载力，单位为N；M为弯矩，单位为N·mm；b为截面的宽度，单位为mm；V为剪力，单位为N；yc为截面的离心距，即截面中心到受拉纤维的距离，单位为mm。

在实际设计中，为了保证结构的安全性，通常需要根据材料的强度参数和结构的要求来确定截面的尺寸和形状。

在正截面抗弯承载力的计算过程中，需要注意以下几个要点：1.材料的强度参数：计算前需要明确截面所采用的材料的强度参数，如屈服强度和抗拉强度等。

2.截面形状的选择：根据结构的要求和截面的受力条件，选择适当的截面形状，如矩形、圆形、梯形等。

3.弯矩和剪力的确定：根据结构的受力分析，确定截面上的弯矩和剪力大小。

4.抵抗矩和剪切面积的计算：根据截面形状的不同，采用相应的计算方法计算抵抗矩和剪切面积。

5.安全系数的考虑：为了保证结构的安全性，在计算过程中通常会引入相应的安全系数，以考虑不同因素对结构性能的影响。

总之，正截面抗弯承载力的计算需要考虑弯曲方向上的抗弯矩和剪切方向上的抗剪力，通过综合考虑两者，可以得到正截面的抗弯承载力的计算公式。

在使用公式进行计算时，需要明确材料的强度参数，选择适当的截面形状，并考虑安全系数的影响，以确保结构的安全性。

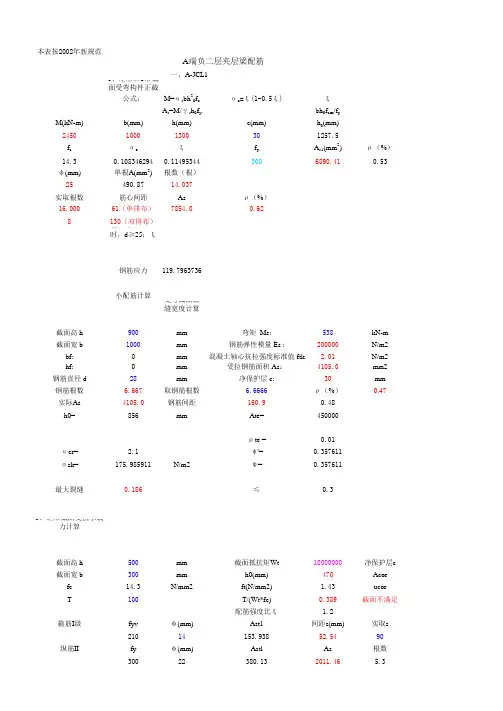
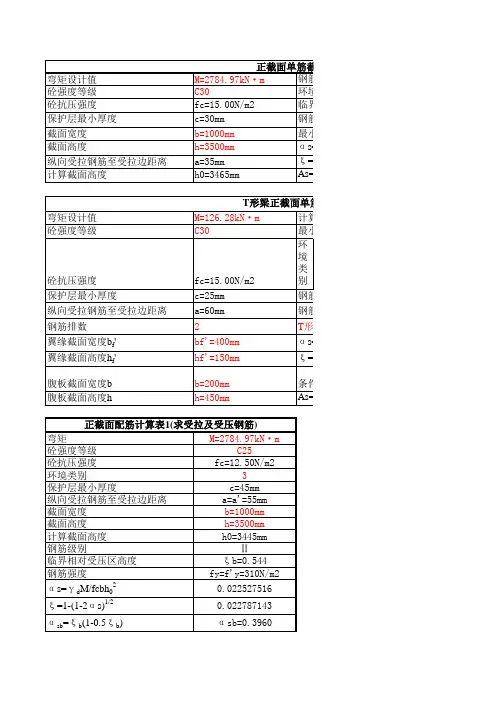
本表按2002年新规范A端负二层夹层梁配筋一、A-JCL11、矩形和T形截面受弯构件正截面受弯承载力计算公式：M=αs bh20f cαs=ξ(1-0.5ξ)γs=1-0.5ξA s=M/γs h0f y A s=ξb h0f cm/f yM(kN-m)b(mm)h(mm)c(mm)h0(mm)245010001300301257.5f cαsξf y A s1(mm2)ρ（%）14.30.1083462940.114953443006890.410.53φ(mm)单根A(mm2)根数（根）25490.8714.037实取根数筋心间距Asρ（%）16.00061（单排布）7854.00.628130（双排布）注：ξ≥0.544时，d≥25；ξ≥0.556时，d≠28~40。

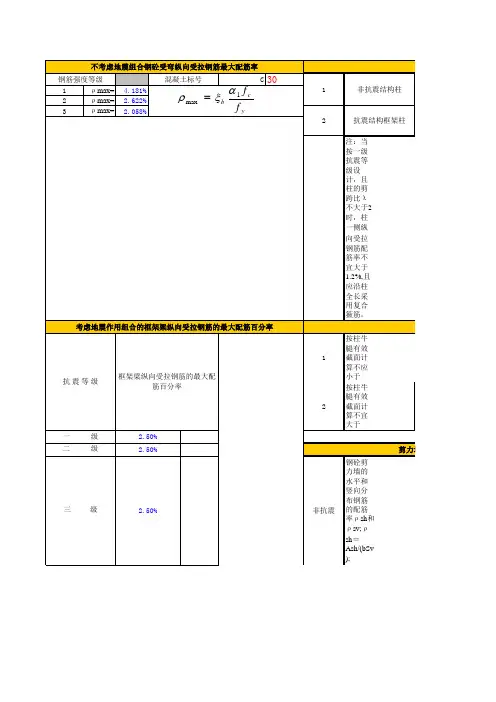
构件斜截面钢筋应力119.79637362、裂缝控制最小配筋计算受弯截面裂缝宽度计算截面高 h900mm弯矩 Ms:538kN-m截面宽 b1000mm钢筋弹性模量 Es :200000N/m2 bf:0mm混凝土轴心抗拉强度标准值 ftk 2.01N/m2hf:0mm受拉钢筋面积 As：4105.0mm2钢筋直径 d28mm净保护层 c:30mm钢筋根数 6.667取钢筋根数 6.6666ρ（%）0.47实际As4105.0钢筋间距160.90.48h0=856mm Ate=450000ρte =0.01αcr= 2.1ψ'=0.357611σsk=175.985911N/m2ψ=0.357611最大裂缝0.186≤0.33、矩形截面受扭承载力计算截面高 h500mm截面抵抗矩Wt18000000净保护层c截面宽 b300mm h0(mm)470Acor fc14.3N/mm2ft(N/mm2) 1.43ucorT100T/(Wt*fc)0.389截面不满足配筋强度比ξ 1.2箍筋I级fyvφ(mm)Ast1间距s(mm)实取s21014153.93852.5490纵筋II fyφ(mm)Astl As根数30022380.132011.46 5.3实取纵筋根数Asρ（%）ρtl,min（%）41520.53 1.078〉0.5454、深受弯构件正截面受弯承载力计算公式：α1f c bx=f y A SA s=M/zf y z=a d(h0-0.5x)a d=0.80+0.04l0/hM(kN-m)b(mm)h(mm)c(mm)h0(mm)a d0100090030856 1.22f cαsξf y A s(mm2)ρ（%）14.3003000.000.00φ(mm)单根A(mm2)根数（根）28615.750.000实取根数筋心间距Asρ（%）0.00000.00.0000注：ξ≥0.544时，d≥25；ξ≥0.556时，d≠28~40。

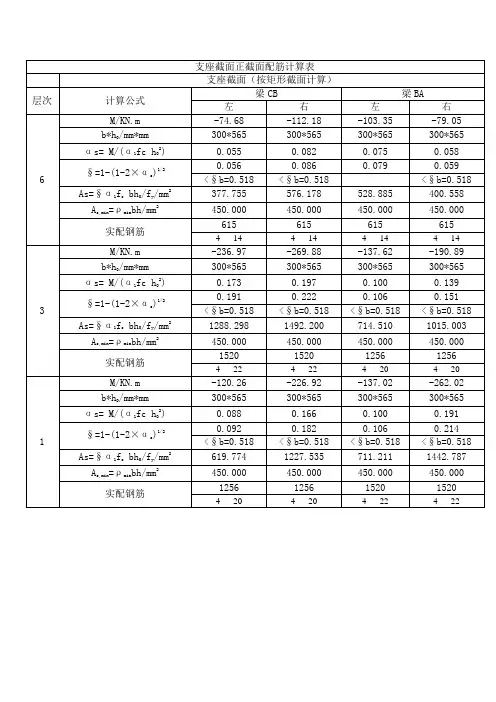
声明：
1。

本程序为上海同济大学2003级结构工程李凌志编制整理，目的说明：
1。

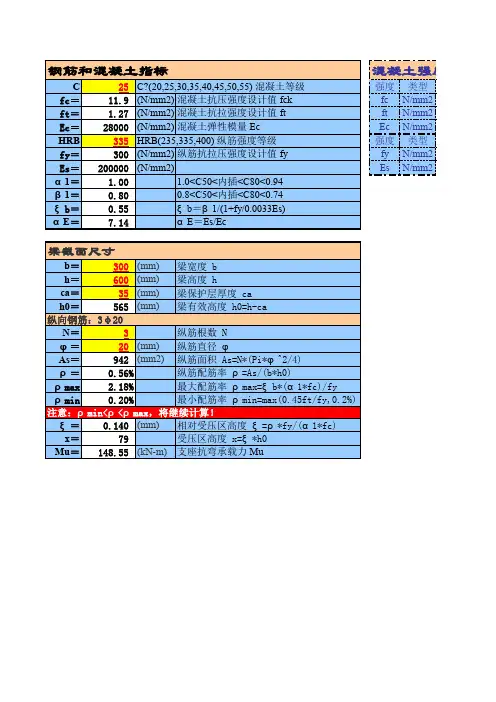
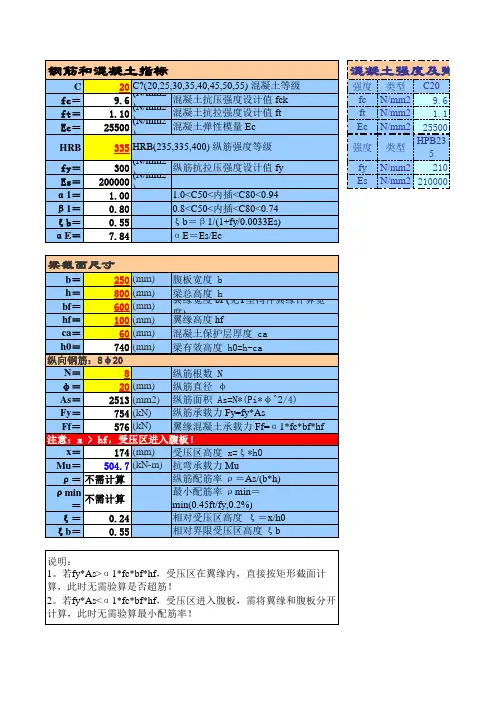
若fy*As>α1*fc*bf*hf ，受压区在翼缘内，直接按矩形截面计算，此时无需验算是否超筋！
2。

若fy*As<α1*fc*bf*hf ，受压区进入腹板，需将翼缘和腹板分开计算，此时无需验算最小配筋率！
1。

本程序为上海同济大学2003级结构工程李凌志编制整理，目的是为了便于在电脑上用Excel和在PDA上用Pocket Excel进行简单的结构手算，程序根据新规范编制，如有什么疑问请联系我，以便立刻修正！
2。

程序中黄底红字的部分需要使用者根据实际情况输入，黑色的部分请不要随便更改，除非你发现有错误！
email：lingzhi0512@
OICQ：49551484
如需获得更多Excel手算程序请登录 。

正截面抗弯承载力计算公式1.梁的弯矩-曲率等价受力法梁的弯矩-曲率等价受力法是一种简化计算正截面抗弯承载力的方法，其中最为常用的是Euler-Bernoulli梁理论。

其计算公式如下：M=σ×W=E×I×κ/c其中M为截面所受弯矩；σ为截面受压及受拉应力；W为截面模量；E为材料的弹性模量；I为截面的惯性矩；κ为截面弯曲时的曲率；c为截面的半径。

具体步骤为：1）根据实际情况，确定梁的材料和几何尺寸；2）计算截面的惯性矩I；3）根据外力作用下梁的曲线形状，计算截面的曲率κ；4）根据所需的安全系数和抗弯强度，确定截面的允许应力σ；5）根据公式计算截面的抗弯承载力。

2.截面法截面法是一种采用截面抗弯承载力的公式直接计算截面的抗弯能力。

根据杆件受力情况的不同，可分为梁受拉和受压两种情况。

梁受拉的计算公式为：N/A+M/W≤σc其中N为截面受拉的力；A为截面的面积；M为截面受弯矩；W为截面模量；σc为材料的抗压强度。

梁受压的计算公式为：N/A+M/W≤σt其中N为截面受压的力；A为截面的面积；M为截面受弯矩；W为截面模量；σt为材料的抗拉强度。

根据公式计算出截面受压或受拉状态下的几何形状，再根据所需的安全系数和抗弯强度，确定截面的允许应力σc或σt，最后得到截面的抗弯承载力。

3.模型法模型法是一种采用有限元数值计算方法来分析截面抗弯承载力的计算方法。

通过建立杆件的数学模型，利用有限元法进行数值分析，得到截面的应力分布及强度。

该方法较为精确，但计算复杂且耗时。

总结：正截面抗弯承载力的计算可以采用梁的弯矩-曲率等价受力法、截面法和模型法等方法。

这些计算公式一般都需要根据具体的材料、几何尺寸和外力情况进行调整，以满足工程的安全要求。

因此，在实际计算中，应根据具体情况选择适用的计算方法和公式来计算正截面抗弯承载力。

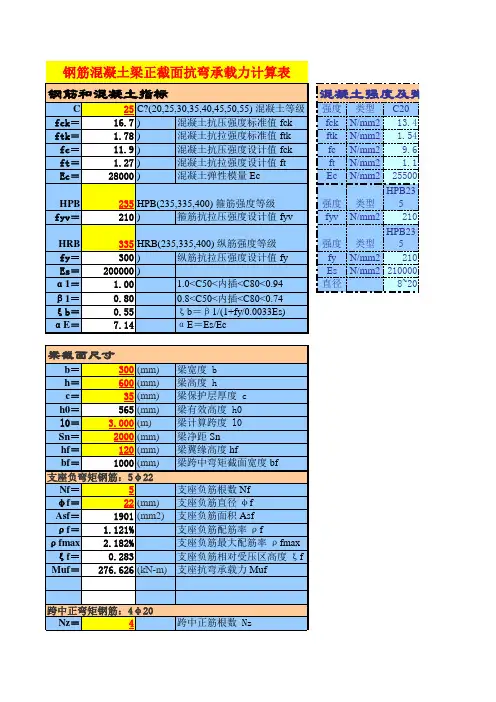
λ不1.2%,且应沿柱全长ρs为竖向、水平分布钢筋的0.20%; 2）框架－剪力墙0.4%1）钢筋砼梁中箍筋配筋率1) V>0.7f t bh 0ρsv ＝A sv /bs ≥0.24f t /f yv2) 在弯剪扭构件中，剪扭箍筋的配筋率ρsv ＝Asv/bs ≥0.28ft/fyv ，其中Asv 为配置在同一截面内具体见上表。

2) 梁内受扭纵向钢筋的配筋率柱钢bhA stl tl=rA stl ：沿截面周边布置的受扭纵向钢筋的总截面面积。

受拉纵向钢筋的配筋率不应小于其中，b 为矩形截面的宽度，或T 形截面的腹板宽受扭纵向受力钢筋的最小配筋百分率bhA stl tl=r yc f f Vb T 6.0等级设计，且柱的剪跨比λ不大于2时，柱一侧纵不宜大于1.2%,且应沿柱全长采用复合箍筋。

计算不应小于腿有效截面计算不宜大于和竖向分布钢筋的配筋率ρsh 和ρsv;ρsh ＝Ash/(bSv);sv/(bSh);Sh 、Sv 为竖向、水平分布钢筋的间距)≥0.2%。

重要部位的，其水平和竖向分布钢筋的配筋率宜适当提高、二、三级抗震等级的剪力墙的水平和竖向分布钢筋最小配筋率均不应小于0.25；小于0.20%; 2）框架－剪力墙结构中的水平和竖向分布钢筋最小配筋0.25%；3）部分框架－剪力墙结构的剪力墙底部加强部位的水平和竖向分布应小于0.4%5560657075800.6040.5940.5840.5750.5650.5550.5400.5310.5220.5120.5030.4930.5080.4990.4900.4810.4720.46225.3027.5029.7031.8033.8035.901.96 2.04 2.09 2.14 2.18 2.220.990.980.970.960.950.940.790.780.770.760.750.74，其中Asv 为配置在同一截面内箍筋各肢的全部截面面积。

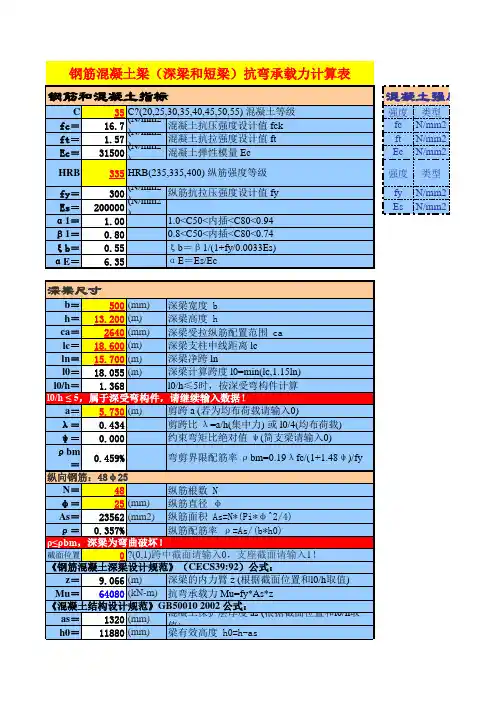
1.17931.09080.250.1890.3640.42980.3976
0.2
梁端一排钢筋数量超限
梁底底部钢筋根数是否超限
梁底部纵向钢筋的最小配筋率(%)梁端纵向受拉钢筋的配筋率(%)（按有效高度）梁端混凝土受压区高度和有效高度之比
梁端截面的底筋和顶面纵向钢筋配筋量的比值梁底部纵向钢筋的配筋率(%)（按有效高度）梁端纵向受拉钢筋的最小配筋率(%)梁底部纵向钢筋的配筋率(%)（按全截面）梁端上部钢筋根数是否超限梁端纵向受拉钢筋的配筋率(%)（按全截面） 说明：表中绿色单元格表示需要用户填写内容，黄色单元格表示计算结果，红字标示出需要注意的事项,另注意本表格不适用于4排及其以上钢筋的情况。

表中钢筋根数是否超限根
据输入不同钢筋根数和直
径计算是否一排满足，不满足需用户手动更改钢筋排数，这样计算得到的其它数据才正确。