承载力计算-抗弯-矩形截面-双筋excle计算公式

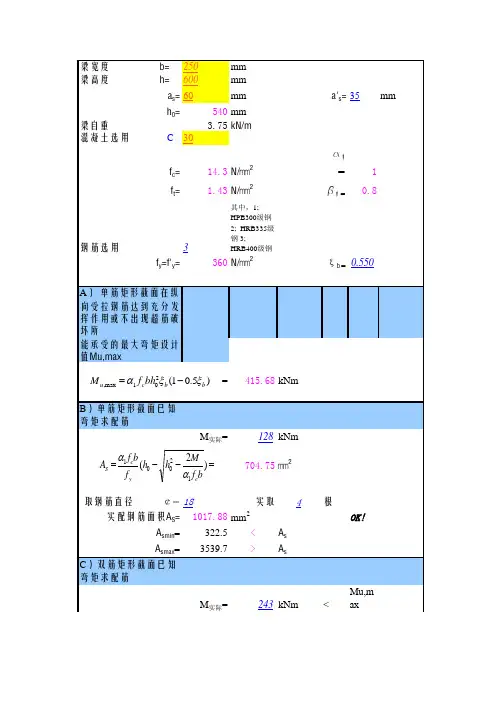
矩形截面偏心受压构件正截面的承载力计算一、矩形截面大偏心受压构件正截面的受压承载力计算公式 （一）大偏心受压构件正截面受压承载力计算（1）计算公式由力的平衡条件及各力对受拉钢筋合力点取矩的力矩平衡条件，可以得到下面两个基本计算公式：s y s y c A f A f bx f N -+=''1α （7-23）()'0''012a h A f x h bx f Ne s y c -+⎪⎭⎫ ⎝⎛-=α （7-24）式中： N —轴向力设计值；α1 —混凝土强度调整系数；e —轴向力作用点至受拉钢筋A S 合力点之间的距离；a he e i -+=2η （7-25） a i e e e +=0 （7-26）η—考虑二阶弯矩影响的轴向力偏心距增大系数，按式（7-22）计算；e i —初始偏心距；e 0 —轴向力对截面重心的偏心距，e 0 =M/N ；e a —附加偏心距，其值取偏心方向截面尺寸的1/30和20㎜中的较大者； x —受压区计算高度。

（2）适用条件1) 为了保证构件破坏时受拉区钢筋应力先达到屈服强度，要求b x x ≤ (7-27)式中 x b — 界限破坏时，受压区计算高度，o b b h x ξ= ，ξb 的计算见与受弯构件相同。

2) 为了保证构件破坏时，受压钢筋应力能达到屈服强度，和双筋受弯构件相同，要求满足：'2a x ≥ (7-28) 式中 a ′ — 纵向受压钢筋合力点至受压区边缘的距离。

（二）小偏心受压构件正截面受压承载力计算（1）计算公式根据力的平衡条件及力矩平衡条件可得s s s y c A A f bx f N σα-+=''1 （7-29）⎪⎭⎫ ⎝⎛'-+⎪⎭⎫ ⎝⎛-=s s y c a h A f x h bx f Ne 0''012α （7-30） ()'0''1'2s s s s c a h A a x bx f Ne -+⎪⎭⎫⎝⎛-=σα （7-31）式中 x — 受压区计算高度，当x ＞h ，在计算时，取x ＝h ；σs — 钢筋As 的应力值，可根据截面应变保持平面的假定计算，亦可近似取：y b s f 11βξβξσ--=(7-32)要求满足：y s y f f ≤≤σ'x b — 界限破坏时受压区计算高度，0h x b b ξ=；b ξξ、 — 分别为相对受压区计算高度 x/h 0和相对界限受压区计算高度x b /h 0 ；'e e 、′— 分别为轴向力作用点至受拉钢筋A s 合力点和受压钢筋A s ′合力点之间的距离 a he e i -+=2η (7-33) ''2a e he i --=η (7-34) （2）对于小偏心受压构件当bh f N c >时，除按上述式（7-30）和式（7-31）或式（7-32）计算外，还应满足下列条件：()()s s y c a a h A f h h bh f e e a h N -+⎪⎭⎫⎝⎛-≤⎥⎦⎤⎢⎣⎡---'0''00'22 (7-35 )式中 '0h — 钢筋's A 合力点至离纵向较远一侧边缘的距离，即s a h h -='0。

正截面抗弯承载力计算公式弯曲方向上的抗弯矩可以通过以下公式计算：M=σ*y*S其中，M为弯矩，单位为N·mm；σ为截面的应力，单位为N/mm²；y为截面的离心距，即截面中心到受拉纤维的距离，单位为mm；S为截面的抵抗矩，单位为mm³。

剪切方向上的抗剪力可以通过以下公式计算：V=τ*A其中，V为剪力，单位为N；τ为截面中剪应力，单位为N/mm²；A为截面的剪切面积，单位为mm²。

综合考虑两种方向上的抗弯承载力，可以得到正截面抗弯承载力的计算公式：W = Min(M/b , V/yc)其中，W为正截面的抗弯承载力，单位为N；M为弯矩，单位为N·mm；b为截面的宽度，单位为mm；V为剪力，单位为N；yc为截面的离心距，即截面中心到受拉纤维的距离，单位为mm。

在实际设计中，为了保证结构的安全性，通常需要根据材料的强度参数和结构的要求来确定截面的尺寸和形状。

在正截面抗弯承载力的计算过程中，需要注意以下几个要点：1.材料的强度参数：计算前需要明确截面所采用的材料的强度参数，如屈服强度和抗拉强度等。

2.截面形状的选择：根据结构的要求和截面的受力条件，选择适当的截面形状，如矩形、圆形、梯形等。

3.弯矩和剪力的确定：根据结构的受力分析，确定截面上的弯矩和剪力大小。

4.抵抗矩和剪切面积的计算：根据截面形状的不同，采用相应的计算方法计算抵抗矩和剪切面积。

5.安全系数的考虑：为了保证结构的安全性，在计算过程中通常会引入相应的安全系数，以考虑不同因素对结构性能的影响。

总之，正截面抗弯承载力的计算需要考虑弯曲方向上的抗弯矩和剪切方向上的抗剪力，通过综合考虑两者，可以得到正截面的抗弯承载力的计算公式。

在使用公式进行计算时，需要明确材料的强度参数，选择适当的截面形状，并考虑安全系数的影响，以确保结构的安全性。

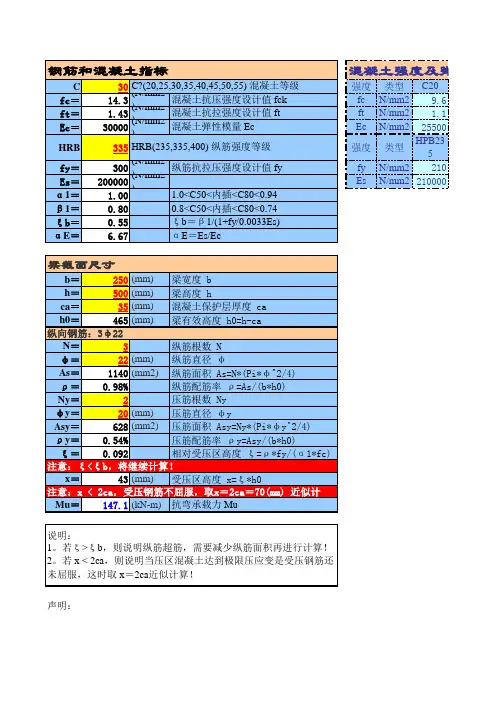
二、双筋矩形截面受弯构件正承载力计算（一）计算简图在进行双筋矩形截面受弯构件正截面承载力计算时，计算简图如图3-19所示。

（二）基本公式（1）设计表达式根据图3-19所示的计算简图和内力平衡条件，可列出基本设计计算公式()⎥⎦⎤⎢⎣⎡'-''+⎪⎭⎫ ⎝⎛-=≤a h A f x h bx f M M 0s y 0c d d u 21γγ （3-14） s y s y c A f A f bx f ''-= （3-15）为了计算方便，将0h x ξ=代入式(3-14)、式(3-15)，可得()[]a h A f bh f M M s s '-''+=≤0y 20c dd u 1αγγ （3-16） s y s y 0c A f A f h b f ''-=ξ （3-17） 式中 f y '——钢筋抗压强度设计值，按附录4表3取用；A's ——受压区纵向钢筋截面面积；a'——受压钢筋合力点至受压区边缘的距离。

（2）适用条件1）与单筋截面一样，为避免发生超筋情况，要求ξ≤ξb （3-18）2）保证受压钢筋应力能够达到抗压强度设计值，要求x ≥2a' （3-19）因为如果x 值太小，受压钢筋就太靠近中和轴，将得不到足够的变形，应力也就达不到抗压强度设计值，因而基本公式便不能成立。

双筋截面承受的弯矩较大，相应配置的受拉钢筋也较多，一般不必验算ρ≥ρmin 的条件。

（3）x ＜2a' 时的计算公式对于x ＜2a' 的情况，受压钢筋应力达不到f y '。

此时可近似假定受压钢筋的压力与受压混凝土的压力作用于同一直线上，且经过受压钢筋重心位置（图3-20）。

以受压钢筋合力点为力矩中心 ，可得()a h A f M M '-=≤0s y dd u 1γγ （3-20） 式(3-20)是双筋截面在x ＜2a' 时的唯一基本公式。

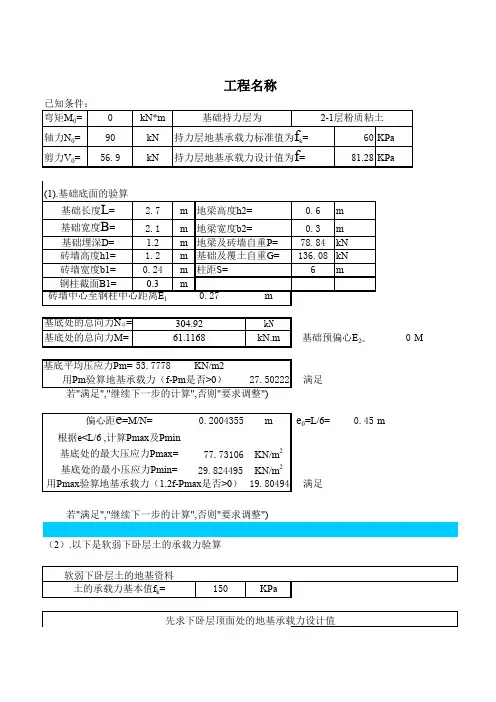
简 支 钢 梁 计 算基本数据输入:梁跨度： l=9000mm梁间距a=2400mm钢材：Q 345f =315N/mm 2fv =185N/mm 2 上翼缘：b 1=400mm t 1=14mm 下翼缘：b 2=300mm t 2=12mm 腹 板：h w =574mm t w =8mm即: 断面截面特性计算：钢梁截面：A 0=13792mm 2 重量108.3kg/m 钢梁中和轴的位置：y 0=342mm钢梁对X轴截面惯性矩：I z =8.94E+08mm4钢梁上翼缘的弹性抵抗矩：W 1x = 3.46E+06mm 3 钢梁下翼缘的弹性抵抗矩：W 2x = 2.61E+06mm 3 钢梁对Y轴截面惯性矩：I y = 1.02E+08mm 4i y =85.9 mm y =104.8上翼缘对Y 轴的惯性矩：I 1=7.47E+07mm 4下翼缘对Y 轴的惯性矩：I 2= 2.70E+07mm 40.73 截面不对称影响系数：0.380.53 工字形截面简支梁的系数0.76 梁的整体稳定系数：0.74 修正后：0.672.截面验算：（1）弯矩及剪力的计算：=+=211I I I b α=-=)12(8.0b b αη=bβ==hb t l 111ξ=bφ='bφλ钢梁自重： 1.30KN/m恒载： 4.00KN/m2g1k=10.90KN/m活载：q c= 3.0KN/m2p k=18.10KN/m p=23.16KN/m 弯矩：M=234.49KN·m剪力：V=104.22KN（2）钢梁的强度、稳定和挠度的验算：梁的整体稳定应力：σ=101.01N/mm2钢梁上翼缘应力：σ1=67.70N/mm2钢梁下翼缘应力：σ2=89.68N/mm2钢梁剪应力：τ=22.70N/mm2挠度：w=8.4mmw/l=1/1072。

一.1b=100t=10h=230s=6B=200T=104380mm2152mm98mm 4.6E+07mm 4302773mm 3469607mm 32混凝土等级C208.08板厚h d100梁跨度6000梁左相邻净距1800梁右相邻净距1800板托顶宽b 0300板托高度h t150b 1 =600b 2 =6001500mm150000mm 222944.4mm 2402mm混凝土板顶面至组合截面中和轴的距离 x= [b e *h d 2/(2*αE )+A*y]/A 0 =117mm混凝土截面惯性矩 I c = b e *h d 3/12=1.3E+08mm4换算成钢截面的组合截面惯性矩 I 0 = I c /αE + A c *(x-0.5h d )2/αE + I + A(y-x)2 =5E+08mm 43.5E+07mm 42.4E+08mm 43763855mm 41307031mm 4313662.2mm 2混凝土板顶面至组合截面中和轴的距离x c = [b e *h d 2/(4*αE )+A*y]/A 0c=162mm4.2E+08mm 44.2E+07mm 41.1E+08mm 44800913mm 41249942mm 4二施工阶段的验算1弯矩和剪力钢梁自重：0.41kN/m 板自重： 6.00kN/m 2000mm)板托重：0.90kN/m 6.09kN/m 自重标准值 g 1：7.31kN/m施工荷载： 2.80kN/m 施工阶段弯矩设计值M 45.51kN.m (梁跨度：6000mm)施工阶段剪力设计值V 30.34kN2钢梁抗弯强度设计143.14N/mm 2<215N/mm 2PASS!92.29N/mm2<215N/mm2PASS!3钢梁剪应力计算面积矩 S=207492mm 322.80N/mm 2<125N/mm 2PASS!4挠度计算考虑混凝土徐变的组合截面特征计算换算成钢截面的组合截面面积 A 0c = A c / 2αE + A =换算成钢截面的组合截面惯性矩 I 0c = I c /(2*αE ) + A c *(x c -0.5h d )2/(2*αE) + I + A(y-x c )2 =(平台梁间距：对混凝土板底面的组合截面弹性抵抗矩 w 0c b =αE *I 0 / (x - h d ) =对钢梁上翼缘的组合截面弹性抵抗矩 w 0t = I 0 / (d-x) =对混凝土板顶面的组合截面弹性抵抗矩 w 0c tc = 2αE *I 0c / x c =对钢梁下翼缘的组合截面弹性抵抗矩 w 0b = I 0 / (H-x) =组合梁计算截面特征计算钢梁面积 A ＝b*t + h*s +B*T =钢梁中和轴至钢梁顶面的距离为 y t = [0.5b*t 2 + h*s*(0.5h + t) + B*T*(t+h+0.5T)] / A =钢梁截面特征计算：钢梁截面惯性矩 I= (b*t 3+ s*h 3+ B*T 3) / 12 + b*t*(yt-0.5t)2+ s*h*(y t -0.5h-t)2 + B*T*(0.5T+h+t-y t )2 =钢梁中和轴至钢梁顶面的距离为 y b = h + t + T - y t =钢梁上翼缘的弹性抵抗矩 W 1 = I / y t =混凝土板顶面至钢梁截面中和轴的距离 y = h d + h t +y t =对混凝土板顶面的组合截面弹性抵抗矩 w 0c t = αE *I 0 / x=混凝土板计算宽度b e =钢梁上翼缘的弹性抵抗矩 W 2 = I / y b =组合截面特征计算：钢与混凝土弹性模量比αE =混凝土板截面面积A c = b e * h d =换算成钢截面的组合截面面积A 0=A c /αE +A =自重标准值 g 1k ：对混凝土板底面的组合截面弹性抵抗矩 w 0c bc =2αE *I 0c / (x c - h d ) =对钢梁上翼缘的组合截面弹性抵抗矩 w 0tc = I 0c / (d-x c ) =对钢梁下翼缘的组合截面弹性抵抗矩 w 0bc = I 0c / (H-x c ) =钢梁上翼缘应力 M / r x *W 1 =钢梁下翼缘应力 M / r x *W 2 =钢梁剪应力τ1max = v 1*s 1/I*t w =△=5*g*l 4/(384*E*I)=10.8mm < L/400 =15mm PASS!三使用阶段的验算1弯矩及剪力找平层重： 1.9kN/m 活荷载：15.6kN/m （活荷载：6kn/m 2)78.84kN.m 52.56kN22.1-2.28N/mm 2<10N/mm 2PASS!-0.33N/mm2<10N/mm2PASS!-87.74N/mm 2<215N/mm 2PASS!130.39N/mm2<215N/mm2PASS!2.2-2.24N/mm 2<10N/mm 2PASS!-0.37N/mm 2<10N/mm 2PASS!-88.23N/mm 2<215N/mm 2PASS!130.69N/mm 2<215N/mm 2PASS!2.3(略）2.4(略)3钢梁的剪应力147000mm 31105812mm 319.35N/mm 2<125N/mm 2PASS!4组合梁的挠度3.46mm < L/400 =15mm PASS!△＝5q k l 4/384EI o +5g k l 4/384EI o c =组合梁中由于混凝土收缩引起的内力钢梁腹板顶面处对钢梁中和轴的面积矩S 1=钢梁腹板顶面以外的砼及钢梁上翼缘对组合截面中和轴的面积矩S o =τ＝V 1S 1/It w +V 2S o /I o T w =两个受力阶段的荷载对组合梁的钢梁产生的剪应力使用阶段弯矩设计值M 使用阶段剪力设计值V 考虑混凝土徐变在垂直荷载作用下的正应力混凝土板顶面应力:σ0c tc =-(M 2g /W 0c tc +M 2q /W 0c t )=组合梁的抗弯强度在垂直荷载作用下的正应力混凝土板顶面应力σ0c t =-M/W 0c t =混凝土板底面应力σ0c b =-M/W 0c b =钢梁上翼缘应力σ0t= -M 1/W 1+M 2/W 0t=钢梁下翼缘应力σ0b= -M 1/W 2+M 2/W 0b=σ0bc = -M 1/W 2+(M 2g /W 0bc +M 2q /W 0b )=钢梁下翼缘应力温度差产生的应力σ0c bc =-(M 2g /W 0c bc +M 2q /W 0c b )=混凝土板底面应力:钢梁上翼缘应力σ0tc = -M 1/W 1+(M 2g /W 0tc +M 2q /W 0t )=。