3.1组合逻辑电路的基本分析方法

《组合逻辑电路》教案一、教学目标1. 理解组合逻辑电路的基本概念和原理。

2. 掌握组合逻辑电路的分析和设计方法。

3. 能够运用组合逻辑电路解决实际问题。

二、教学内容1. 组合逻辑电路的基本概念：什么是组合逻辑电路，组合逻辑电路的特点。

2. 组合逻辑电路的原理：组合逻辑电路的构成，组合逻辑电路的工作原理。

3. 组合逻辑电路的分析方法：组合逻辑电路的分析步骤，如何判断组合逻辑电路的功能。

4. 组合逻辑电路的设计方法：组合逻辑电路的设计步骤，如何选择适当的逻辑门实现组合逻辑电路。

5. 组合逻辑电路的应用：组合逻辑电路在实际中的应用案例，如何利用组合逻辑电路解决问题。

三、教学方法1. 讲授法：讲解组合逻辑电路的基本概念、原理和分析方法。

2. 案例分析法：分析组合逻辑电路的实际应用案例，让学生更好地理解组合逻辑电路的应用。

3. 实践操作法：让学生通过实际操作，设计组合逻辑电路，提高学生的实际动手能力。

四、教学准备1. 教学PPT：制作组合逻辑电路的教学PPT，用于辅助讲解和展示。

2. 教学案例：准备一些组合逻辑电路的实际应用案例，用于分析。

3. 实验器材：准备一些逻辑门电路元件，让学生进行实践操作。

五、教学过程1. 导入：通过简单的逻辑门电路实例，引入组合逻辑电路的概念。

2. 讲解：讲解组合逻辑电路的基本概念、原理和分析方法。

3. 分析：分析一些组合逻辑电路的实际应用案例，让学生理解组合逻辑电路的应用。

4. 设计：让学生分组设计一些组合逻辑电路，并进行展示和讲解。

5. 总结：总结本节课的重点内容，布置课后作业。

六、教学评估1. 课堂问答：通过提问方式检查学生对组合逻辑电路基本概念的理解程度。

3. 设计作业：评估学生设计的组合逻辑电路方案，检查其分析和实现能力。

七、教学难点与解决策略1. 组合逻辑电路的复杂性：通过实例分析和简化方法，帮助学生理解复杂的组合逻辑电路。

2. 设计方法的灵活运用：引导学生运用创造性思维，灵活运用设计方法。

组合逻辑电路的分析在分析组合逻辑电路时，我们可以使用真值表、卡诺图或布尔代数等方法。

下面将分别介绍这些方法的基本原理和应用。

1.真值表分析法真值表是列出电路的所有可能输入和对应输出的表格。

通过逐行检查真值表的输出列，可以确定电路的功能。

真值表分析法适用于较小规模的电路，但对于较复杂的电路可能不够实用。

2.卡诺图分析法卡诺图是一种图形表示方法，用于描述逻辑函数之间的关系。

它将所有可能的输入组合表示为一个方格矩阵，每个方格代表一个状态。

相邻的方格表示输入之间只有一个位不同。

通过合并相邻的方格，我们可以找到简化逻辑函数的最小项或最小项组合。

卡诺图分析法可以用来优化逻辑电路，减少门的数量和延迟。

3.布尔代数分析法布尔代数是一种用符号和运算规则描述逻辑函数的代数系统。

我们可以使用布尔代数的运算规则来简化和优化逻辑电路。

常见的布尔代数运算包括与运算、或运算、非运算和异或运算等。

通过应用这些运算规则，我们可以将复杂的逻辑函数简化为最小项或最小项组合，从而简化电路。

在进行组合逻辑电路的分析时，我们首先需要确定电路的输入和输出。

然后，我们可以根据电路的功能和输出要求，绘制真值表或卡诺图。

通过分析真值表或卡诺图，我们可以找到逻辑函数的最小项或最小项组合。

接下来，我们可以将这些最小项或最小项组合转化为逻辑门的输入方式。

最后，我们可以使用布尔代数的运算规则来简化逻辑函数和电路。

组合逻辑电路的分析是电路设计和优化的重要一步。

通过应用不同的分析方法，我们可以更好地理解电路的功能和性质，从而更好地设计和优化电路。

在分析组合逻辑电路时，我们需要注意电路的输入和输出要求，合理选择和配置逻辑门，以及优化电路的延迟和开销。

组合逻辑电路的分析与设计方法一、教学目标：组合逻辑电路的分析方法、组合逻辑电路的设计方法二、教学重点、难点：重点掌握组合逻辑电路的分析步骤、组合逻辑电路的设计步骤三、教学过程设计：1.定义：任意时刻的输出状态只决定于该时刻的输入状态，而与从前的状态无关。

2.组合逻辑电路的分析步骤：1)由逻辑图写出各输出端的逻辑表达式；2)化简和变换各逻辑表达式；3)列出真值表；4)根据真值表和逻辑表达式对逻辑电路进行分析，最后确定其功能。

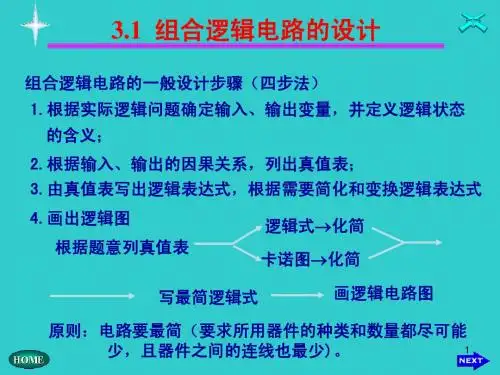
3.组合逻辑电路的设计步骤：1)根据实际逻辑问题确定输入、输出变量，并定义逻辑状态的含义；2)根据输入、输出的因果关系，列出真值表；3)由真值表写出逻辑表达式，根据需要简化和变换逻辑表达式；4)画出逻辑图；讲完后讲解个例题：试用与非门和反相器设计一个优先排队电路。

火车有特快、直快和慢车。

它们进出站的优先次序是：特快、直快、慢车，同一时刻只能有一列车进解：1) 由题意进行逻辑抽象。

当特快A=1时，无论直快B，慢车C 为何值，LA=1，LB= LC=0；当直快B=1，且A= 0 时，无论C为何值，LB=1，LA =LC=0；当慢车C=1，且A=B=0 时，LC=1，LA= LB=0。

经过逻辑抽象，可列真值表：2)写出逻辑表达式：3) 画出逻辑电路图：让学生计算几个练习题，加深理解，时间如果允许可以让学生到黑板上来做四、课后作业：1、已知逻辑电路如图所示，分析该电路的功能。

解：1）根据逻辑图，写出输出逻辑表达式L⊕ZC=CA⊕B=)(⊕BA⊕C=⊕2）列写真值表3）确定逻辑功能：电路具有为奇校验功能五、本节小结：对本节内容进行小结。

第三章组合逻辑电路基本知识点*组合逻辑电路的特点*组合逻辑电路功能的表示方法及相互转换*组合逻辑电路的分析方法和设计方法*常用集成组合逻辑电路的逻辑功能、使用方法和应用举例*组合逻辑电路中的竞争–冒险现象及消除竞争–冒险现象的常用方法3.1概述在数字电路中根据逻辑功能的不同特点，可将其分为两大类：一类是组合逻辑电路，另一类是时序逻辑电路。

组合逻辑电路在逻辑功能上的共同特点是：任意时刻的输出状态仅取决于该时刻的输入状态，与电路原来的状态无关。

在电路结构上的特点是：它是由各种门电路组成的，而且只有从输入到输出的通路，没有从输出到输入的反馈回路。

由于组合逻辑电路的输出状态与电路的原来状态无关，所以组合逻辑电路是一种无记忆功能的电路。

由此可知第二章中介绍的各种门电路都属于组合逻辑电路。

描述一个组合逻辑电路逻辑功能的方法很多，通常有：逻辑函数表达式、真值表、逻辑图、卡诺图、波形图五种。

它们各有特点，又相互联系，还可以相互转换。

3. 2逻辑功能各种表示方法的特点及其相互转换一、逻辑功能各种表示方法的特点1、逻辑函数表达式逻辑表达式是用与、或、非等基本运算来表示输入变量和输出函数因果关系的逻辑代数式。

其特点是形式简单、书写方便，便于进行运算和转换。

但表达式形式不唯一。

2、真值表真值表是根据给定的逻辑问题，把输入变量的各种取值的组合和对应的输出函数值排列成表格。

其特点是：直观、明了，可直接看出输入变量与输出函数各种取值之间的一一对应关系。

真值表具有唯一性。

3、逻辑图逻辑图是用若干基本逻辑符号连接成的电路图。

其特点是：与实际使用的器件有着对应关系，比较接近于实际的电路，但它只反映电路的逻辑功能而不反映电气参数和性能。

同一种逻辑功能可以用多种逻辑图实现，它不具备唯一性。

4、卡诺图卡诺图是按相邻性原则排列的最小项的方格图。

它实际上是真值表的特定的图示形式。

其特点是在化简逻辑函数时比较直观容易掌握。

卡诺图具有唯一性，但化简后的逻辑表达式不是唯一的。

第3章组合逻辑电路3.1 组合逻辑电路的概述按照逻辑功能的不同特点，可以把数字电路分成两大类，一类叫做组合逻辑电路，另一类叫做时序逻辑电路。

什么叫组合逻辑电路呢？在t=a时刻有输入X1、X2、……Zn，那么在t=a时刻就有输出Z1、Z2、……Zm，每个输出都是输入X1、X2、……Zn的函数，Z1=f1（X1、X2、……Xn）Z1=f2（X1、X2、……Xn）Zm=fm（X1、X2、……Xn）从以上概念可以知道组合逻辑电路的特点就是即刻输入，即刻输出。

任何组合逻辑电路可由表达式、真值表、逻辑图和卡诺图等四种方法中的任一种来表示其逻辑功能。

3.2 组合逻辑电路的分析方法和设计方法3.2.1组合逻辑电路的分析方法分析组合逻辑电路的目的，就是要找出电路输入和输出之间的逻辑关系，分析步骤如下：（1）根据已知的逻辑电路，写出逻辑函数表达式（采用逐级写出逻辑函数表达式），最后写出该电路的输出与输入的逻辑表达式。

（2）首先对写出的逻辑函数表达式进行化简，一般系用公式法或卡诺图法。

（3）列出真值表进行逻辑功能的分析。

以上步骤可用框图表示，如图3-2所示。

图3-2 组合逻辑电路分析框图下面举例说明对组合逻辑电路的分析，掌握其基本思路及方法。

【例3-1】 分析图3-3所示电路的逻辑功能图3-3 [例3-1]逻辑电路解：（1）写出输出Z 的逻辑表达式： Z1=B A ， Z2=B AZ=21Z Z •=B A B A • （2）化简Z=B A B A •=A B +A B=A ⊕B （3）列出真值表进行逻辑功能说明 列出该函数真值表，如表3.1所示： 表3-1 [例3-1]真值表 A B Z 0 0 0 0 1 1 1 0 1 1 13.2.2组合逻辑电路的设计方法组合逻辑电路的设计步骤与分析步骤相反，设计任务就是根据逻辑功能的要求设计逻辑电路，其步骤如下：（1）首先对命题要求的逻辑功能进行分析，确定哪些是输入变量，哪些为输出函数，以及它们之间的相互逻辑关系，并对它们进行逻辑赋值。

第三章组合逻辑电路基本要求：熟练掌握组合逻辑电路的分析方法；掌握组合逻辑电路的设计方法；理解全加器、译码器、编码器、数据选择器、数据比较器的概念和功能，并掌握它们的分析与实现方法；了解组合逻辑电路中的险象本章主要内容：组合逻辑电路的分析方法和设计方法。

本章重点：组合逻辑电路的分析方法组合逻辑电路的设计方法常用逻辑部件的功能本章难点：组合逻辑电路的设计一、组合逻辑电路的特点若一个逻辑电路，在任一时刻的输出仅取决于该时刻输入变量取值组合，而与电路以前的状态无关，则电路称为组合逻辑电路（简称组合电路）。

可用一组逻辑函数描述。

组合电路根据输出变量分为单输出组合逻辑电路和多输出组合逻辑电路。

注意：1.电路中不存在输出端到输入端的反馈通路。

2.电路不包含记忆元件。

3.电路的输出状态只由输入状态决定。

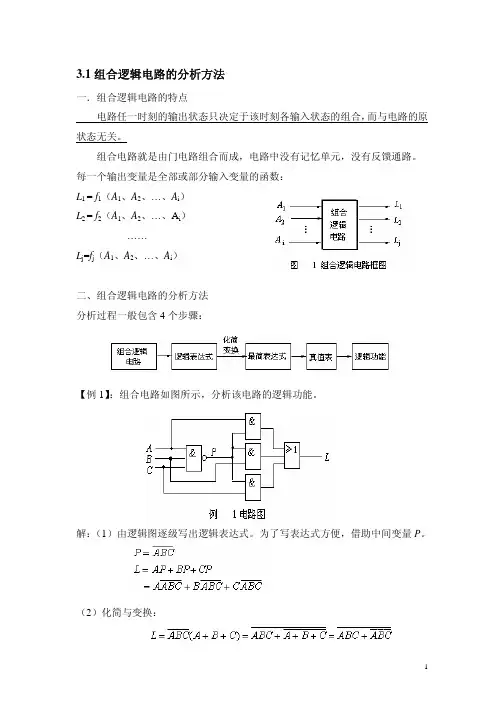
二、组合逻辑电路的分析方法分析的含义：给出一个组合逻辑电路，分析它的逻辑功能。

分析的步骤: 1.根据给出的逻辑电路图，逐级推导，得到输出变量相对于输入变量的逻辑函数。

2.对逻辑函数化简。

3.由逻辑函数列出对应的真值表。

4.由真值表判断组合电路的逻辑功能。

三、组合电路的分析举例１、试分析图3-1所示的单输出组合逻辑电路的功能解：（1）由G1、G2、G3各个门电路的输入输出关系，推出整个电路的表达式：Z1=ABCF=Z1+Z2 （2）对该逻辑表达式进行化简：（3）根据化简后的函数表达式，列出真值表3-1。

（4）从真值表中可以看出：当A、B、C三个输入一致时（或者全为“0”、或者全为“1”），输出才为“1”，否则输出为“0”。

所以，这个组合逻辑电路具有检测“输入不一致”的功能，也称为“不一致电路”。

２.试分析图3－2所示的输出组合逻辑电路的功能解：（1）由G1、G2、G3、G4、G5各个门电路的输入、输出关系，推出整个组合逻辑电路的表达式：（2)对该逻辑表达式进行化简：（3）根据化简后的函数表达式，列出真值表3-2。

（4）若设A、B各为一位二进制加数，则从真值表中可以看出，S为两加数相加后的一位和、C为两加数相加后的进位值。