二次函数与相似专题复习

专题29二次函数与相似、全等存在性问题题型一相似三角形存在性问题在坐标系中确定点，使得由该点及其他点构成的三角形与其他三角形相似，即为“相似三角形存在性问题”．【相似判定】判定1：三边对应成比例的两个三角形是相似三角形；判定2：两边对应成比例且夹角相等的两个三角形是相似三角形；判定3：有两组角对应相等的三角形是相似三角形．以上也是坐标系中相似三角形存在性问题的方法来源，根据题目给的已知条件选择恰当的判定方法，解决问题【题型分析】通常相似的两三角形有一个是已知的，而另一三角形中有1或2个动点，即可分为“单动点”类、“双动点”两类问题．【思路总结】根据相似三角形的做题经验，可以发现，判定1基本是不会用的，这里也一样不怎么用，对比判定2、3可以发现，都有角相等！所以，要证相似的两个三角形必然有相等角，关键点也是先找到一组相等角．然后再找：思路1：两相等角的两边对应成比例；思路2：还存在另一组角相等．事实上，坐标系中在已知点的情况下，线段长度比角的大小更容易表示，因此选择方法可优先考虑思路1．一、如何得到相等角？二、如何构造两边成比例或者得到第二组角？搞定这两个问题就可以了．1．如图，在平面直角坐标系中，抛物线C：y＝ax2+bx+c（a≠0）经过点（1，1）和（4，1）．（1）求抛物线C的对称轴．（2）当a＝﹣1时，将抛物线C向左平移2个单位，再向下平移1个单位，得到抛物线C1．①求抛物线C1的解析式．②设抛物线C1与x轴交于A，B两点（点A在点B的右侧），与y轴交于点C，连接BC．点D为第一象限内抛物线C1上一动点，过点D作DE⊥OA于点E．设点D的横坐标为m．是否存在点D，使得以点O，D，E为顶点的三角形与△BOC相似？若存在，求出m的值；若不存在，请说明理由．2．如图，抛物线y＝ax2+bx+3（a≠0）与x轴交于点A（1，0）和点B（﹣3，0），与y轴交于点C，连接BC，与抛物线的对称轴交于点E，顶点为点D．（1）求抛物线的解析式；（2）点P是对称轴左侧抛物线上的一个动点，点Q在射线ED上，若以点P、Q、E为顶点的三角形与△BOC 相似，请直接写出点P的坐标．3．如图，直线y＝﹣x+分别交x轴、y轴于点A，B，过点A的抛物线y＝﹣x2+bx+c与x轴的另一交点为C，与y轴交于点D（0，3），抛物线的对称轴l交AD于点E，连接OE交AB于点F．（1）求抛物线的解析式；（2）求证：OE⊥AB；（3）P为抛物线上的一动点，直线PO交AD于点M，是否存在这样的点P，使以A，O，M为顶点的三角形与△ACD相似？若存在，求点P的横坐标；若不存在，请说明理由．4．如图，在平面直角坐标系xOy中，抛物线y＝﹣x2+x+4与两坐标轴分别相交于A，B，C三点．（1）求证：∠ACB＝90°；（2）点D是第一象限内该抛物线上的动点，过点D作x轴的垂线交BC于点E，交x轴于点F，点G是AC 的中点，若以点C，D，E为顶点的三角形与△AOG相似，求点D的坐标．5．如图，已知二次函数的图象与x轴交于A和B（﹣3，0）两点，与y轴交于C（0，﹣3），对称轴为直线x＝﹣1，直线y＝﹣2x+m经过点A，且与y轴交于点D，与抛物线交于点E，与对称轴交于点F．（1）求抛物线的解析式和m的值；（2）在y轴上是否存在点P，使得以D、E、P为顶点的三角形与△AOD相似，若存在，求出点P的坐标；若不存在，试说明理由；题型二全等三角形存在性问题6．如图，抛物线y＝x2+bx+c经过点（3，12）和（﹣2，﹣3），与两坐标轴的交点分别为A，B，C，它的对称轴为直线l．（1）求该抛物线的表达式；（2）P是该抛物线上的点，过点P作l的垂线，垂足为D，E是l上的点．要使以P、D、E为顶点的三角形与△AOC全等，求满足条件的点P，点E的坐标．7．如图，抛物线y＝x2+bx+c经过点（﹣2，5）和（2，﹣3），与两坐标轴的交点分别为A，B，C，它的对称轴为直线l．（1）求该抛物线的表达式；（2）求出点A，B，C的坐标；（3）P是该抛物线上的点，过点P作l的垂线，垂足为D，E是l上的点．要使以P，D，E为顶点的三角形与△BOC全等，求满足条件的点P，点E的坐标．8．如图，抛物线y＝ax2+bx﹣3与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C，点D是抛物线的顶点．（1）求抛物线的解析式．（2）直线BC交对称轴于点E，P是坐标平面内一点，请直接写出△PCE与△ACD全等时点P的坐标．9．如图1，抛物线y1＝ax2﹣x+c与x轴交于点A和点B（1，0），与y轴交于点C（0，），抛物线y1的顶点为G，GM⊥x轴于点M．将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2．（1）求抛物线y2的解析式；（2）点P为抛物线y1上一动点，过点P作y轴的平行线交抛物线y2于点Q，点Q关于直线l的对称点为R，若以P，Q，R为顶点的三角形与△AMG全等，求直线PR的解析式．10．如图，抛物线y＝x2+bx+c经过点A（﹣1，0），B（0，﹣2），并与x轴交于点C，点M是抛物线对称轴l 上任意一点（点M，B，C三点不在同一直线上）．（1）求该抛物线所表示的二次函数的表达式；（2）在抛物线上找出两点P1，P2，使得△MP1P2与△MCB全等，并求出点P1，P2的坐标；。

二次函数相似综合专题知识要点1．求抛物线的解析式（载体作用，注意利用顶点式隐藏顶点坐标或利用比根式隐藏与x 轴两交点的坐标）．2．结合质点运动，探索两个几何变量之间的函数关系； 3．探索存在问题（面积、线段、角度等）； 4．几何最值、几何定值与几何推理；5．全等、相似、轴对称、旋转、平移、解直角三角形、圆的相关知识的综合运用； 6．注意结合抛物线的图象变换构建存在性问题． 例题解析【例1】已知抛物线y ＝223x x --与x 轴交于A ，B 两点，与y 轴交于点C ．①若抛物线的顶点为M ，求四边形ACMB 的面积； ②在第一象限的抛物线上求点P ，使S △ABP ＝10； ③在第一象限的抛物线上求点P ，使S △ACP ＝10； ④在②的条件下，在抛物线上求点Q ，使S △APQ ＝S △BPQ ；⑤在②的条件下，在抛物线上求点Q ，使S △APQ ∶S △BPQ ＝1∶3．〖练1〗如图，□OABC 中，点A 坐标为（2，0），抛物线y ＝24ax bx ++经过点A ，B ，C三点，交y 轴于点D ． ①求此抛物线的解析式；②P 是抛物线上一点，且△OBP ≌△ODP ，求P 点坐标；③直线MN ∥x 轴，交抛物线于N ，交y 轴于M ，连线段BN ，AM ，BN 交OD 于E ，若AM ∥BN ，求线段MN 的长．第①问图第②问图第③问图【例2】已知△ABC为直角三角形，∠ACB＝90°，AC＝BC，点A，C在x轴上，点B坐标为（3，m）（m＞0），线段AB与y轴相交于点D，以P（1，0）为顶点的抛物线过点B，D．（1）求点A的坐标（用m表示）；（2）求抛物线的解析式；（3）设点Q为抛物线上点P至点B之间的一动点，连结PQ并延长交BC于点E，连结BQ并延长交AC于点F，试证明：FC（AC＋EC）为定值．【例3】如图，在平面直角坐标系中，点O为坐标原点，直与x轴交于点A，过点A的抛物线y＝2ax bx+与直线y＝4x-+交于另一点B，且点B的横坐标为1．（1）求a，b的值；（2）点P是线段AB上一动点（点P不与点A，B重合），过点P作PM∥OB交第一象限内的抛物线于点M，过点M作MC⊥x轴于点C，交AB于点N，过点P作PF⊥MC于点F，设PF的长为t，MN的长为d，求d与t之间函数关系式（不要求写出自变量的取值范围）；（3）在（2）的条件下，当S△ACN＝S△PMN时，连接ON，点Q在线段BP上，过点Q 作QR∥MN交ON于点R，连接MQ，BR，当∠MQR－∠BRN＝45°时，求点R的坐标．〖练2〗已知抛物线C 1：y ＝223x x --与x 轴交于A ，B 两点（A 在B 点左侧），与y 轴交于点C ．（1）求A ，B ，C 三点坐标；（2）将抛物线向右平移2个单位，向上平移3个单位，得到抛物线C 2，将线段AC绕坐标平面内的某点旋转后，得到线段MN ，且MN ⊥AC ，M ，N 点恰好落在抛物线C 2上，如图，求M 点的坐标；（3）设抛物线C 1的顶点为D ，DE ⊥AB 于E ，M 为x 轴下方抛物线C 1上一动点（不与点D 重合），MN ⊥BC 于N ，是否存在这样的点M ，使△MND 与△BED 相似？若存在，求M 点的坐标；若不存在，请说明理由．【例4】在平面直角坐标系xOy 中，已知抛物线y ＝24(2)9x c --+与x 轴交于A ，B 两点（点A 在点B 的左侧），交y 轴的正半轴于点C ，其顶点为M ，MH ⊥x 轴于点H ，MA 交y 轴于为N ，sin ∠MOH． （1）求此抛物线的函数表达式；（2）过H 的直线与y 轴相交于点P ，过O ，M 两点作直线PH 的垂线，垂足分别为E ，F ，若HE HF＝12JF ，求点P 的坐标； （3）将（1）中的抛物线沿y 轴折叠，使点A 落在点D 处，连接MD ，Q 为（1）中的抛物线上一动点，直线NQ 交x 轴于点G ，当Q 点在抛物线上运动时，是否存在点Q ，使△ANG 与△ADM 相似？若存在，求出所有符合条件的直线QG 的解析式；若不存在，请说明理由．〖练3〗抛物线y ＝2(1)4a x --的顶点为D ，与x 轴交于A ，B 两点，与y 轴负半轴交于点C ，对称轴与x 轴交于点H ，且HD ＝AB ． （1）求此抛物线的解析式；（2）若M 为对称轴右侧抛物线上一点，MN ∥x 轴交抛物线于另一点N ，以MN 为斜边的直角三角形的直角顶点在x 轴上，当这个直角三角形的顶点至少有一个时，求M 点纵坐标的取值范围；（3）经过C ，D 两点的直线与x 轴交于E 点，P 为对称轴右侧抛物线上一点，CP交对称轴于点F ，是否存在这样一点P ，使△CDF 与△EAC 相似、若存在，求点P 的坐标；若不存在，请说明理由．【例5】已知抛物线C 1：y ＝2(1)2a x +-的顶点为A ，且经过点B （－2，－1）．（1）求A 点的坐标和抛物线C 1的解析式；（2）如图1，将抛物线C 1向下平移2个单位后得到抛物线C 2，且抛物线C 2与直线AB 相交于C ，D 两点，求S △OAC ∶S △OAD 的值；（3）如图2，若过P （－4，0），Q （0，2）的直线为l ，点E 在（2）中抛物线C 2对称轴右侧部分（含顶点）运动，直线m 过点C 和点E ．问：是否存在直线m，使直线l ，m 与x 轴围成的三角形和直线l ，m 与y 轴围成的三角形相似？若存在，求出直线m 的解析式；若不存在，请说明理由．〖练4〗如图1，抛物线C 1：y ＝2ax bx c ++的顶点为A （1，134-），与y 轴的负半轴交于点B ．（1）求点B 的坐标；（2）如图2，将抛物线C 1向下平移与直线AB 相交于C ，D 两点，若BC ＋AD ＝AB ，求平移后的抛物线C 2的解析式；（3）如图3，在（2）中，设抛物线C 2与y 轴交于G 点，顶点为E ，EF ⊥x 轴于F点，点M （m ，0）是x 轴上一动点，点N 在线段EF 上，若∠MNG ＝90°，请你分析实数m 的变化范围；图1图2图1图3图2【例6】如图，已知抛物线y ＝2x bx c ++与x 轴交于点A （1，0）和点B ，与y 轴交于点C（0，－3）．（1）求抛物线的解析式；（2）如图1，已知点H （0，－1），问在抛物线上是否存在点G （点G 在y 轴的左侧），使得S △GHC ＝S △GHA ？若存在，求出点G 的坐标；若不存在，请说明理由； （3）如图2，抛物线上点D 在x 轴上的正投影为点E （－2，0），F 是OC 的中点，连接DF ，P 为线段BD 上的一点，若∠EPF ＝∠BDF ，求线段PE 的长．〖练5〗如图，抛物线1y ＝22ax ax b -+经过点A （－1，0），C （0，32）两点，与x 轴交于点一点B ．（1）求此抛物线的解析式；（2）若抛物线的顶点为M ，点P 为线段OB 上一动点（不与点B 重合），点Q 在线段MB 上移动，且∠MPQ ＝45°，设线段OP ＝x ，MQ2y ，求2y 与x 的函数关系式，并直接写出自变量x 的取值范围；（3）在同一平面直角坐标系中，两条直线x ＝m ，x ＝n 分别与抛物线交于点E ，G ，与（2）中的函数图象交于点F ，H ，问四边形EFGH 能否为平行四边形？若能，求出m ，n 之间的数量关系；若不能，请说明理由．图1图2【例7】如图1，抛物线y ＝(1)(3)a x x -+交x 轴于A ，B 两点，交y 轴于点C ，OC 2＝3OA ·OB ．（1）求此抛物线的解析式；（2）如图2，点E 为线段OA 上的一点，过点E 且垂直x 轴的直线交抛物线于点F ，若直线AC 将△AEF 分成面积之比为1∶2的两部分，求点E 的坐标；（3）如图3，若直线y ＝12x b +交x 轴于点M ，交y 轴于点N ，将△MON 沿直线MN 折叠，得到△MPN ，点O 的对称点为P ，是否存在这样的b 值，使点P 恰好落在抛物线上？若存在，求出b 的值；若不存在，请说明理由．〖练6〗如图1，抛物线y ＝2(21)4a x ax b --+与x 轴交于A ，B 两点，与y 轴正半轴交于点C ，直线BC 的解析式：y ＝3kx k -，tan ∠OCB ＝1． （1）求此抛物线的解析式；（2）如图2，若y 轴负半轴上点M ，此抛物线上点N ，关于直线AC 对称，求点N的坐标；（3）设D 为该抛物线的顶点，在此抛物线的对称轴上是否存在一点P ，使得△P AD与△ABC 相似、若存在，请求出点P 的坐标；若不存在，请说明理由．备用图【例8】在平面直线坐标系中，抛物线y ＝23ax bx ++交x 轴于A ，B 两点（A 点在B 点左侧），交y 轴于C 点，对称轴为直线x ＝1，sin ∠OCA． （1）求此抛物线的解析式，并求顶点E 的坐标；（2）将（1）中的抛物线向下平移，若平移后，在四边形ABEC 中满足S△BCE＝S △ABC ，求此时直线BC 的解析式；（3）将（1）中的抛物线作适当的平移，若平移后，在四边形ABED 中满足S △BCE＝2S △AOC ，且顶点E 恰好落在直线y ＝43x -+上，求此时抛物线的解析式．〖练7〗如图1，在平面直角坐标系中，直线l ：y ＝3342x --沿x 轴翻折后，与x 轴交于点A ，与y 轴交于点B ，抛物线y ＝22()3x h -与y 轴交于点D ，与直线AB 交于点E ，F （点F 在点E 的右侧）． （1）求直线AB 的解析式；（2）若线段DF ∥x 轴，求抛物线的解析式；（3）如图2，在（2）的条件下，过F 作FH ⊥x 轴于点G ，与直线l 交于点H，在备用图备用图抛物线上是否存在P ，Q 两点（点P 在点Q 的上方），PQ 与AP 交于点M ，与FH 交于点N ，使得直线PQ 既平分△AFH 的周长又平分△AFH 的面积？如果存在，求出P ，Q 的坐标；若不存在，请说明理由．图2图1。

相似与二次函数综合练习题1.如图，等腰梯形ABCD中，AD∥BC,AB=DC=5,AD=2,BC=8,∠MEN=∠B,∠MEN的顶角E在边BC上移动，一条边始终经过点A,另一边与CD交与点F,连接AF.(1)设BE=x，DF=y，试建立y关于x的函数关系式，并写出函数自变量x的取值范围；(2)若△AEF为等腰三角形，求出BE的长。

2.在平面直角坐标系中，已知点A(4,0),点B(0,3),点P从点A出发，以每秒1个单位的速度向右平移，点Q从点B出发，以每秒2个单位的速度向右平移，又P、Q两点同时出发。

(1)连接AQ,当△ABQ是直角三角形时，求点Q的坐标；(2)当P、Q运动到某个位置时，如果沿着直线AQ翻折，点P恰好落在线段AB上，求这时∠AQP的度数；(3)过点A作AC AB,AC交射线PQ于点C,连接BC,D是BC的中点，在点P、Q的运动过程中，是否存在某时刻，使得以A、C、Q、D为顶点的四边形是平行四边形，若存在，试求出这时tan∠ABC的值；若不存在，请说明理由。

3.如图，将一块直角三角纸板的直角顶点C(1,0.5)处，两直角边分别是x 、y 轴平行，纸板的另两个顶点A 、B 恰好是直线29+=kx y 与双曲线)0(>=m x m y 的交点，(1)求m 和k 的值；(2)设双曲线)0(>=m xm y 在A 、B 之间的部分为L,让一把三角尺的直角顶点P 在L 上滑动，两直角边始终与坐标轴平行，且与线段AB 交于M 、N 两点，请探究是否存在点P 使得MN=AB 21，写出你的探究过程。

4.把两块全等的直角三角形ABC 和DEF 叠放在一起，使三角板DEF 的锐角顶点D 与三角板ABC 的斜边中点O 重合，其中∠ABC=∠DEF=900,∠C=∠F=450,AB=DE=4,把三角板ABC 固定不动，让三角板DEF 绕点O 旋转，设射线DE 与射线AB 相交于点P ，射线DF 与线段BC 相交于点Q.(1)如图1，当射线DF 经过点B,即点Q 与点B 重合时，易证△APD ∽△CDQ,此时AP ·CQ= (2)将三角板DEF 由图1所示的位置绕点O 沿逆时针方向旋转，设旋转角为α，其中00900<<α，问AP ·CQ 的值是否改变？说明你的理由。

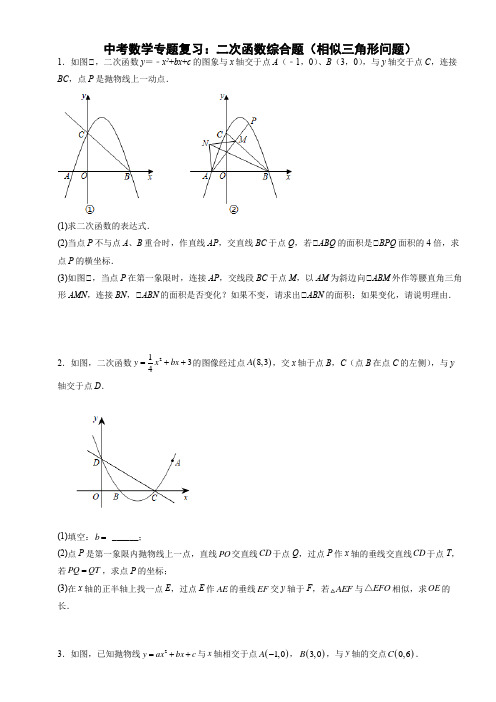
中考数学专题复习：二次函数综合题（相似三角形问题）1．如图①，二次函数y ＝﹣x 2+bx +c 的图象与x 轴交于点A （﹣1，0）、B （3，0），与y 轴交于点C ，连接BC ，点P 是抛物线上一动点．(1)求二次函数的表达式．(2)当点P 不与点A 、B 重合时，作直线AP ，交直线BC 于点Q ，若①ABQ 的面积是①BPQ 面积的4倍，求点P 的横坐标．(3)如图①，当点P 在第一象限时，连接AP ，交线段BC 于点M ，以AM 为斜边向①ABM 外作等腰直角三角形AMN ，连接BN ，①ABN 的面积是否变化？如果不变，请求出①ABN 的面积；如果变化，请说明理由．2．如图，二次函数2314y x bx =++的图像经过点()8,3A ，交x 轴于点B ，C （点B 在点C 的左侧），与y 轴交于点D ．(1)填空：b = ______；(2)点P 是第一象限内抛物线上一点，直线PO 交直线CD 于点Q ，过点P 作x 轴的垂线交直线CD 于点T ，若PQ QT =，求点P 的坐标；(3)在x 轴的正半轴上找一点E ，过点E 作AE 的垂线EF 交y 轴于F ，若AEF 与EFO △相似，求OE 的长．3．如图，已知抛物线2y ax bx c =++与x 轴相交于点()1,0A -，()3,0B ，与y 轴的交点()0,6C ．(1)求抛物线的解析式；(2)点(),P m n 在平面直角坐标系第一象限内的抛物线上运动，设PBC 的面积为S ，求S 关于m 的函数表达式(指出自变量m 的取值范围)和S 的最大值；(3)点M 在抛物线上运动，点N 在y 轴上运动，是否存在点M 、点N 使得①CMN ＝90°，且∆CMN 与OBC ∆相似，如果存在，请求出点M 和点N 的坐标．4．如图，抛物线L 1：y ＝ax 2﹣2x ＋c （a ≠0）与x 轴交于A 、B （3，0）两点，与y 轴交于点C （0，﹣3），抛物线的顶点为D ．抛物线L 2与L 1关于x 轴对称．(1)求抛物线L 1与L 2的函数表达式；(2)已知点E 是抛物线L 2的顶点，点M 是抛物线L 2上的动点，且位于其对称轴的右侧，过M 向其对称轴作垂线交对称轴于P ，是否存在这样的点M ，使得以P 、M 、E 为顶点的三角形与△BCD 相似，若存在请求出点M 的坐标，若不存在，请说明理由．5．如图，在平面直角坐标系中，已知直线4y x =+与x 轴、y 轴分别相交于点A 和点C ，抛物线21y x kx k =++-的图象经过点A 和点C ，与x 轴的另一个交点是点B ．(1)求出此抛物线的解析式； (2)求出点B 的坐标；(3)若在y 轴的负半轴上存在点D ．能使得以A ，C ，D 为顶点的三角形与①ABC 相似，请求出点D 的坐标．6．如图1，已知抛物线23y ax bx =++经过点()1,5D ，且交x 轴于A ，B 两点，交y 轴于点C ，已知点()1,0A -，(),P m n 是抛物线在第一象限内的一个动点，PQ BC ⊥于点Q ．(1)求抛物线的解析式；(2)当PQ =m 的值；(3)是否存在点P ，使BPQ 与BOC 相似？若存在，请求出P 点的坐标；若不存在，请说明理由．7．如图，在平面直角坐标系中，直线y ＝12x ＋2与x 轴交于点A ，与y 轴交于点C ．抛物线y ＝ax 2＋bx ＋c的对称轴是x＝－32且经过A、C两点，与x轴的另一交点为点B．(1)求二次函数y＝ax2＋bx＋c的表达式；(2)点P为线段AB上的动点，求AP＋2PC的最小值；(3)抛物线上是否存在点M，过点M作MN垂直x轴于点N，使得以点A，M，N为顶点的三角形与①ABC 相似？若存在，求出点M的坐标；若不存在，请说明理由．8．如图，抛物线y=−x2+bx+c与x轴相交于A(−1，0)，B(3，0)两点，与y轴交于点C，顶点为点D，抛物线的对称轴与BC相交于点E，与x轴相交于点F．(1)求抛物线的函数关系式；(2)连结DA，求sin A的值；(3)若点H线段BC上，BOC与BFH△相似，请直接写出点H的坐标．9．如图，抛物线y＝1-2x2+bx+c与x轴交于点A（﹣2，0）和点B（8，0），与y轴交于点C，顶点为D，连接AC，BC，BC与抛物线的对称轴l交于点E．(1)求抛物线的表达式；(2)点P 是第一象限内抛物线上的动点，连接PB ，PC ，当S △PBC ＝720S △ABC 时，求点P 的坐标； (3)点N 是对称轴l 右侧抛物线上的动点，在射线ED 上是否存在点M ，使得以点M ，N ，E 为顶点的三角形与①OBC 相似？若存在，求点M 的坐标；若不存在，请说明理由．10．如图，抛物线23y ax bx =++与x 轴交于1,0A 、()3,0B -两点，与y 轴交于点C ，设抛物线的顶点为D ．(1)求该抛物线的表达式与顶点D 的坐标； (2)试判断BCD △的形状，并说明理由；(3)探究坐标轴上是否存在点P ，使得以P 、A 、C 为顶点的三角形与BCD △相似？若存在，请求出点P 的坐标；若不存在，请说明理由．11．如图，抛物线y ＝ax 2﹣2ax ﹣3a （a ≠0）与x 轴交于点A ，B ．与y 轴交于点C ．连接AC ，BC ．已知ABC 的面积为2．(1)求抛物线的解析式；(2)平行于x 轴的直线与抛物线从左到右依次交于P ，Q 两点．过P ，Q 向x 轴作垂线，垂足分别为G ，H ．若四边形PGHQ 为正方形，求正方形的边长；(3)抛物线上是否存在一点N ，使得①BCN ＝①CAB ﹣①CBA ，若存在，请求出满足条件N 点的横坐标，若不存在请说明理由．12．如图，二次函数2y x bx c =-++的图像与x 轴交于点A （－1，0），B （2，0），与y 轴相交于点C ．(1)求这个二次函数的解析式；(2)若点M 在此抛物线上，且在y 轴的右侧．①M 与y 轴相切，过点M 作MD ①y 轴，垂足为点D ．以C ，D ，M 为顶点的三角形与①AOC 相似，求点M 的坐标及①M 的半径长．13．如图，在平面直角坐标系中，抛物线2()0y ax bx c ac =++≠与x 轴交于点A 和点B （点A 在点B 的左侧），与y 轴交于点C ．若线段OA OB OC 、、的长满足2OC OA OB =⋅，则这样的抛物线称为“黄金”抛物线．如图，抛物线22(0)y ax bx a =++≠为“黄金”抛物线，其与x 轴交点为A ，B （其中B 在A 的右侧），与y 轴交于点C ．且4OA OB =(1)求抛物线的解析式；(2)若P 为AC 上方抛物线上的动点，过点P 作PD AC ⊥，垂足为D ． ①求PD 的最大值；①连接PC ，当PCD 与ACO △相似时，求点P 的坐标．14．如图，在平面直角坐标系xOy 中，已知抛物线2y x bx c =++与x 轴交于点A 、B 两点，其中1,0A ，与y 轴交于点()0,3C ．(1)求抛物线解析式；(2)如图1，过点B 作x 轴垂线，在该垂线上取点P ，使得①PBC 与①ABC 相似，请求出点P 坐标；(3)如图2，在线段OB 上取一点M ，连接CM ，请求出12CM BM +最小值．15．如图，抛物线y ＝ax 2+k （a ＞0，k ＜0）与x 轴交于A ，B 两点（点B 在点A 的右侧），其顶点为C ，点P 为线段OC 上一点，且PC ＝14OC ．过点P 作DE ①AB ，分别交抛物线于D ，E 两点（点E 在点D 的右侧），连接OD ，DC ．(1)直接写出A ，B ，C 三点的坐标；（用含a ，k 的式子表示） (2)猜想线段DE 与AB 之间的数量关系，并证明你的猜想；(3)若①ODC ＝90°，k ＝﹣4，求a 的值．16．如图，抛物线223y x bx c =++与x 轴交于A ，B 两点，与y 轴交于C 点，连接AC ，已知B (﹣1，0)，且抛物线经过点D (2，﹣2)．(1)求抛物线的表达式；(2)若点E 是抛物线上第四象限内的一点，且2ABES=，求点E 的坐标；(3)若点P 是y 轴上一点，以P ，A ，C 三点为顶点的三角形是等腰三角形，求P 点的坐标．17．如图，在直角坐标系xOy 中，抛物线y ＝ax 2＋bx ＋2（a ≠0）与x 轴交于点A （﹣1，0）和B （4，0），与y 轴交于点C ，点P 是抛物线上的动点（不与点A ，B ，C 重合）．(1)求抛物线的解析式；(2)当点P 在第一象限时，设①ACP 的面积为S 1，①ABP 的面积为S 2，当S 1＝S 2时，求点P 的坐标； (3)过点O 作直线l ①BC ，点Q 是直线l 上的动点，当BQ ①PQ ，且①BPQ ＝①CAB 时，请直接写出点P 的坐标．18．如图，在平面直角坐标系xOy中，直线y＝﹣x＋3与两坐标轴交于A、B两点，抛物线y＝x2＋bx＋c 过点A和点B，并与x轴交于另一点C，顶点为D．点E在对称轴右侧的抛物线上．(1)求抛物线的函数表达式和顶点D的坐标；(2)若点F在抛物线的对称轴上，且EF①x轴，若以点D，E，F为顶点的三角形与①ABD相似，求出此时点E的坐标；(3)若点P为坐标平面内一动点，满足tan①APB＝3，请直接写出①P AB面积最大时点P的坐标及该三角形面积的最大值．19．如图，在平面直角坐标系中，抛物线y＝ax2＋bx＋c（a≠0）与x轴交于点A、B，与y轴交于点C，且OC＝2OB＝6OA＝6，点P是第一象限内抛物线上的动点．(1)求抛物线的解析式；(2)连接BC与OP，交于点D，当S△PCD：S△ODC的值最大时，求点P的坐标；(3)点M在抛物线上运动，点N在y轴上运动，是否存在点M、点N．使①CMN＝90°，且①CMN与①BOC 相似，若存在，请求出点M、点N的坐标．20．如图，抛物线y＝x2＋bx＋12（b＜0）与x轴交于A，B两点（A点在B点左侧），且OB＝3OA．(1)请直接写出b＝，A点的坐标是，B点的坐标是；(2)如图（1），D点从原点出发，向y轴正方向运动，速度为2个单位长度/秒，直线BD交抛物线于点E，若BE＝5DE，求D点运动时间；(3)如图（2），F点是抛物线顶点，过点F作x轴平行线MN，点C是对称轴右侧的抛物线上的一定点，P 点在直线MN上运动．若恰好存在3个P点使得①P AC为直角三角形，请求出C点坐标，并直接写出P点的坐标．答案1．(1)y ＝﹣x 2+2x +3．(2)P 352或 (3)①ABN 的面积不变，为4．2．(1)2-(2)5⎛ ⎝⎭或5⎛ ⎝⎭(3)4或493．(1)2246y x x =-++(2)S 关于m 的函数表达式为239(03)S m m m =-+<<，S 的最大值是274 (3)存在，M （1，8），N （0，172）或M （74，558），N （0，838）或M （94，398），N （0，38）或M （3，0），N （0，﹣32）4．(1)抛物线L 1：223y x x =--，抛物线L 2：2y x 2x 3=-++；(2)435(,)39M 或(4,5)M -．5．(1)254y x x =++(2)点B 的坐标为（－1，0）(3)点D 的坐标是（0，－203） 6．(1)215322y x x =-++ (2)1或5(3)存在；P （53，529）7．(1)抛物线表达式为：213222y x x =--+；(2)AP +2PC 的最小值是4；(3)存在M(0,2)或(-3,2)或(2,-3)或(5,-18)，使得以点A 、M 、N 为顶点的三角形与ABC 相似．8．(1)y =-x 2+2x +3(3)点H 的坐标为(1，2)或(2，1)9．(1)21382y x x =++ (2)P 1（1，10.5），P 2（7，4.5）(3)存在，（3，8）或(3,5或（3，11）30．(1)y ＝﹣x 2﹣2x +3，（﹣1，4）；(2)直角三角形，理由见解析；(3)存在，（0，0）或（0，﹣13）或（－9，0）11．(1)y ＝﹣13x 2+23x +1(2)﹣6﹣(3)存在，5或11712．(1)22y x x =-++； (2)M 的坐标为（12，94），（32， 54 ），（3，-4），①M 的半径长为12或32或313．(1)213222y x x =--+(2)①PD ①P 坐标为(3,2)-或325()28，-14．(1)243y x x =-+(2)P 点坐标为()3,9或()3,215．(1)点A 、B 、C 的坐标分别为(、、(0，k ) (2)DE ＝12AB(3)a ＝1316．(1)224233y x x =--(2)E ，-1)(3)P 点的坐标(0，2)或(02)或(0，﹣2或(0，54)17．(1)213222y x x =-++ (2)点P 的坐标为（103，139）(3)点P 的坐标为（32，﹣2）或（32，﹣2）或（173，﹣509）18．(1)y ＝x 2﹣4x +3，（2，﹣1）(2)（5，8）或（73，89-）(3)①P AB ，此时P ）19．(1)y ＝﹣2x 2+4x +6 (2)点P 的坐标为（32，152） (3)存在，M 、N 的坐标分别为（3，0）、（0，﹣32）或（94，398）、（0，38）或（1，8）、（0，172）或（74，558）、（0，838）20．(1)﹣8，（2，0），（6，0）(2)3秒或212秒 (3)C 点坐标为（143，﹣329），P 点的坐标为（103，﹣4）或（﹣103，﹣4）或（11027，﹣4）。

二次函数存在性问题——相似三角形例一、如图，抛物线y=ax2+bx+c（a≠0）经过点A（﹣3，0）、B（1，0）、C（﹣2，1），交y轴于点M．（1）求抛物线的表达式；（2）D为抛物线在第二象限部分上的一点，作DE垂直x轴于点E，交线段AM于点F，求线段DF长度的最大值，并求此时点D的坐标；（3）抛物线上是否存在一点P，作PN垂直x轴于点N，使得以点P、A、N为顶点的三角形与△MAO相似？若存在，求点P的坐标；若不存在，请说明理由．例二.如图，已知抛物线经过A（﹣2，0），B（﹣3，3）及原点O，顶点为C（1）求抛物线的函数解析式．（2）设点D在抛物线上，点E在抛物线的对称轴上，且以AO为边的四边形AODE是平行四边形，求点D的坐标．（3）P是抛物线上第一象限内的动点，过点P作PM⊥x轴，垂足为M，是否存在点P，使得以P，M，A为顶点的三角形与△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由．随堂练习1.如图，抛物线21y ax bx =++与x 轴交于A （-1，0）、B （1，0）两点，与y 轴交于点C ．（1）求抛物线的解析式；（2）过点B 作BD ∥CA 与抛物线交于点D ，求四边形ACBD 的面积；（3）M 是x 轴下方抛物线上的一个动点，过M 作MN ⊥x 轴于点N ，是否存在点M ，使以A 、M 、N 为顶点的三角形与△BCD 相似？若存在，请求出点M 的坐标；若不存在，请说明理由．2. 如图，在平面直角坐标系xOy 中，直线y=x+4与坐标轴分别交于A 、B 两点，过A 、B 两点的抛物线为y=﹣x2+bx+c．点D为线段AB上一动点，过点D作CD⊥x 轴于点C，交抛物线于点E．（1）求抛物线的解析式．（2）当DE=4时，求四边形CAEB的面积．（3）连接BE，是否存在点D，使得△DBE和△DAC相似？若存在，求此点D坐标；若不存在，说明理由．3.如图，抛物线y=ax2+b与x轴交于点A、B，且A点的坐标为（1，0），与y轴交于点C（0，1）．（1）求抛物线的解析式，并求出点B坐标；（2）过点B作BD∥CA交抛物线于点D，连接BC、CA、AD，求四边形ABCD的周长；（结果保留根号）（3）在x轴上方的抛物线上是否存在点P，过点P作PE垂直于x轴，垂足为点E，使以B、P、E为顶点的三角形与△CBD 相似？若存在请求出P点的坐标；若不存在，请说明理由．4.如图所示，直线l：y=3x+3与x轴交于点A，与y轴交于点B．把△AOB沿y轴翻折，点A落到点C，抛物线过点B、C 和D（3，0）．（1）求直线BD和抛物线的解析式．（2）若BD与抛物线的对称轴交于点M，点N在坐标轴上，以点N、B、D为顶点的三角形与△MCD相似，求所有满足条件的点N的坐标．（3）在抛物线上是否存在点P，使S△PBD=6？若存在，求出点P的坐标；若不存在，说明理由．5. 如图，四边形ABCD是平行四边形，AB=4，OB=2，抛物线过A、B、C三点，与x轴交于另一点D．一动点P以每秒1个单位长度的速度从B点出发沿BA向点A运动，运动到点A停止，同时一动点Q从点D出发，以每秒3个单位长度的速度沿DC向点C运动，与点P同时停止．（1）求抛物线的解析式；（2）若抛物线的对称轴与AB交于点E，与x轴交于点F，当点P运动时间t为何值时，四边形POQE是等腰梯形？（3）当t为何值时，以P、B、O为顶点的三角形与以点Q、B、O为顶点的三角形相似？6. 如图，抛物线y=ax2﹣2ax+c（a≠0）交x轴于A、B两点，A点坐标为（3，0），与y轴交于点C（0，4），以OC、OA为边作矩形OADC交抛物线于点G．（1）求抛物线的解析式；（2）抛物线的对称轴l在边OA（不包括O、A两点）上平行移动，分别交x轴于点E，交CD于点F，交AC于点M，交抛物线于点P，若点M的横坐标为m，请用含m的代数式表示PM的长；（3）在（2）的条件下，连结PC，则在CD上方的抛物线部分是否存在这样的点P，使得以P、C、F为顶点的三角形和△AEM相似？若存在，求出此时m的值，并直接判断△PCM的形状；若不存在，请说明理由．。

一、二次函数性质1. 已知二次函数f(x) = ax^2 + bx + c，其中a、b、c为实数，且a ≠ 0。

若f(x)的对称轴为x = 1，且f(0) = 2，求f(x)的解析式。

2. 设二次函数f(x) = ax^2 + bx + c的图象开口向上，且f(1) = 3，f(1) = 1，求f(x)的解析式。

3. 已知二次函数f(x) = ax^2 + bx + c的图象与x轴有两个交点，且f(0) = 1，f(1) = 3，求f(x)的解析式。

4. 设二次函数f(x) = ax^2 + bx + c的图象开口向下，且f(1) = 3，f(1) = 1，求f(x)的解析式。

5. 已知二次函数f(x) = ax^2 + bx + c的图象与x轴有两个交点，且f(0) = 1，f(2) = 3，求f(x)的解析式。

二、二次函数图像1. 已知二次函数f(x) = ax^2 + bx + c的图象开口向上，且顶点坐标为(1, 2)，求f(x)的解析式。

2. 设二次函数f(x) = ax^2 + bx + c的图象开口向下，且顶点坐标为(1, 3)，求f(x)的解析式。

3. 已知二次函数f(x) = ax^2 + bx + c的图象与x轴有两个交点，且顶点坐标为(0, 1)，求f(x)的解析式。

4. 设二次函数f(x) = ax^2 + bx + c的图象开口向上，且顶点坐标为(2, 3)，求f(x)的解析式。

5. 已知二次函数f(x) = ax^2 + bx + c的图象开口向下，且顶点坐标为(1, 2)，求f(x)的解析式。

三、二次函数图像变换1. 已知二次函数f(x) = x^2的图象，求函数g(x) = (x 1)^2 + 2的图象。

2. 设二次函数f(x) = x^2的图象，求函数g(x) = (x + 2)^2 3的图象。

3. 已知二次函数f(x) = x^2的图象，求函数g(x) = (x 1)^22的图象。

二次函数与相似椭圆结合专题练习一、二次函数1. 课前预1. 熟悉二次函数的标准式，顶点式和描点式。

2. 了解二次函数的图像特征：对称轴、顶点坐标、开口方向和大小等。

2. 课堂练2.1 选择题1. 已知函数 $f(x)=2x^2-4x+1$，则 $f(1)=$_____。

A. $-1$B. $-1/2$C. $1$D. $9$2. 二次函数 $y=3(x-2)^2$ 的对称轴方程是_____。

A. $x=2$B. $x=-2$C. $y=2$D. $y=-2$3. 将 $y=2x^2-4x+1$ 化为顶点式，那么其中顶点的坐标为_____。

A. $(-1,3)$B. $(1,-3)$C. $(1,3)$D. $(-1,-3)$2.2 解答题1. 已知二次函数 $y=-x^2+4x-5$ 的图像经过点 $P(1,2)$，求过点 $P$ 的切线方程。

2. 已知二次函数 $y=ax^2+bx+c$ 的图像与 $x$ 轴交于 $A,B$ 两点，$y$ 轴上的截距为$4$，且$\abs{AC}=\dfrac{1}{2}\abs{AB}$，那么 $a=$_______。

二、相似椭圆1. 课前预1. 熟悉椭圆的数学定义及相关专有名词。

2. 了解椭圆方程的一般形式。

2. 课堂练2.1 选择题1. 下列椭圆方程中，正确的是_____。

A. $\dfrac{x^2}{4}+\dfrac{y^2}{25}=1$B. $\dfrac{x^2}{25}+\dfrac{y^2}{16}=1$C. $\dfrac{x^2}{16}+\dfrac{y^2}{25}=1$D. $\dfrac{x^2}{20}+\dfrac{y^2}{15}=1$2. 已知椭圆 $E$ 的中心为 $(1,2)$，离心率为 $\dfrac{1}{2}$，则 $E$ 的方程为_____。

A. $(x-1)^2+(y-2)^2=18$B. $\dfrac{(x-1)^2}{4}+\dfrac{(y-2)^2}{9}=1$C. $\dfrac{(x-1)^2}{9}+\dfrac{(y-2)^2}{4}=1$D. $\dfrac{(x-1)^2}{16}+\dfrac{(y-2)^2}{25}=1$3. 椭圆 $\dfrac{(x-2)^2}{25}+\dfrac{(y+1)^2}{16}=1$ 的周长为_____。

考前押题卷二一、选择题：1、在平面直角坐标系中，将抛物线4-2x y =先向右平移2个单位，再向上平移2个单位，得到的抛物线的解析式是（ ）A 、222++=）（x yB 、2-2-2）（x y =C 、22-2+=）（x yD 、2-22）（+=x y2、如图，小正方形的边长均为1，则下列图中的三角形（阴影部分）与△ABC 相似的是（ ）A B C D3、某学生在练习投篮时，篮球被抛出后距离地面的高度)(m h 和飞行时间)(s t 满足下面的函数关系式：2221-2++=t t h ，则篮球距离地面的最大高度是（ ） A 、m 8 B 、m 6 C 、m 4 D 、m 24、手工制作课上，小红利用一些花布的边角料，剪裁后装饰手工画，下面四个图案是她剪裁出的空心不等边三角形、等边三角形、正方形、矩形花边，其中，每个图案花边的宽度都相等，那么，每个图案中花边的内外边缘所围成的几何图形不相似的是（ ）A B C D5、二次函数c bx ax y ++=2的图象如图所示，给出下列说法：①0<abc ；②方程02=++c bx ax 的根为31-21==x x 、；③当x ＞1时，y 随x 值的增大而减小； ④当y ＞0时，-1＜x ＜3． 其中正确的说法是（ ）A 、②③④B 、①③④C 、①②③D 、①②③④6、如图，△PQR 在边长为1个单位的方格纸中，它的顶点在小正方形顶点位置，其中点A 、B 、C 、D 也是小正方形的顶点，那么与△PQR 相似的是（ ）A 、以点P 、Q 、A 为顶点的三角形；B 、以点P 、Q 、B 为顶点的三角形C 、以点P 、Q 、C 为顶点的三角形；D 、以点P 、Q 、D 为顶点的三角形7、已知二次函数m m x x y (3-2+=为常数）的图象与x 轴的一个交点为（1,0），则关于x 的一元二次方程03-2=+m x x 的两实数根是（ ）11=x ，1-2=x B 、11=x ，22=x C 、11=x ，02=x D 、11=x ，32=x8、图中两个四边形是位似图形，它们的位似中心是（ ）A 、点MB 、点NC 、点OD 、点P9、二次函数)0(2≠++=a c bx ax y 的图象如图所示，则下列说法不正确的是（ ）A 、04-2>ac b B 、0>a C 、0>c D 、02>ab10、如图，A ，B ，C ，D ，E ，G ，H ，M ，N 都是方格纸中的格点（即小正方形的顶点），要使△DEF 与△ABC 相似，则点F 应是G ，H ，M ，N 四点中的（ ）A 、H 或NB 、G 或HC 、M 或ND 、G 或M11、在同一平面直角坐标系中，函数m mx y +=和函数22-2++=x mx y （m 是常数，且0≠m ）的图象可能是（ ）A B C D12、在平面直角坐标系中，将抛物线2--2x x y =向上（下）或向左（右）平移m 个单位，使平移后的抛物线恰好经过原点，则|m|的最小值为（ ） A 、1 B 、2 C 、3 D 、613、若二次函数c x x y +=6-2的图象经过),23(),2()1-(321y C y B y A +、、，三点，则关于321y y y 、、大小关系正确的是（ ）A 、321y y y >>B 、231y y y >>C 、312y y y >>D 、213y y y >>14、如图，从地面竖直向上抛出一个小球，小球的高度h （单位：m ）与小球运动时间t （单位：s ）之间的关系式为h=30t-5t 2，那么小球从抛出至回落到地面所需要的时间是（ ）A 、6sB 、4sC 、3sD 、2s15、抛物线c bx ax y ++=2上部分点的横坐标x ，纵坐标y 的对应值如下表所示：x ．．． -3 -2 -1 0 1 ．．． y．．．-6466．．．给出下列说法：①抛物线与y 轴的交点为（0，6）；②抛物线的对称轴是在y 轴的右侧；③抛物线一定经过点（3，0）；④在对称轴左侧，y 随x 增大而减小．从表可知，下列说法正确的个数有（ ）A 、1个B 、2个C 、3个D 、4个16、某校校园内有一个大正方形花坛，它由四个边长均为3米的小正方形组成，如图（1），且每个小正方形的种植方案相同．其中的一个小正方形ABCD 如图（2），DG=1米，AE=AF=x 米，在五边形EFBCG 区域上种植花卉，则大正方形花坛种植花卉的面积y 与x 的函数图象大致是（ ）A B C D二、填空题17、如图，在边长为9的正三角形ABC 中，BD=3，°=∠60ADE ，则AE 的长为 ．18、在二次函数c bx x y ++=2中，函数值y 与自变量x 的部分对应值如下表：x -2 -1 0 1 2 3 4 y72-1-2m27则m 的值为 ．19、若把函数32-2+=x x y 化为k m x y +=2-）（，其中k m ，为常数，则=+k m ．20、已知点)5,(1x A 、)5,(2x B 是函数32-2+=x x y 上的两点，则当21x x x +=时，函数值=y ．21、如图，是小孔成像原理的示意图，根据图中标注的尺寸，如果物体AB 的高度为36cm ，那么它在暗盒中所成的像CD 的高度应为 cm ．三、解答题22、如图，在34×的正方形方格中，△ABC 和△DEC 的顶点都在边长为1的小正方形的顶点上．（1）填空：=ABC ∠ ，=BC ； （2）判断△ABC 与△CED 是否相似，并证明你的结论．23、如图，电线杆AB 的影子恰好落在山坡CD 和地面BC 上，测得CD=4m ，BC=10m ，CD 与地面成30°角，且此时直立的1m 的竹竿的影长是2m ，求电线杆AB 的高．24、如图，等腰梯形ABCD 中，AD//BC ，AD=3，BC=7,°=60∠B ，P 为BC 边上一点（不与B 、C 重合），过点P 作B APE ∠∠=，PE 交CD 于E ． （1）求证：△APB ∽△PEC ； （2）若CE=3，求BP 的长．25、在某居民小区要在一块一边靠墙（墙长15m）的空地上修建一个矩形花园ABCD，花园的一边靠墙，另三边用总长为40m的栅栏围成如图，若设花园的BC边长为x（m）花园的面积为y（m2）（1）求y与x之间的函数关系式，并求自变量的x的范围．（2）当x取何值时花园的面积最大，最大面积为多少？26、某宾馆有50个房间供游客住宿，当每个房间的房价为每天180元时，房间会全部住满．当每个房间每天的房价每增加10元时，就会有一个房间空闲．宾馆需对游客居住的每个房间每天支出20元的各种费用．根据规定，每个房间每天的房价不得高于340元．设每个房间的房价增加x元（x为10的正整数倍）．（1）设一天订住的房间数为y，直接写出y与x的函数关系式及自变量x的取值范围；（2）设宾馆一天的利润为w元，求w与x的函数关系式；（3）一天订住多少个房间时，宾馆的利润最大？最大利润是多少元？参考答案满分：100分一、选择题：（每题3分，共30分）1、B2、A3、C4、D5、D6、B7、B8、D9、D 10、C 11、D 12、A 13、B 14、A 15、C 16、A 二、填空题：（每题3分，共30分）17、7 18、-1 19、3 20、3 21、16 三、解答题：（22题8分，23题8分，24题12分，25题12分，合计40分） 22、（1）135°；22 （2）相似，证明略． 23、37+24、（1）相似（一线三等角）；（2）3或4．25、（1）)15≤0(2021-2x x x y <+=；（2）()21-202002y x =-+，∵1-02a =<，∴抛物线开口向下，又抛物线对称轴为：20x =，∴当015x <≤时，y 随x 的增大而增大，∴当15x =，最大面积187．52m ． 26、（1），160≤≤10(50101-x x y +=且x 是10的正整数倍）； （2）21-34800010w x x =++； （3）()21-1701089010w x =-+，∵1-010a =<，∴抛物线开口向下，又抛物线对称轴为：170x =，∴当10160x ≤≤时，w 随x 的增大而增大，∴当160x =，即34间，宾馆利润最大，最大利润是10880元．。

考前押题卷一一、选择题（每小题3分，共48分）1、下列函数关系中，可以看做二次函数)0≠(2a c bx ax y ++=模型的是（ ） A 、在一定的距离内汽车的行驶速度与行驶时间的关系；B 、我国人口年自然增长率1%，这样我国人口总数随年份的关系；C 、竖直向上发射的信号弹，从发射到落回地面，信号弹的高度与时间的关系（不计空气阻力）；D 、圆的周长与圆的半径之间的关系.2、图中两个四边形是位似图形，它们的位似中心是（ ）A.M B 、N C 、O D 、P 3、抛物线13-22+=）（x y 的顶点坐标是（ ）A 、（3,1）B 、（3，-1）C 、（-3,1）D 、（-3，-1）4、若有二次函数c ax y +=2，当x 取1x ，2x （21≠x x ）时，函数值相等，则当21x x x +=时，函数值为（ ）A 、c a +B 、c a -C 、c -D 、c5、把抛物线2--2x y =平移后得到抛物线2-x y =，平移的方法可以是（ ） A 、沿y 轴向上平移2个单位 B 、沿y 轴向下平移2个单位C 、沿x 轴向右平移2个单位D 、沿x 轴向左平移2个单位6、小华同学自制了一个简易的幻灯机，其工作情况如图所示，幻灯片与屏幕平行，光源到幻灯片的距离是30cm ，幻灯片到屏幕的距离是1.5m ，幻灯片上小树的高度是10cm ，则屏幕上小树的高度是（ ）A 、50cmB 、500cmC 、60cmD 、600cm7、下列4×4的正方形网格中，小正方形的边长均为1，三角形的顶点都在格点上，则与△ABC 相似的三角形所在的网格图形是（ ）A B C D8、如图，点D 在△ABC 的边AC 上，要判定△ADB 与△ABC 相似，添加一个条件，不正确的是（ ）A 、∠ABD=∠CB 、∠ADB=∠ABC C 、CD CB BD AB = D 、ACABAB AD = 9、如图，若A 、B 、C 、P 、Q 、甲、乙、丙、丁都是方格纸中的格点，为使ABC∽△PQR，则点R 应是甲、乙、丙、丁四点中的（ ）A 、甲B 、乙C 、丙D 、丁10、已知二次函数)0≠(2a c bx ax y ++=的y 与x 的对应值如下表： x ...... -1 0 1 3 ...... y......-3131......则下列判断中正确的是（ ）A 、抛物线开口向上B 、抛物线与y 轴交于负半轴C 、当x=4时，y>0D 、方程02=++c bx ax 的正根在3与4之间11、已知矩形ABCD 中，AB=1，在BC 上取一点E ，沿AE 将△ABE 向上折叠，使B 点落在AD 上的F 点，若四边形EFDC 与矩形ABCD 相似，则AD=（ ）A 、21-5 B 、215+ C 、3 D 、212、如图，在△ABC 中，AB=AC=2，∠BAC=20°．动点P 、Q 分别在直线BC 上运动，且始终保持∠PAQ=100°．设BP=x ，CQ=y ，则y 与x 之间的函数关系用图象大致可以表示为（ ）A B C D13、如图，在△ABC 中，点D ，E 分别在边AB ，AC 上，且21==AC AD AB AE ，则BCED AD E S S 四边形△：的值为（ ）A.3:1 B 、1:2 C 、1:3 D 、1:414、如图，Rt△ABC 中，∠ACB=90°，∠ABC=60°，BC=2cm ，D 为BC 的中点，若动点E 以1cm/s 的速度从A 点出发，沿着A→B→A 的方向运动，设E 点的运动时间为t 秒（0≤t＜6），连接DE ，当△BDE 是直角三角形时，t 的值为（ ）A 、2B 、2.5或3.5C 、3.5或4.5D 、2或3.5或4.515、已知二次函数)0≠(2a c bx ax y ++=的部分图象如图所示，若y<0，则x 的取值范围（ ）A 、-1<x<4B 、-1<x<3C 、x<-1或x>4D 、x<-1或x>316、下列表格是二次函数c bx ax y ++=2的自变量x 与函数值y 的对应值，判断方程为常数）、、（c b a a c bx ax ,002≠=++的一个解x 的范围是（ ） A 、17.66<<x B 、18.617.6<<x C 、19.618.6<<x D 、20.619.6<<x二、填空题：（每小题3分，共15分） 17、已知抛物线1--2x x y =与x 轴的一个交点为（m,0），则代数式的值为 。