5知识讲解_正弦函数的图象与性质_基础

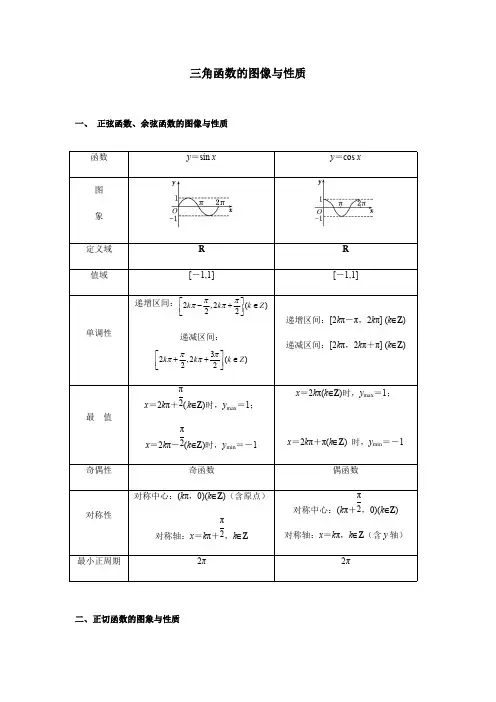
i ng si nt he i rb ei n ga re g三角函数的图像与性质一、 正弦函数、余弦函数的图像与性质二、正切函数的图象与性质函数y ＝sin x y ＝cos x图象定义域RR 值域[－1,1][－1,1]单调性递增区间：2,2()22k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦递减区间：32,2()22k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦递增区间：[2k π－π，2k π] (k ∈Z )递减区间：[2k π，2k π＋π] (k ∈Z )最　值x ＝2k π＋(k ∈Z )时，y max ＝1；π2x ＝2k π－(k ∈Z )时，y min ＝－1π2x ＝2k π(k ∈Z )时，y max ＝1；x ＝2k π＋π(k ∈Z ) 时，y min ＝－1奇偶性奇函数偶函数对称性对称中心：(k π，0)(k ∈Z )（含原点）对称轴：x ＝k π＋，k ∈Zπ2对称中心：(k π＋，0)(k ∈Z )π2对称轴：x ＝k π，k ∈Z （含y 轴）最小正周期2π2π定义域{|,}2x x k k Z ππ≠+∈值域R单调性递增区间(,)()22k k k Z ππππ-+∈奇偶性奇函数对称性对称中心：（含原点）(,0)()2k k Z π∈最小正周期π三、三角函数图像的平移变换和伸缩变换1. 由的图象得到()的图象x y sin =)sin(ϕω+=x A y 0,0A ω>>xy sin =方法一：先平移后伸缩方法二：先伸缩后平移操作向左平移φ个单位横坐标变为原来的倍1ω结果)sin(ϕ+=x y xy ωsin =操作横坐标变为原来的倍1ω向左平移个单位ϕω结果)sin(ϕω+=x y 操作纵坐标变为原来的A 倍结果)sin(ϕω+=x A y 注意：平移变换或伸缩变换都是针对自变量x 而言的，因此在用这样的变换法作图象时一定要注意平移与伸缩的先后顺序，否则会出现错误。

§5.1-3正弦函数的性质与图像（2课时）一、教学目标：1、知识与技能（1）回忆锐角的正弦函数定义；（2）熟练运用锐角正弦函数的性质；（3）理解通过单位圆引入任意角的正弦函数的意义；（4）掌握任意角的正弦函数的定义；（5）了解正弦函数图像的画法；（7）掌握五点作图法，并会用此方法画出[0，2π]上的正弦曲线。

2、过程与方法初中所学的正弦函数，是通过直角三角形中给出定义的；由于我们已将角推广到任意角的情况，而且一般都是把角放在平面直角坐标系中，这样一来，我们就在直角坐标系中来找直角三角形，从而引出单位圆；利用单位圆的独特性，是高中数学中的一种重要方法，在第二节课的正弦函数图像，以及在后面的正弦函数的性质中都有直接的应用；讲解例题，总结方法，巩固练习。

3、情感态度与价值观通过本节的学习，使同学们对正弦函数的概念有了一个新的认识；在由锐角的正弦函数推广到任意角的正弦函数的过程中，体会特殊与一般的关系，形成一种辩证统一的思想；通过单位圆的学习，建立数形结合的思想，激发学习的学习积极性；培养学生分析问题、解决问题的能力。

二、教学重、难点重点: 1.任意角的正弦函数定义，以及正弦函数值的几何表示。

2.正弦函数图像的画法。

3.正弦函数的性质 难点: 1.正弦函数值的几何表示。

2.利用正弦线画出y ＝sinx ，x∈[0， 2π]的图像。

第一课时§5.1从单位圆看正弦函数的性质§5.2 正弦函数的图像一、教学思路【创设情境，揭示课题】我们学习角的概念的推广和弧度制，就是为了学习三角函数。

请同学们回忆（1）角的概念的推广及弧度制、象限角等概念；（2）在单位圆中正弦函数是如何定义的？并想一想它有哪些性质？学生思考回答以后，教师小结。

【探究新知】一、在直角坐标系中，对于任意角R ∈α，在其终边上任取一点P(x,y)，则P 点到原点的距离22yx r +=, 定义角α的正弦ry=αs i n 如图1 在单位圆中，角的终边和单位圆的交点P 的坐标为（a,b ）,则sin α=b 如图2.可以看出正弦函数的下列性质：1、定义域是全体实数；2、值域是[]1,1-，其最大值是1，最小值是-1；3、是周期函数，其周期是2π；4、在[]π0,2上的单调性为：在⎥⎦⎤⎢⎣⎡2,0π，是增加的，在⎥⎦⎤⎢⎣⎡ππ，2上减少的；在⎥⎦⎤⎢⎣⎡23ππ，上是减少的；在⎥⎦⎤⎢⎣⎡ππ223，上是增加的. 二、用描点法画函数图像我们知道y ＝sinx 是周期函数，我们先画出在[]π0,2上的函数图像，在利用周期性将其延拓到整个定义域上，为此在[]π0,2上取一系列的x 值，列表，描点，再用光滑的曲线连接这些点，得到函数在区间[]π0,2的图像。

正弦函数的图象和性质以及三角函数的周期性编稿：孙永钊 审稿：王静伟【学习目标】1.能借助正弦线画出正弦函数的图象，并在此基础上由诱导公式画出余弦函数的图象.2.借助图象理解正弦函数的性质. 【要点梳理】要点一：正弦函数图象的画法 1．描点法：按照列表、描点、连线三步法作出正弦函数图象的方法。

2．几何法利用三角函数线作出正弦函数在]2,0[π内的图象，再通过平移得到x y sin =的图象。

3．五点法先描出正弦曲线的波峰、波谷和三个平衡位置这五个点，再利用光滑曲线把这五点连接起来，就得到正弦曲线在一个周期内的图象。

在确定正弦函数x y sin =在]2,0[π上的图象形状时，起关键作用的五个点是)0,2(),1,23(),0,(),1,2(),0,0(ππππ-要点诠释：（1）熟记正弦函数图象起关键作用的五点。

（2）若x R ∈，可先作出正弦函数在]2,0[π上的图象，然后通过左、右平移可得到x y sin =的图象。

要点二：正弦曲线（1）定义：正弦函数sin ()y x x R =∈的图象叫做正弦曲线。

（2）图象要点诠释：（1）由正弦曲线可以研究正弦函数的性质。

（2）运用数形结合的思想研究与正弦函数有关的问题，如[]0,2x π∈，方程lg sin x x =根的个数。

要点三：函数图象的变换图象变换就是以正弦函数的图象为基础通过对称、平移而得到。

sin sin()sin()y x y x y A x ϕωϕ=→=+→=+要点四：周期函数函数)(x f y =，定义域为I ，当I x ∈时，都有)()(x f T x f =+，其中T 是一个非零的常数，则)(x f y =是周期函数，T 是它的一个周期.要点诠释：1.定义是对I 中的每一个x 值来说的，只有个别的x 值满足)()(x f T x f =+或只差个别的x 值不满足)()(x f T x f =+都不能说T 是)(x f y =的一个周期.2.对于周期函数来说，如果所有的周期中存在一个最小的正数，就称它为最小正周期，三角函数中的周期一般都指最小正周期.要点五：正弦函数性质要点诠释：（1）正弦函数的值域为[]1,1-，是指整个正弦函数或一个周期内的正弦曲线，如果定义域不是全体实数，那么正弦函数的值域就可能不是[]1,1-，因而求正弦函数的值域时，要特别注意其定义域．（2）求正弦函数的单调区间时，易错点有二：一是单调区间容易求反，要注意增减区间的求法，如求sin()y x =-的单调递增区间时，应先将sin()y x =-变换为sin y x =-再求解，相当于求sin y x =的单调递减区间；二是根据单调性的定义，所求的单调区间必须在函数的定义域内，因此求单调区间时，必须先求定义域．要点六：正弦型函数sin()y A x ωϕ=+的性质．函数sin()y A x ωϕ=+与函数cos()y A x ωϕ=+可看作是由正弦函数sin y x =，余弦函数cos y x =复合而成的复合函数，因此它们的性质可由正弦函数sin y x =，余弦函数cos y x =类似地得到：（1）定义域：R （2）值域：[],A A -（3）单调区间：求形如sin()y A x ωϕ=+的函数的单调区间可以通过解不等式的方法去解答，即把x ωϕ+视为一个“整体”，分别与正弦函数sin y x =的单调递增（减）区间对应解出x ，即为所求的单调递增（减）区间．比如：由)(2222Z k k x k ∈+≤+≤-ππϕωππ解出x 的范围所得区间即为增区间，由)(23222Z k k x k ∈+≤+≤+ππϕωππ解出x 的范围，所得区间即为减区间． （4）奇偶性：正弦型函数sin()y A x ωϕ=+不一定具备奇偶性．对于函数sin()y A x ωϕ=+，当()k k z ϕπ=∈时为奇函数，当()2k k z πϕπ=±∈时为偶函数．要点诠释：判断函数sin()y A x ωϕ=+的奇偶性除利用定义和有关结论外，也可以通过图象直观判断，但不能忽视“定义域关于原点对称”这一前提条件．（5）周期：函数sin()y A x ωϕ=+的周期与解析式中自变量x 的系数有关，其周期为2T πω=．（6）对称轴和对称中心与正弦函数sin y x =比较可知，当()2x k k z πωϕπ+=±∈时，函数sin()y A x ωϕ=+取得最大值（或最小值），因此函数sin()y A x ωϕ=+的对称轴由()2x k k z πωϕπ+=±∈解出，其对称中心的横坐标()x k k z ωϕπ+=∈，即对称中心为,0()k k z πϕω-⎛⎫∈ ⎪⎝⎭．【典型例题】类型一：“五点法”作正弦函数的图象例1．用五点法作出函数2sin y x =-，[0,2]x π∈的图象. 【思路点拨】（1）取[0,2]π上五个关键的点（0，2）、（2π，1）、(,2)π、3(,3)2π、（2π，2）。