下载文档原格式
正弦函数图像和性质正弦函数是一种常见的函数，在数学研究中，它被广泛用于表达定义在实数集的函数的图像。
正弦函数可以通过其一般形式 y=sin x，其中x表示自变量，y表示函数值，也可以表示为极坐标形式 r=sin，其中θ表示极坐标参数，r表示正弦函数值，它也可以表示为复平面形式 z=sin(x+iy)，其中x表示实部，y表示虚部，z表示正弦函数结果，作为函数，正弦函数可以描述定义在实数集内的曲线。
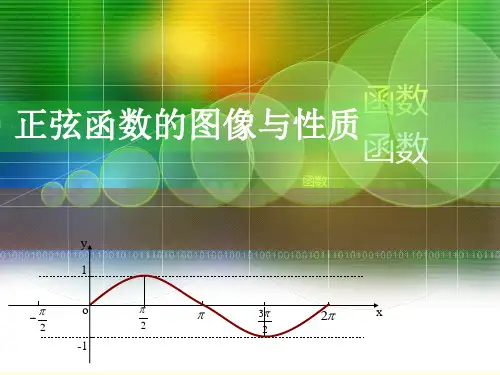
二、正弦函数图像正弦函数y=sin x的图像如下所示：图1弦函数y=sin x的图像可以看出，正弦函数的图像是一条以原点（0，0）为中心的周期性图像，它以（π，0）和（-π，0）为极点，它形似一个波浪，起伏不定，一个完整的周期长度为2π，其中π约等于3.1415926。
复平面正弦函数z=sin(x+iy)的图像如下所示：图2平面正弦函数z=sin(x+iy)的图像正弦函数的复平面图像的特点是：它形似旋转的空心圆，有一定的中心对称性，其图像可以看作是一个以原点为中心的旋转空心螺旋。
三、正弦函数的性质1、正弦函数的单调性在正弦函数曲线的一个周期内，函数值先递增，再递减，由此可以认为正弦函数是单调递减函数。
2、正弦函数的对称性正弦函数是对称函数，在一个周期内，函数值和其对称轴处的函数值相等，即sin(x) = sin(- x)，此外，在正弦函数曲线中，（π，0）和（-π，0）是函数的极值点，即sin(π) = sin(-π) = 0，此外，正弦函数也具有垂直对称性，可以表示为y=sin x的对称轴是x 轴，函数值的对称轴是y轴。
3、正弦函数的周期性正弦函数是一个周期函数，一个完整的周期长度为2π，由此，可以认为，当x在2π的整数倍的范围内，sin x的函数值和x在（0，2π）范围内的函数值是相同的。
4、正弦函数的极限性正弦函数的极限性可以用数学归纳法推导出来，即当x趋于正无穷大或负无穷大时，正弦函数的函数趋于1或-1，具体表示为lim x →∞sin x = 1；lim x→-∞sin x = -1。
1定义编辑数学术语正弦函数是三角函数的一种.定义与定理定义：对于任意一个实数x都对应着唯一的角（弧度制中等于这个实数），而这个角又对应着唯一确定的正弦值sin x，这样，对于任意一个实数x都有唯一确定的值sin x与它对应，按照这个对应法则所建立的函数，表示为f(x)=sin x，叫做正弦函数。
正弦函数的定理：在一个三角形中，各边和它所对角的正弦的比相等，即a/sin A=b/sin B=c/sin C 在直角三角形ABC中，∠C=90°，y为一条直角边，r为斜边，x为另一条直角边（在坐标系中，以此为底），则sin A=y/r,r=√（x^2+y^2）2性质编辑图像图像是波形图像（由单位圆投影到坐标系得出），叫做正弦曲线(sine curve)正弦函数x∈&定义域实数集R值域[-1，1] （正弦函数有界性的体现）最值和零点①最大值：当x=2kπ+（π/2），k∈Z时，y(max)=1②最小值：当x=2kπ+（3π/2），k∈Z时，y(min)=-1零值点：（kπ,0) ，k∈Z对称性既是轴对称图形，又是中心对称图形。
1）对称轴：关于直线x=（π/2）+kπ，k∈Z对称2）中心对称：关于点（kπ，0），k∈Z对称周期性最小正周期：y=sinx T=2π奇偶性奇函数（其图象关于原点对称）单调性在[-π/2+2kπ，π/2+2kπ]，k∈Z上是单调递增.在[π/2+2kπ，3π/2+2kπ]，k∈Z上是单调递减.3正弦型函数及其性质编辑正弦型函数解析式：y=Asin（ωx+φ）+h各常数值对函数图像的影响：φ（初相位）：决定波形与X轴位置关系或横向移动距离（左加右减）ω：决定周期（最小正周期T=2π/|ω|）A：决定峰值（即纵向拉伸压缩的倍数）h：表示波形在Y轴的位置关系或纵向移动距离（上加下减）作图方法运用“五点法”作图“五点作图法”即当ωx+φ分别取0，π/2，π，3π/2，2π时y的值.单位圆定义图像中给出了用弧度度量的某个公共角。
