正弦和余弦函数的图像及性质..
- 格式:ppt
- 大小:1.30 MB
- 文档页数:17
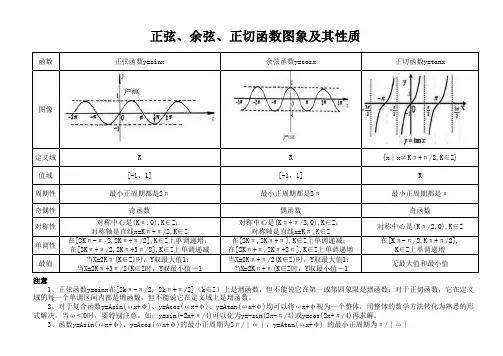
函数正弦函数y=sinx 余弦函数y=cosx 正切函数y=tanx图像定义域R R{x∣x≠Kπ+π/2,K∈Z}值域[-1,1][-1,1]R周期性最小正周期都是2π最小正周期都是2π最小正周期都是π奇偶性奇函数偶函数奇函数对称性对称中心是(Kπ,0),K∈Z;对称轴是直线x=Kπ+π/2,K∈Z对称中心是(Kπ+π/2,0),K∈Z;对称轴是直线x=Kπ,K∈Z对称中心是(Kπ/2,0),K∈Z单调性在[2Kπ-π/2,2Kπ+π/2],K∈Z上单调递增;在[2Kπ+π/2,2Kπ+3π/2],K∈Z上单调递减在[2Kπ,2Kπ+π],K∈Z上单调递减;在[2Kπ+π,2Kπ+2π],K∈Z上单调递增在[Kπ-π/2,Kπ+π/2],K∈Z上单调递增最值当X=2Kπ(K∈Z)时,Y取最大值1;当X=2Kπ+3π/2(K∈Z时,Y取最小值-1当X=2Kπ+π/2(K∈Z)时,Y取最大值1;当X=2Kπ+π(K∈Z时,Y取最小值-1无最大值和最小值正弦、余弦、正切函数图象及其性质注意1、正弦函数y=sinx在[2kπ-π/2, 2kπ+π/2](k∈Z)上是增函数,但不能说它在第一或第四象限是增函数;对于正切函数,它在定义域的每一个单调区间内都是增函数,但不能说它在定义域上是增函数。
2、对于复合函数y=Asin(ωx+φ)、y=Acos(ωx+φ)、y=Atan(ωx+φ)均可以将ωx+φ视为一个整体,用整体的数学方法转化为熟悉的形式解决。
当ω<0时,要特别注意。
如:y=sin(-2x+π/4)可以化为y=-sin(2x-π/4)或y=cos(2x+π/4)再求解。
3、函数y=Asin(ωx+φ)、y=Acos(ωx+φ)的最小正周期为2π/∣ω∣,y=Atan(ωx+φ) 的最小正周期为π/∣ω∣。









6.1 正弦函数和余弦函数的图像与性质
1.定义
型如sin (x R)y x =∈的函数叫做正弦函数.
型如cos (x R)y x =∈的函数叫做余弦函数.
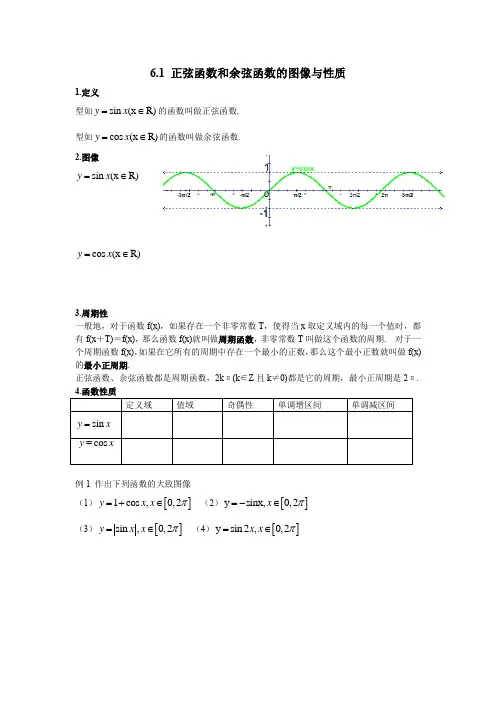
2.图像
sin (x R)y x =∈
cos (x R)y x =∈
3.周期性
一般地,对于函数f(x),如果存在一个非零常数T ,使得当x 取定义域内的每一个值时,都有f(x +T)=f(x),那么函数f(x)就叫做周期函数,非零常数T 叫做这个函数的周期. 对于一个周期函数f(x),如果在它所有的周期中存在一个最小的正数,那么这个最小正数就叫做f(x)的最小正周期.
正弦函数、余弦函数都是周期函数,2k π(k ∈Z 且k ≠0)都是它的周期,最小正周期是2π.
例1 作出下列函数的大致图像
(1)[]1cos ,0,2y x x π=+∈ (2)[]y sinx,0,2x π=-∈
(3)[]sin ,0,2y x x π=∈ (4)[]y sin 2,0,2x x π=∈
例2.求下列函数的定义域与值域
(1)1sin 22y x =
(2)y
例3.求函数2sin 33y x π⎛
⎫=-+ ⎪⎝⎭
的最大值与最小值,并求使其取得最大值、最小值的x 的集合
例4.矩形ABCD 的四个顶点分别在矩形A ’B ’C ’D ’的四条边上,AB=a ,BC=b ,如果AB 与A ’B ’的夹角为α,那么当α为和值时,矩形A ’B ’C ’D ’的周长最大?。