下载文档原格式
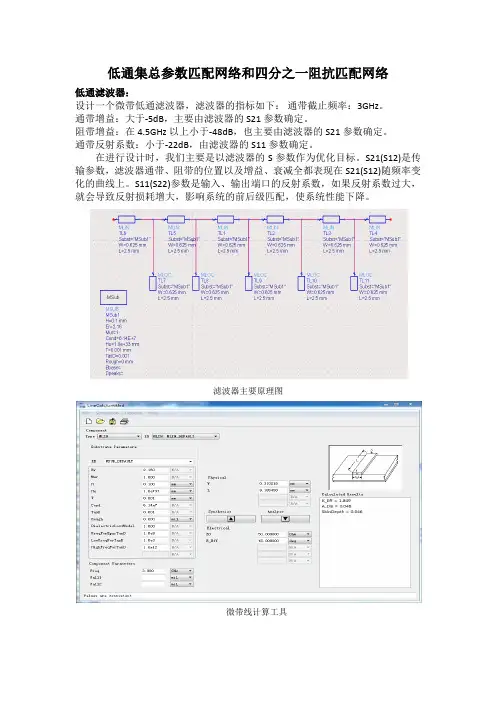
低通集总参数匹配网络和四分之一阻抗匹配网络
低通滤波器：
设计一个微带低通滤波器，滤波器的指标如下：通带截止频率：3GHz。
通带增益：大于-5dB，主要由滤波器的S21参数确定。
阻带增益：在4.5GHz以上小于-48dB，也主要由滤波器的S21参数确定。
通带反射系数：小于-22dB，由滤波器的S11参数确定。
在进行设计时，我们主要是以滤波器的S参数作为优化目标。
S21(S12)是传输参数，滤波器通带、阻带的位置以及增益、衰减全都表现在S21(S12)随频率变化的曲线上。
S11(S22)参数是输入、输出端口的反射系数，如果反射系数过大，就会导致反射损耗增大，影响系统的前后级匹配，使系统性能下降。
滤波器主要原理图
微带线计算工具
设置完变量的原理图
变量设置窗口
微带低通滤波器原理图
S参数仿真电路设置
S21参数曲线图
S11参数曲线图四分之一阻抗匹配网络：。
实验四 阻抗匹配网络理论一、 实验目的1． 了解基本的阻抗匹配理论；2． 利用实验模组实际测量以了解匹配电路的特性。
二、 实验原理在高频电路设计中，阻抗匹配是很重要的一环。
从直流电路的基本理论中，我们知道若信号源的电阻与输出之负载电阻相同时，就可在输出端得到最大的功率输出。
但是在交流电路中，除了电阻，尚有电容与电感等电抗性组件，因此若要求得到最大功率输出时，除了两端的电阻相等外，还需信号源的电抗与负载的电抗互成共轭才行。
所以阻抗匹配的目的就是经由适当方法选择组件使得信号源与负载两端的电抗值成共轭关系，以便产生谐振而互相抵消，使得电路中仅存电阻性，而能得到最大功率传输。
其次，由于现成的网络组件，其阻抗值会随着频率的变化而变化，因此阻抗匹配只能适用于某一特定的频率，但是对于宽频的电路来说，所设计的电路都期望能涵盖整个频宽。
就理论而言，可借着适当方法来增加阻抗匹配的频宽范围。
如图7-1（a ）所示：输入信号经过传输以后，其输出功率与输入功率之间存在以下关系，信号的输出功率直接决定于输入阻抗与输出阻抗之比。
inout S S in SL LL S S L P k kP R V P R k R R R R V R I Pout ⋅+=⇒=⋅=⋅+=⋅=22222)1()(图7-1（a ） 输出输入功率关系图输出功率与阻抗比例的关系图见图7-1（b ）。
由图可知，当R L =R S 时可获得最大输出功率，此时为阻抗匹配状态。
图7-1（b）输出功率与阻抗比例关系图推而广之，如图7-1（c）所示，当输入阻抗Z S与负载阻抗Z L间成为Z S=Z L*的关系时，满足广义阻抗匹配的条件。
所以，阻抗匹配电路也可以称为阻抗变换器。
当Z L=Z S*,即是[匹配]图7-1(c) 广义[阻抗匹配]关系图欲得到最大的功率输出，则须对电路加以阻抗匹配，阻抗匹配网络一般可分为三种：L 型、π型及T 型三种。
选用何种匹配端视情况而定，除非有特别需求，一般都是以最少的零件来完成匹配。
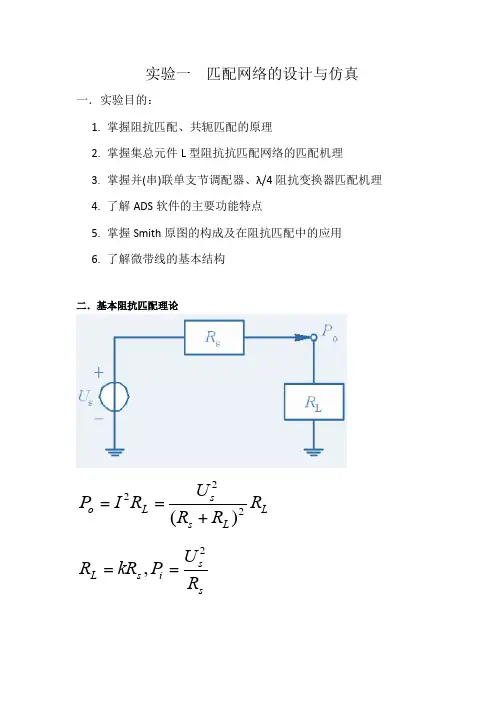
实验一匹配网络的设计与仿真一．实验目的：1. 掌握阻抗匹配、共轭匹配的原理2. 掌握集总元件L 型阻抗抗匹配网络的匹配机理3. 掌握并(串)联单支节调配器、λ/4阻抗变换器匹配机理4. 了解ADS 软件的主要功能特点5. 掌握Smith 原图的构成及在阻抗匹配中的应用6. 了解微带线的基本结构二．基本阻抗匹配理论L L s s L o R R R U R I P 222)(+==s s i s L R U P kR R 2,==信号源的输出功率取决于U s 、R s 和R L 。
在信号源给定的情况下，输出功率取决于负载电阻与信号源内阻之比k 。
当R L =R s 时可获得最大输出功率，此时为阻抗匹配状态。
无论负载电阻大于还是小于信号源内阻，都不可能使负载获得最大功率，且两个电阻值偏差越大，输出功率越小。
1. 共轭匹配：当时，源输出功率最大，称作共轭匹配。
2. 阻抗匹配：λ/4阻抗变换器i o P k k P 2)1(+=*g LZ Z=三、ADS仿真步骤1.打开ADS2.新建一个Workspace，并命名为“学号或姓名”3.新建原理图4.原理图设计界面4.在元件面板列表中选择“Simulating-S Param”，单击和放两个Term和一个S-P控件5.接下来接续设置各个器件的参数6.执行菜单命令【Tools】 【Smith Chart】，弹出“SmartComponent Sync”对话框；选择“Update SmartComponent from Smith Chart Utility”，单击“OK”7.单击“DefineSource/Load Network terminations”按钮8.采用LC分立器件匹配过程如下图所示9.改变L、C 的位置，观察L、C值变化时输入阻抗的变化轨迹单击“Build ADS Circuit”按钮，即可生成相应的电路选中DA_SmithChartMatch控件，单击“”，以查看匹配电路单击“”，返回原理图单击“”图标，进行仿真单击“”，在结果窗口单击，就会出现如下对话框，仿真结果图形输出。
阻抗匹配设计原理及⽅法阻抗匹配（Impedance matching）是微波电⼦学⾥的⼀部分，主要⽤于传输线上，来达⾄所有⾼频的微波信号皆能传⾄负载点的⽬的，⼏乎不会有信号反射回来源点，从⽽提升能源效益。
阻抗匹配有两种，⼀种是透过改变阻抗⼒（lumped-circuit matching），另⼀种则是调整传输线的波长（transmission line matching）。
要匹配⼀组线路，⾸先把负载点的阻抗值，除以传输线的特性阻抗值来归⼀化，然后把数值划在史密斯图上。
改变阻抗⼒把电容或电感与负载串联起来，即可增加或减少负载的阻抗值，在图表上的点会沿着代表实数电阻的圆圈⾛动。
如果把电容或电感接地，⾸先图表上的点会以图中⼼旋转180度，然后才沿电阻圈⾛动，再沿中⼼旋转180度。
重复以上⽅法直⾄电阻值变成1，即可直接把阻抗⼒变为零完成匹配。
阻抗匹配：简单的说就是「特性阻抗」等于「负载阻抗」。
调整传输线由负载点⾄来源点加长传输线，在图表上的圆点会沿着图中⼼以逆时针⽅向⾛动，直⾄⾛到电阻值为1的圆圈上，即可加电容或电感把阻抗⼒调整为零，完成匹配。
阻抗匹配则传输功率⼤，对于⼀个电源来讲，单它的内阻等于负载时，输出功率最⼤，此时阻抗匹配。
最⼤功率传输定理，如果是⾼频的话，就是⽆反射波。
对于普通的宽频放⼤器，输出阻抗50Ω，功率传输电路中需要考虑阻抗匹配，可是如果信号波长远远⼤于电缆长度，即缆长可以忽略的话，就⽆须考虑阻抗匹配了。
阻抗匹配是指在能量传输时,要求负载阻抗要和传输线的特征阻抗相等,此时的传输不会产⽣反射,这表明所有能量都被负载吸收了.反之则在传输中有能量损失。
⾼速PCB布线时，为了防⽌信号的反射，要求是线路的阻抗为50欧姆。
这是个⼤约的数字,⼀般规定同轴电缆基带50欧姆,频带75欧姆,对绞线则为100欧姆,只是取个整⽽已,为了匹配⽅便.阻抗从字⾯上看就与电阻不⼀样，其中只有⼀个阻字是相同的，⽽另⼀个抗字呢？简单地说，阻抗就是电阻加电抗，所以才叫阻抗；周延⼀点地说，阻抗就是电阻、电容抗及电感抗在向量上的和。
用LC 元件设计L 型的阻抗匹配网络一 设计要求：用分立LC 设计一个L 型阻抗匹配网络，使阻抗为Z s =25-j*15 Ohm 的信号源与阻抗为Z L =100-j*25 Ohm 的负载匹配，频率为50Mhz 。
（L 节匹配网络） 二 阻抗匹配的原理用两个电抗元件设计L 型的匹配网络，应该是匹配网络设计中最简单的一种， 但仅适用于较小的频率和电路尺寸的范围，即L 型的匹配网络有其局限性 在RF 理论中，微波电路和系统的设计（包括天线，雷达等），不管是无源电路还是有源电路，都必须考虑他们的阻抗匹配（impedance matching ）问题。
阻抗匹配网络是设计微波电路和系统时采用最多的电路元件。
其根本原因是微波电路传输的是电磁波，不匹配会引起严重的反射，致使严重损耗。
所以在设计时，设计一个好的阻抗匹配网络是非常重要的。
阻抗匹配是指负载阻抗与激励源内部阻抗互相适配，得到最大功率输出的一种工作状态。
对于不同特性的电路，匹配条件是不一样的。
在纯电阻电路中，当负载电阻等于激励源内阻时，则输出功率为最大，这种工作状态称为匹配，否则称为失配。
根据最大功率传输定理，要获得信号源端到负载端的最大传输功率，需要满足信号源阻抗与负载阻抗互为共轭的条件，即L L S S iX R iX R +=+。
若电路为纯电阻电路则0==L S X X ，即L S R R =。
而此定理表现在高频电路上，则是表示无反射波，即反射系数为0.值得注意的是，要得到最佳效率的能量传输并不需要负载匹配，此条件只是避免能量从负载端到信号源端形成反射的必要条件。
当RL=Rs 时可获得最大输出功率,此时为阻抗匹配状态。
无论负载电阻大于还是小于信号源内阻,都不可能使负载获得最大功率,且两个电阻值偏差越大,输出功率越小. 阻抗匹配是无线电技术中常见的一种工作状态，它反映了输人电路与输出电路之间的功率传输关系。
当电路实现阻抗匹配时，将获得最大的功率传输。
阻抗匹配及应用设计实战（老外的经典诠释）阻抗匹配是指信号源或者传输线跟负载之间的一种合适的搭配方式。
阻抗匹配分为低频和高频两种情况讨论。
我们先从直流电压源驱动一个负载入手。
由于实际的电压源，总是有内阻的（请参看输出阻抗一问），我们可以把一个实际电压源，等效成一个理想的电压源跟一个电阻r串联的模型。
假设负载电阻为R，电源电动势为U，内阻为r，那么我们可以计算出流过电阻R的电流为：I=U/(R+r)，可以看出，负载电阻R越小，则输出电流越大。
负载R上的电压为：Uo=IR=U/[1+(r/R)]，可以看出，负载电阻R越大，则输出电压Uo越高。
再来计算一下电阻R消耗的功率为：P=I*I*R=[U/(R+r)]*[U/(R+r)]*R=U*U*R/(R*R+2*R*r+r*r)=U*U*R/[(R-r)*(R-r)+4*R*r]=U*U/{[(R-r)*(R-r)/R]+4*r}对于一个给定的信号源，其内阻r是固定的，而负载电阻R则是由我们来选择的。
注意式中[(R-r)*(R-r)/R]，当R=r时，[(R-r)*(R-r)/R]可取得最小值0，这时负载电阻R上可获得最大输出功率Pmax=U*U/(4*r)。
即，当负载电阻跟信号源内阻相等时，负载可获得最大输出功率，这就是我们常说的阻抗匹配之一。
对于纯电阻电路，此结论同样适用于低频电路及高频电路。
当交流电路中含有容性或感性阻抗时，结论有所改变，就是需要信号源与负载阻抗的的实部相等，虚部互为相反数，这叫做共厄匹配。
在低频电路中，我们一般不考虑传输线的匹配问题，只考虑信号源跟负载之间的情况，因为低频信号的波长相对于传输线来说很长，传输线可以看成是“短线”，反射可以不考虑（可以这么理解：因为线短，即使反射回来，跟原信号还是一样的）。
从以上分析我们可以得出结论：如果我们需要输出电流大，则选择小的负载R；如果我们需要输出电压大，则选择大的负载R；如果我们需要输出功率最大，则选择跟信号源内阻匹配的电阻R。
最全的阻抗匹配与史密斯（Smith）圆图基本原理摘要：本文利用史密斯圆图作为RF阻抗匹配的设计指南。
文中给出了反射系数、阻抗和导纳的作图范例，并给出了MAX2472工作在900MHz时匹配网络的作图范例。
事实证明，史密斯圆图仍然是确定传输线阻抗的基本工具。
在处理RF系统的实际应用问题时，总会遇到一些非常困难的工作，对各部分级联电路的不同阻抗进行匹配就是其中之一。
一般情况下，需要进行匹配的电路包括天线与低噪声放大器(LNA)之间的匹配、功率放大器输出(RFOUT)与天线之间的匹配、LNA/VCO输出与混频器输入之间的匹配。
匹配的目的是为了保证信号或能量有效地从“信号源”传送到“负载”。
在高频端，寄生元件(比如连线上的电感、板层之间的电容和导体的电阻)对匹配网络具有明显的、不可预知的影响。
频率在数十兆赫兹以上时，理论计算和仿真已经远远不能满足要求，为了得到适当的最终结果，还必须考虑在实验室中进行的RF测试、并进行适当调谐。
需要用计算值确定电路的结构类型和相应的目标元件值。
有很多种阻抗匹配的方法，包括•计算机仿真：由于这类软件是为不同功能设计的而不只是用于阻抗匹配，所以使用起来比较复杂。
设计者必须熟悉用正确的格式输入众多的数据。
设计人员还需要具有从大量的输出结果中找到有用数据的技能。
另外，除非计算机是专门为这个用途制造的，否则电路仿真软件不可能预装在计算机上。
•手工计算：这是一种极其繁琐的方法，因为需要用到较长(“几公里”)的计算公式、并且被处理的数据多为复数。
•经验：只有在RF领域工作过多年的人才能使用这种方法。
总之，它只适合于资深的专家。
•史密斯圆图：本文要重点讨论的内容。
本文的主要目的是复习史密斯圆图的结构和背景知识，并且总结它在实际中的应用方法。
讨论的主题包括参数的实际范例，比如找出匹配网络元件的数值。
当然，史密斯圆图不仅能够为我们找出最大功率传输的匹配网络，还能帮助设计者优化噪声系数，确定品质因数的影响以及进行稳定性分析。
阻抗匹配电路原理及应用阻抗匹配（impedance matching）信号源内阻与所接传输线的特性阻抗大小相等且相位一样，或传输线的特性阻抗与所接负载阻抗的大小相等且相位一样，分别称为传输线的输入端或输出端处于阻抗匹配状态，简称为阻抗匹配。
否则，便称为阻抗失配。
有时也直接叫做匹配或失配。
阻抗匹配是指信号源或者传输线跟负载之间的一种合适的搭配方式。
阻抗匹配分为低频和高频两种情况讨论。
我们先从直流电压源驱动一个负载入手。
由于实际的电压源，总是有内阻的，我们可以把一个实际电压源，等效成一个理想的电压源跟一个电阻r串联的模型。
假设负载电阻为R，电源电动势为U，内阻为r，那么我们可以计算出流过电阻R的电流为：I=U/（R+r），可以看出，负载电阻R越小，则输出电流越大。
负载R上的电压为：Uo=IR=U/［1+（r/R）］，可以看出，负载电阻R越大，则输出电压Uo越高。
再来计算一下电阻R消耗的功率为：P=I2×R=［U/（R+r）］2×R=U2×R/（R2+2×R×r+r2）=U2×R/［（R-r）2+4×R×r］=U2/{［（R-r）2/R］+4×r}对于一个给定的信号源，其内阻r是固定的，而负载电阻R则是由我们来选择的。
注意式中［（R-r）2/R］，当R=r 时，［（R-r）2/R］可取得最小值0，这时负载电阻R上可获得最大输出功率Pmax=U2/（4×r）。
即，当负载电阻跟信号源内阻相等时，负载可获得最大输出功率，这就是我们常说的阻抗匹配之一。
此结论同样适用于低频电路及高频电路。
当交流电路中含有容性或感性阻抗时，结论有所改变，就是需要信号源与负载阻抗的的实部相等，虚部互为相反数，这叫做共扼匹配。
在低频电路中，我们一般不考虑传输线的匹配问题，只考虑信号源跟负载之间的情况，因为低频信号的波长相对于传输线来说很长，传输线可以看成是“短线”，反射可以不考虑（可以这么理解：因为线短，即使反射回来，跟原信号还是一样的）。
