混合式π型阻抗匹配网络设计
- 格式:pdf
- 大小:102.12 KB
- 文档页数:6
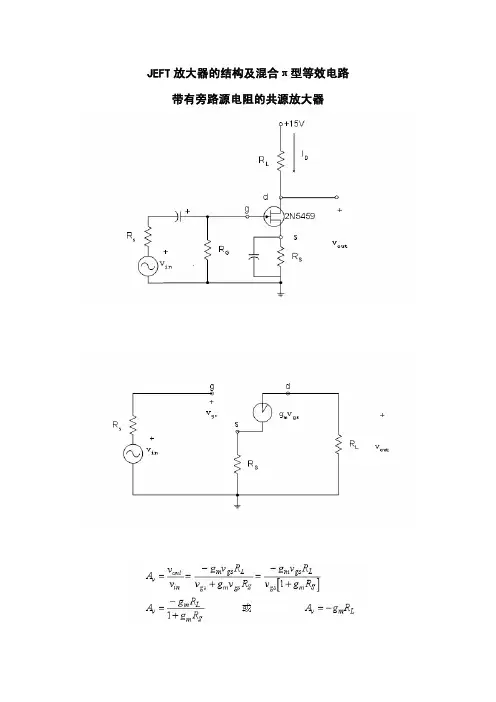
带有旁路源电阻的共源放大器带有旁路源电阻的共源放大器FET 共源放大器的偏置图示方法1. 找出电路中的V GS(OFF) & I DSS ;用曲线描摹仪测量[V GS(OFF) = V P = 栅源电压当V GS =0时,HICH I D = 0,I DSS = I D ] 2. 假设R S << R L3. 在输出特性图上画出负载线。
保持R S << R L 在图页上截取;也就是避开附近的垂直负载线4. 由负载线截距计算R L ,用最接近的标准值5. 挑出输出最大线性输出范围的Q 点V GS 值6. 计算21:⎟⎟⎠⎞⎜⎜⎝⎛−=P GSDSS D D VV I I I ;或从特性曲线中估算 7. 计算R S 用V GS 除以I D 。
⎟⎟⎠⎞⎜⎜⎝⎛=D GS I V S R 。
用最接近的标准值8. 比较R S 和 R L ;如果R S 和R L 接近,重画负载线9. 重新计算新V GS 下的R S ;如果需要的话,重复步骤7和步骤8!计算JEFT的小信号g m1. 由从曲线描摹仪得到的漏极特性曲线上的∆I D 和∆V GS 计算g m = ∆I D/∆V GS [大信号g m ]2. 或使用MEDIAN 特性表的值[用于快速估计]3. 或⎟⎟⎠⎞⎜⎜⎝⎛−−=P GS PDSS m VV V I g 12 其中V GS 为工作点的值。
V P = V GS(OFF) ; I DSS = I D @ V GS = 0.注意这是小信号 跨导取决于静态工作点,与三极管的情况相似FET 源随器负载线/增益例子和方法1. 求得电路中的V GS(OFF) & I DSS ;用曲线描摹仪的测量。
[V GS(OFF) = V P = 栅源电压,当V GS =0时,I D = 0,I DSS = I D ] 2. 选择Q 点;也就是从漏极特性图上选择V GS3. 计算21:⎟⎟⎠⎞⎜⎜⎝⎛−=P GSDSS D D VV I I I ;或由特性图估计 4. 计算R S ;使用最接近的标准值5. 计算负载线截距,[因为I D -V DS = 0,截距可能与图页有很大距离,所以可能要使用∆]6. 计算g m :⎟⎟⎠⎞⎜⎜⎝⎛−−=P GS PDSS m VV V I g 12 7. 计算A V :Sm Sm V R g R g A +=18.S mO R g R //1=9. 例 [V P = V GS(OFF) = -5.8V; I DSS = 9mA]。
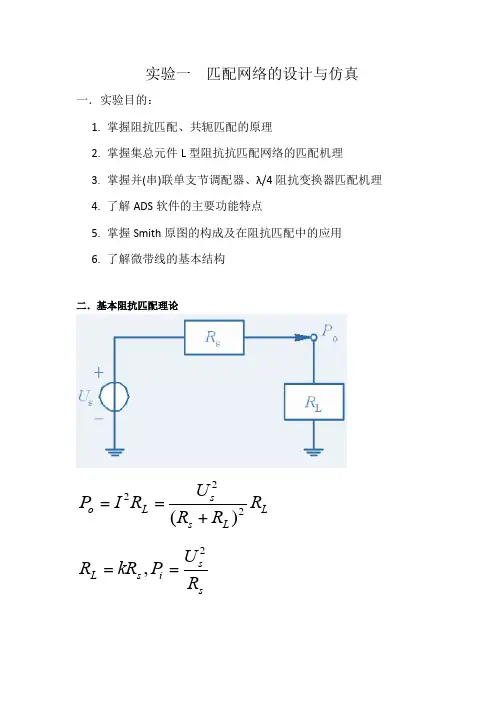
实验一匹配网络的设计与仿真一.实验目的:1. 掌握阻抗匹配、共轭匹配的原理2. 掌握集总元件L 型阻抗抗匹配网络的匹配机理3. 掌握并(串)联单支节调配器、λ/4阻抗变换器匹配机理4. 了解ADS 软件的主要功能特点5. 掌握Smith 原图的构成及在阻抗匹配中的应用6. 了解微带线的基本结构二.基本阻抗匹配理论L L s s L o R R R U R I P 222)(+==s s i s L R U P kR R 2,==信号源的输出功率取决于U s 、R s 和R L 。
在信号源给定的情况下,输出功率取决于负载电阻与信号源内阻之比k 。
当R L =R s 时可获得最大输出功率,此时为阻抗匹配状态。
无论负载电阻大于还是小于信号源内阻,都不可能使负载获得最大功率,且两个电阻值偏差越大,输出功率越小。
1. 共轭匹配:当时,源输出功率最大,称作共轭匹配。
2. 阻抗匹配:λ/4阻抗变换器i o P k k P 2)1(+=*g LZ Z=三、ADS仿真步骤1.打开ADS2.新建一个Workspace,并命名为“学号或姓名”3.新建原理图4.原理图设计界面4.在元件面板列表中选择“Simulating-S Param”,单击和放两个Term和一个S-P控件5.接下来接续设置各个器件的参数6.执行菜单命令【Tools】 【Smith Chart】,弹出“SmartComponent Sync”对话框;选择“Update SmartComponent from Smith Chart Utility”,单击“OK”7.单击“DefineSource/Load Network terminations”按钮8.采用LC分立器件匹配过程如下图所示9.改变L、C 的位置,观察L、C值变化时输入阻抗的变化轨迹单击“Build ADS Circuit”按钮,即可生成相应的电路选中DA_SmithChartMatch控件,单击“”,以查看匹配电路单击“”,返回原理图单击“”图标,进行仿真单击“”,在结果窗口单击,就会出现如下对话框,仿真结果图形输出。

阻抗匹配设计原理及⽅法阻抗匹配(Impedance matching)是微波电⼦学⾥的⼀部分,主要⽤于传输线上,来达⾄所有⾼频的微波信号皆能传⾄负载点的⽬的,⼏乎不会有信号反射回来源点,从⽽提升能源效益。
阻抗匹配有两种,⼀种是透过改变阻抗⼒(lumped-circuit matching),另⼀种则是调整传输线的波长(transmission line matching)。
要匹配⼀组线路,⾸先把负载点的阻抗值,除以传输线的特性阻抗值来归⼀化,然后把数值划在史密斯图上。
改变阻抗⼒把电容或电感与负载串联起来,即可增加或减少负载的阻抗值,在图表上的点会沿着代表实数电阻的圆圈⾛动。
如果把电容或电感接地,⾸先图表上的点会以图中⼼旋转180度,然后才沿电阻圈⾛动,再沿中⼼旋转180度。
重复以上⽅法直⾄电阻值变成1,即可直接把阻抗⼒变为零完成匹配。
阻抗匹配:简单的说就是「特性阻抗」等于「负载阻抗」。
调整传输线由负载点⾄来源点加长传输线,在图表上的圆点会沿着图中⼼以逆时针⽅向⾛动,直⾄⾛到电阻值为1的圆圈上,即可加电容或电感把阻抗⼒调整为零,完成匹配。
阻抗匹配则传输功率⼤,对于⼀个电源来讲,单它的内阻等于负载时,输出功率最⼤,此时阻抗匹配。
最⼤功率传输定理,如果是⾼频的话,就是⽆反射波。
对于普通的宽频放⼤器,输出阻抗50Ω,功率传输电路中需要考虑阻抗匹配,可是如果信号波长远远⼤于电缆长度,即缆长可以忽略的话,就⽆须考虑阻抗匹配了。
阻抗匹配是指在能量传输时,要求负载阻抗要和传输线的特征阻抗相等,此时的传输不会产⽣反射,这表明所有能量都被负载吸收了.反之则在传输中有能量损失。
⾼速PCB布线时,为了防⽌信号的反射,要求是线路的阻抗为50欧姆。
这是个⼤约的数字,⼀般规定同轴电缆基带50欧姆,频带75欧姆,对绞线则为100欧姆,只是取个整⽽已,为了匹配⽅便.阻抗从字⾯上看就与电阻不⼀样,其中只有⼀个阻字是相同的,⽽另⼀个抗字呢?简单地说,阻抗就是电阻加电抗,所以才叫阻抗;周延⼀点地说,阻抗就是电阻、电容抗及电感抗在向量上的和。

pi型匹配天线原理
PI型匹配天线是一种常见的天线匹配网络,用于调节天线的输
入阻抗,使其与传输线或射频电路的输出阻抗匹配。
其原理涉及天
线的输入阻抗匹配和频率选择两个方面。
首先,让我们来看天线的输入阻抗匹配原理。
PI型匹配网络通
常由两个电感元件和一个电容元件组成,形状类似于字母"π"。
这
种结构可以有效地调节天线的输入阻抗,使其与传输线或射频电路
的输出阻抗相匹配。
通过调节电感元件和电容元件的数值,可以实
现对天线输入阻抗的精确调节,从而最大限度地提高能量传输效率。
其次,PI型匹配天线还可以用于频率选择。
通过精心设计电感
元件和电容元件的数值,可以使PI型匹配网络在特定的频率范围内
表现出理想的阻抗匹配特性。
这使得PI型匹配天线在特定频段内具
有较好的性能表现,例如在无线通信系统中,可以实现对特定频率
信号的有效接收和发射。
除了上述原理外,还有一些其他方面需要考虑。
例如,PI型匹
配天线的设计需要考虑天线的物理结构、工作频率范围、功率传输
要求等因素。
此外,天线的周围环境和相邻元件也会对PI型匹配网
络的性能产生影响,因此在实际设计中需要综合考虑多种因素。
总的来说,PI型匹配天线通过精心设计的电感和电容元件,可以实现天线的输入阻抗匹配和频率选择,从而提高天线的性能和效率。
在无线通信系统和射频电路设计中,PI型匹配天线起着非常重要的作用,是一种常见且有效的天线匹配网络。


混合∏型等效电路混合型等效电路是指由电阻、电感、电容和电压源、电流源组成的电路,其中既有串联的元件,也有并联的元件。
这种电路可以通过等效变换转化为纯电阻电路或纯电感电路或纯电容电路,方便分析和计算。
1. 等效变换混合型电路中,可以通过等效变换将电路转化为纯电阻电路、纯电感电路或纯电容电路。
具体的等效变换如下:(1)串联电阻和并联电阻的等效变换将串联电阻和并联电阻的等效变换公式列出,即:串联电阻:$R_{eq}=R_1+R_2+...+R_n$并联电阻:$\frac{1}{R_{eq}}=\frac{1}{R_1}+\frac{1}{R_2}+...+\frac{1}{R_n}$(2)串联电感和并联电感的等效变换将串联电感和并联电感的等效变换公式列出,即:串联电感:$L_{eq}=L_1+L_2+...+L_n$并联电感:$\frac{1}{L_{eq}}=\frac{1}{L_1}+\frac{1}{L_2}+...+\frac{1}{L_n}$ (3)串联电容和并联电容的等效变换将串联电容和并联电容的等效变换公式列出,即:串联电容:$\frac{1}{C_{eq}}=\frac{1}{C_1}+\frac{1}{C_2}+...+\frac{1}{C_n}$ 并联电容:$C_{eq}=C_1+C_2+...+C_n$(4)电感和电容的等效变换将电感和电容的等效变换公式列出,即:电感:$L=\frac{1}{\omega^2C}$电容:$C=\frac{1}{\omega^2L}$其中,$\omega$为角频率。
2. 混合型等效电路的分析混合型等效电路的分析可以采用基尔霍夫定律、欧姆定律、电压分压定律、电流分流定律等方法进行计算。
具体的分析步骤如下:(1)将电路转化为纯电阻电路、纯电感电路或纯电容电路。
(2)根据基尔霍夫定律列出方程组,求解电路中各元件的电流和电压。
(3)利用欧姆定律计算电路中各元件的电流和电压。

图1是大家所熟知的作为高频阻抗匹配电路的π形匹配电路。
通过改变可变电容C1和C2的容量比,能够从RS<RL到RS>RL进行自由匹配。
另外,由于具有低通滤波器的构成,还具有除去高频波的能力。
图1 π形阻抗匹配电路的构成
举一个例子,如果要求fo=5MHz、RS=50Ω、RL=1kΩ时的各个常数,则
照片1是L=7μH、C1=750pF、C2=170pF时的输入阻抗-频率特性。
该特性在负载短路时和断开时有很大的不同。
这和先前阐述的π形滤波器相同,断开时表示串联共振现象,阻抗下降到1Ω左右。
照片 1 π形阻抗匹配电路…由负载电阻RL的变化而引起的输人阻抗的变化(fo=5MHz,RL=0及∞,f=1M~lOOMHz)
照片2是扩大测定共振频率附近的波形。
在RL=1kΩ处变成宽频带的特性。
照片3不是测定输人阻抗ZIN,而是测定R±jX中的阻抗R成分。
在RL=∞时R成分很大,不能向负载送人电力。
另外,在RL=0时R成分在1Ω以下(z中几乎都是电抗成分),仍然会产生不匹配。
在RL=1kΩ处,即被认为凡的频率处,约62Ω(计算值为50Ω),即使频率变化很大也不会产生大幅的变化。
π形匹配电路由于是阻抗匹配电路,所以其特征是可进行从+jx(电感性)到一jx(电容性)的匹配。
线圈L使用抽头式可变电感器,电容C1、C2,使用空气可变电容。
照片2 π形阻抗匹配电路…由负载电阻RL变化而引起的输人阻抗的变化(fo=5MHz,Rl=0及∞,f=4M~6MHz,线性跨度)
照片3 π形阻抗匹配电路的输人电阻R的变化(fo=5MHz,RL=0及∞,f=4M~6MHz,线性跨度)。

阻抗匹配计算公式阻抗匹配是电路设计中的重要概念,它是指在电路中使用适当的元件和电路拓扑配置,以实现输入和输出之间的最大功率传输。
阻抗匹配旨在消除电路之间的反射和干涉,从而提高电路的效率和传输质量。
阻抗匹配的基本原则是将电路的输入和输出阻抗匹配到同一个数值,从而实现最大功率转移。
在通信系统中,常常需要将信源的输出阻抗与传输线的输入阻抗匹配,以确保信号的准确传输和最小的反射损耗。
在电路中,阻抗可以看作是交流电路中的电阻。
阻抗的计算通常需要考虑电感和电容的影响。
以下是常见的阻抗匹配计算公式:1.并联匹配公式:对于并联匹配,常用公式是通过将输入阻抗与输出阻抗求倒数并求和得到:1/Zin = 1/Zs + 1/Zl其中,Zin是输入阻抗,Zs是信源阻抗,Zl是负载阻抗。
2.串联匹配公式:对于串联匹配,常用公式是通过将输入阻抗与输出阻抗求和得到:Zin = Zs + Zl其中,Zin是输入阻抗,Zs是信源阻抗,Zl是负载阻抗。
3.阻抗变换公式:阻抗变换是一种常见的阻抗匹配技术,通过变换阻抗的数值和形式,实现输入和输出阻抗之间的匹配。
常用的阻抗变换公式包括:a.L型匹配网络:Zin = j*Xl + (Zs*Zl)^0.5其中,Xl是电感值。
b.T型匹配网络:Zin = Zs*Zl / (Zs + Zl)c.π型匹配网络:Zin = (Zs*Zl) / (Zs + Zl)4.变压器匹配公式:变压器匹配是一种常用的阻抗匹配技术,通过变换信号源和负载阻抗的转化比,实现输入和输出之间的阻抗匹配。
常用的变压器匹配公式包括:Np/Ns=(Zl/Zs)^0.5其中,Np是一次侧匝数,Ns是二次侧匝数,Zl是负载阻抗,Zs是信源阻抗。
以上只是阻抗匹配计算中常用的一些公式,实际的阻抗匹配计算可能还需要考虑其他因素,如频率响应、功率传输等。
在实际应用中,可以根据具体的电路要求和条件选择合适的阻抗匹配方案和公式,以实现最佳的匹配效果。

实验三 阻抗匹配网络的设计与仿真一、实验设计目标1、设计目标:设计微带单枝短截线匹配电路,把阻抗Ohm j Z L )50*30(+=的负载匹配到阻抗Ohm j Z s )40*55(-=的信号源,中心频率为1.5GHz2、设计目标:设计L 型阻抗匹配网络,使Ohm j Z s )15*25(-=信号源与Ohm j Z L )25*100(-=的负载匹配,频率为50MHz二、实验设备1、台式电脑 1台 配置要符合相关软件要求2、ADS 软件 1套 微波软件三、实验过程及仿真结果1、新建工程和设计原理图如图1所示。
设置仿真参数,进行仿真,仿真结果如图2所示。
2、分立电容电感匹配在频率不是很高的应用场合,可以使用分立电容电感器件进行不同阻抗之间的匹配,如果频率不高,分立器件的寄生参数对整体性能的影响可以忽略。
用分立电容电感进行匹配设计的步骤如下:(1)在原理图中设定输入输出端口和相应的阻抗(2)在原理图里加入Smith Chart Matching 控件,并设置相关的频率和输入输出阻抗等参数(3)打开Smith Chart Utility ,倒入对应Smith Chart Matching 控件的相关参数或者输入相关参数(4)Smith Chart Utility 中选用器件完成匹配(5)生成匹配的原理图。
四、实验过程及仿真结果设计1的实验原理图图1,设计1的等效电路图图2,设计1的Smith 图形图3,设计1的仿真图形图4,设计2的实验原理图图5,设计2的等效电路图图6,设计2的Smith 图形图7,设计2的仿真图形图8。
五、实验体会本次实验让我了解了阻抗匹配网络的设计与仿真。
我感觉自己懂得还是很少,不过经过这两次实验自己不断摸索,发现并学会了很多的关于射频电路设计方面的东西,我感觉自己对这方面兴趣挺大的,不过要准备考研,这学期的课都没有好好上,也是一种遗憾,射频这方面的学习也只能学到这种很模糊的状态了,如果以后还接触的话,我一定好好学。

∏型阻抗匹配电路
∏型阻抗匹配电路是一种常见的电路配置,用于将一个电路的
输出阻抗与另一个电路的输入阻抗进行匹配。
它由三个电阻连接在一起,形成一个字母“∏”的形状。
∏型阻抗匹配电路的工作原理如下:当信号通过第一个电阻
R1进入电路时,一部分信号会被分配到两个并联的电阻R2和R3上。
因为R2和R3是并联的,它们的等效阻抗会小于R1
的阻抗。
这样,一部分电流会流过R2和R3,而另一部分电
流会继续通过R1。
通过调节R2和R3的阻值,可以实现输入和输出阻抗的匹配。
当R2和R3的阻值合适时,输入阻抗和输出阻抗的阻抗匹配
最佳,信号传输效率最高。
∏型阻抗匹配电路常用于射频和微波电路中,以实现信号传输
的最大功率传输。
它可以用于匹配信号发生器和功率放大器之间的阻抗,或者用于匹配天线和收发器之间的阻抗。
需要注意的是,∏型阻抗匹配电路的设计需要根据具体的电路
要求和特性进行选择和调整。
不同的电路参数可能需要不同的阻抗匹配电路配置。

电子设计中的阻抗匹配技术
在电子设计领域中,阻抗匹配技术是一项非常重要的技术。
阻抗匹配是指将信号源、传输介质和负载之间的阻抗调整到最佳匹配状态,以最大限度地传输信号能量,减小信号反射和降低功耗。
阻抗匹配技术主要应用于无线通信系统、射频电路、微波电路以及其他高频电路设计中。
在这些系统中,往往需要将不同阻抗的元件连接在一起,因此需要进行阻抗匹配来确保信号的正常传输和工作效率。
阻抗匹配技术的一种常见方法是通过使用阻抗转换网络来实现。
阻抗转换网络可以将不匹配的阻抗转换为匹配的阻抗,从而提高信号传输效果。
常见的阻抗转换网络有匹配变压器、L型匹配网络、π型匹配网络等。
另一种常见的阻抗匹配技术是使用阻抗匹配电路,包括电阻、电容、电感等元件来调整阻抗,以实现信号源、传输线和负载之间的阻抗匹配。
这种方法通常可以在电路板设计中方便地实现。
除了阻抗匹配技术,还有一种被广泛应用的技术是阻抗匹配网络的设计。
通过使用软件仿真工具和网络分析仪器,工程师可以精确地设计阻抗匹配网络,以满足特定的阻抗要求。
这种方法可以在设计阶段提前解决阻抗匹配的问题,提高整体设计的准确性和效率。
总的来说,阻抗匹配技术在电子设计中起着至关重要的作用,能够确保信号的正常传输和系统的高效性能。
工程师在设计高频电路时,需要充分了解阻抗匹配的原理和方法,灵活运用各种技术手段,以实现电路的稳定性和可靠性。
只有保证阻抗匹配的准确性,才能使电子系统发挥出最佳的性能和效果。
阻抗匹配网络的设计与制作一、 实验目的1. 了解如何使用史密斯图来设计阻抗匹配网络;2. 了解了解电容抽头与电感抽头匹配网络设计原理;3. 了解宽带匹配网络设计原理。
二、 设计原理阻抗交换器的设计方法,根据使用元件及工作频率高低,大致可分为无源元件型和传输线型两种。
(一) 无源元件型此种电路是利用电感及电容来设计。
根据工作频宽的大小,基本上可分为L 型、T 型及П型等三种。
我们仅以T 型网络为例。
T 型匹配电路(以R S < R L 为例)步骤一:决定工作频率fc 、负载Q 值、输入阻抗R S 及输出阻抗R L 。
并求出R small = MIN( R S ,R L )。
步骤二:依图8-1(a )中所示及下列公式计算出X S1、X P1、X P2及X S2 。
图8-1 (a) T 型匹配电路211(1),,small S S P R R R Q X Q R X Q=⋅+=⋅=L S P LR Q X Q R X R R Q ⋅==-=22222,,1步骤三:根据电路选用元件的不同,可有四种形式。
如图8-1(b )(c )(d )(e )所示。
其中电感及电容值之求法,如下所列:2CXL f π=12C C f Xπ=⋅(b ) (c )(d ) (e )图8-1 (b)、(c)、(d)、(e) T 型匹配电路(二) 传输线型在传统的电子电路设计中,因为其操作频率不高,亦即是信号之波长远大于电路板上传输线之长度,所以于设计上我们可以不考虑讯号在传输在线传输时起点与终端的差异。
然而随着工作频率的上升,信号之波长将不再远大于电路板上传输线之长度,而会接近传输线结构的倍数,所以传统的电路理论无法有效的说明其电压与电流变化的关系以及电压与电流与位置之间的关系。
传输线理论即在阐述电压与电流及位置间的关系,令电压与电流在位置z时为V (z ) 与 I (z ) ,当电波行进一段距离 z + Δz 后,电压与电流分别产生 V (z + Δz ) 、I (z + Δz ) 的变化。
混合∏型等效电路
混合型等效电路是一种模拟电路,它通常由模拟和数字电路组成。
混合型等效电路的特点是可以在数字和模拟电路之间提供桥梁。
在混合型等效电路中,数字和模拟信号可以相互转换。
混合型等效电路可以用于各种应用,例如通信、仪器、控制系统和嵌入式系统。
在通信中,混合型等效电路可以用于模拟信号的数字化和数字信号的模拟化。
在仪器中,混合型等效电路可以用于信号采集、信号处理和控制。
在嵌入式系统中,混合型等效电路可以用于数字信号的处理和输出。
混合型等效电路的设计需要考虑到数字和模拟电路之间的接口。
接口的设计需要考虑到信号的转换、精度、速度和功耗等因素。
另外,混合型等效电路的设计还需要考虑到电路的可靠性、稳定性和成本等方面。
总之,混合型等效电路是一种非常有用的电路设计方法。
它可以在数字和模拟电路之间提供桥梁,同时具有广泛的应用领域。
- 1 -。
阻抗匹配及调配⽹络参数设计2019-08-29摘要:在信息传输系统中,不论是超⾼频、⾼频还是低频,阻抗匹配都是⼀个极为重要的环节。
为了能使能量得到有效地传输,使负载得到最⼤的有效功率,⽂中给出了阻抗匹配的⽅法及⽹络计算公式,同时给出了抑制射频倒送的主要⽅法。
关键词:阻抗匹配;⽹络参数;射频倒送;信息传输中图分类号:TN92 ⽂献标识码:A⽂章编号:2095-1302(2011)10-0072-02Design of Impedance Matching and Deployment of Network ParametersLI Jun-xue1, LI Zhan-yu2(1.Shaanxi People′s Broadcasting Station, Xi’an 710068, China; 2 Xi’an Jiaotong University, Xi’an 710049, China) Abstract: In the information transmission system, whether it is ultra-high frequency, high frequency or low frequency, impedance matching is an extremely important part. In order to enable the effective transmission of energy, and to maximize the effective power of load, methods of impedance matching and formulas of network computation are proposed, and the inhibition of RF down the main method of delivery is provided.Keywords: impedance matching; network parameters; RF send down; information transmission0 引⾔所谓阻抗匹配,⼀般来说,就是任意⼀负载通过⼀个特殊的⽹络,都应将其转换为某设备或电路所要求的特定阻抗,以使其获得最⼤的能量,从⽽达到最佳的传输效果。
Pi型,L型匹配L形和PI匹配网络(zz)2010-03-21 08:43L形和PI匹配网络(zz)2009-02-23 23:23L形匹配网络要实现最大的功率传输,必须使使负载阻抗和源阻抗之间相匹配。
而实现这个匹配的通常做法是在源和负载之间插入一个无源网络。
这种无源网络通常被视为匹配网络。
事实上,它们的功能不仅仅限于为实现理想功率传输而在源和负载之间进行阻抗匹配,还有很多其他功能,比如减小噪声干扰、提高功率容量和提高频率响应的线性度等。
通常我们认为,匹配网络的用途就是实现阻抗变换,就是将给定的阻抗值变换成其它更合适的阻抗值。
在本章中我们将要讨论的主要内容就是利用无源匹配网络进行阻抗变换的技术,重点是确保在源和负载之间形成最小反射。
我们将Smith圆图作为主要设计工具。
下面的2个实际例子是工作中经常会碰到2种匹配网络,即形。
例题2.1:已知晶体管在2GHz频率点的输出阻抗是。
请设计一个如图2.1所示的L形匹配网络,使输入阻抗为的天线能够得到最大功率。
假定特性阻抗。
图2.1 发射机与天线之间的匹配网络解:信号源与负载之间实现最大功率传输的条件是信号源阻抗与负载阻抗共轭相等。
1)计算发射机和天线的归一化阻抗。
zt=Zt/Zo=2+j1za=Za/Zo=1+j0.2由于与发射机连接的第一个元件为并联电容,则并联后的总阻抗应与zt落在阻抗-导纳复合Smith圆图中的同一等电导圆上。
如图2.2所示。
2)再将一个电感串联在电容与发射机zt并联后的总电阻上。
最终的串联阻抗将沿着等电阻圆移动。
要实现最大功率传输,则发射机的输出匹配网络的输出阻抗必须等于天线阻抗的共轭复数。
因此,此等电阻圆必须经过zm=za*=1-j0.2点。
3)找到Smith圆图中两个圆的交点。
此交点就是发射机与电容并联后的总归一化阻抗。
从Smith圆图中我们可以看到,这个点的归一化阻抗值约为ztc=1-j1.22,相应的归一化导纳值约为ytc=0.4+j0.49。
阻抗匹配电路原理及应用阻抗匹配(impedance matching)信号源内阻与所接传输线的特性阻抗大小相等且相位一样,或传输线的特性阻抗与所接负载阻抗的大小相等且相位一样,分别称为传输线的输入端或输出端处于阻抗匹配状态,简称为阻抗匹配。
否则,便称为阻抗失配。
有时也直接叫做匹配或失配。
阻抗匹配是指信号源或者传输线跟负载之间的一种合适的搭配方式。
阻抗匹配分为低频和高频两种情况讨论。
我们先从直流电压源驱动一个负载入手。
由于实际的电压源,总是有内阻的,我们可以把一个实际电压源,等效成一个理想的电压源跟一个电阻r串联的模型。
假设负载电阻为R,电源电动势为U,内阻为r,那么我们可以计算出流过电阻R的电流为:I=U/(R+r),可以看出,负载电阻R越小,则输出电流越大。
负载R上的电压为:Uo=IR=U/[1+(r/R)],可以看出,负载电阻R越大,则输出电压Uo越高。
再来计算一下电阻R消耗的功率为:P=I2×R=[U/(R+r)]2×R=U2×R/(R2+2×R×r+r2)=U2×R/[(R-r)2+4×R×r]=U2/{[(R-r)2/R]+4×r}对于一个给定的信号源,其内阻r是固定的,而负载电阻R则是由我们来选择的。
注意式中[(R-r)2/R],当R=r 时,[(R-r)2/R]可取得最小值0,这时负载电阻R上可获得最大输出功率Pmax=U2/(4×r)。
即,当负载电阻跟信号源内阻相等时,负载可获得最大输出功率,这就是我们常说的阻抗匹配之一。
此结论同样适用于低频电路及高频电路。
当交流电路中含有容性或感性阻抗时,结论有所改变,就是需要信号源与负载阻抗的的实部相等,虚部互为相反数,这叫做共扼匹配。
在低频电路中,我们一般不考虑传输线的匹配问题,只考虑信号源跟负载之间的情况,因为低频信号的波长相对于传输线来说很长,传输线可以看成是“短线”,反射可以不考虑(可以这么理解:因为线短,即使反射回来,跟原信号还是一样的)。
实验四 阻抗匹配网络理论一、 实验目的1. 了解基本的阻抗匹配理论;2. 利用实验模组实际测量以了解匹配电路的特性。
二、 实验原理在高频电路设计中,阻抗匹配是很重要的一环。
从直流电路的基本理论中,我们知道若信号源的电阻与输出之负载电阻相同时,就可在输出端得到最大的功率输出。
但是在交流电路中,除了电阻,尚有电容与电感等电抗性组件,因此若要求得到最大功率输出时,除了两端的电阻相等外,还需信号源的电抗与负载的电抗互成共轭才行。
所以阻抗匹配的目的就是经由适当方法选择组件使得信号源与负载两端的电抗值成共轭关系,以便产生谐振而互相抵消,使得电路中仅存电阻性,而能得到最大功率传输。
其次,由于现成的网络组件,其阻抗值会随着频率的变化而变化,因此阻抗匹配只能适用于某一特定的频率,但是对于宽频的电路来说,所设计的电路都期望能涵盖整个频宽。
就理论而言,可借着适当方法来增加阻抗匹配的频宽范围。
如图7-1(a )所示:输入信号经过传输以后,其输出功率与输入功率之间存在以下关系,信号的输出功率直接决定于输入阻抗与输出阻抗之比。
inout S S in SL LL S S L P k kP R V P R k R R R R V R I Pout ⋅+=⇒=⋅=⋅+=⋅=22222)1()(图7-1(a ) 输出输入功率关系图输出功率与阻抗比例的关系图见图7-1(b )。
由图可知,当R L =R S 时可获得最大输出功率,此时为阻抗匹配状态。
图7-1(b)输出功率与阻抗比例关系图推而广之,如图7-1(c)所示,当输入阻抗Z S与负载阻抗Z L间成为Z S=Z L*的关系时,满足广义阻抗匹配的条件。
所以,阻抗匹配电路也可以称为阻抗变换器。
当Z L=Z S*,即是[匹配]图7-1(c) 广义[阻抗匹配]关系图欲得到最大的功率输出,则须对电路加以阻抗匹配,阻抗匹配网络一般可分为三种:L 型、π型及T 型三种。
选用何种匹配端视情况而定,除非有特别需求,一般都是以最少的零件来完成匹配。