大学物理之运动学60页PPT

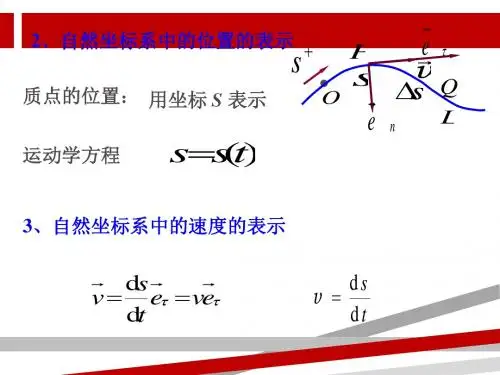
用自然坐标表示 s s(t )
2. 轨道方程
从运动方程中消去时间t，得到 的x，y，z 之间的关系式。
S0
法
向
P
n轴
切向轴 11
五、位移
描述质点在空间位置变化的物理量。
1.定义 从起点指向终点的有向线段
大小： 起点指向终点 间的直线距离
方向： 起点
终点
r r2 r1
z
起 点
A ( x1, y1, z1)
法
n
向 轴
P S的正负号： 轨迹上O点起沿哪个方
向测量的。
切向轴
10
四、运动方程与轨道方程
表示位置随时间变 化的函数式。
1. 运动方程
x x(t ) z p(x, y, z)
用直角坐标表示 y y(t )
用位矢表示
z
r r(t)
z(t)
ok
xi
r
j
y
x(t)i y(t) j z(t)k S 0 o
x2 y2 z2
r与z轴夹角为
方向： cos x cos y cos z
r
r
r
9
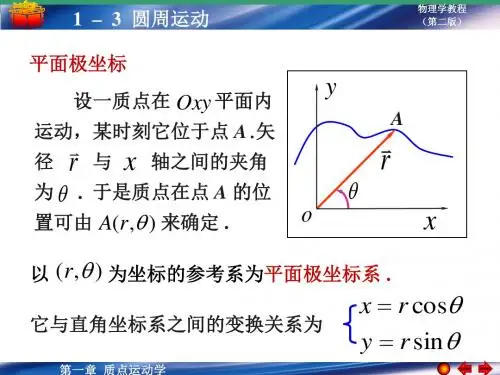
平面运动
r
x2 y2
r xi yj
tg
y
x
直线运动 r xi
y
jo
p(
r
i
x,
y)
x
r p( x)
o
x
3. 自然法
S0
P 表示质点与原点间的
S的绝对值： 曲线长度。
o
表示这个曲线距离是从 S 0
方向：切线方向，并指向前进方向
v
dr
dx
i
dy
j

2
匀速圆周运动的实例分析
3
2024/1/29
13
圆周运动
2024/1/29
01
变速圆周运动
02
变速圆周运动的特点和性质
03
变速圆周运动的实例分析
14
相对运动
2024/1/29
01 02 03
参考系与坐标系 参考系的选择和建立 坐标系的种类和应用
15
相对运动
2024/1/29
相对速度与牵连速度 相对速度的定义和计算
2024/1/29
简谐振动的动力学特征
分析简谐振动的动力学特征，包括回复力、加速度 、速度、位移等物理量的变化规律。
简谐振动的能量特征
讨论简谐振动的能量特征，包括动能、势能 、总能量等的变化规律，以及能量转换的过 程。
32
振动的合成与分解
2024/1/29
同方向同频率简谐振动的合成
分析两个同方向同频率简谐振动的合成规律，介绍合振动振幅、合 振动相位等概念。
5
大学物理的研究方法
03
观察和实验
建立理想模型
数学方法
物理学是一门以实验为基础的自然科学， 观察和实验是物理学的基本研究方法，通 过实验可以验证物理假说和理论，发现新 的物理现象和规律。
理想模型是物理学中经常采用的一种研究 方法，它忽略了次要因素，突出了主要因 素，使物理问题得到简化。
数学是物理学的重要工具，通过数学方法 可以精确地描述物理现象和规律，推导物 理公式和定理。
2024/1/29
适用范围
适用于一切自然现象，包括力学、热学、电磁学 、光学等各个领域。
应用举例
热力学第一定律、机械能守恒定律、爱因斯坦的 质能方程等。

日心系
z
地面系
o
y
x 地心系
★ 注意： 参考系不一定是静止的！
14
第13页/共63页
§2 质点运动的描述 一、位置矢量和位移矢量 二、 速度矢量 三、加速度矢量 四、其他物理量
15
第14页/共63页
一、位置矢量（位矢） 描写质点空间位置的物理量
位置矢量：由原点向质点所在位置作的
z
有向线段
轨道
r
方向： cos x r , cos y r , cos z r 16
第15页/共63页
二、运动方程
为简单只讨论平面运动的情况
1.
质点的运动方程 — 原则上写做 r
位矢随时间的函数关系。
r (t)
★ 直角坐标系中：
(1) 矢量式
r (t) x(t) i y(t) j
(2) 分量式
x x(t) y y(t)
1. 质点（实际研究对象的简化，理想模型 ） — 没有大小和形状、只具有质量的点。
可以将物体简化为质点的两种情况：
(1) 物体本身的线度和它活动的范围相比小得很多（此时物体 的形变及转动显得并不重要）。
(2) 物体不形变，不作转动（此时任意时刻物体上各点的速度 及加速度 都相同，其任一点的运动可以代表物体所有点 的运动）。
位移 Δr 是矢量，有大小和方向：
大小： Δr
Δx2 Δy2
Δr 方向： tan y
x
(
为 r 与
x
轴的夹角）
19
第18页/共63页
位 矢 大 小 的 增量 位移
★ 注意：
1. Δ r 与Δ r 的区别
⑴Δr
是标量，Δ
r

碰撞后两物体粘在一起以 共同速度运动的碰撞。此 时机械能损失最大，动能
之和最小。
05
流体力学基础
流体的性质与分类
流体的定义
流体是指在外力作用下，能够连续变形且不能恢复原 来形状的物质。
流体的性质
流动性、压缩性、黏性。
流体的分类
按物理性质可分为气体和液体；按化学性质可分为纯 净物和混合物。
流体静力学
重力势能
重力做功与路径无关，只与初末 位置的高度差有关。 03
机械能守恒定律
04 只有重力或弹力做功的物体系统 内，动能与势能可以相互转化， 而总的机械能保持不变。
刚体定轴转动动力学
刚体定轴转动的描述
角速度、角加速度和转动惯量等物理量的定义和 计算。
刚体定轴转动的动能定理
刚体定轴转动时，合外力矩对刚体所做的功等于 刚体转动动能的变化。
弹性势能与动能之间的转化
在振动过程中，物体的动能和弹性势能不断相互转化。
弹性碰撞与非弹性碰撞
弹性碰撞
碰撞过程中，物体间无机 械能损失的碰撞。碰撞后 两物体以相同的速度分开
，且动能之和不变。
非弹性碰撞
碰撞过程中，物体间有机 械能损失的碰撞。碰撞后 两物体以不同的速度分开
，且动能之和减小。
完全非弹性碰撞
伯努利方程的应用
伯努利方程在流体力学中有广泛的应用，如计算管道中流体的流速和流量、分析机翼升力原理、解释 喷雾器工作原理等。同时，伯努利方程也是一些工程领域（如水利工程、航空航天工程等）中设计和 分析的重要依据。
06
分析力学基础
约束与自由度
约束的概念
约束是对物体运动的一种限制，它减少了物体的自 由度。
牛顿运动定律
牛顿第一定律（惯性定律）

t 0
最新课件
31
a、切向加速度
aa t ldtid m v0 t0; vtdd vtv 0 lti mv 0ddt20 2svt00
dv dt
0
b、法向加速度
an
an
ldtit d vm tn00 vtn; vdd ltiv mnn 0v v 最tv新 课dd件ns0n dd0 stvn0ddtvn20dds
a
dv车 dt
v02h2
3
(s2 h2)2
最新课件
27
1.2.2 曲线运动的描述
1、平面曲线运动的直角坐标系描述—以抛体运动为例
1）物 体a v 0 作 抛常 0 体运动量 的运且 动学a 与 条v 件0 夹 ： 角 0 0
2）重力场中抛体运动的描述
(1)速度公式
vx v0 cos vy v0 sin gt
13
3）运动方程和轨道方程
a、质点在运动过程中，空间位置随时间变化的函数式称为运 动方程。
表示为： x x ( t), y y ( t), z z ( t). 或 rr(t)
运动方程是时间t的显函数。
b、质点在空间所经过的路径称为轨道（轨迹）。 从上式中消去t即可得到轨道方程。 轨道方程不是时间t显函数。
t 4 0 4
最新课件
23
(4) v dr 3 i(t3 ) jm s 1
则
dt v43i7j
m
s1
(5)
∵
v 0 3 i 3 j,v 4 3 i 7 j
∴ a v v 4 v 0 4 j 1 j
t 4 4
(6) adv1jms2
dt
m s 2
这说明该点只有 方向的加速度，且为恒量。

9
加速度
z
v
v2
1、平均加速度
速度的增量与所用时间的比 值叫做质点的平均加速度
v1
a v v2 v1
O
y
t t2 t1
2、瞬时加速度
定义：平均加速度的极限值称 为瞬时加速度，简称加速度
lim a
t0
v t
dv dt
d 2r dt2
r
x
ax
a y
a
z
dvx dt
dvy dt
dvz dt
v
v
lim AB
v
ds
v2
t0 t R t0 t R dt R
an=v2/R，法向加速度，指向圆心。
28
a
一般的圆周运动中的速度和加速度：
r 为常数
r 0 r 0
速度
v rrˆ rˆ rˆ
加速度
a (r r2 )rˆ (2r r)ˆ
r2rˆ rˆ
v r a v2 rˆ dv ˆ
r2
r1
x
(
x2i
＋y2
j
z2k
)
(
x1i ＋y1
j
z1
k)
( x2 x1 )i ( y2 y1 ) j (z2 z1 )k
•位移与路程的区别 位移是矢量：是指位置矢量的变化 路程是标量：是指运动轨迹的长度
z
r1
P1 r r2 P2
O
y
8
速度
1、平均速度 v r r2 r1 t t2 t1
v u v 速度合成
V：绝对速度 V’：相对速度 u：牵连速度
加速度的相对性
dv du dv dt dt dt

刚体的特点
刚体具有无限多的自由度，其运动状态完全 由其质心位置和相对于质心的角速度决定。
刚体的平动和转动
平动
刚体的平动是指刚体在运动过程中，其质心 沿某一确定直线作匀速或变速直线运动，同 时刚体上任意一点都跟随质心以相同的方式 运动。
转动
刚体的转动是指刚体在运动过程中，其上任 意一点都绕着某一定点作圆周运动，而该定
伽利略变换定理
当两个参考系之间的相对速度恒定时，时间和空间的 关系是线性的，即变换是线性的。
相对运动的应用实例
交通工具的运动
在交通工具上观察到的运动，如 汽车、火车、飞机等，都是相对 运动的应用实例。
天体运动
天体之间的运动，如行星绕太阳 旋转、卫星绕行星旋转等，也是 相对运动的应用实例。
THANK YOU
= frac{Delta v}{Delta t}$。这些公式和定理是描述匀加速直线运动规律的基础。
匀加速直线运动的应用实例
总结词
匀加速直线运动在日常生活和工程领域中有着广泛的 应用，如汽车的启动和制动、物体的自由落体等。
详细描述
匀加速直线运动的应用实例很多。在交通领域，汽车的 启动和制动可以视为匀加速直线运动，加速度的大小影 响汽车的启动和制动时间。在航空航天领域，火箭的发 射和卫星的变轨也可以视为匀加速直线运动，通过控制 加速度的大小和方向可以改变火箭或卫星的运动轨迹。 此外，自由落体也是匀加速直线运动的一种表现形式， 地球上的物体在忽略空气阻力的情况下自由下落时，可 以视为做匀加速直线运动。
位移和速度
位移描述
位移是物体位置的变化量，用矢量表示，有大小和方向。
速度定义
速度是描述物体运动快慢的物理量，等于位移与时间的比值 。

▪Leabharlann 29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人，倚靠在明眼的跛子肩上。——叔本华
谢谢！
62
▪
26、要使整个人生都过得舒适、愉快，这是不可能的，因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情，化为上进的力量，才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者，好之者不如乐之者。——孔子
大物 01运动学
•
6、黄金时代是在我们的前面，而不在 我们的 后面。
•
7、心急吃不了热汤圆。
•
8、你可以很有个性，但某些时候请收 敛。
•
9、只为成功找方法，不为失败找借口 (蹩脚 的工人 总是说 工具不 好)。
•
10、只要下定决心克服恐惧，便几乎 能克服 任何恐 惧。因 为，请 记住， 除了在 脑海中 ，恐惧 无处藏 身。-- 戴尔． 卡耐基 。

2
y
a
an
v

a
e
大小 a
a n 方向 θ tan a
1
a a
2
2 n
o
A e n
x
切向加速度(速度大小变化) 法向加速度(速度方向变化)
dv a e d t2 v an en r
利用自然坐标, 一切运动可以 根据切向、法向加速度来分类：
a
an
角量与线量的关系 v 速度与角速度的关系
s d θ v r r ω lim t d t t 0
v 加速度与角速度和角加速度的关系
s r
s P r
o
Q

x (极轴 )
vr ad d t

v 2 a v r n r
2
例1一质点作半径为0.1m 的圆周运动，已知运动学方程为
2 4 t( r a d )
3
求 (1) t = 2s 时，质点的切向加速度和法向加速度的大小; (2) t = 2s 时，质点的加速度。 解 (1)由运动学方程可得角速度和角加速度
d d 3 2 ( 2 4) t 1 2 t d t d t d d 2 ( 1 2 t ) 2 4 t d t d t
依据材料概括晚清中国交通方式的特点，并分析其成因。
提示：特点：新旧交通工具并存(或：传统的帆船、独轮车， 近代的小火轮、火车同时使用)。 原因：近代西方列强的侵略加剧了中国的贫困，阻碍社会发 展；西方工业文明的冲击与示范；中国民族工业的兴起与发展；
政府及各阶层人士的提倡与推动。
[串点成面· 握全局]
2 2 4
任意时刻，质点的切向加速度和法向加速度的大小

令 y 0 ，可得飞行时间： 令 v y 0 , 可得上升高度： 把飞行时间代入 x 得射程：
g
x
2v0 sin T g 2 v0 sin 2 H ymax 2g 2 v0 sin 2 s g
抛体运动的矢量描述
y
v0 t
1 2 gt 2
dv g dt

2
2 sin sin cos( ) cos( ) 2 sin cos sin( ) sin( ) 2 cos cos cos( ) cos( ) sin 2 2 sin cos sin 2 2 cos 2 1 2 sin 2 2 cos2 1 cos2 2
如何正确理解瞬时速率？ dr ds
r dr ds v v lim t 0 t dt dt
3.加速度 平均加速度
v (t )
v (t +Δ t)
v a t
瞬时加速度
r(t)
r (t +Δ t )
o
2 v d v d r a lim 2（m s 2） t 0 t d t dt
v0 v i cos
并非收绳速度的投影
2. 极坐标系 ( r , ) ( er , e )
r rer
d er d e dt dt d e d er dt dt
o

e
r
er
P(r , )
dr d er dr d v er r er r e dt dt dt dt 2 d r dr d er d e d d d a 2 er r r e dt dt dt dt dt dt dt