单纯形解法与对偶解法

应⽤运筹学基础：线性规划（4）-对偶与对偶单纯形法这⼀节课讲解了线性规划的对偶问题及其性质。

引⼊对偶问题考虑⼀个线性规划问题：$$\begin{matrix}\max\limits_x & 4x_1 + 3x_2 \\ \text{s.t.} & 2x_1 + 3x_2 \le 24 \\ & 5x_1 + 2x_2 \le 26 \\ & x \ge0\end{matrix}$$ 我们可以把这个问题看作⼀个⽣产模型：⼀份产品 A 可以获利 4 单位价格，⽣产⼀份需要 2 单位原料 C 和 5 单位原料 D；⼀份产品 B 可以获利 3 单位价格，⽣产⼀份需要 3 单位原料 C 和 2 单位原料 D。

现有 24 单位原料 C，26 单位原料 D，问如何分配⽣产⽅式才能让获利最⼤。

但假如现在我们不⽣产产品，⽽是要把原料都卖掉。

设 1 单位原料 C 的价格为 $y_1$，1 单位原料 D 的价格为 $y_2$，每种原料制定怎样的价格才合理呢？⾸先，原料的价格应该不低于产出的产品价格（不然还不如⾃⼰⽣产...），所以我们有如下限制：$$2y_1 + 5y_2 \ge 4 \\ 3y_1 + 2y_2 \ge3$$ 当然也不能漫天要价（也要保护消费者利益嘛- -），所以我们制定如下⽬标函数：$$\min_y \quad 24y_1 + 26y_2$$ 合起来就是下⾯这个线性规划问题：$$\begin{matrix} \min\limits_y & 24y_1 + 26y_2 \\ \text{s.t.} & 2y_1 + 5y_2 \ge 4 \\ & 3y_1 + 2y_2 \ge 3 \\ & y \ge 0\end{matrix}$$ 这个问题就是原问题的对偶问题。

对偶问题对于⼀个线性规划问题（称为原问题，primal，记为 P） $$\begin{matrix} \max\limits_x & c^Tx \\ \text{s.t.} & Ax \le b \\ & x \ge 0\end{matrix}$$ 我们定义它的对偶问题（dual，记为 D）为 $$\begin{matrix} \min\limits_x & b^Ty \\ \text{s.t.} & A^Ty \ge c \\ & y \ge 0\end{matrix}$$ 这⾥的对偶变量 $y$，可以看作是对原问题的每个限制，都⽤⼀个变量来表⽰。

1.单纯形法某工厂生产产品Ⅰ，Ⅱ。

生产单位产品所需台时为2台时和1台时，使用台时限额是40台时，生产单位产品使用的原材料分别是1Kg 和3Kg ，原材料的总限额是30Kg,单位产品的利润分别是3元和4元。

求该工厂所获利润最大的线性规划。

产品Ⅰ 产品Ⅱ 限额 台时 2 1 40 原材料1330解：设生产产品Ⅰ的数量是1x ，生产产品Ⅱ的数量是2x ，利润是y ，则有2143max x x y +=2143min x x y --=⎪⎩⎪⎨⎧≥≤+≤+;0,;303;402212121x x x x x x⎪⎩⎪⎨⎧≥=++=++;0,,;303;4024,321421321x x x x x x x x x x程序如下：D=[2 1 1 0 40;1 3 0 1 30;-3 -4 0 0 0]; N=[3 4 ];% 求解标准型线性规划:min c*x; s.t. A*x=b; x>=0% 本函数中的D 是单纯初始表，包括:最后一行是判别系数，最后一列是右端向量b ，D 的最后一个元素用0补齐，其余的元素是约束矩阵A % N 是初始的基变量的下标 % 输出变量x 是最优解% 输出变量y 是最优目标值，k 是迭代次数 [mD,nD]=size(D); B=D;k=0;%迭代次数 flag=1; while flag k=k+1;if D(mD,:)>=0 %全体判别系数为非负则已经得到了最优解， flag=0;化为标准型x=zeros(1,nD); %令非基变量xj=0,得到一个基解x,则此时x就是最优解优解for i=1:mD-1x(N(i))=D(i,nD);endy=x*(B(mD,:))'; %x为最优解，B(mD,:)为价格向量，得到y为最优解优解disp('最优值为：')ydisp('最优解为：')xdisp('迭代次数为：')kelsefor i=1:nDif D(mD,i)<0&D(1:mD-1,i)<=0 %若存在判别系数D(mD,i)<0且对所有D(1:mD,i)<=0，则线性规划无最优解disp('无最优解');flag=0;break;endend%存在最优解的情况if flagtemp=0;for i=1:nD-1 %找出最小的判别系数，其下标对应的向量作为进基变量if D(mD,i)<temptemp=D(mD,i);in=i; %进基变量的下标endendsita=zeros(1,mD-1); %确定离基变量for i=1:mD-1if D(i,in)>0sita(i)=D(i,nD)/D(i,in);endendtemp=inf;for i=1:mD-1if sita(i)>0&sita(i)<temptemp=sita(i);out=i; %最小的sita值其下标所对应的向量为离基变量endend%更新初始的基变量的下标向量Nfor i=1:mD-1if i==outN(i)=in;endendD(out,:)=D(out,:)/D(out,in); %主元归一化for i=1:mDif i~=outD(i,:)=D(i,:)-D(i,in)*D(out,:); %将主元所在其它行元素变为零 D(mD,nD)=0;endendendendend程序运行之后的结果是最优值为：y =-70最优解为：x = 18 4 0 0 0迭代次数为：k = 3该工厂所获最大的利润是70，生产产品Ⅰ的数量是18，生产产品Ⅱ的数量是4。

单纯形法与对偶定理单纯形法⼀般oi 中遇到的线性规划问题都长这样⽐如某⼀些⽹络流问题，以及⼆分图最⼤权匹配啥的，结合对偶定理，可以有很多很强的结论以及⼀个最⼩费⽤流的线性规划式⼦现在考虑怎么做这类问题不妨先引⼊⼀个基变量（松弛变量）⽐如说现在的系数矩阵是⽐如说现在的系数矩阵是x 11x 12x 13x 14...x 1n +1x 21x 22x 23x 24...x 2n +1x 31x 32x 33x 34...x 3n +1x 41x 42x 43x 44...x 4n +1...x m 1x m 2x m 3x m 4...x mn +1对于第i ⾏x i ,n +1=b i −n∑j =1x i ,j ∗a i ,j 不妨将第x i ,k 表⽰出来x i ,k =x i ,n +1+∑j != k x i ,j ∗a i ,j −b i−a i ,k给你要最⼤化的式⼦带来的价值是这样可以吧x i ,n +1的值给去x i ,k ,这样的操作叫做转轴之后就可以⽤这个过程来时⽬标函数有最⼤值有⼀个例题吧很容易列出线性规划式⼦max :c 1∗x 1+c 2∗x 2+...+c n ∗x n a 11∗x 1+a 12∗x 2+...+a 1n ∗x n <=b 1..a m 1∗x 1+a m 2∗x 2+...+a mn ∗x n <=b m就是⼀个板⼦题#include<bits/stdc++.h>#define MAXN 500#define eps 1e-7typedef double ll;const ll inf = 1e18;using namespace std;int n,m;ll a[MAXN][MAXN];int id[MAXN];void out(){for(int i = 1 ; i <= n ; i++)printf("%.2f " , a[0][i]); puts("");for(int i = 1 ; i <= m ; i++){ for(int j = 1 ; j <= n ; j++){ printf("%.2f " , a[i][j]); }printf("%.2f " , a[i][0]); puts(""); }}void plot(int x , int y){ swap(id[x + n] , id[y]);double t = a[x][y]; a[x][y] = 1;for(int j = 0 ; j <= n ; j++)a[x][j] /= t; for(int i = 0 ; i <= m ; i++){if(i == x || a[i][y] < eps)continue; t = a[i][y] , a[i][y] = 0;for(int j = 0 ; j <= n ; j++)a[i][j] -= a[x][j] * t; }}bool simplex(){for(int i = 1 ; i <= n ; i++)id[i] = i; int x = 0, y = 0; int cnt = 0; ll minl; while(1){x = y = 0 , minl = inf; cnt++;for(int i = 1 ; i <= n ; i++)if(a[0][i] > eps){x = i;break;} if(!x)break;for(int i = 1 ; i <= m ; i++)if(a[i][x] > eps && minl > a[i][0] / a[i][x])minl = a[i][0] / a[i][x] , y = i; if(!y) {puts("Unbounded"); return false;} plot(y , x); }return true;}int main(){while(scanf("%d%d",&n,&m) == 2){ memset(a , 0 ,sizeof(a));for(int i = 1 ; i <= n ; i++)cin>>a[0][i]; for(int i = 1 ; i <= m ; i++){for(int j = 1 ; j <= n ; j++)cin>>a[i][j]; cin>>a[i][0]; }simplex();printf("Nasa can spend %d taka.\n",(int)ceil(-a[0][0]*m)); }}对偶定理考虑⼀个基本的线性规划模型{}{max :c 1∗x 1+c 2∗x 2+...+c n ∗x n a 11∗x 1+a 12∗x 2+...+a 1n ∗x n <=b 1..a m 1∗x 1+a m 2∗x 2+...+a mn ∗x n <=b mx i >=0其系数矩阵为a 11a 12...a 1n a 21a 22...a 2n a 31a 32...a 3n..a m 1a m 2...a mn那么上⾯这个线性规划模型的对偶问题的系数矩阵为上述系数矩阵的转置矩阵a 11a 12...a 1n a 21a 22...a 2n a 31a 32...a 3n..a m 1a m 2...a mnT 即:a 11a 21...a m 1a 12a 22...a m 2a 13a 32...a m 3..a 1n a 2n ...a nm那么线性规划模型对偶过来就是max :b 1∗y 1+b 2∗y 2+...+b m ∗y m a 11∗x 1+a 21∗x 2+...+a m 1∗x n <=c 1..a 1n ∗y 1+a 2n ∗y 2+...+a nm ∗y m <=c my i >=0基本上⼤多数的线性规划模型都可以通过对x i 的转换化成标准形式不过还是应该列个表:并且注意：原问题有⽆界解等价于对偶问题⽆可⾏解但是对偶问题⽆可⾏解时，原问题可能为⽆界解或者⽆可⾏解线性规划在⽹络流中的应⽤全⼳模矩阵（任何⼀个⾏数列数相同的⼦矩阵的值都是+1/-1）有⼀个很好的性质，对于⼀个线性规划模型的系数矩阵是⼀个全⼳模矩阵，那么有每⼀个单纯形法的调整系数都应当为(-1,0,1)线性规划对偶性--->>可以通过很显然的式⼦推导推导出---->>（最⼤流 = 最⼩割）部分题⽬没有很显然的建图，⼀般是转线性规划，然后看⼀看是不是⼀个全⼳模矩阵，如果是，就可以使⽤⽹络流解决有⼀个可以判断是否是全⼳模矩阵的⽅法直接考虑差分，对于每⼀个约束 + 表⽰⼊，-表⽰出，直接建图，跑⼀个最⼩最⼩费⽤流就好了也可以直接对偶掉，做⼀个单纯形法线性规划与特殊的整数规划前40分可以直接dp 掉还有⼀道题Codeforces 375E,有O (n 3)的dp 做法，但是线性规划可以很快的做掉。

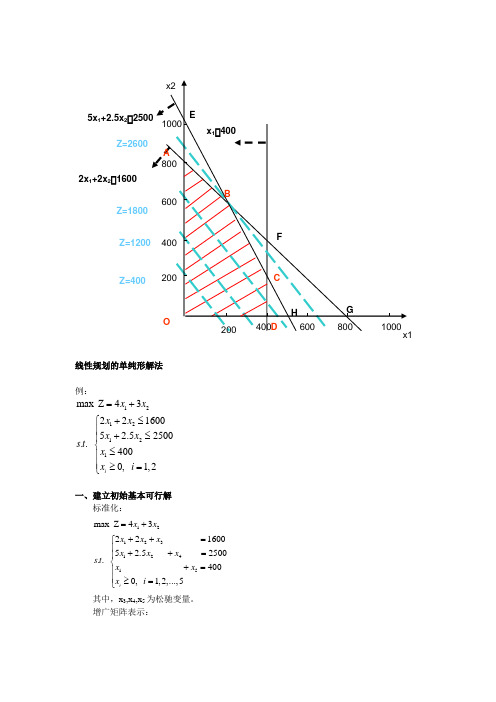
线性规划的单纯形解法 例：1212121max Z 432216005 2.52500.. 4000, 1,2i x x x x x x s t x x i =++≤⎧⎪+≤⎪⎨≤⎪⎪≥=⎩一、建立初始基本可行解标准化：1212312415max Z 4322 16005 2.5 2500.. 4000, 1,2,...,5i x x x x x x x x s t x x x i =+++=⎧⎪++=⎪⎨+=⎪⎪≥=⎩ 其中，x 3,x 4,x 5为松驰变量。

增广矩阵表示：2x 1+2x 2 1600Z=4005x 1+2.5x 212345 2 2 1 0 0 16005 2.5 0 1 0 2500 1 0 0 0 1 400x x x x x b ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦初始可行基：1 1 0 00 1 00 0 1B ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦基变量可用非基变量表示成：3124125116002-225005 2.5400x x x x x x x x=-⎧⎪=--⎨⎪=-⎩ 令非基变量x 1=x 2=0，得初始可行解：X=[0,0,1600,2500,400]，对应于可行域的O 点。

相应的Z 值为0二、解的最优性检验规划判断的方法是检查目标函数中是否还有正的系数。

Z=4x 1+3x 2+0 因此，如果将这两个非基变量中的任意一个变成基变量，也就是使该变量的取值由零变为正值，都有可能使目标函数值增加，因此原来的解不是最优解。

三、第一次迭代（基变换） 1.确定换入变量一般选取价值系数大的那个为入基变量。

这里选择x 1为入基变量。

2.确定换出变量确定入基变量，同时要确定换出变量，其原则是使得到的新的基本解同时是可行解。

分析如下：令x 2=0（x 2仍为非基变量），得：3141511600225005400x x x x x x=-⎧⎪=-⎨⎪=-⎩ 随着x 1的增加，x 3, x 4, x 5的值就会逐渐变小，但始终应保持非负。