第一章河海大学结构力学

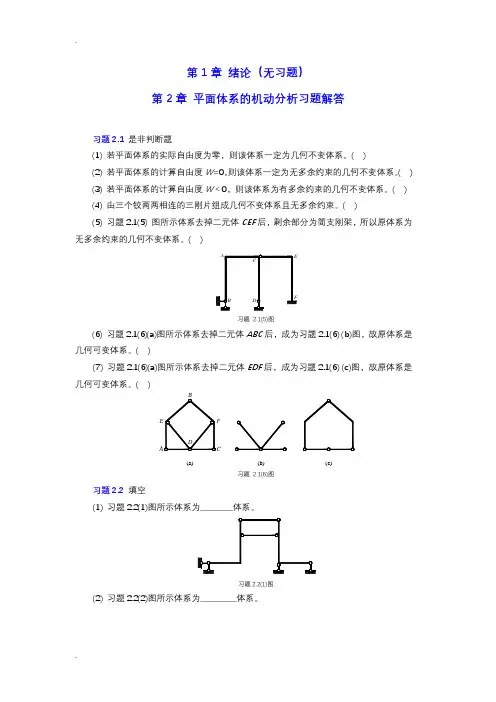
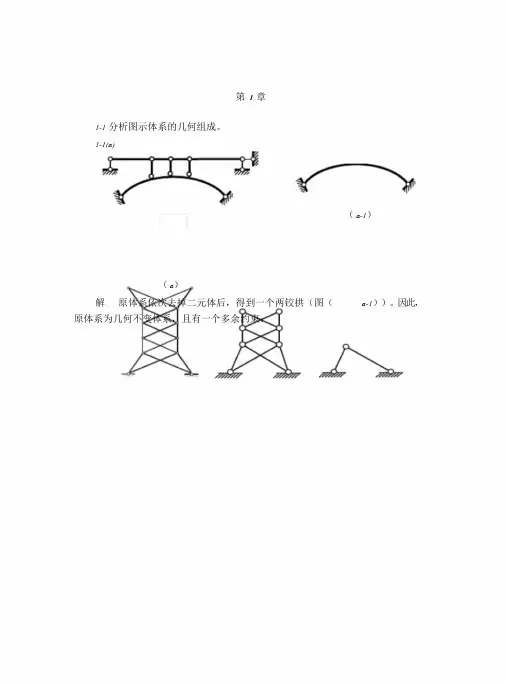
第1章1-1 分析图示体系的几何组成。

1-1(a)（a-1）（a）解原体系依次去掉二元体后，得到一个两铰拱（图（a-1））。

因此，原体系为几何不变体系，且有一个多余约束。

1-1 (b)（b）（b-1）（b-2）解原体系依次去掉二元体后，得到一个三角形。

因此，原体系为几何不变体系，且无多余约束。

1-1 (c)（c）（c-1）（c-2）（c-3）解原体系依次去掉二元体后，得到一个三角形。

因此，原体系为几何不变体系，且无多余约束。

1-1 (d)（d）（d-1）（d-2）（d-3）解原体系依次去掉二元体后，得到一个悬臂杆，如图（d-1）-（d-3）所示。

因此，原体系为几何不变体系，且无多余约束。

注意：这个题的二元体中有的是变了形的，分析要注意确认。

1-1 (e)AABB C（e）（e-1）（e-2）解原体系去掉最右边一个二元体后，得到（e-1）所示体系。

在该体系中，阴影所示的刚片与支链杆 C 组成了一个以 C 为顶点的二元体，也可以去掉，得到（e-2）所示体系。

在图（e-2）中阴影所示的刚片与地基只用两个链杆连接，很明显，这是一个几何可变体系，缺少一个必要约束。

因此，原体系为几何可变体系，缺少一个必要约束。

1-1 (f)（f-1）（f ）解原体系中阴影所示的刚片与体系的其它部分用一个链杆和一个定向支座相连，符合几何不变体系的组成规律。

因此，可以将该刚片和相应的约束去掉只分析其余部分。

很明显，余下的部分（图（f-1））是一个几何不变体系，且无多余约束。

因此，原体系为几何不变体系，且无多余约束。

1-1 (g)（g）（g-1）（g-2）解原体系中阴影所示的刚片与体系的其它部分用三个链杆相连，符合几何不变体系的组成规律。

因此，可以将该刚片和相应的约束去掉，只分析其余部分。

余下的部分（图（g-1））在去掉一个二元体后，只剩下一个悬臂杆（图（g-2））。

因此，原体系为几何不变体系，且无多余约束。

1-1 (h)（h）（h-1）解原体系与基础用一个铰和一个支链杆相连，符合几何不变体系的组成规律。

2013河海大学结构力学(I)基础知识点框架梳理及其解析第一章体系的几何组成分析本章需要重点掌握几何不变体系、自由度、刚片、约束等基本概念，重点掌握几何不变体系组成的三规则——两刚片规则，三刚片规则和二元体规则。

一、基本概念１、几何不变体系：在荷载作用下能保持其几何形状和位置都不改变的体系。

２、几何可变体系：在荷载作用下不能保持其几何形状和位置都不改变的体系。

３、刚片：假想的一个在平面内完全不变形的刚性物体叫作刚片。

在平面杆件体系中，一根直杆、折杆或曲杆都可以视为刚片，并且由这些构件组成的几何不变体系也可视为刚片。

刚片中任一两点间的距离保持不变，既由刚片中任意两点间的一条直线的位置可确定刚片中任一点的位置。

所以可由刚片中的一条直线代表刚片。

４、自由度的概念：一个点：在平面内运动完全不受限制的一个点有２个自由度。

一个刚片：在平面内运动完全不受限制的一个刚片有３个自由度。

５、约束，是能减少体系自由度数的装置。

1）链杆——一根单链杆或一个可动铰（一根支座链杆）具有１个约束。

2）单铰——一个单铰或一个固定铰支座（两个支座链杆）具有两个约束。

3）单刚结点——一个单刚结点或一个固定支座具有３个约束。

6、必要约束：除去该约束后，体系的自由度将增加，这类约束称为必要约束。

多余约束：除去该约束后，体系的自由度不变，这类约束称为多余约束。

7、无多余约束的几何不变体系是静定结构，有多余约束的几何不变体系是超静定结构。

一、几何不变体系的简单组成规则规则一两个刚片之间的连接（两刚片规则）：（图2-3-1）两个刚片用不全交于一点也不全平行的三根链杆相连，组成无多余约束的几何不变体系。

规则二三个刚片之间的接（三刚片规则）：三个刚片用不全在一条直线上的三个单铰（可以是虚铰）两两相连，组成无多余约束的几何不变体系。

规则三刚片与点之间的连接（二元体规则）：二元体特性：在体系上加上或拆去一个二元体，不改变体系原有的自由度数。

利用二元体规则简化体系，使体系的几何组成分析简单明了。

12 31 2 3I 12 31 2 3 第一章 结构的几何构造分析一、基本概念1、几何不变体系、几何可变体系、常变体系、瞬变体系的概念及其相互关系几何不变体系——在不考虑材料应变的条件下，几何形状和位置保持不变的体系。

几何不变体系可以分为无多余约束的几何不变体系（静定结构）和有多余约束的几何不变体系（超静定结构）。

几何可变体系——在不考虑材料应变的条件下，几何形状和位置可以改变的体系，包括常变体系和瞬变体系。

常变体系——如果一个几何可变体系可以发生大位移，则称为几何常变体系。

几何常变体系绝大多数情况下都缺少必要约束，但少数情况下即使不缺少必要约束也可以组成几何常变体系，如图 1-1a 、c 中，刚片 I 、II 之间均由三根链杆相连，不缺少必要约束，但图 a 中三链杆平行等长，图 c 中三链杆交于一实铰，这两种体系都能发生很大的位移，是几何常变体系，发生位移后的情形见图 1-1b 、d 。

瞬变体系——本来是几何可变，经微小位移后又成为几何不变的体系，称为瞬变体系。

其特点是： （1）不缺少必要的约束，但约束的布置不合理，当发生微小位移后，约束的布置变得合理，就成为几何不变体系；（2）在发生微小位移之前，体系具有自由度，因此瞬变体系至少有一个多余约束。

如图 1-2 a 、c 中，均不缺少必要约束，发生微小位移后，三链杆不再交于一点，故原体系为瞬变体系。

相互关系：♣ ♣无多余约束♠几何不变体系（可以作为结构）♦ ♠ 体系♦ ♥有多余约束 ♣常变体系 ♠ 几何可变体系（不能作为结构）♦ ♠♥ (a) I (b)(c) I ♥瞬变体系 (d) IIIII IIII图 1-1(a)(b) (c) I(d)I II2、瞬铰（或虚铰） 2.1 瞬铰的概念IIIIII图 1-2用两根链杆连接两个刚片时，这两根链杆的约束作用相当于一个单铰，该铰的位置在两杆的交点， 我们称这种铰为瞬铰（或虚铰）。

两根平行链杆所起的约束作用相当于无穷远处的瞬铰。

《结构力学》教学大纲一、课程编号 042242课程名称：结构力学Structural mechanics二、教学对象土木工程、水利水电工程、农业水利工程、设施农业科学与工程专业本科生三、先修课程要求高等数学、理论力学和材料力学。

四、本课程的性质和任务本课程是水利类、土建类专业的一门主要技术基础课。

其任务是使学生在学习理论力学和材料力学等课程的基础上进一步掌握杆系结构的计算原理和方法，了解各类结构受力性能，为学习有关专业课程以及进行结构设计和科学研究打下良好的力学基础。

培养学生结构分析与计算等方面的能力。

五、本课程的教学内容（一）绪论结构力学的研究对象及任务。

荷载的分类、结构的计算简图及其分类。

平面体系的几何组成分析。

静定结构的内力计算与特性回顾（二）虚功原理和结构的位移计算外力虚功，虚变形功，虚功原理。

虚位移原理与单位位移法。

虚力原理与单位荷载法。

结构位移计算的一般公式。

荷载作用下结构的位移计算及图乘法。

温度变化及支座移动引起的结构位移计算。

互等定理。

（三）力法静定结构的概念。

超静定次数的确定。

力法的基本原理。

基本系与基本未知量，力法的典型方程及其物理意义。

用力法计算简单超静定刚架、超静定桁架和超静定组合结构。

对称性利用。

超静定拱的计算。

温度变化及支座移动下超静定结构的计算。

超静定结构的位移计算，最后内力图的校核。

超静定结构的特性。

等截面直杆的转角位移方程（四）位移法位移法的基本原理。

基本系与基本未知量，位移法的典型方程及其物理意义。

荷载作用下超静定刚架的计算。

对称性利用。

*支座移动下的计算。

力矩分配法的概念及其应用。

近似法。

（五）影响线移动荷载的概念，影响线的概念。

用静力法作静定梁的影响线。

结点荷载作用下的影响线。

用机动法作静定梁的影响线。

桁架的影响线。

*连续梁影响线的概念影响量的计算。

最不利荷载位置的确定。

内力包络图。

*简支梁的绝对最大弯矩。

（六） *超静定结构补充讨论超静定结构计算方法的讨论。