当前位置：文档之家 › 第九章 矩阵位移法-河海大学

第九章 矩阵位移法-河海大学

  • 格式：ppt
  • 大小：2.04 MB
  • 文档页数：78

下载文档原格式

  / 78

合集下载

《结构力学》第9章矩阵位移法.

《结构力学》第9章矩阵位移法.
3.结点位移整体编码
对结构整体建立坐标系oxyz，则每个结点都有确定的位置坐标。
下标I表示结点编号，上标T表示矩阵转置。
结构力学
对结构所有的结点位移，统一用矢量Δ表示，称为结构整体位 移，简称结构位移或整体位移。Δ中各分量的顺序首先是结点 编号，然后是每个点本身的x,y,z顺序，即
对应结点载荷用矢量F表示，它的排序与位移排序相同
整体坐标系下单元杆端力与杆端位移间的关系—刚度方程： 简写为 其中Ke称为整体坐标系下的单元刚度矩阵。
结构力学
9.4 结构的整体刚度方程和整体刚度矩阵
上式称为结构的整体刚度方程，其中K称为结构的整体刚度 矩阵。
总体刚度矩阵是一个方阵，其阶数与结构结点位移分量总 数相同。它的分量是由单元刚度矩阵的系数叠加构成的。叠加 规律是：单元刚度矩阵的元素，按照它所处的局部行和列号， 对应单元的定位向量，在总刚度矩阵中落到新的行和列上。 总刚度矩阵的特点： (1)刚度矩阵的系数是物理量，由结构本身的长度、截面尺寸、 材料性质、连接方式等决定，与载荷、变形等量无关。 (2)总刚度系数kij表示结构沿第j个整体结点位移方向产生单位 位移Δj=1，其他所有结点位移等于0时，在第i结点位移方向所 需要施加的力(与传统位移法相同)。
结构力学
9.5 非结点荷载的等效化
计算步骤： 1. 在局部坐标系下计算单元的等效载荷 2. 将固端力转换到结构(整体)坐标系 3. 等效结点载荷FP
结构力学
9.6 计算步骤和算例
矩阵位移法的基本步骤如下：
(1)整理原始数据，对结点位移进行整体编码，得到单元定位向量等。 直接的结点载荷按它对应的结点位移编码，直接计入整体结点载荷向量 F中。 (2)单元分析，先形成局部坐标系中的单元刚度矩阵 ，用式(9-10)。 再形成整体坐标系中的单元刚度矩阵Ke，用式(9-24)。 (3)整体分析，依定位向量，将单元刚度矩阵“对号入座”集成总刚度 矩阵K。

09矩阵位移法(学习版)(1)

09矩阵位移法(学习版)(1)

1
2
3 6
4
y
5
θ x
O
练习：
3 ④ 2 ① 1
8 ⑨ ⑤ 6 ⑦ ② 4 5 ⑧ 7 ⑩ ⑥
13
12 10 11 ③ 9
（2）结点位移编码 矩阵位移法基本未知量的确定： 矩阵位移法基本未知量的确定不是唯一的，它与 单元如何划分，是否考虑轴向变形以及如何编写程序 有关。 结点位移的统一编码 —— 整体码 用矩阵位移法进行结构分析时，基本未知量是结点 位移，这就需要将结构中全部结点位移分量进行统一编 码。
第九章
矩阵位移法
9.1 概述
1. 概述
结构矩阵分析是采用矩阵方法分析结构力学问题的 一种方法。与传统的力法、位移法相对应，结构矩阵分 析中也有矩阵力法和矩阵位移法，或柔度法与刚度法。 矩阵位移法易于实现计算过程程序化而被广泛应用。 矩阵位移法是以结点位移为基本未知量，借助矩阵 进行分析，并用计算机解决各种杆系结构受力、变形等 计算的方法。
e
e
建立单元的杆端力和杆端 位移之间关系的过程称单元分 析，形成的方程称单元刚度方 程。
e
⎡δ 1 ⎤ ⎡ u i ⎤ ⎢ ⎥ ⎢ ⎥ δ 2 ⎥ ⎢ vi ⎥ ⎢ e ⎡ δ i ⎤ ⎢δ 3 ⎥ ⎢θ i ⎥ e δ =⎢ ⎥ =⎢ ⎥ =⎢ ⎥ ⎣δ j ⎦ ⎢δ 4 ⎥ ⎢u j ⎥ ⎢δ 5 ⎥ ⎢ v j ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎦ ⎦ ⎢ ⎣θ j ⎥ ⎣δ 6 ⎥
2. 单元分析
y y e i x
α
j x
局部坐标系（单元坐标系）：进行某一单元的单元分析时所 建立的坐标系。 局部坐标系相对于整体坐标系的方位角用α表示。α的方向 以 x 轴向 x 轴逆时针转动为正。即便在一个结构中，各单元的局 部坐标系也不完全相同。

矩阵位移法

矩阵位移法

第9章矩阵位移法本章介绍矩阵位移法的原理、概念和方法,并随时给出常用的计算机编码方法，最后给出了平面刚架的计算程序。

9.1 概述结构在载荷作用下产生的内力和变形，可以用力法、位移法或混合法进行分析。

其基本原理在材料力学中已经给出，在结构力学中得到广泛运用。

通常将分析过程中得到的公式联立成为方程组。

可以用代数方法求解这个方程组；也可以将方程组用矩阵形式表示，通过矩阵运算进行求解。

后者被称为矩阵方法。

矩阵方法表现形式简洁紧凑，能够突出和利用方程组的某些特点,可以用计算机程序求解。

用矩阵方法分析结构力学问题就称为结构矩阵分析法(结构矩阵分析原理)。

结构矩阵分析法包括力学和数学两个方面：用力法、位移法或混合法(力学知识)建立方程组，用矩阵方法(数学知识)表示和求解方程组。

与建立方程组时所用的力法、位移法或混合法相对应，结构矩阵分析法也分为矩阵力法、矩阵位移法或矩阵混合法。

混合法在杆件结构分析中很少采用；力法求解过程灵活多变，比较难于编制通用的计算机程序；位移法思路清晰，具有统一的模式，特别适合于用计算机程序实现，因而，矩阵位移法得到广泛的应用。

考虑到计算工作量,用位移法手工分析实际的工程结构，只具有理论上的意义而并不具有太多的现实意义。

矩阵位移法是为了用计算机进行结构分析而发展起来的。

可以从梳理以前的手工分析方法(位移法)入手，找出其中的规律，结合用计算机进行计算的特点，提出一些概念，形成一套适合的计算流程，提出相应的编码方法，编制计算机程序。

在本章学习过程中，要特别注意以前熟悉的方法和过程是怎样用编码表达的，从而培养自己的编码能力。

最好能够熟悉一门计算机算法语言，例如BASIC、C/C++或FORTRAN。

目前，在微型计算机上的开发环境中，推荐使用Microsoft Visual Basic 2005、Microsoft Visual C++ 2005和Intel® Visual Fortran Compiler 9.1。

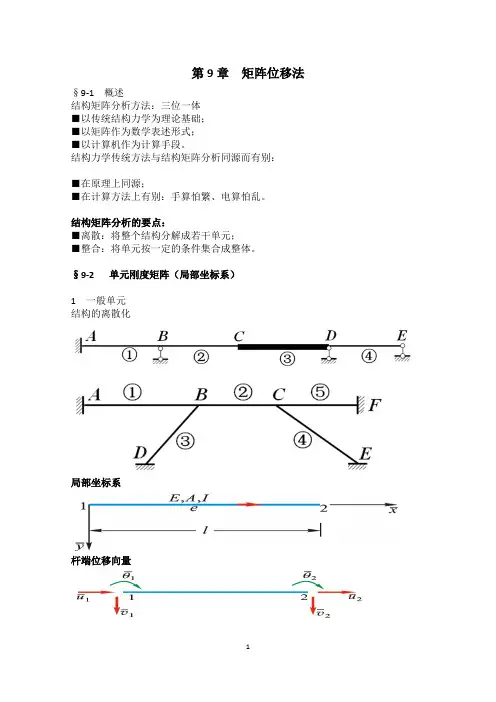
结构力学教学课件-09矩阵位移法

结构力学教学课件-09矩阵位移法
实践应用
学习者可以通过实际的结构分析案例，将矩阵位移法应用于实际问题中，加深理解和掌 握。
THANKS
感谢观看
矢量与张量
在结构力学中，矢量与张量是描述结 构内力和位移的重要工具，矩阵位移 法中需要用到这些概念。
矩阵位移法的计算步骤
建立结构离散化模型
将结构划分为若干个离散的单元，每个单元 具有一定的自由度。
建立单元刚度方程
根据结构力学中的刚度原理，建立每个单元 的刚度方程。
集成整体刚度方程
将所有单元的刚度方程集成在一起，形成整 体刚度方程。
课程目标
掌握矩阵位移法的基本原理和步骤，理解如何应 用矩阵位移法解决实际工程问题。
学会使用相关软件进行结构分析，提高解决实际 问题的能力。
培养学生对结构力学学科的兴趣和热爱，为今后 从事土木工程领域的工作打下基础。
02
矩阵位移法基础
矩阵位移法概述
矩阵位移法是一种基于矩阵运算的数值分析方法，用 于解决结构力学中的位移问题。
结构力学教学课件-09矩阵位移法
目 录
• 引言 • 矩阵位移法基础 • 矩阵位移法的基本原理 • 矩阵位移法的应用实例 • 结论
01
引言
课程背景
01
结构力学是土木工程学科中的重 要基础课程，矩阵位移法是结构 力学中的一种重要分析方法，用 于解决结构的位移和内力问题。
02
随着计算机技术的发展，矩阵位 移法在结构分析中得到了广泛应 用，因此掌握矩阵位移法对于土 木工程师来说具有重要意义。
矩阵位移法的应用范围
矩阵位移法广泛应用于各种工程结构的分析，如桥梁、建筑、机械等 。
下一步学习建议
深入学习矩阵位移法的数学基础
为了更好地理解和应用矩阵位移法，建议学习者深入学习线性代数和数值分析等相关数 学基础。

矩阵位移法

矩阵位移法

第9章矩阵位移法§9-1 概述结构矩阵分析方法：三位一体■以传统结构力学为理论基础；■以矩阵作为数学表述形式；■以计算机作为计算手段。

结构力学传统方法与结构矩阵分析同源而有别：■在原理上同源；■在计算方法上有别：手算怕繁、电算怕乱。

结构矩阵分析的要点：■离散：将整个结构分解成若干单元；■整合：将单元按一定的条件集合成整体。

§9-2 单元刚度矩阵（局部坐标系）1 一般单元结构的离散化局部坐标系杆端位移向量()()()()()()()()T123456T111222e e e u v u v θθ=∆∆∆∆∆∆=Δ杆端力向量■弯矩、转角：绕杆端顺时针为正； ■其它：与坐标轴同向为正。

单元刚度方程由单元杆端位移求单元杆端力时所建立的方程。

首先 在杆端两端加上人为控制的附加约束，使体系发生任意指定的位移。

然后 根据位移推算相应的杆端力。

忽略轴向受力状态和弯曲受力状态之间的相互影响，得 ()()()()()()()()T 123456T111222e ee x y x y F F F F F F F F F M F F M ==11211122323211122222121261266462126126x y x EA EA F u ul l EI EI EI EIF v v l l l l EI EI EI EIM v v l l l l EA EAF u u l lEI EI EI EIF v v θθθθθθ=-=+-+=+-+=-+=--+-局部坐标下的单元刚度方程局部坐标下自由单元的单元刚度矩阵 2 单元刚度矩阵的性质（1）单元刚度系数的意义 单位杆端位移引起的杆端力 （2）单元刚度矩阵是对称矩阵 反力互等定理 （3）自由单元刚度矩阵是奇异矩阵 矩阵行列式等于零，逆阵不存在。

解唯一,解不唯一由杆端力只能求出变形，不能求杆端总的位移（刚体位移+变形）。

3 特殊单元连续梁单元的刚度方程单元刚度方程为 单元刚度矩阵为非奇异，可逆§9-3 单元刚度矩阵（整体坐标系）（1）单元坐标转换矩阵局部坐标系下的杆端力整体坐标系下的杆端力同理： （2）整体坐标系下的单元刚度矩阵1T T T -=整体坐标下的单元刚度方程整体坐标下的单元刚度矩阵性质1）整体坐标系下单元杆端位移引起的杆端力；（2）对称矩阵；（3）奇异矩阵。

第9章矩阵位移法

第9章矩阵位移法

方程后求出原结构的结点位移和内力，称该过程为整体分析。 上述一分一合，先拆后搭的过程中，是将复杂结构的计算
问题转化为简单单元的分析及集合问题。而由单元刚度矩阵直 接形成结构刚度矩阵是矩阵位移法的核心内容。
水 利 土 木 工 程 学 院 结 构 力 学 课 程 组
第9章 矩 阵 位 移 法
§9.1 概 述
第9章
矩 阵 位 移 法
§ 9.1 概
述
§9.2 局部坐标系下的单元刚度矩阵
§9.3 整体坐标系下的单元刚度矩阵 §9.4 用矩阵位移法解连续梁 §9.5 用矩阵位移法解平面刚架 §9.6 用矩阵位移法解平面桁架和组合结构
第9章 矩 阵 位 移 法
§9.1 概 述
二、矩阵位移法基本思路
2、用矩阵形式解该题 位移法方程：
4i11+2i12=M1 2i11+(4i1+4i2)2+2i23 =M2 2i22+4i23= M3
1
M1
i1
1
M2
i2
②
3
M3
①
单元① 刚度矩阵
2
2
3
整体 刚度矩阵
1 M 1 2 M 2 3 M 3
3、矩阵位移法 ——杆件结构的有限单元法 它是以结点位移作为基本未知量的结构分析方法。由于 它易于实现计算过程程序化，本章只对矩阵位移法进行讨论。
水 利 土 木 工 程 学 院 结 构 力 学 课 程 组
第9章 矩 阵 位 移 法
§9.1 概 述
二、矩阵位移法基本思路
1、用位移法解该题 未知量：1、2、3
如图所示，xOy为整体坐标系， 按右手定则确定，1、2、3、4称 为整体码。 y x o y为局部坐标系，按右手 定则确定， 1 、 2 称为局部码。 通常原点O放在结点 1上， x 轴与 单元轴线重合，正方向由 1 指向 2 。

矩阵位移法-资料

矩阵位移法-资料

即用轴力、剪力、弯矩和水平位移分量u、竖直位
移分量v、转角位移分量q 等我们熟知的表示方法
来绘制。采取传统方法表示时，各分量用下标注明 其作用的结点；同时，若参照系为单元坐标系，各 分量还需添加上划线以示区别。
公式（9.1）和（9.2）给出了参照系为单元坐 标系时，分别使用广义方式和传统方式表示的单元 杆端力和杆端位移列阵。
i
f 2 ( 2)
y
e
j f 5 ( 5)
x f 6 ( 6)
f 4 ( 4)
(c) 整体坐标系下的广义分量
Mi( i) O
Fxi ( ui )
i
Fyi ( vi )
y
x
e Mj( j)
j Fyj ( vj )
Fxj ( uj )
(d) 整体坐标系下的分量
14
土木工程专业系列教材—结构力学
出版出社版科社技分科社技分社
f 3 ( 3)
f1 ( 1)
i
e
f 2 ( 2)
j f 6 ( 6)
y
f 5 ( 5)
x
f4 ( 4)
(a) 单元坐标系下的广义分量
Mi ( i)
FNi
(
u i
)
i
e
FQi ( vi )
j Mj ( j )
y
FQj ( vj )
FNj
(
u j
)
x
(b) 单元坐标系下的分量
f 3 ( 3) O
f 1 ( 1)
上图中（a）和（c）标明了两套坐标系中所有 24个广义分量（括号中的是广义位移分量）。约定 各分量与相应坐标系正向一致时为正，力矩或转角 分量以顺时针转动为正，反之为负。

《矩阵位移法》课件

《矩阵位移法》课件

实际工程案例分析
总结词
为了验证矩阵位移法的有效性，可以通过实际工程案例 进行分析。通过与实验结果的对比，可以评估方法的精 度和可靠性。
详细描述
选取具有代表性的实际工程案例，如高层建筑、大跨度 桥梁等，利用矩阵位移法进行计算，并将结果与实验数 据进行对比。通过对比分析，可以评估矩阵位移法的精 度和可靠性，为该方法在实际工程中的应用提供依据。 同时，也可以针对不同工程案例的特点，对矩阵位移法 进行优化和改进，提高其适用性和计算效率。
05
矩阵位移法的优缺点
优点
精确度高
矩阵位移法基于严格的数学推导，能 够精确地计算出结构的位移和内力， 尤其适用于复杂结构的分析。
适用性强
矩阵位移法可以处理多种类型的载荷 ，包括静载、动载以及温度载荷等， 适用范围广泛。
便于计算机化
矩阵位移法的计算过程可以通过计算 机程序实现，便于进行大规模的结构 分析。
多尺度方法
将矩阵位移法应用于多尺度问题 ，考虑不同尺度之间的相互作用 和影响，为复杂系统提供更准确 的模拟结果。
THANKS
感谢观看ts
目录
• 引言 • 矩阵位移法的基本概念 • 矩阵位移法的实施步骤 • 矩阵位移法的应用实例 • 矩阵位移法的优缺点 • 未来展望与研究方向
01
引言
什么是矩阵位移法
矩阵位移法是一种数值分析方法，用 于求解线性方程组和解决各种数值计 算问题。
它通过将原问题转化为矩阵形式，利 用矩阵运算来求解未知数，具有高效 、精确和灵活的特点。
并行计算
利用并行计算技术，将计算任务分解为多个子任务，同时运行在多 个处理器上，加快计算速度。
智能优化
结合人工智能和机器学习技术，自动调整算法参数，实现自适应优 化，提高算法的效率和稳定性。

矩阵位移法

矩阵位移法
(a)
TT T T T T I
Fx1 F y1 M1 单元坐标 转换矩阵 F x2 Fy 2 M 2
e
Hale Waihona Puke eF e TF e
T 1 T T
单元坐标转换矩阵T是一正交矩阵。
EI 25 104 kN m l
0 300 0
5m
0 为了简洁，下面将矩阵 中各元素的单位略去。 12 30 0 12 30 30 100 0 30 50 4 EA 10 0 0 l 0 0 300 0 0 12 30 0 12 30 12 EI 6 EI [k11 ] 0 3 2 30 50 0 30 100 l l 6 EI 4 EI 第一列元素变符号即第四列，第二列元素变符号即第五列 0 ①： 2 ②求整体坐标系中的单刚， k l l 第一行元素变符号即第四行，第二行元素变符号即第五行
3、有限单元法的三个基本环节： ①单元划分：一根等截面直杆作为一个单元，单元间由结点相联。 ②单元分析：建立单元刚度方程，形成单元刚度矩阵(物理关系)。 ③整体分析：由单元刚度矩阵形成整体刚度矩阵，建立结构的 位移法基本方程(几何关系、平衡条件)。
§9-2 单元刚度矩阵(element stiffnessmatrix)（局部坐标系）
T11 T12 T T T 21 22
因此，(a)式的逆转换式为： 同理
F e T TF e
e T e
(b)
e T T e
整体坐标系中的单元刚度矩阵
F e TF e
(a)
e T e
(b)
单元刚度矩阵的性质 设局部坐标系中、整体坐标系中的单元刚度方程分别为： ①单元刚度矩阵是杆端力用杆端位移来表达的联系矩阵。 e e e F k Δ (c) ②其中每个元素称为单元刚度系数，表示由于单位杆端位移引起的杆端力。 ③单元刚度矩阵是对称矩阵。 F e k eΔe (d ) ④第k列元素分别表示当第k个杆端位移=1时引起的六个杆端力分量。 e e e e ⑤一般单元刚度矩阵是奇异矩阵。不存在逆矩阵。因此， 将式(a)、(b)代入式(c) k eT IF T T TTF ke T T 可由单元刚度方程，由杆端位移唯一确定杆端力；但由杆端力反推杆端位移时， 可能无解、可能解不唯一。 k e T T k eT

矩阵位移法

矩阵位移法

D1 = D2 = 0
； D5 = D6 = 0
则有修正后的总刚度矩阵：
-100 2 [K ] = 100 600
[k11 ] [k12 ] {F1} = {F2 } [k 21 ] [k 22 ]
{D1} {D 2 }
@
单元刚度矩阵的性质：①对称性；②奇异性； ③主对角元恒为正值
3、整体刚度矩阵
K ij ：单元仅发生第j个杆端单位位移时，在第
Y2 = QBA
写成矩阵表达式为：
4 EI 2 EI 6 EI q + q + -v ) ( v l 1 l 2 l2 1 2 2 EI 4 EI 6 EI q + q + -v ) ( M2 = v l 1 l 2 l2 1 2 6 EI 12 EI (v1 - v2 ) Y1 = (q1 +q 2 ) + l2 l2 6 EI 12 EI = q + q (v1 - v2 ) Y2 ( 1 2) l2 l2 M1 =
2
3
1 2
Hale Waihona Puke 3-1 50 1 50 50 300 -50 150 -1 -50 2 -100 -1 -50 = 50 150 -100 600 50 150 -1 50 1 50 -50 150 50 300
计入边界条件：因边界结点1和3 为固定端，故有：
0 12EI l3 6 EI - 2 l 0 12EI l3 6 EI - 2 l
@
0 6 EI l2 2 EI l 0 6 EI - 2 l 4 EI l
EA l 0 0

结构力学-矩阵位移法

结构力学-矩阵位移法
Fxe1, Fye1, u1e , v2e , Fxe2 , Fye2 , u2e , v2e
以上杆端力和杆端线位移与相应的坐标轴正 方向一致为正，相反为负。
M1e，M 2e，1e，2e，M1e，M 2e，1e ,2e
以上杆端力矩和杆端转角均以顺时针方向为 正，逆时针方向为负。
10
3. 单元坐标转换矩阵
③
4
④
7
⑤
⑥
1
36
曲杆可用多段直杆近似代替(以直代曲)。
进行结点编号时，要尽量使单元两端结点编号 的差值最小。
4
三、单元杆端力和杆端位移的坐标变换
1．坐标系
结构整体分析 —整体坐标系xy
x
2
②
4
y
①③
④
单元分析—局部坐标系 x y 1
3
单元始端指向末端的方向就
是 x 轴的正方向
1
x
坐标轴遵循右手法则，即
Fx1e
M
e 1
1
M
e 1
e
y
x
2
y
x
单元杆端力
x
2
②
4
y
①③
④
1
3
y v1e 1
1
u1e
u1e
v1e
1e
1e
e
y
x
2
x
2
单元杆端位移
7
Fxe1 Fye1
uv11ee
F
e
MFxe12e
e
u12ee
Fye2
v2e
M
e 2
e 2
Fxe1 Fye1
uv11ee
点，单元与单元、单元与支座均通

矩阵位移法

矩阵位移法
由
e
=0
因此它的逆矩阵不存在
从力学上的理解是，根据单元刚度方程 F
由
F e F e e
e
= k
e
e
e
有一组力的解答(唯一的)，即正问题。 如果 F

e
不是一组平衡力系则无解；若是一
组平衡力系，则解答不是唯一的，即反问题。
正问题
(Δ F)
反问题
0 6 EI l2 4 EI l 0 6 EI - 2 l 2 EI l
EA l 0 0 EA l 0 0
0 12EI - 3 l 6 EI - 2 l 0 12EI l3 6 EI - 2 l
0 6 EI l2 2 EI l 0 6 EI - 2 l 4 EI l

例如 k52 = -
e
12 EI 代表单元杆端第2个位移分量 v1 = 1 时所引起的第5个杆 3 l 端力分量 Y2 的数值。
（2）单元刚度矩阵 k

e
即 kij = k ji。 是对称矩阵，
（3）一般单元的刚度矩阵 k

e
是奇异矩阵；
从数学上可以证明一般单元的刚度矩阵 k

e
的行列式
k
当p = l 时才能相乘
共形
2× 2
2 ×1
非 共形
b11 a11 a12 B A= a a b 21 21 22 2 ×1 2 ×2
（2）不具有交换律，即
AB BA
6、转置矩阵
将一个阶矩阵的行和列依次互换，所得的阶矩阵称之为
原矩阵的转置矩阵，如：
a11 a12 A= a21 a22 a31 a32

结构力学 矩阵位移法

结构力学 矩阵位移法

F1 K111 K122 K133 4i11 2i12
F2 K211 K222 K233 2i11 4i1 4i2 2 2i23
F3 K311 K322 K333 2i22 4i23
写成矩阵形式
l 2EI
l
2EI e
e
l 4EI

1

2
l
4EI
k
e


l 2E
I
l
2EI e
l 4EI

l
§9-2节 单元刚度矩阵(局部坐标系)
⑵桁架结构中杆件单元
e EA

Fx1

Fx2


l EA
l
F x1 e

4i1 2i1
2i1
4i1

F1
F2
①
1
F1①
②
2
F2①
①
②
1
2
F1② 0
+ F2②
①
②
2
F3 3 F3① 0
F3② 3
§9-4节 连续梁的整体刚度矩阵
F1① 4i1 2i1 01
F①

F2①

2i1
4i1
0

2

F3① 0
Fy1
cos sin
sin cos
0 0

M
1


Fx2
0 0
01 00
0 0 0 cos
0 0 0 sin
0 e Fx1 e
0

第九章 矩阵位移法

第九章 矩阵位移法
平衡条件 变形条件
整体分析
结构内力 位移
2、基本概念

结构的离散化，是把结构假想地划分成若干个相互分离的有限个 独立杆件，其中每个独立的杆件称为单元，用字母e表示，单元 与单元之间用结点连接。用这样离散化的单元集合体来代替原结 构，其目的是为了将问题简化，以便于进行单元分析。通常用①， ②，„表示单元编号，用1，2，„表示结点编号。
2、基本概念


整体坐标系，不随单元方向变化而变化，用来描述结 构整体的变形和受力。在一个结构中，整体坐标系只 有唯一的一个，用符号xoy表示。 杆端力。作用在单元两端的力称为杆端力，在平面杆 件结构中，一般情况下，单元每端有三个杆端力分量， 即轴力、剪力、弯矩。单元e的杆端力向量表示如下：
F(2) F(3) F(4) F(5) F(6) }eT { Fx1 Fy1 M1 Fx 2 Fy 2 M 2 }eT
3 2 1
① ③ ②
4
④
5
⑤
6
6 7
5
4
3
2
1
⑥
⑤
④
③
②
①

2、基本概念

局部坐标系，也称为单元坐标系，在杆单元中，局部 坐标系轴与杆轴重合，坐标原点放在单元的某一端1点 （始端）上，从 1 端指向单元另一端2端（终端）的 方向为轴正向，自轴顺时针旋转的方向为轴正向，用 符号表示单元坐标系，其中字母的上面都划上一横线 作为局部坐标系的标志。局部坐标系用来描述单元的 变形和杆端力。每个单元都有各自独立的局部坐标系， 方向一般不同。
（2）对称性：单元刚度矩阵是一个对称矩阵。（反力互 等） （3）奇异性：单元刚度矩阵是一个奇异矩阵。（行列式 为零）
3、特殊单元的刚度矩阵

结构力学教学课件09矩阵位移法ppt

结构力学教学课件09矩阵位移法ppt
所在行、列的副元素以及同行 的未知结点荷载改为0
满足边界条件3 0，
保持矩阵原有阶数和对称性
上节课内容概述
✓边界支承条件的处理； ✓非节点荷载的移置； ✓连续梁的矩阵分析； ✓坐标变换
静力等效原则 移到邻近结点
仅有结点荷载 作用的结构
假想约束 固定各结点
M1F, j
&
M
F 2
,
j
矩阵位移法 分析
0
0.4
69
0.625
0
0.469
1.25
（1） 各杆在局部坐标系中的 单元刚度矩阵
3.0
0
k
(2)
106
0 3.0
0
0
0 0.12 0.3
0 0.12
0.3
0 0.3 1.0 0 0.3 0.5
3.0 0 0 3.0 0 0
0 0.12 0.3
0 0.12 0.3
单元①
1
1
2 2
单元②
1
2
2 3
刚架的整体刚度矩阵,对号入座
k
k11 k21
(1) (1)
k (1) 12
k22 (1) k11 (2) k (2)
21
k12
(2)
k22
(2)
3.75 0
0 3.75 0
0
0
0
0
0
0.234 0.469
0 0.234 0.469
0.6 0.8 0 0
0
0
T
0 0
0
0
01 0
0 0
0 0 cos sin 0
0 0 sin cos 0
00 0

矩阵位移法

矩阵位移法
构分析方法。基于该法的结构分析程序在结构设计中得到 了广泛的应用。因此，以计算机进行结构分析是本章的学 习目的。 矩阵位移法是以位移法为理论基础，以矩阵为表现形 式，以计算机为运算工具的综合分析方法。引入矩阵运算 的目的是使计算过程程序化，便于计算机自动化处理。尽 管矩阵位移法运算模式呆板，过程繁杂，但这些正是计算 机所需要的和十分容易解决的。矩阵位移法的特点是用 “机算”代替“手算”。因此，学习本章是既要了解它与 位移法的共同点，更要了解它的一些新手法和新思想。
e vi
0 12 EI l3 6 EI l2 0 12 EI l3 6 EI l2
i
0 6 EI l2 4 EI l 0
e
u
0 0 EA l 0 0
e j
v
0
e j

0
e j

e FNi
EA l
12 EI l3 6 EI 2 l 0 12 EI l3 6 EI 2 l
单元(自由单元),两端设有任何支承约束,因此,杆件除了由杆端
力所引起的弹性变形外,还可以具有任意的刚体位移。
3. 特殊单元的刚度矩阵 （1）不考虑轴向变形的刚架单元 由于
u u 0
e i e j
，可将式（9—5）中删去与轴向
变形对应的行和列（即第1、4行和1、4列），则
12EI 3 l 6 EI l2 12EI l3 6 EI l2 6 EI l2 4 EI l 6 EI 2 l 2 EI l 12EI l3 6 EI 2 l 12EI l3 6 EI 2 l 6 EI 2 l 4 EI l 6 EI l2 2 EI l

结构力学 矩阵位移法

结构力学 矩阵位移法

§9-2节 单元刚度矩阵(局部坐标系)
一.一般单元的刚度方程和刚度矩阵
1.单元两端采用局部编码1、2
1
e
2.六个杆端位移组成杆端位移列向量。
v1
1
u1
EAI L
3.六个杆端力组成杆端力列向量。
y
2
2 vu22 x
e
1
2
e
u1 v1
e
3
1
F1
e
F2
e
F x1 Fy1
单元刚度矩阵中的每个元素都代表单元
杆端单位位移引起的杆端力称之为单元
刚度系数。其中
k
表示第j个杆端单位位移
ij
引起的第i个杆端力。
⑵单元刚度矩阵为对称矩阵。 kij k ji
⑶一般单元刚度矩阵为奇异矩阵 k e 0
三、特殊单元刚度方程和刚度矩阵
⑴连续梁中的受弯杆件单元 ⑵桁架结构中杆件单元
⑴连续梁中的受弯杆件单元
忽略轴变时单元的刚度矩阵
12EI
l3 6EI
k
e
l2
12E
l3 6EI
I
l2
6EI
l2 4EI
l 6EI
l2 2EI
l
12EI l3
6EI l2
12EI
l3 6EI l2
6EI
e
l2 2EI
l
6EI l2
4EI
l
§9-3节 单元刚度矩阵(整体坐标系)
一、单元坐标转换矩阵
⑶根据所选基本未知量的不同，结构矩阵分析 包括：
§9-1节 位移法概述
矩阵力法
结构矩阵分析
一般刚度法
矩阵位移法
直接刚度法

教案 第九章 矩阵位移法[33页]

教案 第九章 矩阵位移法[33页]

第九章矩阵位移法（4学时）1.主要内容9-1 概述9-2 单元刚度矩阵——局部坐标系9-3 单元刚度矩阵——整体坐标系9-4 用先处理法建立结构刚度矩阵9-5 等效结点荷载2.知识点9-1 概述矩阵位移法的理论基础、数学形式；矩阵位移法与传统位移法的比较：单元分析、整体分析。

9-2 单元刚度矩阵-局部坐标系一般单元、单元刚度方程、单元刚度矩阵的性质、特殊单元。

9-3 单元刚度矩阵-整体坐标系单元坐标转换矩阵；整体坐标系的单元刚度矩阵：元素k ij的物理意义、对称性、奇异性。

9-4 用先处理法建立结构刚度矩阵先处理法的概念与特点、结点位移分量的统一编码、单元单位向量、刚架的整体刚度矩阵、铰结点的处理、忽略轴向变形时刚架整体分析、桁架整体分析。

9-5 等效结点荷载结点荷载与非结点荷载；单元集成法求等效结点荷载。

3.重点难点9-2 单元刚度矩阵-局部坐标系重点：一般单元的单元刚度矩阵。

难点：单元刚度矩阵的性质。

9-3 单元刚度矩阵-整体坐标系重点：整体坐标系的单元刚度矩阵的计算。

难点：整体坐标系的单元刚度矩阵与局部坐标系的单元刚度矩阵的异同。

9-4 用先处理法建立结构刚度矩阵重点：不同情况下整体刚度矩阵的计算。

难点：单元定位向量的确定、特殊情况的处理。

9-5 等效结点荷载重点：单元集成法求整体等效结点荷载的步骤。

难点：等效结点荷载的概念。

9.1 概述知识点：矩阵位移法的理论基础、数学形式；矩阵位移法与传统位移法的比较：单元分析、整体分析。

知识点：矩阵位移法的理论基础、数学形式理论基础：传统的结构力学数学形式：矩阵计算手段：电子计算机知识点：矩阵位移法与传统位移法的比较化整为零——单元分析单元刚度矩阵单元刚度方程集零为整——整体分析形成整体刚度矩阵总体刚度方程9.2 单元刚度矩阵-局部坐标系1. 知识点一般单元、单元刚度方程、单元刚度矩阵的性质、特殊单元。

2. 重点难点重 点：一般单元的单元刚度矩阵。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

结点C
2.将上述过程用矩阵表示 （1）局部坐标系； 单元杆端位移、杆端内力等量 值以局部坐标系正向为正，反之 为负。 （2） 单元杆端可能的杆端位移和杆端力； （3）单元位移引起的杆端内力；
（5） 结点平衡：
可动结点劲度矩阵由相交于结点的各单元劲 度矩阵相应元素叠加求得。
（二） F 的建立：
1 2 3 4 5 6
（5）整体劲度矩阵 根据对号入座原则，叠加出整体劲度矩阵如下
1
2
3
4
5
6
K
1 96.389 2 0.0 EA 3 15.0 l1 4 88.889 5 0.0 6 0.0
1
0.0 11.852 0.0 5.268 11.852
单元绝对位
返回
§9—3 可动结点劲度矩阵
一、形成可动结点劲度矩阵的步骤
步骤： 1.对结构进行结点编号、单元标号、自由度编号： 2.确定单元杆端自由度序号（考虑约束条件）； 3.计算单元在局部坐标系中的劲度矩阵kmi 4.计算单元转换矩阵Ti 5.形成单元在整体坐标系中的劲度矩阵ki Ti kmi Ti
整体分析（如：力的平衡） 一般在整体坐标系中讨论 两种坐标系中杆端力，位移分量之间的关系——转换矩阵
整体坐标系中：
局部坐标系中：
写成矩阵形式：
其中：
称为平面固接单元的转换矩阵。 同理：
思考： 给出平面梁单元，平面铰单元的转换矩阵
四、单元在整体坐标系中的劲度矩阵
——整体坐标系
——局部坐标系
从局部坐标系出发，两边前乘
解：（1）建立坐标系和编号 单元划分、节点编号、节点位移或节点力编号，整体坐标系 及单元的局部坐标的方向如图2－21（b）所示。 （2）可动节点列阵为 （3）整体平衡方程
1 2 3 4 5 6
K FE
图2－21(b)
（4）各单元的劲度矩阵 ①各单元在局部坐标系中的劲度矩阵 ③ 由式（2－28）得 ①
五、单元劲度矩阵的性质 1、kmi ki 为对称矩阵
反力互等定理: k支座发生单位位移时在m支座内引起的反力，等于m支座发 生单位位移时在k支座内引起的反例。
2、kmi ki 为奇异矩阵
不存在，即已知 物理意义： 已知结点力列阵 移。 单元相对位移 可求出 ，反之，已知 无法求出对应的 。
限制刚体位移
0.0 15.0 -7.5 0.0 15.0 1 10 7.5 0.0 100.0 0.0 0.0 -100.0 0.0 11 2 EA 12 15.0 0.0 40.0 15.0 0.0 20.0 3 2 k③ 10 l1 4 7.5 0.0 15.0 7.5 0.0 15.0 4 5 0.0 100.0 0.0 0.0 100 0.0 5 6 0.0 20.0 －15.0 0.0 40.0 6 15.0
1.回顾位移法中求解FR1P 的过程： 作荷载弯矩图：
结点平衡 结点B： 结点C
2.将上述过程用矩阵表示： （1） 荷载引起的单元固端力： 单元1
单元2
单元3
FLi：单元固端力列阵。
(2)结点平衡：
结点B：
结点C：
结论：作用在单元上的荷载引起的等效荷载：由相交于结点的各单元 固端力列阵相应元素反号叠加求得。
F F F
① G ② G ③ G
0 60.0 40.0 0.0 60.0 40.0 0 20.0 22.5 0.0 20.0 22.5 0 0 0 0 0 0
再把 F 转换到整体坐标中，由
7 8
e G
F L F
e G T T
e G
得
1 2 3
9
F 60.0 0.0 40.0 60.0 0.0 40.0
3 12
-88.889 0.0 0.0 88.889 0.0 0.0
4 4
-5.268 11.852 11.852 17.78 0.0 0.0 5.268 11.852 11.852 35.556 0.0 0.0
5 6 5 6
1 2 3 2 10 4 5 6
五、解方程：
六、单元杆端力的计算：
位移法法中有叠加公式：
对杆端力写成矩阵形式：
Fmi ——局部坐标系中单元杆端内力列阵。
mi
——局部坐标系中单元杆端位移列阵。
由杆端内力画弯矩图、剪力图：
七、支座反力的计算：
由内力图：考虑支座结点平衡： 结点A： 结点B： 结点C： 结点D：
返回
§9—2 单元劲度矩阵
EI=20EA，试用矩阵位移法分析
图示的平面刚架。 解： 1.建立坐标系与编号
2.可动结点的位移列阵为
3.可动结点平衡方程
4，求
（1）计算个单元的方向余弦和杆长
(4)求
(5)求： （1）直接作用在结点上的荷载为
(2)作用在单元上的荷载
把FL沿整体坐标系方向分解，得
K
（1）计算机各单元的方向余弦和杆长：
（2）求 kmi
(3)求ki
单元（1）:Cx=0 Cy=1 杆长：l
同理：
（4）求 按照“对号入座“原则，由ki形成k哪
例如： 同理：
5.求：
对于桁架，一般只有结点荷 载，于是
得 6.求结点位移
7.求杆端力Fmi
8.求支座反力
例
设 EI=常数，EA=常数，
二、支座反力
求解步骤： 1，将Fmi 转换至整体坐标系中； 2.根据单元自由度序号列阵将杆端力Fi叠 加至支座反力列阵中。
返回
§9 —6
解：1.建立坐标系与编号 2.可动结点的位移列阵为
例题
例1 设EA=常数，试用矩阵位移法分析图示的平面桁架。
3.可动结点的平衡方程为
K F
4.求
k k
0.0 0.0 -100.0 0.0 0.0 100.0 0.0 7.5 15.0 0.0 -7.5 -15.0 15.0 40.0 0.0 15.0 20.0 ① EA 0.0 2 k ＝ 10 0.0 100.0 0.0 0.0 l1 100.0 0.0 0.0 7.5 15.0 0.0 7.5 15.0 0.0 -15.0 20.0 0.0 15.0 40.0 0.0 0.0 -100.0 0.0 0.0 100.0 0.0 5 .926 13.33 0.0 -5.926 -13.33 13.33 40.0 0.0 13.33 20.0 ② EA 0.0 2 k ＝ 10 0.0 0.0 100.0 0.0 0.0 l2 100.0 0.0 5.926 13.33 0.0 5.926 13.33 -13.33 20.0 0.0 13.33 40.0 0.0
1 2 3 4 5 6
1
2
3
4
5
6
k
②
88.889 0.0 1 0.0 5.268 2 0.0 11.852 EA 3 88.889 0.0 4 l1 5.268 5 0.0 11.852 6 0.0
1 2 10 11
0.0 11.852 35.556 0.0 11.852 17.78
②各单元在整体坐标系下得单元劲度矩阵
0 1 0 ① ③ LT LT ＝ 0 0 0 0 1 ② ，LT I 0 1 0 0 1 0 0 0 0 1 1 0
所以，由
k L kLT
T T
7
得
8 9 1 2 3
0.0 15.0 -7.5 0.0 15.0 1 7 7.5 2 8 0.0 100.0 0.0 0.0 -100.0 0.0 40.0 15.0 0.0 20.0 3 EA 9 15.0 0.0 ① 2 k ＝ 1 410 0.0 15.0 l1 7.5 0.0 15.0 7.5 2 0.0 100.0 0.0 0.0 100 0.0 5 6 3 15.0 0.0 20.0 15.0 0.0 40.0
2.非奇异矩阵
考虑了约束条件，排除了刚体位移
3.稀疏带状矩阵
只有临近结点之间才有相互影响
返回
§9—4 可动结点等效荷载列阵
一、直接作用在结点上的荷载
将结点集中荷载按自由度方向分解，将各荷载分量直接叠加到可 动结点荷载列阵中
二、作用在单元上的荷载
步骤： 1.求单元固端力； 2.转换至整体坐标系中； 3.按照单元杆端自由度序号叠加到可动结点等效荷载列阵中
第九章 矩阵位移法
§9-1 §9-2 §9-3 §9-4 §9-5 §9-6 矩阵位移法基本概念 单元劲度矩阵 可动结点劲度矩阵 可动结点等效荷载列阵 单元杆端力和支座反力 例题
§9-7
平面刚架计算程序
§9—1 矩阵位移法的基本概念
一、坐标系和符号规定 图示连续梁：
位移法求解基本系：
1.整体坐标系 x—y—z 2.结点位移、结点力等量值沿 坐标轴正向为正，反之为负。
例
解： （一）结点集中荷载
（二）单元荷载
1.求局部坐标单元固端力
2.转换到整体坐标
3.叠加
返回
§9—5 单元杆端内力和支座反力
一、单元杆端内力
1.计算公式
2.求解步骤 （1）形成单元局部坐标系下的单元劲度矩阵kmi （2）形成转换矩阵Ti
（3）形成杆端位移列阵 i
（4）形成固端力列阵FLi （5）计算单元最后杆端力， 先计算 在计算 或用 计算。
二、数字编号
1.结点编号 2.单元编号 3.结点位移编号
三、结点位移列阵
四、可动结点平衡矩阵方程
位移法典型方程
写成矩阵形式
可动结点平衡方程：