陕西省宝鸡市2013届高三3月份第二次模拟考试数学(文)试题

2013年宝鸡市高三教学质量检测（二）数学试卷分析一、命题思路：宝鸡市2013年高三质量检测（二）数学试题，遵照陕西省2013年《考试说明》的要求、体现《高中数学课程标准》精神，突出对基础知识、基本技能、基本思想方法和基本数学活动经验的考查，整套试卷从宏观上控制了难度，许多试题着力创新，如理科第7，8，9，10，14，18,20，21题。

同时，保持试题稳定性和前后两次的连续性，全卷几乎涵盖了60%以上知识点，对数列，三角，立几，概率统计，解几，函数等主干知识重点考查。

考查数学的应用意识，有利于培养学生分析和解决实际问题的能力。

以期能很好检测学生复习的效果，为教师改进教学和学生后期复习提供帮助。

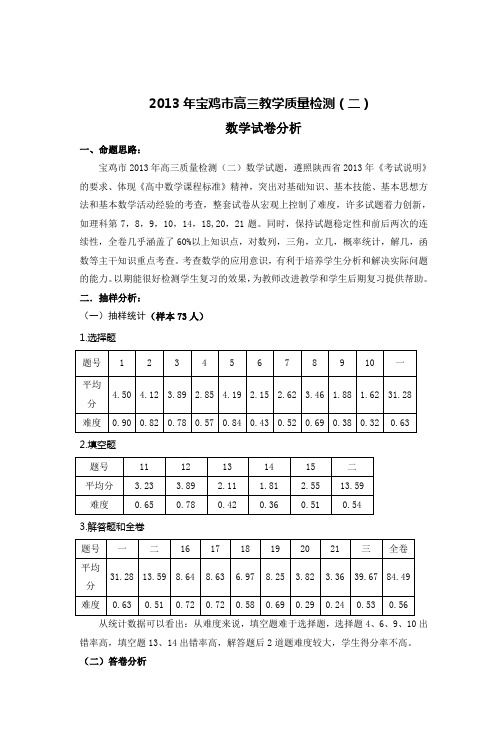
二．抽样分析：（一）抽样统计（样本73人）1.选择题2.填空题3.解答题和全卷从统计数据可以看出：从难度来说，填空题难于选择题，选择题4、6、9、10出错率高，填空题13、14出错率高，解答题后2道题难度较大，学生得分率不高。

（二）答卷分析第1题：理科以指数不等式解法，幂函数型的复合函数的值域为背景，考查集合的交、C xA By o图2并、补的运算。

错误点：（1）p集合中函数y =[0,1]，不是定义域；（2）U C M 求错，少一个等号，应是0x ≤；（３）集合的交、并、补的运算出错。

文科考查集合的交、并、补的运算，错误原因主要是集合运算出错。

第2题：文理同题。

考查圆的方程和相交弦的直线方程。

错误点：（1）圆心C 的坐标求错，应是(1,2)-；（2）没有理解圆的性质，即垂直与AB 直径的直线就是CP ；（3）CP 直线求错。

第3题：文理同题。

以数列背景考查程序框图知识。

错误点：（1）对输出S 的含义不理解，导致循环次数出错；（2）是和否弄反。

第4题：文理同题。

考查正切函数的对称点和坐标轴上的余弦值。

错误点：（1）正切函数t a n y x =图像的对称点是(,0),2k k Z π∈，学生写成(,0),k k Z π∈，漏掉(,0),2k k Z ππ+∈，导致cos θ只求出1±，漏掉cos 0θ=. 第5题：理科线面平行和垂直的判定和性质定理。

2022年陕西省宝鸡市高考文科数学二模试卷一.选择题：共计12小题，每小题5分，共60分1．（5分）若复数z 满足2z +z =3﹣2i ，其中i 为虚数单位，则z ＝（ ） A ．1+2iB ．1﹣2iC ．﹣1+2iD ．﹣1﹣2i2．（5分）已知全集为U ，集合A ，B 为U 的子集，若（∁U A ）∩B ＝∅，则A ∩B ＝（ ） A ．∁U BB ．∁U AC ．BD ．A3．（5分）“0＜m ＜2”是“方程x 2m+y 22−m=1表示焦点在x 轴上的椭圆”的（ ）A ．充要条件B ．.充分不必要条件C ．.必要不充分条件D ．.既不充分也不必要条件4．（5分）庄子说：一尺之锤，日取其半，万世不竭．这句话描述的是一个数列问题．现用程序框图描述，如图所示，若输入某个正数n 后，输出的S ∈(3132，127128)，则输入的n 的值为（ ）A ．7B ．6C ．5D ．45．（5分）设等比数列{a n }的前n 项和为S n ，若S 6S 3=3，则S 9S 6=（ ）A ．2B ．73C ．83D ．36．（5分）设m 、n 是两条不同的直线，α、β是两个不同的平面，给出下列四个命题： ①若m ⊥α，n ∥α，则m ⊥n ； ②若m ∥n ，n ∥α，则m ∥α； ③若m ∥n ，n ⊥β，m ∥α，则α⊥β；④若m ∩n ＝A ，m ∥α，m ∥β，n ∥α，n ∥β，则α∥β． 其中真命题的个数是（ ） A ．1B ．2C ．3D ．47．（5分）若变量x ，y 满足条件{x −y ≤0x −2y +2≥0x ≥−2，则目标函数z ＝x +y 的最小值为（ ）A ．﹣6B ．﹣2C ．﹣4D ．48．（5分）设函数f(x)=sin(2x −5π6)，将函数f （x ）的图象向左平移φ（φ＞0）个单位长度，得到函数g （x ）的图象，若g （x ）为偶函数，则φ的最小值是（ ） A ．π6B ．π3C ．2π3D ．5π69．（5分）北京2022年冬奥会吉祥物“冰墩墩”和冬残奥会吉祥物“雪容融”一亮相，好评不断，这是一次中国文化与奥林匹克精神的完美结合，现工厂决定从20只相同的“冰墩墩”，15只相同的“雪容融”和10个相同的北京2022年冬奥会徽章中，采取分层抽样的方法，抽取一个容量为n 的样本进行质量检测，若“冰墩墩”抽取4只，则n 为（ ） A ．3B ．2C ．5D ．910．（5分）已知直线y ＝x +a 与曲线y =√2−x 2的两个不同的交点，则实数a 的取值范围是（ ） A ．（﹣2，2）B ．（0，2）C ．(√2，2)D ．[√2，2)11．（5分）已知x ＞0，y ＞0，lg 2x +lg 8y ＝lg 2，则1x+13y 的最小值是（ ）A ．4B ．2√2C ．2D ．2√312．（5分）定义方程f （x ）＝f ′（x ）的实根x 0叫做函数f （x ）的“新驻点”，其中f ′（x ）是函数f （x ）的导函数．若函数g （x ）＝xe x +1，h （x ）＝lnx +1，φ（x ）＝x 3﹣1的“新驻点”分别为a ，b ，c ，则a ，b ，c 的大小是（ ）A ．a ＞b ＞cB ．c ＞a ＞bC ．c ＞b ＞aD ．b ＞c ＞a二.填空部分：每小题5分，共计4小题，总计20分13．（5分）已知平面向量a →，b →满足a →=（1，√3），|b →|＝3，a →⊥（a →−b →），则a →与b →夹角的余弦值为 ．14．（5分）函数f(x)=log 12(x 2−ax +3a)在区间[2，+∞）上是减函数，则实数a 的取值范围是 ．15．（5分）已知数列{a n }中，a 1＝1，a n ＞0，前n 项和为S n ．若a n =√S n +√S n−1(n ∈N ∗，n ≥2），则数列{1a n a n+1}的前15项和为 ．16．（5分）已知双曲线C ：x 2a 2−y 2b 2=1（a ＞0，b ＞0）的左、右焦点分别为F 1，F 2，过F 1的直线与C 的两条渐近线分别交于A ，B 两点．若F 1A →=AB →，F 1B →•F 2B →=0，则C 的离心率为 ．三.解答部分：共计6小题，共计70分，除二选一10分外，其余每小题12分17．（12分）函数f （x ）＝2sin （ωx +φ）+1（ω＞0，|φ|＜π2）的图像过点(π3，1)，且相邻对称轴间的距离为π2．（1）求ω，φ的值；（2）已知△ABC 的内角A ，B ，C 所对边为a ，b ，c ，若f(A2)=3，且a ＝2，求△ABC 的面积最大值；18．（12分）近年来，随之物质生活水平的提高以及中国社会人口老龄化加速，家政服务市场规模逐年增长，下表为2017年﹣2021年中国家政服务市场规模及2022年家政服务规模预测数据（单位：百亿元） 年份 2017 2018 2019 2020 2021 2022 市场规模3544587088100（1）若2017﹣2021年对应的代码依次为1﹣5，根据2017年﹣2021年的数据，用户规模y 关于年度代码的线性回归方程y =b x +a ；（2）把2022年的年代代码6代入（1）中求得回归方程，若求出的用户规模与预测的用户规模误差上下不超过5%，则认为预测数据符合模型，试问预测数据是否符合回归模型？ 参考数据：y=59，∑ 5i=1x i y i ＝1017，参考公式：b=∑ n i=1x i y i −nxy ∑ ni=1x i 2−nx2，a =y −b x ．19．（11分）如图所示，平面P AB ⊥平面ABCD ，底面ABCD 是边长为8的正方形，∠APB ＝90°，点E ，F 分别是DC ，AP 的中点． （1）证明：DF ∥平面PBE ；（2）若AB ＝2P A ，求四棱锥P ﹣ABED 的体积．20．（10分）已知曲线C 上任意一点到F （3，0）距离比它到直线x ＝﹣5的距离小2，经过点F （3，0）的直线l 的曲线C 交于A ，B 两点． （1）求曲线C 的方程；（2）若曲线C 在点A ，B 处的切线交于点P ，求△P AB 面积最小值．21．（10分）已知函数f （x ）＝ax ﹣1﹣e x ，其中a ∈R ．e ＝2.718⋯为自然对数的底数． （1）讨论函数的单调性；（2）若方程f （x ）＝xlnx 对x ∈（1，e ）有实根，求a 的取值范围．22．（10分）在直角坐标系xOy 中，曲线C 的参数方程为{x =2+sinα+cosα，y =cosα−sinα（α为参数）．以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，直线l 的方程为θ＝β（0＜β＜π2，ρ∈R ）． （1）求曲线C 的普通方程；（2）若曲线C 与直线l 交于A ，B 两点，且|OA |+|OB |＝3，求直线l 的斜率． 23．已知函数f （x ）＝lg （|x ﹣m |+|x ﹣2|﹣3）（m ∈R ）． （1）当m ＝1，求函数f （x ）的定义域；（2）若不等式f （x ）≥0对于R 恒成立，求实数m 的取值范围．2022年陕西省宝鸡市高考文科数学二模试卷参考答案与试题解析一.选择题：共计12小题，每小题5分，共60分1．（5分）若复数z 满足2z +z =3﹣2i ，其中i 为虚数单位，则z ＝（ ） A ．1+2iB ．1﹣2iC ．﹣1+2iD ．﹣1﹣2i【解答】解：复数z 满足2z +z =3﹣2i ， 设z ＝a +bi ，可得：2a +2bi +a ﹣bi ＝3﹣2i ． 解得a ＝1，b ＝﹣2． z ＝1﹣2i ． 故选：B ．2．（5分）已知全集为U ，集合A ，B 为U 的子集，若（∁U A ）∩B ＝∅，则A ∩B ＝（ ） A ．∁U BB ．∁U AC ．BD ．A【解答】解：因为（∁U A ）∩B ＝∅，所以B ⊆A ， 所以A ∩B ＝B ． 故选：C ．3．（5分）“0＜m ＜2”是“方程x 2m+y 22−m=1表示焦点在x 轴上的椭圆”的（ ）A ．充要条件B ．.充分不必要条件C ．.必要不充分条件D ．.既不充分也不必要条件 【解答】解：若方程x 2m+y 22−m=1表示焦点在x 轴上的椭圆，则{m ＞02−m ＞0m ＞2−m，解得1＜m ＜2，所以“0＜m ＜2”是“方程 x 2m+y 22−m=1表示焦点在x 轴上的椭圆“的必要不充分条件． 故选：C ．4．（5分）庄子说：一尺之锤，日取其半，万世不竭．这句话描述的是一个数列问题．现用程序框图描述，如图所示，若输入某个正数n后，输出的S∈(3132，127128)，则输入的n的值为（）A．7B．6C．5D．4【解答】解：框图首先给累加变量S赋值0，给循环变量k赋值0，输入n的值后，执行循环体，S=12，k＝1；判断1＞n不成立，执行循环体，S=34，k＝2；判断2＞n不成立，执行循环体，S=78，k＝3；判断3＞n不成立，执行循环体，S=1516，k＝4；判断4＞n不成立，执行循环体，S=3132，k＝5；判断5＞n不成立，执行循环体，S=6364，k＝6；判断6＞n不成立，执行循环体，S=127128，k＝7；…由于输出的S∈(3132，127128)，可得：当S=6364，k＝6时，应该满足条件6＞n，即：5≤n＜6，可得输入的正整数n 的值为5． 故选：C ．5．（5分）设等比数列{a n }的前n 项和为S n ，若S 6S 3=3，则S 9S 6=（ ）A ．2B ．73C ．83D ．3【解答】解：设公比为q ，则S 6S 3=a 1(1−q 6)1−q a 1(1−q 3)1−q=1−q 61−q =1+q 3＝3，所以q 3＝2， 所以S 9S 6=1−q 91−q =1−231−2=73．故选：B ．6．（5分）设m 、n 是两条不同的直线，α、β是两个不同的平面，给出下列四个命题： ①若m ⊥α，n ∥α，则m ⊥n ； ②若m ∥n ，n ∥α，则m ∥α； ③若m ∥n ，n ⊥β，m ∥α，则α⊥β；④若m ∩n ＝A ，m ∥α，m ∥β，n ∥α，n ∥β，则α∥β． 其中真命题的个数是（ ） A ．1B ．2C ．3D ．4【解答】解：对于①，假设n ⊂β，α∩β＝l ，因为n ∥α，所以n ∥l ，又m ⊥α， 所以m ⊥l ，而n ∥l ，所以m ⊥n ，正确；对于②，若m ∥n ，n ∥α，则m ∥α或m ⊂α，故错误；对于③，若m ∥n ，n ⊥β，则m ⊥β，又m ∥α，所以在平面α内一定存在一条直线l ，使m ∥l ，而m ⊥β，所以l ⊥β，l ⊂α，则α⊥β，正确；对于④，由面面平行的判定定理，可以判断出是正确的． 故真命题有3个． 故选：C ．7．（5分）若变量x ，y 满足条件{x −y ≤0x −2y +2≥0x ≥−2，则目标函数z ＝x +y 的最小值为（ ）A ．﹣6B ．﹣2C ．﹣4D ．4【解答】解：由约束条件作出可行域如图，联立{x =−2x −y =0，解得A （﹣2，﹣2），由z ＝x +y ，得y ＝﹣x +z ，由图可知，当直线y ＝﹣x +z 过A 时， 直线在y 轴上的截距最小，z 有最小值为﹣4． 故选：C ．8．（5分）设函数f(x)=sin(2x −5π6)，将函数f （x ）的图象向左平移φ（φ＞0）个单位长度，得到函数g （x ）的图象，若g （x ）为偶函数，则φ的最小值是（ ） A ．π6B ．π3C ．2π3D ．5π6【解答】解：函数f(x)=sin(2x −5π6)，将函数f （x ）的图象向左平移φ（φ＞0）个单位长度，得到函数g （x ）＝sin （2x +2φ−5π6）的图象． 若g （x ）为偶函数，则2φ−5π6=k π+π2，k ∈Z ， 令k ＝﹣1，求得φ的最小值为π6，故选：A ．9．（5分）北京2022年冬奥会吉祥物“冰墩墩”和冬残奥会吉祥物“雪容融”一亮相，好评不断，这是一次中国文化与奥林匹克精神的完美结合，现工厂决定从20只相同的“冰墩墩”，15只相同的“雪容融”和10个相同的北京2022年冬奥会徽章中，采取分层抽样的方法，抽取一个容量为n 的样本进行质量检测，若“冰墩墩”抽取4只，则n 为（ ） A ．3B ．2C ．5D ．9【解答】解：根据分层抽样的定义可得：420=n 20+15+10，解得n ＝9．故选：D ．10．（5分）已知直线y＝x+a与曲线y=√2−x2的两个不同的交点，则实数a的取值范围是（）A．（﹣2，2）B．（0，2）C．(√2，2)D．[√2，2)【解答】解：曲线y=√2−x2线是以（0，0）为圆心，√2为半径位于x轴上方的半圆．当直线l过点A（−√2，0）时，直线l与曲线有两个不同的交点，此时0=−√2+a，解得a=√2．当直线l与曲线相切时，直线和圆有一个交点，圆心（0，0）到直线x﹣y+a＝0的距离d=2=√2解得a＝2或﹣2（舍去），若曲线C和直线l有且仅有两个不同的交点，则直线l夹在两条直线之间，因此√2≤a＜2，故选：D．11．（5分）已知x＞0，y＞0，lg2x+lg8y＝lg2，则1x +13y的最小值是（）A．4B．2√2C．2D．2√3【解答】解：lg2x+lg8y＝lg2x+lg23y＝（x+3y）lg2，又由lg2x+lg8y＝lg2，则x+3y＝1，进而由基本不等式的性质可得，1 x +13y=（x+3y）（1x+13y）＝2+3yx+x3y≥4，故选：A．12．（5分）定义方程f（x）＝f′（x）的实根x0叫做函数f（x）的“新驻点”，其中f′（x）是函数f（x）的导函数．若函数g（x）＝xe x+1，h（x）＝lnx+1，φ（x）＝x3﹣1的“新驻点”分别为a，b，c，则a，b，c的大小是（）A．a＞b＞c B．c＞a＞b C．c＞b＞a D．b＞c＞a【解答】解：∵函数g（x）＝xe x+1，g'（x）＝xe x+e x，∴a为xe x+1＝xe x+e x的根，解得x＝0，即a＝0．∵h（x）＝lnx+1，h′（x）=1x，∴b为lnx+1=1x的根，可得x＝1，即可b＝1，∵φ（x ）＝x 3﹣1，φ'（x ）＝3x 2，∴c 为x 3﹣1＝3x 2的根，即函数φ1（x ）＝x 3﹣1﹣3x 2的零点，∵φ1′（x ）＝3x 2﹣6x ＝3x （x ﹣2），∴当x ∈（0，2）时，φ1′（x ）＜0，函数单调递减，当x ∈（﹣∞，0）∪（2，+∞）时，φ1′（x ）＞0，函数单调递增，又∵φ1（0）＜0，φ1（2）＜0，φ1（4）＞0，∴c ∈（2，4）， ∴c ＞b ＞a ． 故选：C ．二.填空部分：每小题5分，共计4小题，总计20分13．（5分）已知平面向量a →，b →满足a →=（1，√3），|b →|＝3，a →⊥（a →−b →），则a →与b →夹角的余弦值为23．【解答】解：|a →|=2，|b →|=3； ∵a →⊥(a →−b →)；∴a →⋅(a →−b →)=a →2−a →⋅b →=4−6cos ＜a →，b →＞=0； ∴cos ＜a →，b →＞=23． 故答案为：23．14．（5分）函数f(x)=log 12(x 2−ax +3a)在区间[2，+∞）上是减函数，则实数a 的取值范围是 （﹣4，4] ．【解答】解：设t ＝x 2﹣ax +3a ，则y ＝log 12t 为减函数，则若f （x ）在区间[2，+∞）上是减函数，则满足t ＝x 2﹣ax +3a ，在区间[2，+∞）上是增函数且t ＞0恒成立，即{−−a2≤24−2a +3a ＞0得{a ≤4a ＞−4， 得﹣4＜a ≤4，即实数a 的取值范围是（﹣4，4]， 故答案为：（﹣4，4]15．（5分）已知数列{a n }中，a 1＝1，a n ＞0，前n 项和为S n ．若a n =√S n +√S n−1(n ∈N ∗，n ≥2），则数列{1a n a n+1}的前15项和为 1531． 【解答】解：数列{a n }中，a 1＝1，a n ＞0，前n 项和为S n ．若a n =√S n +√S n−1(n ∈N ∗，n ≥2），则S n −S n−1=√S n +√S n−1，整理得√n −√S n−1=1，所以数列{√S n }是以1为首项，1位公差的等差数列， 则√S n =1+(n −1)=n ，所以a n ＝S n ﹣S n ﹣1＝2n ﹣1． 所以1a n a n+1=1(2n−1)(2n+1)=12(12n−1−12n+1)．所以T 15=12(1−13+13−15+⋯+129−131)=1531． 故答案为：1531．16．（5分）已知双曲线C ：x 2a −y 2b =1（a ＞0，b ＞0）的左、右焦点分别为F 1，F 2，过F 1的直线与C 的两条渐近线分别交于A ，B 两点．若F 1A →=AB →，F 1B →•F 2B →=0，则C 的离心率为 2 ． 【解答】解：如图，∵F 1A →=AB →，∴A 为F 1B 的中点，且O 为F 1F 2的中点， ∴AO 为△F 1F 2B 的中位线，又∵F 1B →⋅F 2B →=0，∴F 1B ⊥F 2B ，则OB ＝F 1O ＝c ． 设B （x 1，y 1），A （x 2，y 2）， ∵点B 在渐近线y =ba x 上， ∴{x 12+y 12=c 2y 1=ba x 1，得{x 1=a y 1=b ．又∵A 为F 1B 的中点，∴{x 2=−c+a2y 2=b2， ∵A 在渐近线y =−b ax 上， ∴b2=−b a⋅a−c 2，得c ＝2a ，则双曲线的离心率e =ca =2．故答案为：2．三.解答部分：共计6小题，共计70分，除二选一10分外，其余每小题12分17．（12分）函数f （x ）＝2sin （ωx +φ）+1（ω＞0，|φ|＜π2）的图像过点(π3，1)，且相邻对称轴间的距离为π2．（1）求ω，φ的值；（2）已知△ABC 的内角A ，B ，C 所对边为a ，b ，c ，若f(A2)=3，且a ＝2，求△ABC 的面积最大值；【解答】解：（1）∵相邻对称轴间的距离为π2．∴2πω=π，∴ω＝2，∴f （x ）＝2sin （2x +φ）+1，∵f （x ）的图像过点(π3，1)，∴2sin （2×π3+φ）+1＝1，∴sin （2×π3+φ）＝0， ∴φ=−2π3+k π，k ∈Z ，又|φ|＜π2，∴φ=π3；（2）由（1）知f （x ）＝2sin （2x +π3）+1，又f(A2)=3， ∴2sin （A +π3）+1＝3，∴sin （A +π3）＝1， 又π3＜A +π3＜4π3，∴A +π3=π2，∴A =π6， 在△ABC 中，由余弦定理有a 2＝b 2+c 2﹣2bc cos A ，∴4≥2bc −√3bc ， ∴bc ≤2−3=8+4√3，当且仅当b ＝c 时取等号， ∴△ABC 的面积最大值为S =12×（8+4√3）sinπ6=2+√3．18．（12分）近年来，随之物质生活水平的提高以及中国社会人口老龄化加速，家政服务市场规模逐年增长，下表为2017年﹣2021年中国家政服务市场规模及2022年家政服务规模预测数据（单位：百亿元） 年份2017201820192020 2021 2022市场规模3544587088100（1）若2017﹣2021年对应的代码依次为1﹣5，根据2017年﹣2021年的数据，用户规模y关于年度代码的线性回归方程y=b x+a；（2）把2022年的年代代码6代入（1）中求得回归方程，若求出的用户规模与预测的用户规模误差上下不超过5%，则认为预测数据符合模型，试问预测数据是否符合回归模型？参考数据：y=59，∑5i=1x i y i＝1017，参考公式：b=∑ni=1x i y i−nxy∑n i=1x i2−nx2，a=y−b x．【解答】解：（1）由表中的数据可得，x=15×(1+2+3+4+5)=3，y=59，∑5i=1x i2=55，∑5i=1x i y i＝1017，故b=∑ni=1x i y i−nxy∑n i=1x i2−nx2=1017−5×3×3955−5×32=13.2，a=y−b x=59﹣13.2×3＝19.4，故y=13.2x+19.4．（2）当x＝6时，y=13.2×6+19.4=98.6，∵|98.6﹣100|＜100×5%，∴认为预测数据符合模型．19．（11分）如图所示，平面P AB⊥平面ABCD，底面ABCD是边长为8的正方形，∠APB ＝90°，点E，F分别是DC，AP的中点．（1）证明：DF∥平面PBE；（2）若AB＝2P A，求四棱锥P﹣ABED的体积．【解答】（1）证明：设G是PB的中点，连接FG，EG，由于F 是P A 中点，所以FG ∥AB ，FG =12AB ， 由于E 是CD 的中点，所以DE ∥AB ，DE =12AB ， 所以FG ∥DE ，FG ＝DE ，则四边形DEGF 是平行四边形， 所以DF ∥EG ，因为DF ⊄平面PBE ，EG ⊂平面 PBE ， 所以DF ∥平面PBE ．（2）由于AB ＝2P A ＝8，所以PA =4，PB =√82−42=4√3， 过P 作PH ⊥AB ，交AB 于H ，由于平面P AB ⊥平面ABCD ，PH ⊂平面ABCD ，且交线为AB ， 所以PH ⊥平面ABCD ， 由12×AB ×PH =12×PA ×PB ⇒PH =2√3，直角梯形ABED 的面积为4+82×8=48，所以V P−ABED =13×48×2√3=32√3． 20．（10分）已知曲线C 上任意一点到F （3，0）距离比它到直线x ＝﹣5的距离小2，经过点F （3，0）的直线l 的曲线C 交于A ，B 两点． （1）求曲线C 的方程；（2）若曲线C 在点A ，B 处的切线交于点P ，求△P AB 面积最小值．【解答】解：（1）由题意知曲线C 上任意一点到F （3，0）距离与它到直线x ＝﹣3的距离相等，由抛物线的定义可知，曲线C 的方程为y 2＝12x ． （2）设点P （x 0，y 0），A （y 1212，y 1），B （y 2212，y 2），由题设直线l 的方程为my ＝x ﹣3，联立方程{my =x −3y 2=12x ，消去x 得y 2﹣12my ﹣36＝0，则y 1+y 2＝12m ，y 1y 2＝﹣36，由y 2＝12x 得2yy ′＝12，即y ′=6y ，则切线AP 的方程为y ﹣y 1=6y 1（x −y 1212），即为y =6y 1x +y 12，同理切线BP 的方程为y =6y 2x +y 22， 把点P （x 0，y 0），代入切线AP ，BP 方程得{y 0=6y 1x 0+y12y 0=6y 2x 0+y 22，解得{x 0=y 1y212y 0=y 1+y 22，则P （y 1y 212，y 1+y 22），即P （﹣3，6m ）， 点P （﹣3，6m ）到直线l ：x ﹣my ﹣3＝0的距离d =2√m +1=5√m 2+1，线段|AB |=√(m 2+1)[(y 1+y 2)2−4y 1y 2]=√(m 2+1)(144m 2+144)=12（m 2+1），S △P AB =12|AB |d ＝36（m 2+1）√m 2+1=36（m 2+1）32，故当m ＝0时，△P AB 面积有最小值36．21．（10分）已知函数f （x ）＝ax ﹣1﹣e x ，其中a ∈R ．e ＝2.718⋯为自然对数的底数． （1）讨论函数的单调性；（2）若方程f （x ）＝xlnx 对x ∈（1，e ）有实根，求a 的取值范围． 【解答】解：（1）f ′（x ）＝a ﹣e x ，当a ≤0时，f ′（x ）≤0恒成立，故函数f （x ）在R 上递减， 当a ＞0时，令f ′（x ）＞0， 解得x ＜lna ，故函数f （x ）在（﹣∞，lna ）递增，（lna ，+∞）递减， 综上所述，当a ≤0时，f （x ）在R 上递减，当a ＞0时，f （x ）在（﹣∞，lna ）递增，（lna ，+∞）递减； （2）由已知有：ax ﹣1﹣e x ＝xlnx 在（1，e ）有实数根， 参变分离可得：a =xlnx+e x +1x， 构造g （x ）=xlnx+e x +1x ，则g′(x)=(e x +1)(x−1)2，∵x ∈（1，e ），∴g ′（x ）＞0在（1，e ）恒成立， 故g （x ）在（1，e ）恒增，g(1)=e +1，g(e)=1+1e +e e−1， 故a 的取值范围是：(e +1，1+1e +e e−1)．22．（10分）在直角坐标系xOy 中，曲线C 的参数方程为{x =2+sinα+cosα，y =cosα−sinα（α为参数）．以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，直线l 的方程为θ＝β（0＜β＜π2，ρ∈R ）． （1）求曲线C 的普通方程；（2）若曲线C 与直线l 交于A ，B 两点，且|OA |+|OB |＝3，求直线l 的斜率．【解答】解：（1）曲线C 的参数方程为{x =2+sinα+cosα，y =cosα−sinα（α为参数），转换为普通方程为（x ﹣2）2+y 2＝2， （2）根据{x =ρcosθy =ρsinθx 2+y 2=ρ2，得把（x ﹣2）2+y 2＝2转换为极坐标方程为ρ2﹣4ρcos θ+2＝0；由于{ρ2−4ρcosθ+2=0θ=β，故ρ2﹣4ρcos β+2＝0， 所以ρ1+ρ2＝4cos β，ρ1ρ2＝2 故4cos β＝3；所以cosβ=34，sin β=√74； 故tanβ=√73； 故直线的斜率k =√73．23．已知函数f （x ）＝lg （|x ﹣m |+|x ﹣2|﹣3）（m ∈R ）． （1）当m ＝1，求函数f （x ）的定义域；（2）若不等式f （x ）≥0对于R 恒成立，求实数m 的取值范围． 【解答】解：（1）m ＝1时，函数f （x ）＝lg （|x ﹣1|+|x ﹣2|﹣3）， 令|x ﹣1|+|x ﹣2|﹣3＞0，则不等式等价于{x ＜1(1−x)+(2−x)−3＞0或{1≤x ≤2(x −1)+(2−x)−3＞0或{x ＞2(x −1)+(x −2)−3＞0， 解得x ＜0或无解或x ＞3，所以函数f （x ）的定义域为（﹣∞，0）∪（3，+∞）；（2）若不等式f （x ）≥0对于R 恒成立，则|x ﹣m |+|x ﹣2|﹣3≥1恒成立，即|x ﹣m |+|x ﹣2|≥4，因为|x ﹣m |+|x ﹣2|≥|（x ﹣m ）﹣（x ﹣2）|＝|2﹣m |， 所以不等式可化为|2﹣m |≥4，即|m ﹣2|≥4， 所以m ﹣2≤﹣4或m ﹣2≥4， 解得m ≤﹣2或m ≥6，所以m 的取值范围是（﹣∞，﹣2]∪[6，+∞）．。

高考模拟复习试卷试题模拟卷第01节 随机事件的概率A 基础巩固训练1.(·江西南昌检测)从装有2个红球和2个白球的口袋内任取2个球，那么互斥而不对立的两个事件是()A ．“至少有1个白球”和“都是红球”B ．“至少有1个白球”和“至多有1个红球”C ．“恰有1个白球”和“恰有2个白球”D ．“至多有1个白球”和“都是红球”[答案]C[解析] 该试验有三种结果：“恰有1个白球”“恰有2个白球”“没有白球”，故“恰有1个白球”和“恰有2个白球”是互斥事件且不是对立事件．2.(文)(·滨州模拟)在区间[0,1]上任取两个数a ，b ，则函数f(x)＝x2＋ax ＋b2无零点的概率为( )A ．12B ．23C ．34D ．14[答案] C3. 甲、乙两人喊拳，每人可以用手出0,5,10三个数字，每人则可喊0,5,10,15,20五个数字，当两人所出数字之和等于某人所喊数字时喊该数字者获胜，若甲喊10，乙喊15时，则 ()A ．甲胜的概率大B ．乙胜的概率大C ．甲、乙胜的概率一样大D ．不能确定谁获胜的概率大【答案】A4.(·赤峰模拟)先后抛掷硬币三次，则至少一次正面朝上的概率是( ) A.18B.38C.58D.78【答案】D【解析】至少一次正面朝上的对立事件的概率为18，故P ＝1－18＝78. 5.在一次随机试验中，彼此互斥的事件A ，B ，C ，D 的概率分别为0.2,0.2,0.3,0.3，则下列说法正确的是()A ．A ∪B 与C 是互斥事件，也是对立事件 B ．B ∪C 与D 是互斥事件，也是对立事件C ．A ∪C 与B ∪D 是互斥事件，但不是对立事件 D ．A 与B ∪C ∪D 是互斥事件，也是对立事件【答案】DB 能力提升训练1.(·济南调研)现釆用随机模拟的方法估计某运动员射击4次，至少击中3次的概率：先由计算器给出 0到9之间取整数值的随机数，指定0、1表示没有击中目标，2、3、4、5、6、7、8、9表示击中目标，以4个随机数为一组，代表射击4次的结果，经随机模拟产生了 20组随机数：7527 0293 7140 9857 0347 4373 8636 6947 1417 4698 0371 6233 2616 8045 6011 3661 9597 7424 7610 4281根据以上数据估计该射击运动员射击4次至少击中3次的概率为( )A ． 0.852B ． 0.8192C ．0.8D ． 0.75[答案] D[解析] 随机模拟产生的20组随机数，表示至少击中3次的组数为15，所以概率为P ＝1520＝0.75. 2.从1,2,3,4,5中随机抽三个不同的数，则其和为奇数的概率为( )A.15B.25C.35D.45【答案】B3. (·浙江台州中学统练)甲、乙两人玩猜数字游戏，先由甲心中想一个数字，记为a ，再由乙猜甲刚才所想的数字，把乙猜的数字记为b ，其中a 、b ∈{0,1,2,3,4,5}，若|a －b|≤1，则称甲乙“心相近”．现任意找两人玩这个游戏，则他们“心相近”的概率为( )A ．29B ．718C ．49D ．19[答案] C4. (威海市高三3月模拟考试)从集合{2,3,4,5}中随机抽取一个数a ，从集合{1,3,5}中随机抽取一个数b ，则向量(,)m a b =与向量(1,1)n =-垂直的概率为（A ）16（B ）13（C ）14（D ）12【答案】A【解析】由题意可知(,)m a b =有：(2,1),(2,3),(2,5),(3,1),(3,3),(3,5),(4,1),(4,3),(4,5),(5,1),(5,3),(5,5).共12个.m n ⊥即0,m n ⋅=所以1(1)0,a b ⨯+⨯-=即a b =，有(3,3)，(5,5)共2个满足条件.故所求概率为16. 5. 从一个三棱柱ABC －A1B1C1的六个顶点中任取四点，这四点不共面的概率是( ) A ．15 B ．25C ．35D ．45 [答案] D[解析] 从6个顶点中选4个，共有15种选法，其中共面的情况有三个侧面，∴概率P ＝15－315＝45.C 思维扩展训练1.(·安庆一模)将一颗骰子投掷两次，第一次出现的点数记为a ，第二次出现的点数记为b ，设两条直线l1：ax ＋by ＝2与l2：x ＋2y ＝2平行的概率为P1，相交的概率为P2，则点P(36P1,36P2)与圆C ：x2＋y2＝1 098的位置关系是()A ．点P 在圆C 上B ．点P 在圆C 外 C ．点P 在圆C 内D ．不能确定【答案】C2. 设集合A ＝{1,2}，B ＝{1,2,3}，分别从集合A 和B 中随机取一个数a 和b ，确定平面上的一个点P(a ，b)，记“点P(a ，b)落在直线x ＋y ＝n 上”为事件Cn(2≤n ≤5，n ∈N)，若事件Cn 的概率最大，则n 的所有可能值为()A ．3B ．4C ．2和5D ．3和4【答案】D【解析】P(a ，b)的个数为6个．落在直线x ＋y ＝2上的概率P(C2)＝16，若在直线x ＋y ＝3上的概率P(C3)＝26，落在直线x ＋y ＝4上的概率P(C4)＝26，落在直线x ＋y ＝5上的概率P(C5)＝16. 3. 某学校成立了数学、英语、音乐3个课外兴趣小组，3个小组分别有39、32、33个成员，一些成员参加了不止一个小组，具体情况如图所示．现随机选取一个成员，他属于至少2个小组的概率是________，他属于不超过2个小组的概率是________． 【答案】3513154. 已知某台纺纱机在1小时内发生0次、1次、2次断头的概率分别是0.8、0.12、0.05，则这台纺纱机在1小时内断头不超过两次的概率和断头超过两次的概率分别为__________，________.【答案】0.970.03【解析】断头不超过两次的概率P1＝0.8＋0.12＋0.05＝0.97.于是，断头超过两次的概率P2＝1－P1＝1－0.97＝0.03.5. 【雅安中学高三下期3月月考数学】(本小题满分12分)某产品的三个质量指标分别为x, y, z, 用综合指标S = x + y + z 评价该产品的等级. 若S≤4, 则该产品为一等品. 先从一批该产品中, 随机抽取10件产品作为样本, 其质量指标列表如下: 产品编号A1 A2 A3 A4 A5 质量指标(x, y, z)(1,1,2) (2,1,1) (2,2,2) (1,1,1) (1,2,1) 产品编号A6 A7 A8 A9 A10 质量指标(x, y, z) (1,2,2) (2,1,1) (2,2,1) (1,1,1) (2,1,2)(Ⅰ) (Ⅱ) 在该样品的一等品中, 随机抽取两件产品,(1) 用产品编号列出所有可能的结果;(2) 设事件B 为 “在取出的2件产品中, 每件产品的综合指标S 都等于4”, 求事件B 发生的概率高考模拟复习试卷试题模拟卷第03节 二项式定理一、选择题（本大题共12小题，每小题5分，在每小题给出的四个选择中，只有一个是符合题目要求的.）1．【“五个一名校联盟” 高三教学质量监测（一）5】在154)212(+x 的展开式中，系数是有理数的项共有 （ ）A.4项B.5项C.6项D.7项2．【宝鸡市高三数学质量检测（一）】若)21(3x x n -的展开式中第四项为常数项，则=n （ ） A . 4 B. 5 C. 6 D. 73．【改编题】6(1)(1)x x +-展开式中3x 项系数为（ ）A.14 B ．15 C ．16 D ．174．【金丽衢十二校高三第二次联考】二项式2111()x x -的展开式中，系数最大的项为（ ）A.第五项B.第六项C.第七项D.第六和第七项 5．【江西赣州市六校高三上学期期末联考】已知8a x x ⎛⎫- ⎪⎝⎭展开式中常数项为5670，其中a 是常数，则展开式中各项系数的和是( )A ．28B ．48C ．28或48D ．1或286．【高考陕西，理4】二项式(1)()n x n N ++∈的展开式中2x 的系数为15，则n =（ ） A ．4 B ．5 C ．6 D ．77．【高考新课标1，理10】25()x x y ++的展开式中，52x y 的系数为( )（A ）10 （B ）20 （C ）30（D ）608.【高考湖北，理3】已知(1)n x +的展开式中第4项与第8项的二项式系数相等，则奇数项的二项式 系数和为（）A.122 B ．112 C ．102 D ．92 9．【咸阳市高考模拟考试试题（三）】若n x x )2(3+展开式中存在常数项,则n 的值可以是（ ）A ．8B ．9C ．10D ．1210．【潍坊市高三3月模拟考试】设0(sin cos )k x x dx π=-⎰，若8280128(1)...kx a a x a x a x -=++++，则1238...a a a a ++++=( )(A) 1 (B)0 (C)l (D)256 11．【浙江高考第5题】在46)1()1(y x ++的展开式中，记nm y x 项的系数为),(n m f ，则=+++)3,0(2,1()1,2()0,3(f f f f ） （ ）A.45B.60C.120D. 21012.【原创题】210(1)x x -+展开式中3x 项的系数为（ ）.A.210 B ．120 C ．90 D ．210二、填空题（本大题共4小题，每小题5分，共20分.把答案填在题中的横线上.）13．【大纲高考第13题】8x y y x ⎛⎫- ⎪ ⎪⎝⎭的展开式中22x y 的系数为. 14．【改编题】对任意实数x ，有423401234(1)(3)(3)(3)(3)x a a x a x a x a a -=+-+-+-+-，则3a 的值为.15．【高考四川，理11】在5(21)x -的展开式中，含2x 的项的系数是（用数字作答）.16．【高考新课标2，理15】4()(1)a x x ++的展开式中x 的奇数次幂项的系数之和为32，则a =__________．三、解答题 （本大题共4小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17．已知在332n x x ⎛- ⎪⎭的展开式中，第6项为常数项． (1)求n ；(2)求含x2的项的系数；(3)求展开式中所有的有理项．18．已知223)n x x 的展开式的二项式系数和比(31)n x -的展开式的二项式系数和大992.求在212nx x ⎛⎫- ⎪⎝⎭的展开式中， (1)二项式系数最大的项；(2)系数的绝对值最大的项．19．设(1－2x)2 013＝a0＋a1x ＋a2x2＋…＋a2 013x2 013 (x ∈R)．(1)求a0＋a1＋a2＋…＋a2 013的值；(2)求a1＋a3＋a5＋…＋a2 013的值；(3)求|a0|＋|a1|＋|a2|＋…＋|a2 013|的值．20．【第二次大联考数学江苏版】对于给定的函数()f x ，定义()n f x 如下：()0()C (1)n k k n k n n k k f x f x x n -==-∑，其中2n n ∈*N ≥，． （1）当()1f x =时，求证：()1n f x =；（2）当()f x x =时，比较2014(2013)f 与2013(2014)f 的大小；（3）当2()f x x =时，求()n f x 的不为0的零点．高考模拟复习试卷试题模拟卷第八章 直线与圆一．基础题组1.（重庆市巴蜀中学高三月考数学、文、1）若直线210ax y ++=与直线20x y +-=互相垂直，那么a 的值等于( )A ．1B ．13-C ．23-D ．2- 2.（文昌中学高三模拟考试、文、15）圆心在直线x －2y ＝0上的圆C 与y 轴的正半轴相切，圆C 截x 轴所得弦的长为23，则圆C 的标准方程为________________．3.（重庆市巴蜀中学高三月考数学、文、15）在平面直角坐标系xOy 中，以点)0,1(为圆心且与直线)(012R m m y mx ∈=---相切的所有圆中，半径最大的圆的标准方程为.4.（重庆市部分区县高三上学期入学考试、文、16）若实数c b a ,,成等差数列，点)0,1(-P 在动直线0:==+c by ax l 上的射影为M ，点)3,0(N ，则线段MN 长度的最小值是．二．能力题组1.(五校协作体高三上学期期初考试数学、文、9)曲线21y x =+在点（1，2）处的切线为l ，则直线l 上的任意点P 与圆22430x y x +++=上的任意点Q 之间的最近距离是（ ）A.4515-B.2515- C.51- D.2 2.(示范高中高三第一次联考、文、14）已知圆的方程为()2214x y +-=。

2015年某某省某某市高考数学三模试卷（文科）一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一个是符合题目要求的。

1．（5分）（2015•某某三模）已知集合A={0，1}，B={x|x2≤4}，则A∩B=（）A． {0，1} B． {0，1，2} C．{x|0≤x＜2} D．{x|0≤x≤2}考点：交集及其运算．专题：集合．分析：求出B中不等式的解集确定出B，找出A与B的交集即可．解答：解：由B中不等式变形得：（x﹣2）（x+2）≤0，解得：﹣2≤x≤2，即B=，∵A={0，1}，∴A∩B={0，1}．故选：A．点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．2．（5分）（2015•某某三模）若平面向量=（1，2），=（﹣2，y）且，则，则||=（） A． B． C． 2 D． 5考点：数量积判断两个平面向量的垂直关系．专题：平面向量及应用．分析：通过向量垂直数量积为0求出y，然后求解向量的模．解答：解：平面向量=（1，2），=（﹣2，y）且，则，可得﹣2+2y=0，解得y=1，||==．故选：B．点评：本题考查向量的数量积的应用，向量垂直体积的应用，考查计算能力．3．（5分）（2015•某某三模）设a，b为实数，命题甲：a＜b＜0，命题乙：ab＞b2，则命题甲是命题乙的（）A．充分不必要条件 B．必要不充分条件C．充要条件 D．既不充分也不必要条件考点：必要条件、充分条件与充要条件的判断．专题：简易逻辑．分析：根据充分必要条件的定义进行判断即可．解答：解：由a＜b＜0能推出ab＞b2，是充分条件，由ab＞b2，推不出a＜b＜0，不是必要条件，故选：A．点评：本题考查了充分必要条件，考查不等式问题，是一道基础题．4．（5分）（2015•某某三模）一个四棱锥的侧棱长都相等，底面是正方形，其主视图如图所示，该四棱锥侧面积等于（）A． 20 B． 5 C． 4（+1） D． 4考点：简单空间图形的三视图．专题：空间位置关系与距离．分析：由已知中的三视图，可知该几何体是一个以俯视图为底面的四棱锥，求出侧面的高后，计算各个侧面的面积，相加可得答案．解答：解：由已知中的三视图，可知该几何体是一个以俯视图为底面的四棱锥，其底面棱长为2，高h=2，故侧面的侧高为=，故该四棱锥侧面积S=4××2×=4，故选：D点评：本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．5．（5分）（2015•某某三模）若a＞1，则在同一坐标系中，函数f（x）=a﹣x与函数g（x）=log a x 的图象可能是（）A． B． C． D．考点：函数的图象．专题：函数的性质及应用．分析：根据a＞1，把函数等价变形：y=a﹣x=为指数函数且为减函数，再利用y=log a x 为对数函数，即可得到答案．解答：解：当a＞1时，y=a﹣x=为指数函数且为减函数，y=log a x为对数函数且为增函数，只有C符合，其它均不符合，故选：C．点评：本题考查的知识是对数函数的图象与性质，指数函数的图象与性质，熟练掌握底数与指数（对数）函数单调性的关系是解答本题的关键．6．（5分）（2015•某某三模）阅读如图所示程序图，如果输出i=5，那么在空白矩形框中应填入的语句为（）A． S=2*i B． S=2*i﹣1 C． S=2*i﹣2 D． S=2*i+4考点：程序框图．专题：图表型；算法和程序框图．分析：题目给出了输出的结果i=5，让我们分析矩形框中应填的语句，根据判断框中内容，即s＜10，我们模拟程序执行的过程，从而得到答案．解答：解：当空白矩形框中应填入的语句为S=2*i时，程序在运行过程中各变量的值如下表示：i S 是否继续循环循环前1 0/第一圈 2 5 是第二圈 3 6 是第三圈 4 9 是第四圈 5 10 否故输出的i值为：5，符合题意．故选：A．点评：本题考查了程序框图中的当型循环，当型循环是当条件满足时进入循环体，不满足条件算法结束，输出结果，属于基础题．7．（5分）（2015•某某三模）已知函数f（x）=，那么f（）的值为（）A．﹣ B．﹣ C． D．考点：函数的值．专题：函数的性质及应用．分析：由已知条件利用分段函数的性质得f（）=f（﹣1）=f（﹣）=sin（﹣）=﹣sin=﹣．解答：解：∵函数f（x）=，∴f（）=f（﹣1）=f（﹣）=sin（﹣）=﹣sin=﹣．故选：B．点评：本题考查函数值的求法，是基础题，解题时要认真审题，注意分段函数的性质的合理运用．8．（5分）（2015•某某三模）在某新型材料的研制中，实验人员获得了如下一组实验数据：现准备下列四个函数中的一个近似地表示这些数据的规律，其中最接近的一个是（）X 1.99 3 4 5.1 6.12Y 1.5 4.04 7.5 12 18.01 A． y=2x﹣1 B． log2x C． y= D． y=（）x考点：归纳推理．专题：函数的性质及应用；推理和证明．分析：由表中的数据分析得：自变量基本上是等速增加，相应的函数值增加的速度越来越快，结合基本初等函数的单调性，利用排除法可得出正确的答案．解答：解：由表格中的数据知，y随x的变化趋势，可得函数在（1，+∞）上是增函数，且y的变化随x的增大越来越快，∵A中函数是线性增加的函数，B中函数是比线性增加还缓慢的函数，D中函数是减函数；∴排除A，B、D答案，C中函数y=比较符合题意，故选：C．点评：本题考查函数模型的选择与应用问题，解题的关键是掌握各种基本初等函数，如一次函数，二次函数，指数函数，对数函数的图象与性质，是基础题．9．（5分）（2015•某某三模）把函数y=cos（﹣2x）的图象向右平移，得到函数f（x）的图象，则函数f（x）为（）A．周期为π的奇函数 B．周期为π的偶函数C．周期为2π的奇函数 D．周期为2π的偶函数考点：函数y=Asin（ωx+φ）的图象变换．专题：三角函数的图像与性质．分析：由条件利用诱导公式，函数y=Asin（ωx+φ）的图象变换规律，正弦函数的周期性、奇偶性，得出结论．解答：解：把函数y=cos（﹣2x）=cos（2x﹣）的图象向右平移，得到函数f（x）=cos=cos（2x﹣）=sin2x 的图象，由于f（x）是周期为π的奇函数，故选：A．点评：本题主要考查诱导公式，函数y=Asin（ωx+φ）的图象变换规律，正弦函数的周期性、奇偶性，属于基础题．10．（5分）（2007•某某）以双曲线的右焦点为圆心，且与其渐近线相切的圆的方程是（）A． x2+y2﹣10x+9=0 B． x2+y2﹣10x+16=0C． x2+y2+10x+16=0 D． x2+y2+20x+9=0考点：双曲线的简单性质．专题：计算题．分析：求出双曲线的右焦点得到圆心，在求出圆心到其渐近线的距离得到圆的半径，从而得到圆的方程．解答：解：右焦点即圆心为（5，0），一渐近线方程为，即4x﹣3y=0，，圆方程为（x﹣5）2+y2=16，即x2+y2﹣10x+9=0，故选A．点评：本题考查双曲线的焦点坐标和其渐近线方程以及圆的基础知识，在解题过程要注意相关知识的灵活运用．11．（5分）（2015•某某三模）某企业为节能减排，用9万元购进一台新设备用于生产．第一年需运营费用2万元，从第二年起，每年运营费用均比上一年增加2万元，该设备每年生产的收入均为11万元．设该设备使用了n（n∈N*）年后，年平均盈利额达到最大值（盈利额等于收入减去成本），则n等于（）A． 6 B． 5 C． 4 D． 3考点：函数模型的选择与应用．专题：计算题；等差数列与等比数列．分析：根据题意建立等差数列模型，利用等差数列的性质以及求和公式即可得到结论．解答：解：设该设备第n年的营运费为a n，万元，则数列{a n}是以2为首项，2为公差的等差数列，则a n=2n，则该设备使用了n年的营运费用总和为T n=n2+n，设第n年的盈利总额为S n，则S n=11n﹣（n2+n）﹣9=﹣n2+10n﹣9=﹣（n﹣5）2+16，∴当n=5时，S n取得最大值16，故选：B．点评：本题主要考查与数列有关的应用问题，根据条件利用等差数列的通项公式求出盈利总额的表达式是解决本题的关键．12．（5分）（2015•某某三模）设函数y=f（x）在区间（a，b）上的导函数为f′（x），f′（x）在区间（a，b）上的导函数为f″（x），若在区间（a，b）上f″（x）＜0恒成立，则称函数f（x）在区间（a，b）“凸函数“；已知f（x）=x4﹣x3﹣x2在（1，3）上为“凸函数”，则实数取值X围是（）A．（﹣∞，） B． C．（﹣∞，﹣2） D．=2=﹣m2+﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（8分）∵﹣≤m≤，即0≤m2≤2∴当m=0时，（|PA|2+|PB|2）max=，|PA|2+|PB|2的最大值为．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（10分）点评：本题考查椭圆的标准方程，考查直线与椭圆的位置关系，考查韦达定理的运用，考查学生的计算能力，属于中档题．20．（12分）（2015•某某三模）最近，X师傅和李师傅要将家中闲置资金进行投资理财．现有两种投资方案，且一年后投资盈亏的情况如下：（1）投资股市：投资结果获利不赔不赚亏损概率（2）购买基金：投资结果获利不赔不赚亏损概率p q（Ⅰ）当时，求q的值；（Ⅱ）已知“购买基金”亏损的概率比“投资股市”亏损的概率小，求p的取值X围；（Ⅲ）已知X师傅和李师傅两人都选择了“购买基金”来进行投资，假设三种投资结果出现的可能性相同，求一年后他们两人中至少有一人获利的概率．考点：相互独立事件的概率乘法公式；互斥事件的概率加法公式．专题：概率与统计．分析：（Ⅰ）由题意可得p++q=1，代入可得q值；（Ⅱ）由题意可得，再由p++q=1和概率的取值X围，解不等式可得；（Ⅲ）列举可得所有可能的投资结果有9种，事件A的结果有5种，由概率公式可得．解答：解：（Ⅰ）∵“购买基金”后，投资结果只有“获利”、“不赔不赚”、“亏损”三种，且三种投资结果相互独立，∴p++q=1，又∵，∴q=；（Ⅱ）∵由“购买基金”亏损的概率比“投资股市”亏损的概率小，∴，∵p++q=1，∴，解得，又∵，q≥0，∴，∴；（Ⅲ）记事件A为“一年后X师傅和李师傅两人中至少有一人获利”，用a，b，c分别表示一年后X师傅购买基金“获利”、“不赔不赚”、“亏损”，用x，y，z分别表示一年后李师傅购买基金“获利”、“不赔不赚”、“亏损”，则一年后X师傅和李师傅购买基金，所有可能的投资结果有3×3=9种，它们是：（a，x），（a，y），（a，z），（b，x），（b，y），（b，z），（c，x），（c，y），（c，z），∴事件A的结果有5种，它们是：（a，x），（a，y），（a，z），（b，x），（c，x）．∴这一年后X师傅和李师傅两人中至少有一人获利的概率点评：本题考查相互独立事件发生的概率，涉及列举法求基本事件数，属中档题．21．（12分）（2015•某某三模）已知函数f（x）=e x﹣ax﹣a（其中a∈R，e是自然对数的底数，e=2.71828…）．（Ⅰ）当a=e时，求函数f（x）的极值；（Ⅱ）若f（x）≥0恒成立，某某数a的取值X围；（Ⅲ）求证：对任意正整数n，都有××…×＞．考点：利用导数求闭区间上函数的最值；利用导数研究函数的单调性；利用导数研究函数的极值．专题：计算题；证明题；函数的性质及应用；导数的综合应用．分析：（Ⅰ）当a=e时，f（x）=e x﹣ex﹣e，f′（x）=e x﹣e，从而由导数的正负确定函数的单调性及极值；（Ⅱ）求导f′（x）=e x﹣a，从而讨论确定函数的单调性，由函数的单调性确定函数的最值，从而化恒成立问题为最值问题；（Ⅲ）由（Ⅱ）知，当a=1时，f（x）≥0恒成立，从而可化出ln（x+1）≤x，令x=（n∈N*），从而得到，从而证明．解答：解：（Ⅰ）当a=e时，f（x）=e x﹣ex﹣e，f′（x）=e x﹣e，当x＜1时，f′（x）＜0；当x＞1时，f′（x）＞0．所以函数f（x）在（﹣∞，1）上单调递减，在（1，+∞）上单调递增，所以函数f（x）在x=1处取得极小值f（1）=﹣e，函数f（x）无极大值．（Ⅱ）由f（x）=e x﹣ax﹣a，f′（x）=e x﹣a，若a＜0，则f′（x）＞0，函数f（x）单调递增，当x趋近于负无穷大时，f（x）趋近于负无穷大；当x趋近于正无穷大时，f（x）趋近于正无穷大，故函数f（x）存在唯一零点x0，当x＜x0时，f（x）＜0；当x＞x0时，f（x）＞0．故a＜0不满足条件．若a=0，f（x）=e x≥0恒成立，满足条件．若a＞0，由f′（x）=0，得x=lna，当x＜lna时，f′（x）＜0；当x＞lna时，f′（x）＞0，所以函数f（x）在（﹣∞，lna）上单调递减，在（lna，+∞）上单调递增，所以函数f（x）在x=lna处取得极小值f（lna）=﹣a•lna，由f（lna）≥0得﹣a•lna≥0，解得0＜a≤1．综上，满足f（x）≥0恒成立时实数a的取值X围是．（Ⅲ）证明：由（Ⅱ）知，当a=1时，f（x）≥0恒成立，所以f（x）=e x﹣x﹣1≥0恒成立，即e x≥x+1，所以ln（x+1）≤x，令x=（n∈N*），得，则有ln（1+）+ln（1+）+…+ln（1+）＜++…+=1﹣＜1，所以，所以，即．点评：本题考查了导数的综合应用及恒成立问题，难点在于证明不等式时函数的构造与化简，属于难题．四、选作题：请考生在22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分，作答时，用2B铅笔在答题卡上把所选题目对应的标号涂黑。

陕西省宝鸡市2013届高三数学第二次模拟考试（扫描版）北师大版数 学（文 理） 答 案一、选择题： 题号 1 2 3 4 5 6 7 8 9 10 理A D B A C B D A D C B 理B A B C D A B A D C B 文ABB AC B BD D A B 文B A BCDBBDCBB二、填空题：11．（理）（1，-2）；（文）-32 12.（理）2；（文）（1，-2） 13.【理】 6；【文】（0,1） 14．（理）2,6,18,54,166,；（文）89； 15. A. a ≥2(或[2,+∞)) B.23C. （2,1） 三、解答题： 16．（理科）解：（Ⅰ）设数列{a n }的公比为q(q ≠1)， 由题意得 241171q a q a q a += ， （1分） ∴247q q q +=,即27410q q q+=，∴S 4+S 7=q q a q q a --+--1)1(1)1(7141=q q q a ---1)2(741=q q a --1)22(101=qq a --1)1(2101=S 10 . （5分）∴S 4、S 10、S 7成等差数列. (6分)(Ⅱ)依题意得数列{|a 3n |}是首项为1，公比为|q 3|的等比数列,∴T n =||1||133q q n-- . (7分) 又由（Ⅰ）得247q q q +=，∴20136=--q q ，（8分）解得13=q (舍去)，3q =-21. (10分) ∴T n =|21|1|21|1----n=])21(1[2n -<2 . (12分) (文科) 解：（Ⅰ）由已知得6S 2=2S 1+4S 3，a 1=1，∴6(1+q)=2+4(1+q+q 2) .（2分）2q 2-q=0， q=21或q=0(舍去). （4分）∴a n =(21)n-1. (6分) （Ⅱ）由题意得2a n -b n =6-2n.（8分） b n =2a n +2n-6=2(21)n-1+2n-6,设数列{b n }的前n 项和为T n , T n =211])21(1[2--n +2)624(-+-n n . （10分） =n 2-5n+4-2)21(-n （12分）17．解：（（理）Ⅰ）由函数图象向左平移12π得到函数f(x)=Asin(ωx+ϕ)，(A>0,ω>0,|ϕ|<2π)的部分图象，由图象最高点得A=1，由周期21T=（127π+12π）-（12π+12π）=2π，T=π,∴ω=2. (2分) 当x=12π时,f(x)=1，可得 sin(2·12π+ϕ)=1,∵|ϕ|<2π，∴ ϕ=3π． ∴f(x)=sin(2x+3π) . (4分)由图象可得f(x)的单调减区间为[k π+12π,k π+127π],k ∈Z . (6分)（Ⅱ）由（I ）可知,sin(2A+3π)=1,∵0<A<π , ∴3π<2A+3π<37π , ∴2A+3π=2π, A=12π .∵0<B<π,∴sinB=B 2cos 1+=53. (9分)由正弦定理得BbA a sin sin =⇒b=)26(3+. (12分) (文科) 解：（Ⅰ）由题可知：f(x)=4sin ωx •2)2cos(1π+ω-x +cos2ωx=2sin ωx+1, （4分） 当ω=1时，f(x)=2sinx+1，则T=2π .(6分)（Ⅱ）由（Ⅰ）知：1sin 2)(+=x x f ω；欲使)(x f 在]32,2[ππ-上单调递增，则有[-2π,32π]⊆[-ωπ42,ωπ42]，∴-2π≥-ωπ42,32π≤ωπ42,∴0<ω≤43,于是ω∈(0,43] .(12分) 18.（理）解法1:(Ⅰ)∵ 四边形ABCD 为边长为菱形，∴AC ⊥BD 又∵B 1•=B 1)(•+=B B 11•+•而B B AB 1•=-B B BA 1•=-||||1B B BA cos60°=-3,∴B 1O ⊥平面ABCD, ∴平面B 1AC ⊥平面ABCD连接BC 1交B 1C 于E ，E 就为BC 1的中点.在△B 1OC 中，作EF ⊥OC,垂足为F ，连接BF ，则EF ∥B 1O ，EF ⊥平面ABCD ，（II ）依题意知，从乙校中选“高个子”的人数ξ的所有可能为0,1,2,3.P(ξ=0)=3834C C =141, P(ξ=1)=382414C C C =73,P(ξ=2)=381424C C C =73, P(ξ=3)=3834C C =141因此，ξ的分布列如下：ξ 0 1 2 3P 141 73 73 141 （10分）∵点P(1,1)是函数f(x)=lnx+21ax 2-(a+1)x 的图象上一点，∴21a-(a+1)=1,a=-4, f(x)=lnx-2x 2+3x. （2分） ∴)(x f '=x x x )14)(1(+- . （3分） x (0,1) 1 (1,+∞)4 +t =2成立.（13分）)(xf'+ 0 －)(xf↗ 1 ↘显然有h(t)>2恒成立. 所以在（1，+∞）内不存在,使得lnt+1综上所述，假设不成立.所以，函数f(x)不存在“中值相依切线”. （14分）。

2013年宝鸡市高三数学质量检测（一）数学（文科）试题本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，其中第Ⅱ卷第15考题为三选一，其它题为必考题，考生作答时，将答案写在答题卡上，在本试卷上答题无效．本试卷满分150分，考试时间120分钟． 注意事项：1． 答题前，务必将自己的姓名、准考证号填写在答题卡规定的位置上．2． 选择题答案使用2B 铅笔填涂，如需改动，用橡皮擦干净后，再选涂其它答案标号； 选择题答案使用0．5毫米的黑色中性（签字9笔或碳素笔书写，字体：工整、笔迹清楚，将答案书写在答题卡规定的位置上．3． 所有题目必须在答题卡上作答，在试卷上答题无效。

第Ⅰ卷 （选择题共50分）一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一个是符合题目要求的．1.复数,1i z -=则=+z z1（ ） A ．i 2123- B. i 2321- C. i 2323- D. i 2321+2.下列函数中，最小正周期为π，且图像关于直线3π=x 对称的是（ ）A. )32sin(π-=x y B )62sin(π-=x yC ．)62sin(π+=x y D )62sin(π+=x y 3.计算机是将信息转换成二进制数进行处理的。

二进制即“逢二进一”，如)1101(2表示二进制的数，将它转化成十进制的形式是130********222=⨯+⨯+⨯+⨯，那么将二进制1...11（共16位）转换成十进制数的形式是（ ） A ．2172- B.1172- C1162- D1152-4.若将集合P={1,2,3,4}，Q={0<x<5,x ∈R}，则下列论断正确的是（ ）A. x ∈P 是x ∈Q 的必要不充分条件B. x ∈P 是x ∈Q 的即不充分也不必要条件。

C. x ∈P 是x ∈Q 的充分必要条件D. x ∈P 是x ∈Q 的充分不必要条件 5.已知抛物线px y22=上一点M （1，m ）到其焦点的距离为5，则抛物线的准线方程为（ ）ACD俯视图主视图A. x=-4B. x=-8C. x=4D. x=86.已知P 是△ABC 所在平面内一点，→=→+→+→02PA PC PB ,现将一粒黄豆随机撒在△ABC 内，则黄豆落在△PBC 内的概率是（ ）A 41 B. 31 C 21 D 327.在三棱锥D-ABC 中，AC=BC=CD=2，CD ⊥平面ABC,90=∠ACB .若其主视图，俯视图如图所示，则其左视图的面积为（ ） A 2 B 2C3 D 68设函数在652231)(+++=x a x f x x 在区间[，1，]3上单调递增，则实数a 的取值范围（ ） A.]5,5[- B. ),5[+∞- C.,]3,(--∞ D.),5[]3,(+∞---∞ 9.设区间]1,0[是方程0)(=x f算法求出方程0)(=x f 在区间]1,0[上的一个 近似解的流程图如图，设a,b ∈]1,0[， 现要求精确度为ε，图中序号①，②处应填入的内容为（ ）A. 2;2ba b b a a +=+=B. 2;2ba ab a b +=+= C. 2;2ab b a ==D. 2;2ba ab ==10.在平面直角坐标系xoy 中，过动 点P 分别作圆12222:1=++++y x yxc 22yx c B 卷切线PA,PB (A,B 为切点)，若PB PA =，则OP 的最小值为（ ）A. 25B. 2C. 53D. 54第Ⅱ卷 （非选择题共100分）二、填空题：本大题共5小题，每小题5分，满分25分，把答案填在15题）11.统计某校1000名学生的数学会考成绩，得到样本频率分布直方图如右图所示，规定不低于60分为及格，不低于80分为优秀，则及格人数是 ；，优秀率 。

陕西省宝鸡市2013届高三第三次模拟考试数学（理）试题本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，其中第Ⅱ卷第l 5考题为三选一，其它题为必考题，考生作答时，将答案写在答题卡上，在本试卷上答题无效，本试卷满分1 50分，考试时间120分钟．注意事项：1．答题前，务必先将自己的姓名、准考证号填写在答题卡规定的位置上2．选择题答案使刚2B 铅笔填涂，如需改动，用橡皮擦干净后，再选涂其它答案标号；非选择题答案使用0’．5毫米的黑色中性（签字）笔或碳素笔书写，字体工整、笔迹清楚，将答案书写在答题卡规定的位置上． ‘’ ’3．所有题目必须在答题卡上作答，在斌卷上答题无效．参考公式：样本数据n x x x ,,,21 的标准差；x x x x x x x ns n 其中],)()()[(122221-+-+-= 为样本平均数； 柱体体积公式：为底面面积其中S Sh V ,=、h 为高； 锥体体积公式：h S Sh V ,,31为底面面积其中=为高； 球的表面积、体积公式：,34,432R V R S ππ==其中R 为球的半径。

第Ⅰ卷一、选择题（本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，’只有一项是符合题目要求的）：1．集合]},[,ln |{1e e x x y y P -∈==，集合M={a}，若PM P =，则a 的取值范围是 A ．[-1，1] B ．[1，+∞） C ．（-∞，-1] D ．（-∞，-1] [1，+∞）【答案】A【解析】集合{}1{|ln ,[,]}=x |11P y y x x e e x -==∈-≤≤，因为P M P =，所以11a -≤≤，因此选A 。

2．复数i i i i -++1432在复平面内对应的点与原点的距离为A ．1B ．2C ．2D ．2【答案】B 【解析】234-1-1-11===-11122i i i i i i i i i +++---，所以复数ii i i -++1432在复平面内对应的点11,22⎛⎫- ⎪⎝⎭2=。

试卷类型:A陕西省宝鸡中学2012-2013学年度高三数学（文）第一学期月考（二）说明：1.本试题分Ⅰ，Ⅱ卷，第Ⅰ卷的答案按照A ，B 卷的要求涂到答题卡 上，第Ⅰ卷不交；2.全卷共三大题21小题，满分150分，120分钟完卷。

第Ⅰ卷 （共50分）一.选择题（每题5分共50分） 1.已知}),3sin(|{},1,0,1{R x x y y Q p ∈+==-=π，则=⋂Q P （ ）A . QB . PC . }1,1{-D .}0,1{-2.函数x xx f 21)(+=在1=x 处切线的倾斜角为（ ）A . 4πB .6πC .3πD .32π3.将函数x y 2sin =的图像向左平移12π个单位，得到函数)20)(2sin(πϕϕ<<+=x y 的图像，则=ϕ（ ）A .3πB .12πC .4πD .6π4.已知A 是ABC ∆的内角，则“23sin =A ”是“3tan =A ”的（ ）A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件5.函数|2|ln )(--=x x x f 在定义域内零点个数为（ ）A .3B . 2C . 1D .06.若函数1)(23+++=mx x x x f 是R 上的单调函数，则实数m 的取值范围为（ ）A .]31(，-∞B .),31(+∞C .)31(，-∞D .),31[+∞7.已知ABC ∆中，45,2,1===B b a ，则角A 等于（ ）A .150 B .30 C .60 D .908.已知x x f sin :-→是集合])2,0[(π⊆A A 到集合}21,0{=B 的一个映射，则集合A 中的元素个数最多有（ ）9第题图A .4个B . 5个C .6个D .7个9. 函数()sin(),(,,f x A x A ωϕωϕ=+是常数，0,0,0)2A πωϕ>><<的部分图象如图所示，则,ωϕ的值为( )A .1,3πωϕ==B .1,3πωϕ==- C .2,3πωϕ==-D .2,3πωϕ==10.已知函数)()(R x ex f y x∈=满足)()('x f x f >，则)1(f 与)0(ef 的大小关系为（ ）A . )0()1(ef f =B .)0()1(ef f <C .)0()1(ef f >D .不能确定第Ⅱ卷（非选择题共100分）二．填空题（每题5分共25分）11.60cos 15sin 30cos 75sin ⋅-⋅ 的值为__________；12.若1log-=n m ，则m n +3的最小值为__________；13.设R m ∈，若函数)(2)(R x mx e x f x ∈+=有大于零的极值点，则m 的取值范围为__________；14.已知某生产厂家的年利润y （单位：万元）与年产量x （单位：万件）函数关系式为23481313-+-=x x y ，则使该生产厂家获取最大年利润的年产量为__________;15.给出下列命题：①“2=x ”是“42=x ”的充分不必要条件；②设}|{},3|{2t x y y B x x A +-==≤= ，若φ=⋂B A ，则实数t 的取值范围为),3[+∞；③若22loglog2≥+xx ，则1>x ；④存在R y x ∈,，使y x y x sin sin )sin(-=-；⑤若命题P ：对任意的R x ∈，函数)32cos(π-=x y 的递减区间为)](125,12[Z k k k ∈+-ππππ，命题q ：存在,R x ∈使1tan =x ，则命题“p 且q ”是真命题. 其中真命题的序号为__________.三.解答题(写出文字说明、证明过程或演算步骤,本大题共6小题，共75分)16. (12分)已知二次函数))(R x x f y ∈=（的图像过点)3,0(-，且0)(>x f 的解集为)3,1(. （1）求)(x f 的解析式； （2）求函数]2,0[),(sin π∈=x x f y 的最大值与最小值.17.(12分)已知),0(,55)2sin(πααπ∈-=+.（1）求)3cos()sin()23cos()2sin(απαπαππα++-+--的值；（2）求)42sin(πα+的值.18.(12分)已知命题P ：函数)10)(21(log )(≠>-=a a x x f a 且在定义域上单调递增；命题Q ：不等式04)2(2)2(2<--+-x a x a 对任意实数x 恒成立.若P 或Q 是真命题，求实数a 的取值范围.19.(12分)已知向量)sin ,(sin x x a =，))(sin ,(cos R x x x b ∈=， 若函数b a x f ⋅=)(. （1）求)(x f 的最小正周期； （2）若]2,0[π∈x ，求)(x f 的最大值及相应的x 值；（3）若],0[π∈x ，求)(x f 的单调递减区间.20.(13分)已知函数x bx ax x f 2)(23++=在1-=x 及2=x 处取得极值.（1）求b a ,的值；（2）若关于x 的方程02)(23=+--+t x x x x f 在区间]2,21[上恰有两个不相等的实数根，求实数t 的取值范围.21.(14分)已知函数)0(2331)(23>+-=m mx mxx x f .（1）当2=m 时，求曲线)(x f y =在点)0,0(处的切线方程； （2）讨论函数)(x f y =的单调性；（3）若函数)(x f 既有极大值，又有极小值，且当m x 40≤≤时，332)323()(22+-+≤x m m mxx f 恒成立，求实数m 的取值范围.参考答案一．选择题A 卷：BADBB DBBDC 二．填空题 11.22; 12.32 ；13.），（21-∞-；14.9万件；15.①③④三．解答题：16.解：（1）由已知设)3)(1()(--=x x a x f ，又)(x f 的图像过点)3,0(-，即3)0(--f ，所以1-=a ，34)3)(1()(2-+-=---=x x x x x f .（2）3sin 4)(sin )(sin 2-+-==x x x f y ，1)2(sin 2+--=∴x y]1,0[sin ],2,0[∈∴∈x x π，当0sin =x 时，3min -=y ；当1sin =x ，0max =y .17.解：由,55cos )2sin(-==+x απ，又),0(πα∈，552sin =∴x ，2tan -=∴x .（1）原式=31tan 1tan 1sin cos sin cos cos sin sin cos -=-+==+=---xx xx x x xx x x ；（2）原=)sin cos cos sin 2(222cos 222sin 2222αααααα-+=+=1027tan 1tan 1tan 222cos sin sin cos cos sin 222222222-=+-+⋅=+-+⋅ααααααααα18.解：当P 命题为真命题时，10<<a ；∴当P 命题为假命题时，0≤a 或1≥a .当Q 命题为真命题时，即不等式04)2(2)2(2<--+-x a x a 对任意实数x 恒成立, ①当02=-a 即2=a 时，04<-对任意实数x 恒成立；②当02≠-a 即2≠a 时，⎩⎨⎧<-+-=∆<-0)2(16)2(4022a a a 即22<<-a . 由①②知，22≤<-a ,∴Q 为假命题时，2-≤a 或2>a . 又P 或Q 为假命题时，则P ，Q 都为假命题，此时a 的取值范围为：2-≤a 或2>a .从而P 或Q 为真命题时，a 的取值范围为：22≤<-a . 19.解：22cos 12sin 21sin cos sin )(2xx x x x b a x f -+=+=⋅==21)42(sin 22+-πx（1）)(x f 的最小正周期为π； （2）当]2,0[π∈x 时，]43,4[42πππ-∈-x ，∴当242ππ=-x ，即83π=x 时，)(x f 有最大值212+；（3）当],0[π∈x 时，]47,4[42πππ-∈-x ，由x y sin =的图像知，]23,2[42πππ∈-x ，即]87,83[ππ∈x 时，)(x f 单调递减，∴)(x f 的单调递减区间为]87,83ππ.20.解：（1）223)(2'++=bx ax x f ，又)(x f 在2,1=-=x x 处取得极值，⎪⎩⎪⎨⎧==-∴0)2(0)1(''f f 即⎪⎪⎩⎪⎪⎨⎧=-=⇒⎩⎨⎧=++=+-2131024120223b a b a b a ； （2）方程023322)(2323=++-=+--+t x x x t x x x x f 在区间]2,21[上恰有两个不相等的实数根，即方程t x x x -=+-232332在区间]2,21[上恰有两个不相等的实根，令=)(x g x x x +-232332，]2,21[∈x ，则=)('x g 1322+-x x ， 令0)('=x g 解得21=x 或1=x ；当x 变化时，)(),('x g x g 的变化列表如下：x21)1,21( 1)2,1(2)('x g- 0 +)(x g 245↓ 极小值61↑34要使t x g -=)(在]2,21[∈x 上有两个不相等实根，则应满足24561≤-<t ，即t 的取值范围为)61,245[--.21.解：（1）2=m 时，x x x x f 3231)(23+-=，34)(2'+-=x x x f ，函数在)0,0(处切线的斜率为3)0('=f ，∴在)0,0(处切线方程为：03=-y x .（2）函数)(x f 的定义域为R ，m mx x x f 232)(2'+-=，方程02322=+-m mx x 的判别式m m 642-=∆，①当0642≤-=∆m m ，即230≤<m 时，0)('≥x f 对一切实数恒成立，)(x f ∴在),(+∞-∞上单调递增；②当0642>-=∆m m ，即23>m 时，方程02322=+-m mx x 有两不等实根，m m m x 2321--=，m m m x 2322-+=，当),(1x x -∞∈及),(2+∞x 时，0)('>x f ，)(x f ∴单调递增； 当),(21x x x ∈时，0)('<x f ，)(x f ∴单调递减. 综上所述，当230≤<m 时，)(x f 在),(+∞-∞上单调递增；当23>m 时，)(x f 在)23,(2m m m ---∞及),23(2+∞-+m m m 上单调递增，在,23(2m m m --)232m m m -+上单调递减.（3）由（2）知方程0232)(2'=+-=m mx x x f 有两不等根，0642>-=∆m m ，即23>m ,令=)(x g =----332)323()(22x m m mx x f 3323231223-+-x m mx x ，要使332)323()(22+-+≤x m m mx x f 对m x 40≤≤的实数恒成立，只需0)(max ≤x g 即可，下面求)(x g 在]4,0[m x ∈上的最大值，0)2)(()(,34)('22'=--=+-=m x m x x g m mx x x g 令 ，则m x m x 2,==，33234)(3-=m m g ，332)3(-=m g ，又,332)0(-=g 33234)4(3-=m m g ，∴当]4,0[m x ∈时，33234)(3max -=m x g ，∴0332343≤-m ，即2≤m ，又23>m ，m ∴的取值范围为]2,23(.。

2013年陕西省西安市某校高考数学三模试卷（文科）一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的（本大题共10小题，每小题5分，共50分） 1. 复数z =i 1+i在复平面上对应的点位于( )A 第一象限B 第二象限C 第三象限D 第四象限2. 若a ，b ，c ，d ∈R ，且a >b ，c >d ，则下列结论正确的是（ ） A ac 2>bc 2 B ac >bd C 1a <1b D a +c >b +d3. 设函数f(x)=x 2−x −2，x ∈[−5, 5]．若从区间[−5, 5]内随机选取一个实数x 0，则所选取的实数x 0满足f(x 0)≤0的概率为（ ） A 0.5 B 0.4 C 0.3 D 0.24. 如果等差数列{a n }中，a 3+a 4+a 5＝12，那么a 1+a 2+...+a 7＝（ ） A 14 B 21 C 28 D 355. 已知某几何体的三视图如图所示，则此几何体的体积是（ ）A 12 B 14 C 16 D 186. 已知m ，n 是两条不同直线，α，β，γ是三个不同平面，下列命题中正确( )A 若m // α，n // α，则m // nB 若α⊥γ，β⊥γ，则α // βC 若m ⊥α，n ⊥α，则m // nD 若m // α，m // β，则α // β7. 过点P(4, 2)作圆x 2+y 2=4的两条切线，切点分别A ，B ，O 是坐标原点，则△AOB 外接圆的方程为（ ）A (x −4)2+(y −2)2=20B (x −2)2+(y −1)2=5C (x +4)2+(y +2)2=20D (x +2)2+(y +1)2=5 8. 已知F 1、F 2分别为椭圆x 216+y 29=1的左、右焦点，椭圆的弦DE 过焦点F 1，若直线DE 的倾斜角为α(α≠0)，则△DEF 2的周长为（ ） A 64 B 20 C 16 D 随α变化而变化9. 已知函数y =sin(π4−2x)，则其图象的下列结论中，正确的是（ ）A 关于点(−π8，1)中心对称B 关于直线x =π8轴对称C 向左平移π8后得到奇函数 D 向左平移π8后得到偶函数10. f(x)是定义在R 上的奇函数，当x >0时，(x 2+1)f′(x)+2xf(x)<0，且f(−1)=0，则不等式f(x)>0的解集是（ ）A (1, +∞)B (−1, 0)∪(1, +∞)C (−∞, −1)D (−∞, −1)∪(0, 1)二、填空题：本大题共5小题，每小题5分，共25分．将答案填写在题中的横线上．11. 集合A={−1, 0, 1}，B={x|x=m2+1, m∈R}，则A∩B=________．12. 阅读如图的程序框图，若输入m=4，n=6，则输出的a等于________．13. 当x，y满足{|x−1|≤1y≥0y≤x+1时，则t=x−2y的最小值是________．14. 观察下列不等式：1+122<32，1+122+132<53，1+122+132+142<74，…由以上不等式推测到一个一般的结论：对于n∈N∗，1+122+132+⋯+1n2<________．15. （考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分）A．（选修4−5不等式选讲）若任意实数x使m≥|x+2|−|5−x|恒成立，则实数m的取值范围是________；B．（选修4−1几何证明选讲）如图：EB、EC是⊙O的两条切线，B、C是切点，A、D是⊙O上两点，如果∠E=46∘，∠DCF=32∘，则∠A的度数是________；C．（选修4−4坐标系与参数方程）极坐标系下，直线ρcos(θ−π4)=√2与圆ρ=√2的公共点个数是________．三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．16. 已知△ABC的角A、B、C所对的边分别是a、b、c，设向量m→=(a,b)，n→=(sinB,sinA)，p→=(b−2,a−2)．（1）若m→ // n→，求证：△ABC为等腰三角形；（2）若m→⊥p→，边长c＝2，角C=π，求△ABC的面积．317. 设数列{a n}的前n项和为S n，且S n=2a n−3(n=1, 2,…)．（1）证明：数列{a n}是等比数列；（2）若数列{b n}满足b n=a n+2n(n=1, 2,…)，求数列{b n}的前n项和为T n．18. 如图，在四棱锥P−ABCD中，底面ABCD为菱形，其中PA=PD=AD=2，∠BAD=60∘，Q为AD的中点．（1）求证：AD⊥平面PQB；PC，求四棱锥M−ABCD的体积．（2）若平面PAD⊥平面ABCD，且PM=1219. 某企业员工500人参加“学雷锋”志愿活动，按年龄分组：第1组[25, 30)，第2组[30, 35)，第3组[35, 40)，第4组[40, 45)，第5组[45, 50]，得到的频率分布直方图如图所示．(Ⅰ)下表是年龄的频数分布表，求正整数a，b的值；的人数分别是多少？(Ⅲ)在(Ⅱ)的前提下，从这6人中随机抽取2人参加社区宣传交流活动，求至少有1人年龄在第3组的概率．20. 在平面直角坐标系中，已知曲线C上任意一点P到两个定点F1(−√3,0)和F2(√3,0)的距离之和为4．（1）求曲线C的方程；（2）设过(0, −2)的直线l与曲线C交于A、B两点，以线段AB为直径作圆．试问：该圆能否经过坐标原点？若能，请写出此时直线l的方程，并证明你的结论；若不是，请说明理由．21. 设函数f(x)=x2−mlnx，ℎ(x)=x2−x+a．（1）若曲线y=f(x)在x=1处的切线为y=x，求实数m的值；（2）当m=2时，若方程f(x)−ℎ(x)=0在[1, 3]上恰好有两个不同的实数解，求实数a的取值范围；（3）是否存在实数m，使函数f(x)和函数ℎ(x)在公共定义域上具有相同的单调性？若存在，求出m的值，若不存在，说明理由．2013年陕西省西安市某校高考数学三模试卷（文科）答案1. A2. D3. C4. C5. C6. D7. B8. C9. C10. D11. {1}12. 1213. −414. 2n−1n15. [7, +∞),99∘,116. ∵ m // n∴ asinA＝bsinB即a⋅a2R =b⋅b2R．其中R为△ABC外接圆半径．∴ a＝b∴ △ABC为等腰三角形．由题意，m⋅p＝0∴ a(b−2)+b(a−2)＝0∴ a+b＝ab由余弦定理4＝a2+b2−2ab⋅cosπ3∴ 4＝a2+b2−ab＝(a+b)2−3ab ∴ (ab)2−3ab−4＝0∴ ab＝4或ab＝−1（舍去）∴ S△ABC=12absinC=12×4×sinπ3=√317. （1）证明：因为S n=2a n−3(n=1, 2,…)．，则S n−1=2a n−1−3(n=2, 3,…)．…所以当n≥2时，a n=S n−S n−1=2a n−2a n−1，…整理得a n=2a n−1．…由S n=2a n−3，令n=1，得S1=2a1−3，解得a1=3．…所以{a n}是首项为3，公比为2的等比数列．…（2）解：因为a n=3⋅2n−1，…由b n=a n+2n(n=1, 2,…)，得b n=3⋅2n−1+2n．所以T n=3(1+21+22+⋯+2n−1)+2(1+2+3+⋯+n)…=31(1−2n)1−2+2⋅n(n+1)2…=3⋅2n+n2+n−3所以T n=3⋅2n+n2+n−3．…18. 解：（1）连接BD∵ PA=PD=AD=2，Q为AD的中点，∴ PQ⊥AD又∵ ∠BAD=60∘，底面ABCD为菱形，∴ △ABD是等边三角形，∵ Q为AD的中点，∴ AD⊥BQ∵ PQ、BQ是平面PQB内的相交直线，∴ AD⊥平面PQB．（2）连接QC，作MH⊥QC于H．∵ 平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，PQ⊥AD∴ PQ⊥平面ABCD，结合QC⊂平面ABCD，可得PQ⊥QC∵ 平面PQC中，MH⊥QC且PQ⊥QC，∴ PQ // MH，可得MH⊥平面ABCD，即MH就是四棱锥M−ABCD的高线∵ PM=12PC，可得MH=12PQ=12×√32×2=√32，∴ 四棱锥M−ABCD的体积为V M−ABCD=13×12AC×BD×MH=16×2×2√3×√32=1．19. （1）由题设可知，a＝0.08×5×500＝200，b＝0.02×5×500＝50．（2）因为第1，2，3组共有50+50+200＝300人，利用分层抽样在300名学生中抽取6名学生，每组抽取的人数分别为：第1组的人数为6×50300=1，第2组的人数为6×50300=1，第3组的人数为6×200300=4，所以第1，2，3组分别抽取1人，1人，4人．(Ⅲ)设第1组的1位同学为A，第2组的1位同学为B，第3组的4位同学为C1，C2，C3，C4，则从六位同学中抽两位同学有：(A, B)，(A, C1)，(A, C2)，(A, C3)，(A, C4)，(B, C1)，(B, C2)，(B, C3)，(B, C4)，(C1, C2)，(C1, C3)，(C1, C4)，(C2, C3)，(C2, C4)，(C3, C4)，共15种可能．其中2人年龄都不在第3组的有：(A, B)，共1种可能，所以至少有1人年龄在第3组的概率为1−115=1415．20. 解：（1）根据椭圆的定义，可知动点P的轨迹为椭圆，其中a =2，c =√3，则b =√a 2−c 2=1． 所以动点P 的轨迹方程为x 24+y 2=1．（2）当直线l 的斜率不存在时，不满足题意．当直线l 的斜率存在时，设直线l 的方程为y =kx −2，设A(x 1, y 1)，B(x 2, y 2)， 若OA →⋅OB →=0，则x 1x 2+y 1y 2=0．∵ y 1=kx 1−2，y 2=kx 2−2，∴ y 1y 2=k 2x 1⋅x 2−2k(x 1+x 2)+4． ∴ (1+k 2)x 1x 2−2k(x 1+x 2)+4=0．…①由方程组{x 24+y 2=1y =kx −2得(1+4k 2)x 2−16kx +12=0．∵ △=162k 2−4×12×(1+4k 2)>0，∴ k 2>34…②则x 1+x 2=16k1+4k 2，x 1⋅x 2=121+4k 2，代入①，得(1+k 2)121+4k 2−2k 16k1+4k 2+4=0．即k 2=4，解得k =2或k =−2，满足②式．因此存在直线l ，其方程为y =2x −2或y =−2x −2． 21. 解：（1）∵ 函数f(x)=x 2−mlnx ， ∴ 切点为(1, 1)，f′(x)=2x −mx ，∵ 曲线y =f(x)在x =1处的切线为y =x ， ∴ k =f ′(1)=1，即m =1（2）f(x)−ℎ(x)=0，等价于x 2−2lnx =x 2−x +a ，即a =x −2lnx 令g(x)=x −2lnx ，则g ′(x)=1−2x =x−22∴ x ∈[1, 2]时，g′(x)≤0，函数g(x)=x −2lnx 在[1, 2]内单调递减；x ∈[2, 3]时，g′(x)≥0，函数g(x)=x −2lnx 在[2, 3]内单调递增． 又因为g(1)=1，g(2)=2−2ln2，g(3)=3−2ln3 故2−2ln2<a ≤3−2ln3（3）∵ ℎ(x)=x 2−x +a 在(0,12)单调递减；(12，+∞)单调递增 ∴ f(x)=x 2−mlnx 也应在(0,12)单调递减；(12，+∞)单调递增 ∵ f ′(x)=2x −m x=2x 2−m x，∴ 当m ≤0时，f(x)=x 2−mlnx 在(0, +∞)单调递增，不满足条件；当m >0且√m2=12，即m =12，函数f(x)和函数ℎ(x)在公共定义域上具有相同的单调区间．。

陕西省宝鸡市南山高级中学2023-2024学年高一上学期第二次月考数学试题一、单选题1．已知命题:0p x ∀>，25410x x -+≥，则命题p 的否定为（ ）A ．0x ∀>，25410x x -+<B ．0x ∀<，25410x x -+<C ．0x ∃>，25410x x -+<D ．0x ∃<，25410x x -+< 2．把390︒化成弧度为（ ）A ．53πB ．94πC ．73πD ．136π 3．已知集合{}{}213,A x x B x x a =-<=>，若B A ⊆R ð，则实数a 的取值范围为（ ） A ．(),2-∞- B ．(],2-∞ C ．[)2,+∞ D ．()2,+∞ 4．函数1()ln(2)f x x x =-+的定义域是（ ） A ．(],2-∞B ．()0,2C ．()(),00,2-∞UD ．()(],00,2-∞⋃5．设 3.131ln 3,log ,0.22a b c ===，则,,a b c 的大小关系为（ ） A ．c b a <<B ．b a c <<C ．a b c <<D ．b<c<a 6．函数()21ln f x x x =-的零点所在的区间是（ ） A ．()0,1 B ．()2,3 C ．()1,2 D ．()3,5 7．已知关于x 的不等式0mx n ->的解集为{}2x x <-，函数2()(1)x f x b a =+（0a >且0a ≠）为指数函数，则()()2f n f m ⋅=⎡⎤⎣⎦（ ）A ．1B ．2C ．3D ．4 8．若定义在R 上的偶函数()f x 在区间[)0,∞+上单调递增，且()30f =，则满足()()20f x f x -≤的x 的取值范围为（ ）A ．(](]3,13,5--UB ．()()3,13,5--UC ．(][),15,-∞-⋃+∞D ．[][)3,15,--+∞U二、多选题9．关于x 的不等式220x mx ++>对任意x ∈R 恒成立的充分不必要条件有（ ） A ．02m ≤≤ B．1m -≤≤C ．12m -≤≤ D．m -<10．下列命题为真命题的是（ ）A ．若a b >，则22ac bc >B ．若32a -<<，14b <<，则71a b -<-<C ．若0b a <<，0m <，则m m a b> D ．若0a b >>，0c d >>，则ac bd >11．若α是第二象限角，则（ ）A ．πα-是第一象限角B ．2α是第一或第三象限角 C ．32πα+是第二象限角 D ．2α是第三或第四象限角12．已知函数2()23f x x x =--，()3g x x =-，对x ∀∈R ，()f x 与()g x 中的最大值记为()()(){}max ,m x f x g x =，则（ ）A ．函数()f x 的零点为()1,0-，()3,0B ．函数()m x 的最小值为3-C ．方程()3m x =有3个解D ．方程()()f f x m =最多有4个解三、填空题13．桃湖公园有一扇形花园，扇形的圆心角为120o ，半径为30m ，现要在该花园的周围围一圈护栏，则护栏的总长度为（结果保留π）m ．14．已知(31)4,1()log ,1aa x a x f x x x -+<⎧=⎨≥⎩是(,)-∞+∞上的减函数，那么a 的取值范围是. 15．已知关于x 的方程()22140x m x m -++=的两根分别在区间()01，，()12，内，则实数m 的取值范围为．16．已知函数()22,0,log ,0,x x f x x x ⎧≤⎪=⎨>⎪⎩则使()()0f f x =的x 组成的集合为.四、解答题17．设集合A ＝{x |x 是小于9的正整数}，集合B ＝{1，2，3}，集合C ＝{3，4，5，6}．求：A ∩C ，A ∩（B ∪C ），A ∪（B ∩C ）．18．（1）若23x =，求42x x -+的值；（2）求值：322425lg 22lg 2lg5lg 516log 5log 16+⋅+++⋅. 19．已知幂函数()f x 与一次函数()g x 的图象都经过点()4,2，且()()95f g =.(1)求()f x 与()g x 的解析式；(2)求函数()()()h x g x f x =-在[]0,1上的值域.20．已知函数()()212log 23f x x ax =-+ (1)若()f x 的值域为R ，求实数a 的取值范围；(2)若()f x 在[]1,2内为单调函数，求实数a 的取值范围.21．国庆黄金周期间，旅游潮、探亲潮必将形成高交通压力现象.已知某火车站候车厅，候车人数与时间t 相关，时间(t 单位：小时)满足024t <…，N.t ∈经测算，当1624t ≤≤时，候车人数为候车厅满厅状态，满厅人数为5000人，当016t <<，候车人数相对于满厅人数会减少，减少人数与()16t t -成正比，且时间为6点时，候车人数为3800人，记候车厅候车人数为()f t ．(1)求()f t 的表达式，并求当天中午11点时，候车厅候车人数;(2)铁路系统为了体现“人性化”管理，每整点时会给旅客提供的免费面包数量为()3000400f t P t -=+，则当t 为何值时需要提供的免费面包数量最少.22．定义在()2,2-上的函数()f x 满足对任意的(),2,2x y ∈-，都有()()()f x f y f x y +=+，且当()0,2x ∈时，()0f x >．(1)证明：函数()f x 是奇函数；(2)证明：()f x 在()2,2-上是增函数；(3)若()12f -=-，()21f x t at ≤+-对任意[]1,1x ∈-，[]2,2a ∈-恒成立，求实数t 的取值范围．。