中考数学《第21课时：三角形的基础知识》同步练习(含答案)

人教版九年级上册数学第二十一章练习和习题答案人教版九年级上册数学第4页练习答案1.解：（1）5x²-4x-1=0，二次相系数为5，一次项系数为-4，常数项为-1.（2）4x²-81=0，二次项系数为4，一次项系数为0，常数项为-81. （3）4x²+8x-25=0，二次项系数为4，一次项系数为8，常数项为-25.（4）3x²-7x+1=0，二次项系数为3，一次项系数为-7，常数项为1.【规律方式：化为一般形式即把所有的项都移到方程的左侧，右边化为0的行驶，在肯定二次项系数，一次项系数和常数项时，要特别注意各项系数及常数项均包括前面的符号.】2.解：（1）4x²=25，4x²-25=0.（2）x（x-2）=100，x²-2x-100=0.（3）x∙1=（1-x）²-3x+1=0.人教版九年级上册数学第6页练习答案解：（1）2x²-8=0，∴x²=4，∴x_1=2，x_2=-2.（2）9x^2-5=3，移项，得9x^2=8，x^2=8/9，∴x_1=(2√2)/3，x_2=-(2√2)/3.（3）（x+6）²-9=0，移项，得（x+6）²=9.∴x+6=±3，∴x_1=-3，x_3=-9.（4）3（x-1）²-6=0，移项，化简得（x-1）²=2，∴x-1=±√2，∴x_1=1-√2，x_2=1+√2.（5）x²-4x+4=5，（x-2）²=5，∴x-2=±√5，∴x_1=2-√5，x_2=2+√5.（6）9x²+5=1.9x²=1-5，9x^2=-4.∵-4<0，,9x^2+5=1-5,9x^2=-4.∵-4<0，,9x^2+5=1无实数根.【规律方式：利用直接开平方式，首先应把方程化为左侧是含未知数的完全平方的形式.】人教版九年级上册数学第9页练习答案1.（1）25 5 （2）36 6 （3）25/4 5/2 （4）1/9 1/3【规律方式：对一个式子进行配方，先将二次项的系数变成1，然后在一次项以后加上一次项系数一般的平方，即得完全平方式.】2.解：（1）x²+10x+9=0，x²+10x+25-25+9=0，（x+5）²=16，x+5=±4，∴x_1=-1，x_2=-9.（2） x^2-x-7/4=0，x^2-x+（1/2）^2-（1/2）²-7/4=0，（x-1/2）²=2，x-1/2=±√2，∴x_1=1/2-√2，x_2=1/2+√2.（3）3x²+6x-4=0,3（x²+2x）-4=0.3（x²+2x+1-1）-4=0.3（x+1）²=7，（x+1）²=7/3，x+1=±√21/3，x_1=-1-√21/3，x_2=-1+√21/3.（4）4x^2-6x-3=0,4（x^2-3/2 x）=3，（x-3/4）^2=21/16，x-3/4=±√21/4，∴x_1=3/4-√21/4,x_2=3/4+√21/4.（5）x²+4x-9=2x-11，x²+2x+2=0，（x+1）²=-1，∴原方程无实数根.（6）x（x+4）=8x+12，x²-4x-12=0，（x-2）²=16，x-2=±4，∴x_1=6，x_2=-2.【规律方式：配方式解方程时，补充的项应为一次项系数一半的平方，组成完全平方后，在用直接开平方式来解.】人教版九年级上册数学第12页练习答案1.解：（1）x²+x-6=0，∵a=1，b=1，c=-6，∴b²-4ab=1+24=25>0，∴x=(-1±√25)/2，∴x_1=(-1-5)/1=-3，x_2=(-1+5)/2=2. （2） x^2-√3 x- 1/4=0，∵a=1，b=-√(3,)c=-1/4，∴b²-4ac=3-4×（-1/4）=4>0，∴x= (√3±2)/2，∴x_1=(√3-2)/2，x_2=(√3+2)/2.（3）3x²-6x-2=0，∵a=3，b=-6，c=-2，∴b²-4ac=36-4×3×（-2）=60>0，∴x= (6±√60)/(2×3)=(6±2√15)/6=(3±√15)/3，∴x_1=(3-√15)/3，x_2=(3+√15)/3.（4）4x²-6x=0，∵a=4，b=-6，c=0，∴b²-4ac=36-4×4×0=36>0，∴x= (6±6)/(2×4)，x_1=0，x_2=3/2.（5）x²+4x+8=4x+11，整理，得x²-3=0，∵a=1，b=0，c=-3，∴b²-4ac=0-4×1×（-3）=12>0，∴x= (±√12)/2=±√3，∴x_1=√3，x_2=-√3.（6）x（2x-4）=5-8x，整理，得2x²+4x-5=0，∵a=2，b=4，c=-5，∴b²-4ac=16-4×2×（-5）=56，∴=(-4+√56)/(2×2)=(-4±2√14)/4=(-2±√14)/2，∴x_1=(-2-√14)/2，x_2=(-2+√14)/2.【规律方式：利用公式法解方程有如下四个步骤：一是将方程化为一般形式，即ax²+bx+c=0（a≠0）的形式；二是找出二次项系数a，一次项系数b及常数项c；三是求出b²-4ac的值；四是将a，b，b²-4ac的值代入求根公式，求出方程解.】2.解：x²-75x+350=0，∵a=1，b=-75，c=350，∴b²-4ac=（-75）²-4×1×350=4225，∴x= (75±√4225)/(2×1)=(75±65)/2，∴x_1=5，x_2=70（舍去）.答：应切去边长为5cm的正方形.人教版九年级上册数学第14页练习答案1.解：（1）x²+x=0，x（x+1）=0，∴x=0或x+1=0，∴x_1=0,x_2=-1.（2）x²-2√3 x=0，x（x-2√3）=0，∴=0或x-2√3=0，∴x_1=0，x_2=2√3.（3）3x²-6x=-3，x²-2x+1=0，（x-1）²=0，∴x_1=x_2=1.（4）4x²-121=0，（2x-11）∙（2x+11）=0，∴2x-11=0或2x+11=0，∴x_1=11/2，x_2=-11/2.（5）3x（2x+1）=4x+2,3x（2x+1）-2（2x+1）=0，（2x+1）（3x-2）=0，,2x+1=0或3x-2=0，∴x_1=-1/2，x_2=2/3.（6）（x-4）²=（5-2x）²，（x-4）²-（5-2x）²=0，（x-4+5-2x）（x-4-5+2x）=0，（1-x）（3x-9）=0，∴1-x=0或3x-9=0，∴x_1=1，x_2=3.2.解：设小圆形场地的半径为Rm，则大圆形场地的半径为（R+5）m，由题意，得2πR²=π（R+5）^2，2R²=（R+5）^2，R²-10R-25=0，∴R= (10±√(10²+4×25))/2=(10±10√2)/2=5±5√2，R1=5-5√2（舍去），R2=5+5√2.答：小圆形场地的半径为（5+5√2）m.人教版九年级上册数学第16页练习答案解：（1）设x_1，x_2是方程x²-3x=15的两根，整理x²-3x=15，x²-3x-15=0，所以x_1+x_2=3，x_1∙x_2=-15.（2）设x_1，x_2 是方程3x²+2=1-4x的两根，整理3x²+2=1-4x，得3x²+4x+1=0，所以x_1+x_2=-4/3，x_1∙x_2=1/3.（3）设x_1，x_2 是方程5x^2-1=4x^2+x的两根，整理5x^2-1=4x^2+x，得x^2-x-1=0，所以x_1+x_2=1，x_1∙x_2=-1.（4）设x_1 x_2是方程2x²-x+2=3x+1的两根，整理方程2x²-x+2=3x+1，得2x²-4x+1=0，所以x_1+x_2=2，x_1 x_2=1/2.人教版九年级上册数学习题21.1答案1.解：（1）3x²-6x+1=0，二次项系数为3，一次项系数-6，常数项为1.（2）4x²+5x-81=0，二次项系数为4，一次项系数为5，常数项为-81.（3）x²+5x=0，二次项系数为1，一次项系数为5，常数项为0.（4）x²-2x+1=0，二次项系数为1，一次项系数为-2，常数项为1.（5）x²+10=0，二次项系数为1，一次项系数为0，常数项为10.（6）x²+2x-2=0，二次项系数为1，一次项系数为2，常数项为-2.2.解：（1）设这个圆的半径为Rm，由圆的面积公式得πR²=6.28，∴πR²-6.28=0.（2）设这个直角三角形较长的直角边长为x cm，由直角三角形的面积公式，得1/2x（x-3）=9，∴x²-3x-18=0.3.解：方程x²+x-12=0的根是-4,3.4.解：设矩形的宽为x cm，则矩形的长为（x+1）cm，由矩形的面积公式，得x ∙（x+1）=132，∴x^2+x-132=0.5.解：设矩形的长为x m，则矩形的宽为（0.5-x）m，由矩形的面积公式，得∙（0.5-x）=0.06，∴x²-0.5x+0.06=0.6.解：设有n人参加聚会，按照题意，可知（n-1）+（n-2）+（n-3）+…+3+2+1=10.即(n(n-1))/2=10,n²-n-20=0.7.解：由题意可知2²-c=0，∴c=4，∴原方程为x²-4=0，∴=±2，∴这个方程的另一个根为-2.人教版九年级上册数学习题21.2答案1.解：（1）36x²-1=0，移项，得36x²=1，直接开平方，得6x=±1，,6x=1或6x=-1，∴原方程的解是x_1=1/6，x_2=-1/6.（2）4x²=81，直接开平方，得2=±9，,2x=9或2x=-9，∴原方程的解是x_1=9/2，x_2=-9/2.（3）（x+5）²=25，直接开平方，得x+5=±5，∴+5=5或x+5=-5，∴原方程的解是x_1=0，x_2=-10.（4）x²+2x+1=4，原方程化为（x+1）^2=4，直接开平方，得x+1=±2，∴x+1=2或x+1=-2，∴原方程的解是x_1=1，x_2=-3.2.（1）9 3 （2）1/4 1/2 （3）1 1 （4）1/25 1/53.解：（1）x²+10x+16=0，移项，得x²+10x=-16，配方，得x²+10x+5²=-16+5²，即（x+5）²=9，开平方，得x+5=±3，∴+5=3或x+5=-3，∴原方程的解为x_1=-2，x_2=-8.（2）x²-x-3/4=0，移项，得x^2-x=3/4，配方，得x^2-x=3/4，配方，得x^2-x+1/4=3/4+1/4，即（x-1/2）^2=1，开平方，得x- 1/2=±1，∴原方程的解为x_1=3/2，x_2=-1/2.（3）3x²+6x-5=0,二次项系数化为1，得x²+2x-5/3=0，移项，得x²+2x=5/3，配方，得x²+2x+1=5/3+1，即（x+1）²=8/3，开平方，得x+1=±2/3 √6，∴x+1=2/3 √6或x+1=-2/3 √6，∴原方程的解为x_1=-1+2/3 √6，x_2=-1-2/3 √6. （4）4x²-x-9=0，二次项系数化为1，得x²-1/4x-9/4=0，移项，得x²-1/4 x= 9/4，配方，得x²-1/4x+1/64=9/4+1/64，即（x-1/8）²=145/64，开平方，得x-1/8=±√145/8，∴x-1/8=√145/8 或x- 1/8=-√145/8，∴原方程的解为x_1=1/8+√145/8，x_2=1/8-√145/8.4.解：（1）因为△=（-3）²-4×2×（-3/2）=21>0，所以原方程有两个不相等的实数根.（2）因为△=（-24）²-4×16×9=0，所以与原方程有两个相等的实数根.（3）因为△=（-4√2）^2-4×1×9=-4<0，因为△=（-8）²-4×10=24>0，所以原方程有两个不相等的实数根.5.解：（1）x²+x-12=0，∵a=1，b=1，c=-12，∴b²-4ac=1-4×1×（-12）=49>0，∴x= (-1±√49)/2=(-1±7)/2，∴原方程的根为x_1=-4，x_2=3.（2）x²-√2x-1/4=0，∵a=1，b=-√2，c=-1/4，∴b²-4ac=2-4×1×（-1/4）=3>0，∴x= (√2+√3)/2，∴原方程的根为x_1=(√2+√3)/2，x_2=(√2-√3)/2.（3）x²+4x+8=2x+11，原方程化为x²+2x-3=0，∵a=1，b=2，c=-3，∴b²-4ac=2²-4×1×（-3）=16>0，∴x= (-2±√16)/(2×1)=(-2±4)/2，∴原方程的根为x_1=-3，x_2=1.（4）x（x-4）=2-8x，原方程化为x²+4x-2=0，∵a=1，b=4，c=-2，∴b²-4ac=4²-4×1×（-2）=24>0，∴x= (-4±√24)/(2×1)=(-4±2√6)/2，原方程的根为x_1=-2+√6，x_2=-2√6.（5）x²+2x=0，∵a=1，b=2，c=0，∴b²-4ac=2²-4×1×0=4>0，∴x= (-2±√4)/(2×1)=(-2±2)/2，∴原方程的根为x_1=0，x_2=-2. （6）x^2+2√5x+10=0，∵a=1，b=2√5，c=10，∴b^2-4ac=（2√5）²-4×1×10=-20<0，∴原方程无实数根.6.解：（1）3x²-12x=-12，原方程可化为x²-4x+4=0，即（x-2）²=0，∴原方程的根为x_1=x_2=2.（2）4x^2-144=0，原方程可化为4（x+6）（x-6），∴x+6=0或x-6=0，∴原方程的根为x_1=-6，x_2=6.（3）3x（x-1）=2（x-1），原方程可化为（x-1）∙（3x-2）=0，∴x-1=0或3x-2=0，∴原方程的根为x_1=1，x_2=2/3.（4）（2x-1）²=（3-x）²，原方程可化为【（2x-1）+（3-x）】【（2x-1）-（3-x）】=0，即（x+2）（3x-4）=0，∴x+2=0或3x-4=0，∴原方程的根为x_1=-2，x_2=4/3.7.解：设原方程的两根别离为x_1，x_2.（1）原方程可化为x^2-3x-8=0，所以x_1+x_2=3，x_1∙x_2=-8.（2）x_1+x_2=-1/5，x_1∙x_2=-1.（3）原方程可化为x²-4x-6=0，所以x_1+x_2=4，x_1∙x_2=-6.（4）原方程可化为7x²-x-13=0，所以x_1+x_2=1/7，x_1∙x_2=-13/7.8.解：设这个直角三角形的较短直角边长为 x cm，则较长直角边长为（x+5）cm，按照题意，得1/2 x（x+5）=7，所以x²+5x-14=0，解得x_1=-7，x_2=2，因为直角三角形的边长为√(x²+（x+5）^2 )=√(2²+7²)=√53 （cm）.答：这个直角三角形斜边的长为√53cm.9.解：设共有x家公司参加商品交易会，由题意可知（x-1）+（x-2）+（x-3）+…+3+2+1=45，即x（x-1）/2=45，∴x^2-x-90=0，即（x-10）（x+9）=0，∴x-10=0或x+9=0，∴x_1=10，x_2=-9，∵x必需是正整数，∴x=-9不符合题意。

初三数学上册第21章全套同步测试题与答案上册第21章全套同步测试题与答案如下1、化简| -2|+ 的结果是( )A.4-2B.0C.2D.42、下列各式中，一定能成立的是( )A. B.C. D.3、已知x4、若，则_________;若，则________.5、当时，求|2- |的值是多少?◆典例分析有一道练习题是：对于式子先化简，后求值.其中.小明的解法如下：= = = = .小明的解法对吗?如果不对，请改正. 分析：本题中有一个隐含条件，即，并由此应将化简为.对这个隐含条件的敏感度是正确解决问题的关键.解：小明的解法对不对.改正如下：由题意得，，应有.◆课下作业●拓展提高1、当-11时，化简得( )A.2B.-2C.2D.-22、计算=_______.3、观察下列各式：请你将发现的规律用含自然数n(n1)的等式表示出来.4、把下列非负数写成一个数的平方的形式:(1)5 (2)3.4 (3) (4)x(x0)5、在实数范围内分解下列因式:(1) (2) (3)6、已知实数满足，求的值是多少?●体验中考1、(2009年，长沙)已知实数在数轴上的位置如图所示,则化简的结果为( )A.1B.-1C.D.(注意：由图可知，我们可以直接利用这个结论解题.) 2、(2019年，广州)实数在数轴上的位置如图所示,化简. (提示：由图可知，可以选择利用和解题.)参考答案：◆随堂检测1、A. ∵有意义，，原式= ，故选A.2、A. ∵只有A选项不含代数字母，等式总成立.故选A.3、0. ∵x4、，∵当时，由得;当时，由得，即.5、解：当时，, ,|2- |=|2- |=| |= .◆课下作业●拓展提高1、A. ∵当-11时，，故选A.2、可以直接利用( )的结论解题. = .3、= .4、解：(1)5=( )2 (2)3.4=( )2(3) =( )2 (4)x=( )2(x0).5、解：(1)(2)(3)6、解：∵实数满足，由可得：，化简得：，，.●体验中考“教书先生”恐怕是市井百姓最为熟悉的一种称呼，从最初的门馆、私塾到晚清的学堂，“教书先生”那一行当怎么说也算是让国人景仰甚或敬畏的一种社会职业。

2.1三角形同步检测一、单选题1.小明与小王家相距5km，小王与小邓家相距2km，则小明与小邓家相距（）A.3kmB.7kmC.3km或7kmD.不小于3km也不大于7km2.下列长度的各组线段首尾相接能构成三角形的是（）A.3cm、5cm、8cmB.3cm、5cm、6cmC.3cm、3cm、6cmD.3cm、5cm、10cm3.△ABC中，∠A=60°，∠C=70°，则∠B的度数是（）A.50°B.60°C.70°D.90°4.图中的五角星是用螺栓将两端打有孔的5根木条连接而构成的，它的形状不稳定．如果用在图中木条交叉点打孔加装螺栓的办法来达到使其形状稳定的目的，且所加螺栓尽可能少，那么需要添加螺栓（）A.1个B.2个C.3个D.4个5.如图，∠ABC=∠ACB，AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF．以下结论：①AD∥BC；②∠ACB=2∠ADB；③∠ADC=90°-∠ABD；④BD平分∠ADC；⑤∠BDC=∠BAC．其中正确的结论有（）A.2个B.3个C.4个D.5个6.下列每组数分别表示三根木棒的长度，将它们首尾连接后，能摆成三角形的一组是()A.1，2，6B.2，2，4C.1，2，3D.2，3，47.三角形的三条高线的交点在三角形的一个顶点上，则此三角形是（）A.直角三角形B.锐角三角形C.钝角三角形D.等腰三角形8.如图，一扇窗户打开后，用窗钩AB可将其固定，这里所运用的几何原理是（）A.三角形的稳定性B.两点之间线段最短C.两点确定一条直线D.垂线段最短9.已知三角形两边的长分别是3和7，则第三边的长可以是（）A.3B.6C.10D.1610.如图，为估计池塘岸边A、B两点的距离，小方在池塘的一侧选取一点O，测得OA=15米，OB=10米，A、B 间的距离不可能是（）A.5米B.10米C.15米D.20米二、填空题11.在△ABC中，∠C=90°，∠A：∠B=1：2，则∠A=________度．12.如图，在△ABC中，点D是BC上一点，∠BAD=80°，AB=AD=DC，则∠C=________度．13.工人师傅砌墙的时候，常在长方形门框上斜定一根木条，他利用的原理是________．14.一个三角形的三个外角之比为5：4：3，则这个三角形内角中最大的角是________度．15.一木工师傅现有两根木条，木条的长分别为40cm和50cm，他要选择第三根木条，将它们钉成一个三角形木架．设第三根木条长为x cm，则x的取值范围是________．16.△ABC中，BD是AC边上的高，∠ABD=70°，∠DBC=40°，则∠ABC=________度．17.如图，在△ABC中，AC=BC，△ABC的外角∠ACE=100°，则∠A=________度．18.如图，由平面上五个点A、B、C、D、E连接而成，则∠A+∠B+∠C+∠D+∠E=________．三、解答题19.已知三角形的一个外角等于60°，且三角形中与这个外角不相邻的两个内角中，其中一个比另一个大10°，则这个三角形的三个内角分别是多少？20.如图，在△ABC中，∠C=∠ABC=2∠A，BD⊥AC于D，求∠DBC的度数．21.已知：如图，直角梯形ABCD中，AD∥BC，∠A=90°，△BCD为等边三角形，且AD=，求梯形ABCD的周长22.如图，已知：AD是△ABC的角平分线，CE是△ABC的高，∠BAC=60°，∠BCE=40°，求∠ADB的度数．23.如图，∠A=90°，∠B=21°，∠C=32°，求∠BDC的度数．参考答案一、单选题1.D2.B3.A4.A5.B6.D7.A8.A9.B10.A二、填空题11.3012.2513.三角形的稳定性14.9015.10cm＜x＜90cm16.110或3017.5018.180°三、解答题19.解：设三角形中与这个外角不相邻的两个内角中较小的为x，则另一个为x+10．x+x+10=60°，解得x=25°．所以三个内角分别是：120°，35°，25°20.解：∵∠C=∠ABC=2∠A，∴∠C+∠ABC+∠A=5∠A=180°，∴∠A=36°．∴∠C=∠ABC=2∠A=72°．∵BD⊥AC，∴∠DBC=90°﹣∠C=18°21.解：∵△BCD是等边三角形，∴∠2=60°，BC=CD=BD，∵AD∥BC，∠A=90°，∴∠ABC+∠A=180°，∴∠ABC=90°，∴∠1=90°﹣60°=30°，在Rt△ABD中，∵∠1=30°，AD=，∴BD=2AD=2，AB=tan30°•AD=，∴梯形ABCD的周长=AD+AB+BC+CD=++2+2=+5．22.解：∵AD是△ABC的角平分线，∠BAC=60°，∴∠DAC=∠BAD=30°，∵CE是△ABC的高，∠BCE=40°，∴∠B=50°，∴∠ADB=180°﹣∠B﹣∠BAD=180°﹣30°﹣50°=100°．23.解：如图，连接AD并延长AD至点E，∵∠BDE=∠BAE+∠B，∠CDE=∠CAD+∠C∴∠BDC=∠BDE+∠CDE=∠CAD+∠C+∠BAD+∠B=∠BAC+∠B+∠C∵∠A=90°，∠B=21°，∠C=32°，∴∠BDC=90°+21°+32°=143°．。

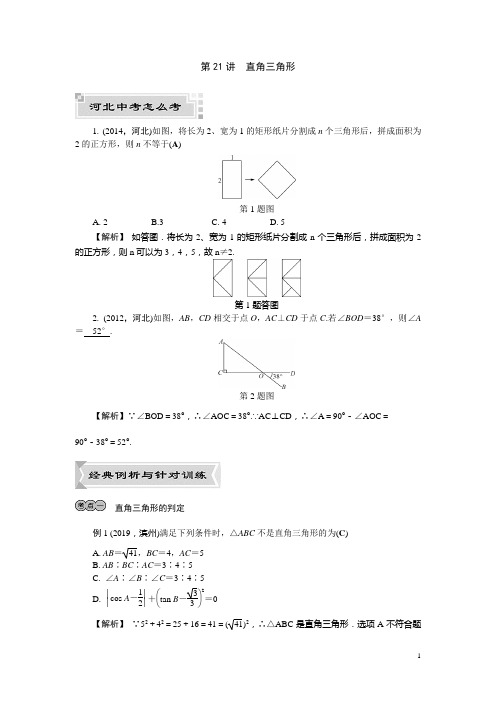
第21讲 直角三角形1. (2014，河北)如图，将长为2、宽为1的矩形纸片分割成n 个三角形后，拼成面积为2的正方形，则n 不等于(A )第1题图A. 2B.3C. 4D. 5【解析】 如答图．将长为2、宽为1的矩形纸片分割成n 个三角形后，拼成面积为2的正方形，则n 可以为3，4，5，故n ≠2.第1题答图2. (2012，河北)如图，AB ，CD 相交于点O ，AC ⊥CD 于点C .若∠BOD ＝38°，则∠A ＝ 52°.第2题图【解析】∵∠BOD ＝38°，∴∠AOC ＝38°.∵AC ⊥CD ，∴∠A ＝90°－∠AOC ＝ 90°－38°＝52°.直角三角形的判定例1 (2019，滨州)满足下列条件时，△ABC 不是直角三角形的为(C ) A. AB ＝41，BC ＝4，AC ＝5 B. AB ∶BC ∶AC ＝3∶4∶5C. ∠A ∶∠B ∶∠C ＝3∶4∶5D. ⎪⎪⎪⎪cos A －12＋⎝⎛⎭⎫tan B －332＝0 【解析】 ∵52＋42＝25＋16＝41＝(41)2，∴△ABC 是直角三角形．选项A 不符合题意．∵(3x)2＋(4x)2＝9x 2＋16x 2＝25x 2＝(5x)2，∴△ABC 是直角三角形．选项B 不符合题意．∵∠A ∶∠B ∶∠C ＝3∶4∶5，∴∠C ＝53＋4＋5×180°＝75°≠90°.∴△ABC 不是直角三角形．选项C 符合题意．∵⎪⎪⎪⎪cos A －12＋⎝⎛⎭⎫tan B －332＝0，∴cos A ＝12，tan B ＝33.∴∠A ＝60°，∠B ＝30°.∴∠C ＝90°.∴△ABC 是直角三角形．选项D 不符合题意．针对训练1 (2019，三明一模)如图，在△ABC 中，CE 平分∠ACB ，CF 平分∠ACD ，且EF ∥BC 交AC 于点M .若CM ＝5，则CE 2＋CF 2＝ 100 .训练1题图【解析】 ∵CE 平分∠ACB ，CF 平分∠ACD ，∴∠ACE ＝12∠ACB ，∠ACF ＝12∠ACD ，即∠ECF ＝12(∠ACB ＋∠ACD)＝90°.∵EF ∥BC ，CE 平分∠ACB ，CF 平分∠ACD ，∴∠ECB＝∠MEC ＝∠ECM ，∠DCF ＝∠CFM ＝∠MCF.∴EM ＝MC ，MF ＝MC.∴EM ＝MF ＝CM ＝5.∴EF ＝10.由勾股定理，可知CE 2＋CF 2＝EF 2＝100.针对训练2一个三角形的周长为38，第一条边长为a ，第二条边长比第一条边长的2倍多3.(1)用含a 的式子表示第三条边长；(2)若这个三角形为等腰三角形，求a 的值；(3)若a 为正整数，则此三角形能否为直角三角形？说明理由． 解：(1)由题意，得第二条边长为2a ＋3. 所以第三条边长为38－a －(2a ＋3)＝35－3a .(2)由三边关系，可知⎩⎪⎨⎪⎧a ＋（2a ＋3）＞35－3a ，a ＋（35－3a ）＞2a ＋3.解得513＜a ＜8.∵a ≠2a ＋3， ∴分两种情况．①a ＝35－3a ，解得a ＝834.不符合三边关系，舍去．②2a ＋3＝35－3a ，解得a ＝625.符合三边关系．∴a ＝625.(3)此三角形不能为直角三角形．理由：∵513＜a ＜8，且a 为正整数，∴a ＝6或7.当a ＝6时，三边长为6，15，17，62＋152≠172，不是直角三角形． 当a ＝7时，三边长为7，17，14，72＋142≠172，不是直角三角形． 综上可知，此三角形不能为直角三角形．直角三角形的性质例2 (2019，安徽模拟)如图，在△ABC 中，∠C ＝90°，AC ＝6，BC ＝8，D 是BC 边的中点，P 是边AB 上的动点．若要使△BPD 为直角三角形，则BP ＝（165或5 ）.例2题图【解析】 在Rt △ABC 中，∵∠C ＝90°，AC ＝6，BC ＝8，∴AB ＝62＋82＝10.∵D 是BC 的中点，∴CD ＝BD ＝4.分两种情形：①当∠DPB ＝90°时，△DPB ∽△ACB ，∴BP BC ＝BDAB.∴BP 8＝410.∴BP ＝165.②当∠PDB ＝90°时，易证DP ∥AC.∵CD ＝DB ，∴AP ＝PB ＝5.综上所述，满足条件的PB 的值为165或5.针对训练3 (2019，上海)如图，已知直线l 1∥l 2，含30°角的三角板的直角顶点C 在l 1上，30°角的顶点A 在l 2上．如果边AB 与l 1的交点D 是AB 的中点，那么∠1＝120°.训练3题图【解析】 如答图．∵D 是斜边AB 的中点，∴DA ＝DC.∴∠DCA ＝∠DAC ＝30°.∴∠2＝∠DCA ＋∠DAC ＝60°.∵l 1∥l 2，∴∠1＋∠2＝180°.∴∠1＝180°－60°＝120°.训练3答图一、选择题1. (2019，深圳福田区模拟)下列性质中，直角三角形具有而等腰三角形不一定具有的是(C)A. 两边之和大于第三边B. 内角和等于180°C. 两个锐角的和等于90°D. 有一个角的平分线垂直于这个角的对边【解析】任意一个三角形两边之和都大于第三边，选项A不符合题意．任意一个三角形的内角和都等于180°，选项B不符合题意．只有直角三角形才有两个锐角的和等于90°，选项C符合题意．等腰三角形顶角的平分线垂直于顶角的对边，而除等腰直角三角形外其他直角三角形没有任何一个角的平分线垂直于这个角的对边，选项D不符合题意．2. 如图，在△ABC中，∠BAC＝90°，AD⊥BC，垂足为D，E是边BC的中点，AD＝ED＝3，则BC的长为(D)第2题图A. 32B. 3 3C. 6D. 62【解析】∵AD＝ED＝3，AD⊥BC，∴△ADE为等腰直角三角形．根据勾股定理，得AE＝32＋32＝3 2.∵在Rt△ABC中，E为BC的中点，∴AE＝12BC.∴BC＝2AE＝6 2.3. (2019，益阳)已知M，N是线段AB上的两点，AM＝MN＝2，NB＝1，以点A为圆心，AN长为半径画弧；再以点B为圆心，BM长为半径画弧，两弧交于点C，连接AC，BC，则△ABC一定是(B)A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等腰三角形【解析】如答图，AC＝AN＝4，BC＝BM＝3，AB＝2＋2＋1＝5，∴AC2＋BC2＝AB2.∴△ABC是直角三角形．第3题答图4. (2019，成都)将等腰直角三角形纸片和矩形纸片按如图方式叠放在一起．若∠1＝30°，则∠2的度数为(B)第4题图A. 10°B. 15°C. 20°D. 30°【解析】 如答图．∵AB ∥CD ，∴∠ADC ＝∠1＝30°.∵△ADE 是等腰直角三角形，∴∠ADE ＝45°.∴∠2＝45°－30°＝15°.第4题答图5. (2019，宁波)已知直线m ∥n ，将一块含45°角的直角三角板ABC 按如图方式放置，其中斜边BC 与直线n 相交于点D .若∠1＝25°，则∠2的度数为(C )第5题图A. 60°B. 65°C. 70°D. 75°【解析】 如答图，设AB 与直线n 相交于点E ，则∠AED ＝∠1＋∠B ＝25°＋45°＝70°.∵直线m ∥n ，∴∠2＝∠AED ＝70°.第5题答图6. (2019，张家口一模)如图，长为8 cm 的橡皮筋放置在x 轴上，固定两端A 和B ，然后把中点C 向上拉升3 cm 至点D ，则橡皮筋被拉长了(A )第6题图A. 2 cmB. 3 cmC. 4 cmD. 5 cm【解析】 ∵C 为AB 的中点，∴AC ＝12AB ＝4 cm ，AD ＝BD.根据题意，得DC ⊥AB ，CD ＝3 cm .在Rt △ACD 中，根据勾股定理，得AD ＝AC 2＋CD 2＝5(cm )．∴AD ＋BD －AB＝2AD －AB ＝10－8＝2(cm )．故橡皮筋被拉长了2 cm .7. (2019，宁波)勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载．如图①，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图②的方式放置在最大的正方形内．若知道图中阴影部分的面积，则一定能求出(C)第7题图A. 直角三角形的面积B. 最大正方形的面积C. 较小两个正方形重叠部分的面积D. 最大正方形与直角三角形的面积和【解析】设直角三角形的斜边长为c，较长直角边长为b，较短直角边长为a.由勾股定理，得c2＝a2＋b2.阴影部分的面积为c2－b2－a(c－b)＝a2－ac＋ab＝a(a＋b－c)，较小两个正方形重叠部分的长为a，宽为a＋b－c，则较小两个正方形重叠部分的面积为a(a＋b－c)．∴知道图中阴影部分的面积，则一定能求出较小两个正方形重叠部分的面积．8. (2019，河南)如图，在四边形ABCD中，AD∥BC，∠D＝90°，AD＝4，BC＝3，分别以点A，C为圆心，大于12AC长为半径作弧，两弧相交于点E，作射线BE交AD于点F，交AC于点O.若O是AC的中点，则CD的长为(A)第8题图A. 2 2B. 4C. 3D. 10【解析】如答图，连接FC，则AF＝FC.∵AD∥BC，∴∠FAO＝∠BCO.∵O是AC的中点，∴OA＝OC.∵∠AOF＝∠COB，∴△FOA≌△BOC(ASA)．∴AF＝BC＝3.∴FC＝AF ＝3，FD＝AD－AF＝4－3＝1.在△FDC中，∵∠D＝90°，∴CD2＋DF2＝FC2.∴CD2＋12＝32.∴CD＝2 2.第8题答图9.(2019，黄石)如图，在△ABC 中，∠B ＝50°，CD ⊥AB 于点D ，∠BCD 和∠BDC 的平分线相交于点E ，F 为边AC 的中点，CD ＝CF ，则∠ACD ＋∠CED 等于(C )第9题图A. 125°B. 145°C. 175°D. 190°【解析】 如答图，连接DF.∵CD ⊥AB ，F 为边AC 的中点，∴DF ＝12AC ＝CF.∵CD ＝CF ，∴CD ＝CF ＝DF.∴△CDF 是等边三角形．∴∠ACD ＝60°.∵∠B ＝50°，∴∠BCD ＋∠BDC ＝130°.∵∠BCD 和∠BDC 的平分线相交于点E ，∴∠DCE ＋∠CDE ＝65°.∴∠CED ＝115°.∴∠ACD ＋∠CED ＝60°＋115°＝175°.第9题答图二、 填空题10. (2019，黔东南州)如图，点E 在正方形ABCD 的边AB 上．如果EB ＝1，EC ＝2，那么正方形ABCD 的面积为 3 .第10题图【解析】 由勾股定理，得BC ＝EC 2－EB 2＝ 3.∴正方形ABCD 的面积为BC 2＝3.11. (2019，东营)已知等腰三角形的底角是30°，腰长为23，则它的周长是（ 6＋43 ）.【解析】 如答图，过点A 作AD ⊥BC 于点D.∵AB ＝AC ，∴BD ＝DC.在Rt △ABD 中，∠B ＝30°，∴AD ＝12AB ＝ 3.由勾股定理，得BD ＝AB 2－AD 2＝3，∴BC ＝2BD ＝6.∴△ABC 的周长为6＋23＋23＝6＋4 3.第11题答图12. (2019，南京)无盖圆柱形杯子的展开图如图所示．将一根长为20 cm的细木筷斜放在该杯子内，木筷露在杯子外面的部分至少有 5 cm.第12题图【解析】由题意，可得杯子内细木筷的长度最长为122＋92＝15，则木筷露在杯子外面的部分至少有20－15＝5(cm)．13. (2019，北京)如图所示的网格是正方形网格，则∠P AB＋∠PBA＝45 °.(点A，B，P是网格线的交点)第13题图【解析】如答图，延长AP交格点于D，连接BD，则PD2＝BD2＝12＋22＝5，PB2＝12＋32＝10，∴PD2＋DB2＝PB2.∴∠PDB＝90°.∴∠DPB＝∠PAB＋∠PBA＝45°.第13题答图14. (2019，枣庄)把两个同样大小含45°角的三角尺按如图所示的方式放置，其中一个三角尺的锐角顶点与另一个三角尺的直角顶点重合于点A，且另外三个锐角顶点B，C，D在同一直线上．若AB＝2，则CD＝（6－2）.第14题图【解析】如答图，过点A作AF⊥BC于点F.在Rt△ABC中，∠B＝45°，∴BC＝2AB ＝22，BF＝AF＝FC＝22AB＝ 2.∵两个三角尺大小相同，∴AD＝BC＝2 2.在Rt△ADF 中，根据勾股定理，得DF＝AD2－AF2＝ 6.∴CD＝DF－FC＝6－ 2.第14题答图15. (2019，鄂州)如图，已知线段AB＝4，O是AB的中点，直线l经过点O，∠1＝60°，P是直线l上一点，当△APB为直角三角形时，则BP＝（2或23或27 ）.第15题图【解析】如答图．∵AO＝OB＝2，∠1＝60°，∴当BP1＝2时，∠AP1B＝90°.当∠P2BA ＝90°时，∵∠1＝60°，∴BP2＝OB·tan∠1＝2 3.当∠P3AB＝90°时，∵∠AOP3＝60°，∴AP3＝OA·tan∠AOP3＝2 3.∴BP3＝AB2＋AP23＝27.综上所述，当△APB为直角三角形时，BP 的长是2或23或27.第15题答图三、解答题16. (2019，大庆)如图，一艘船由A港沿北偏东60°方向航行10 km至B港，然后再沿北偏西30°方向航行10 km至C港．(1)求A，C两港之间的距离；(结果精确到0.1 km，参考数据：2≈1.414，3≈1.732)(2)确定C港在A港的什么方向．第16题图解：(1)由题意，可得∠PBC ＝30°，∠MAB ＝60°. ∴∠CBQ ＝60°，∠BAN ＝30°. ∴∠ABQ ＝30°. ∴∠ABC ＝90°. ∵AB＝BC ＝10 km ，∴AC＝AB 2＋BC 2＝102≈14.1(km)． 答：A ，C 两港之间的距离约为14.1 km. (2)由(1)知，△ABC 为等腰直角三角形， ∴∠BAC ＝45°.∴∠CAM ＝60°－45°＝15°.∴C 港在A 港北偏东15°的方向上．17. (2019，呼和浩特)如图，在△ABC 中，∠A ，∠B ，∠C 所对的边分别为a ，b ，c . (1)若a ＝6，b ＝8，c ＝12，请直接写出∠A 与∠B 的和与∠C 的大小关系； (2)求证：△ABC 的内角和等于180°；(3)若aa －b ＋c＝12（a ＋b ＋c ）c ，求证：△ABC 是直角三角形．第17题图(1)解：∠A ＋∠B ＜∠C .(2)证明：如答图，过点B 作MN ∥AC . ∵MN ∥AC ，∴∠MBA ＝∠A ，∠NBC ＝∠C .∵∠MBA ＋∠ABC ＋∠NBC ＝180°， ∴∠A ＋∠ABC ＋∠C ＝180°. 即△ABC 的内角和等于180°. (3)证明：∵aa －b ＋c ＝12（a ＋b ＋c ）c ，∴ac ＝12(a ＋b ＋c )(a －b ＋c )＝12[(a ＋c )2－b 2]．∴2ac ＝a 2＋2ac ＋c 2－b 2. ∴a 2＋c 2＝b 2.∴△ABC 是直角三角形．第17题答图1. (2019，绵阳)如图，在四边形ABCD 中，AB ∥DC ，∠ADC ＝90°，AB ＝5，CD ＝AD ＝3，E 是线段CD 的三等分点，且靠近点C ，∠FEG 的两边与线段AB 分别相交于点F ，G ，连接AC 分别交EF ，EG 于点H ，K .若BG＝32，∠FEG ＝45°，则HK 的长是(B )第1题图A.223B. 526C. 322D. 1326【解析】 ∵∠ADC ＝90°，CD ＝AD ＝3，E 是CD 的三等分点，∴AC ＝32，CE ＝1，DE ＝2.∵AB ＝5，BG ＝32，∴AG ＝72.∵AB ∥DC ，∴△CEK ∽△AGK.∴CE AG ＝CK AK ＝EK KG .∴172＝CKAK＝EK KG .∴CK AK ＝EK KG ＝27.∵CK ＋AK ＝32，∴CK ＝223.如答图，过点E 作EM ⊥AB 于点M ，则四边形ADEM 是矩形．∴EM ＝AD ＝3，AM ＝DE ＝2，∴MG ＝32.∴EG ＝EM 2＋MG 2＝352.∵EK KG ＝27，∴EK ＝53.∵∠HEK ＝∠KCE ＝45°，∠EHK ＝∠CHE ，∴△HEK ∽△HCE.∴HC HE ＝HE HK＝CE EK ＝153＝35.∴设HE ＝3x ，HK ＝5x.∴5x ＋2233x ＝35.解得x ＝106.∴HK ＝526.第1题答图2. (2019，齐齐哈尔)在等腰三角形ABC 中，BD ⊥AC ，垂足为D ，且BD ＝12AC ，则等腰三角形ABC 底角的度数为 15°或45°或75°.【解析】 本题分三种情况．①如答图①，当点B 是顶角顶点时，∵AB ＝BC ，BD ⊥AC ，∴AD ＝CD.∵BD ＝12AC ，∴BD ＝AD ＝CD.在Rt △ABD 中，∠A ＝∠ABD ＝12×(180°－90°)＝45°.②如答图②，当点B 是底角顶点，且BD 在△ABC 外部时，∵BD ＝12AC ，AC ＝BC ，∴BD ＝12BC.∴∠BCD ＝30°.∴∠ABC ＝∠BAC ＝12×30°＝15°.③如答图③，当点B 是底角顶点，且BD 在△ABC 内部时，∵BD ＝12AC ，AC ＝BC ，∴BD ＝12BC.∴∠C ＝30°.∴∠ABC ＝∠BAC ＝12×(180°－30°)＝75°.综上所述，等腰三角形ABC 底角的度数为15°或45°或75°.第2题答图3. (2019，湖州南浔区二模)【尝试探究】如图①，等腰直角三角形ABC 的两个顶点B ，C 在直线MN 上，D 是直线MN 上一个动点(点D 在点C 的右边)，BC ＝3，BD ＝m ，在△ABC 同侧作等腰直角三角形△ADE ，∠ABC ＝∠ADE ＝90°，EF ⊥MN 于点F ，连接CE .(1)求DF 的长；(2)在判断AC ⊥CE 是否成立时，小明同学发现可以由以下两种思路解决此问题． 思路一：先证CF ＝EF ，求出∠ECF ＝45°，从而证得结论成立．思路二：先求DF ，EF 的长，再求CF 的长，然后证AC 2＋CE 2＝AE 2，从而证得结论成立．请你任选一种思路，完整地书写本小题的证明过程． 【拓展探究】(3)如图②，将图①中的两个等腰直角三角形都改为有一个角为30°的直角三角形，∠ABC ＝∠ADE ＝90°，∠BAC ＝∠DAE ＝30°，BC ＝3，BD ＝m .判断AC ⊥CE 是否成立，并说明理由．第3题图(1)解：∵△ABC 和△ADE 都是等腰直角三角形，∠ABC ＝∠ADE ＝90°， ∴AB ＝BC ，AD ＝DE ，∠ADB ＋∠EDF ＝90°. ∵EF ⊥MN ，∴∠DEF ＋∠EDF ＝90°. ∴∠ADB ＝∠DEF .在△ABD 和△DFE 中，⎩⎪⎨⎪⎧∠ADB ＝∠DEF ，∠ABD ＝∠DFE ＝90°，AD ＝DE ，∴△ABD ≌△DFE (AAS)．∴DF＝AB＝BC＝3.(2)证明：思路一：由(1)，得△ABD≌△DFE，∴DF＝AB＝BC＝3，EF＝BD＝m.∴CF＝CD＋DF＝CD＋BC＝BD＝m.∴CF＝EF.∵EF⊥MN，∴∠ECF＝45°.∵∠ACB＝45°，∴∠ACE＝90°，即AC⊥CE.思路二：由(1)，得△ABD≌△DFE，DE＝AD.∴DF＝AB＝BC＝3，EF＝BD＝m.∴CF＝CD＋DF＝CD＋BC＝BD＝m.由勾股定理，得DE2＝DF2＋EF2＝32＋m2＝9＋m2.∴AE2＝2DE2＝2(9＋m2)．∵AC2＝32＋32＝18，CE2＝CF2＋EF2＝2m2，∴AC2＋CE2＝AE2.∴∠ACE＝90°，即AC⊥CE.(3)解：AC⊥CE成立．理由：如答图，过点E作EF⊥MN. ∴∠DEF＋∠EDF＝90°.∵∠ADE＝90°，∴∠ADB＋∠EDF＝90°.∴∠ADB＝∠DEF.∵∠ABC＝∠EFD＝90°，∴△ABD∽△DFE.∴EFBD＝DFAB＝DEAD＝tan∠DAE＝tan 30°＝33.∴EF＝3m 3.∵∠BAC＝30°，BC＝3，∴AB＝3 3.∴DF＝33AB＝3.∴DF＝BC.∴CF＝CD＋DF＝CD＋BC＝BD＝m.∴在Rt△CEF中，tan∠ECF＝EFCF＝3 3.∴∠ECF＝30°.∵∠ACB＝90°－∠BAC＝90°－30°＝60°，∴∠ACE＝90°，即AC⊥CE.第3题答图。

2021年中考数学一轮复习《三角形认识》基础复习题1.将一副三角尺按如图方式进行摆放，∠1、∠2不一定互补的是（）2.如图，在正方形ABCD中，E为DC边上的一点，沿线段BE对折后，若∠ABF比∠EBF大15°，则∠EBF的度数是（）A.15°B.20°C.25°D.30°3.如图，一副三角板（直角顶点重合）摆放在桌面上，若∠AOD=150°，则∠BOC等于（）A.30°B.45°C.50°D.60°4.一个角等于它的补角的5倍，那么这个角的补角的余角是（）A.30°B.60°C.45°D.150°5.如图，直线a∥b，将一块含30°角(∠BAC=30°)的直角三角尺按图中方式放置，其中A和C 两点分别落在直线a和b上．若∠1=20°，则∠2的度数为( )A．20° B．30° C．40° D．50°6.如图，直线l1∥l2，CD⊥AB于点D，∠1=50°，则∠BCD的度数为（）A.50°B.45°C.40°D.30°7.如图,下列条件不能判断直线l1∥l2的是( )A.∠1＝∠3B.∠1＝∠4C.∠2＋∠3＝180°D.∠3＝∠58.如图，点E在CD的延长线上，下列条件中不能判定AB∥CD的是（）A.∠1=∠2B.∠3=∠4C.∠5=∠BD.∠B+∠BDC=180°9.如图，AD⊥BC于D，BE⊥AC于E，CF⊥AB于F，GA⊥AC于A，则△ABC中，AC边上的高为( )A.ADB.GAC.BED.CF10.如图，已知在正方形网格中，每个小方格都是边长为1的正方形，A，B两点在小方格的顶点上，位置如图所示，点C也在小方格的顶点上，且以A，B，C为顶点的三角形面积为1，则点C的个数为（）A.3个B.4个C.5个D.6个11.三条线段a,b,c长度均为整数且a=3,b=5.则以a,b,c为边的三角形共有( )A.4个B.5个C.6个D.7个12.三角形两边长为6与8，那么周长L的取值范围（）A.2<L<14B.16<L<28C.14<L<28D.20<L<2413.为估计池塘两岸A，B间的距离，杨阳在池塘一侧选取了一点P，测得PA=16m，PB=12m，那么AB间的距离不可能是（）A．15m B．17m C．20m D．28m14.已知△ABC的边长分别为a，b，c，化简|a+b﹣c|﹣|b﹣a﹣c|的结果是（）A.2aB. 2b-2cC.2a+3bD. -2b15.已知三角形三边长分别为2，x，13，若x为正整数，则这样的三角形个数为（）A.2B.3C.5D.1316.如图，在△ABC中AC=BC，点D和E分别在AB和AC上，且AD=AE．连接DE，过点A的直线GH与DE平行，若∠C=40°，则∠GAD的度数为( )A．40° B．45° C．55° D．70°17.将一副三角板，如图所示放置，使点A落在DE边上，BC∥DE，AB与EF相交于点H，则∠AHF 的度数为（）A.30°B.45°C.60°D.75°18.如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=（）A.35°B.95°C.85°D.75°19.如图，直线a∥b,直角三角形如图放置，∠DCB=90°，若∠1+∠B=70°，则∠2的度数为( )A.20°B.40°C.30°D.25°20.下列条件：①∠A+∠B=∠C，②∠A∶∠B∶∠C=2∶3∶4，③∠A=90°-∠B，④∠A=∠B= ∠C 中.能确定△ABC是直角三角形的条件有( )A.1个B.2个C.3个D.4个21.如图，在直角三角形ABC中，AC≠AB，AD是斜边上的高，DE⊥AC，DF⊥AB，垂足分别为E.F，则图中与∠C(∠C除外)相等的角的个数是( )A.3个B.4个C.5个D.6个22.如图，在△AB C中，∠A=60°，∠ABC=50°，∠B.∠C的平分线相交于F，过点F作DE∥BC，交AB于D，交AC于E，那么下列结论正确的是( )①∠ACB=70°；②∠BFC=115°；③∠BDF=130°；④∠CFE=40°；A.①②B.③④C.①③D.①②③23.如图，Rt△ABC中，∠ACB=90°，∠A=50°，将其折叠，使点A落在边CB上A′处，折痕为CD，则( )A.40°B.30°C.20°D.10°24.若一个三角形三个外角之比为2：3：4，则与之对应的三个内角度数比为( ).A.4：3：2B.3：2：4C.5：3：1D.3：1：525.如果在△ABC中，∠A=70°-∠B，则∠C等于( )A.35°B.70°C.110°D.140°26.小明同学把一个含有450角的直角三角板在如图所示的两条平行线m,n上，测得，则的度数是( )A.450B.550C.650D.75027.如图所示，BD平分∠ABC，DE∥BC，且∠D=30°，则∠AED的度数为（）。