江苏省铜山区清华中学九年级数学上册 2.6 正多边形与圆导学案(2)(无答案)(新版)苏科版

2.6 正多边形与圆教学目标了解正多边形和圆的有关概念；会应用多边形和圆的有关知识画多边形．重难点、关键1．重点：讲清正多边形和圆之间的关系．2．难点与关键：讲清正多边形和圆之间的关系．教学过程一、复习引入请同学们口答下面两个问题．1．什么叫正多边形？2．从你身边举出两三个正多边形的实例，正多边形具有轴对称、•中心对称吗？其对称轴有几条，对称中心是哪一点？二、探索新知如果我们以正多边形对应顶点的交点作为圆心，过点到顶点的连线为半径，能够作一个圆，很明显，这个正多边形的各个顶点都在这个圆上，如图，正六边形ABCDEF，连结AD.CF交于一点，以O为圆心，OA为半径作圆，那么肯定B.C.D.E.F都在这个圆上．因此，正多边形和圆的关系十分密切，只要把一个圆分成相等的一些弧，就可以作出这个圆的内接正多边形，这个圆就是这个正多边形的外接圆．我们以圆内接正六边形为例证明．如图所示的圆，把⊙O•分成相等的6段弧，依次连接各分点得到六边ABCDEF，下面证明，它是正六边形．∵AB=BC=CD=DE=EF又∴∠A =BCF =（BC +CD +DE +EF ）=2BC ∠B =CDA =（CD +DE +EF +FA ）=2CD ∴∠A =∠B同理可证：∠B =∠C =∠D =∠E =∠F =∠A又六边形ABCDEF 的顶点都在⊙O 上∴根据正多边形的定义，各边相等、各角相等、六边形ABCDEF 是⊙O 的内接正六边形，⊙O 是正六边形ABCDEF 的外接圆．例 1 如图2-56，正六边形ABCDEF 的半径为4，求这个正六边形的周长和面积.解：作半径OA.OB ，根据题意，得∠A =3606︒=60° ∵OA =OB ，∴△OAB 为等边三角形，AB =OA =4.正六边形的周长l =4×6=24.过点O 作OG ⊥AB ，垂足为G .在Rt △OAG 中，∵OA =4，AG =12AB =2， ∴OG==正六边形的面积S =12×4×例2利用你手中的工具画一个边长为3cm 的正五边形．【解析】要画正五边形，首先要画一个圆，然后对圆五等分，因此，应该先求边长为3的正五边形的半径．解：正五边形的中心角∠AOB ==72°， 121212123605︒如图，∠AOC =30°，OA =AB ÷sin36°=1.5÷sin36°≈2.55（cm ）画法（1）以O 为圆心，OA =2.55cm 为半径画圆；（2）在⊙O 上顺次截取边长为3cm 的AB.BC.CD.DE.EA ．（3）分别连结AB.BC.CD.DE.EA ．则正五边形ABCDE 就是所要画的正五边形，如图所示．三、巩固练习教材练习题．四、归纳小结（学生小结，老师点评）12。

2.6 正多边形与圆-苏科版九年级数学上册教案一、教学目标1.了解正多边形和圆的基本概念，掌握相关术语和符号。

2.理解正多边形与圆的关系，掌握计算正多边形的周长和面积的方法。

3.能够分析解决实际问题，应用正多边形和圆的相关知识。

二、教学重难点教学重点：正多边形和圆的基本概念，正多边形与圆的关系。

教学难点：计算正多边形的周长和面积的方法，应用正多边形和圆的相关知识解决实际问题。

三、教学内容及任务1. 正多边形的定义和特征正多边形指边数相等、每个内角相等的多边形。

教师通过展示图形让学生感知正多边形的基本特征，让学生亲自制作正三角形、正四边形、正五边形等多边形，感受不同的边数对正多边形形态的影响。

任务一：观察图形，描述正多边形的几何特征。

任务二：制作正三角形、正四边形、正五边形，计算它们的内角和。

2. 正多边形的周长和面积教师通过示范计算正多边形的周长和面积的方法，让学生掌握相关计算公式和技巧。

任务三：计算一个正六边形的周长和面积。

任务四：比较正十二边形和正十六边形的面积大小。

3. 圆的定义和性质圆指平面上所有到圆心距离相等的点的集合。

教师通过图形展示让学生感知圆的基本性质，例如直径、半径、圆心角、圆周角等术语和符号。

任务五：观察图形，描述圆的几何特征。

任务六：计算一个直径为8厘米的圆的周长和面积。

4. 正多边形与圆教师将正多边形和圆进行比较，讲解它们的关系和联系，以及正多边形内切于圆的情况下，正多边形的边数与圆的半径和面积的关系。

任务七：计算一个内切于半径为5厘米的圆的正五边形的边长和面积。

任务八：设计一道数学问题，涉及到正六边形和圆的相关知识。

四、课堂练习1. 基础练习1.计算一个正七边形的内角和。

2.计算一个直径为12厘米的圆的半径和面积。

3.计算一个内切于半径为10厘米的圆的正六边形的边长和面积。

2. 拓展练习1.设计一道数学问题，描述一个本来很长的细木条能不能通过一个直径为6厘米的圆形洞。

2.设计一道数学问题，涉及到正五边形和圆的相关知识。

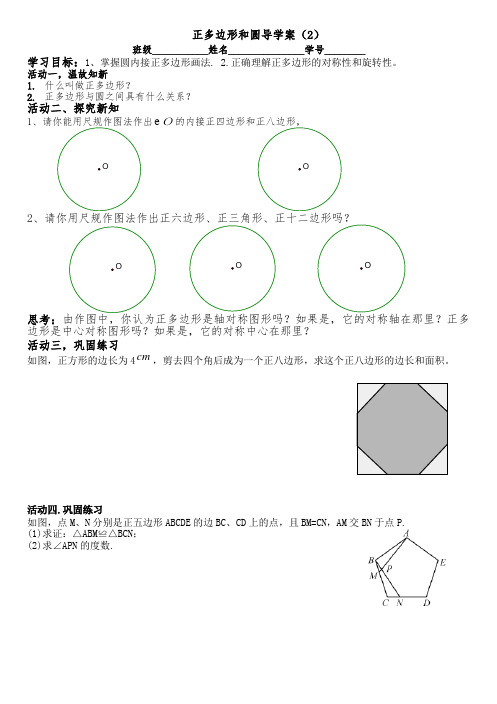
正多边形和圆导学案（2）班级___________姓名_______________学号________学习目标：1、掌握圆内接正多边形画法. 2.正确理解正多边形的对称性和旋转性。

活动一，温故知新1.什么叫做正多边形？2.正多边形与圆之间具有什么关系？活动二、探究新知1O2思考：边形是中心对称图形吗？如果是，它的对称中心在那里？活动三，巩固练习如图，正方形的边长为4cm，剪去四个角后成为一个正八边形，求这个正八边形的边长和面积。

活动四.巩固练习如图，点M、N分别是正五边形ABCDE的边BC、CD上的点，且BM=CN，AM交BN于点P.(1)求证：△ABM≌△BCN；(2)求∠APN的度数.活动五，课外作业1.下面图形中，是正多边形的是( )A.矩形B.菱形C.正方形D.等腰梯形2.如图，正六边形的每一个内角都相等，则其中一个内角α的度数是( )A.240°B.120°C.60°D.30°3. 如图为2012年伦敦奥运会纪念币的图案，其形状近似看作为正七边形，则一个内角为 度.4.一个正多边形的一个外角等于30°，则这个正多边形的边数为 .5.如图，一束平行太阳光线照射到正五边形上，则∠1= .第2题图 第3题图 第5题图 第6题图6.如图，AD 是正五边形ABCDE 的一条对角线，则∠BAD= .7.若正方形的边长为6，则其外接圆半径与内切圆半径的大小分别为( )A.6，32B.32，3C.6，3D.62,328.正六边形的边心距与边长之比为( ) A.3∶3 B.3∶2 C.1∶2 D.2∶29.如图，边长为a 的正六边形内有两个三角形(数据如图)，则空白阴影S S =( ) A.3 B.4 C.5 D.6 第9题图 第10题图10.将一个边长为1的正八边形补成如图所示的正方形，这个正方形的边长等于 (结果保留根号).11.若一个正六边形的周长为24，求该正六边形的面积.(结果保留根号)12.如图所示，正五边形ABCDE 的对角线AC 和BE 相交于点M.求证：(1)AC ∥DE ；(2)ME=AE。

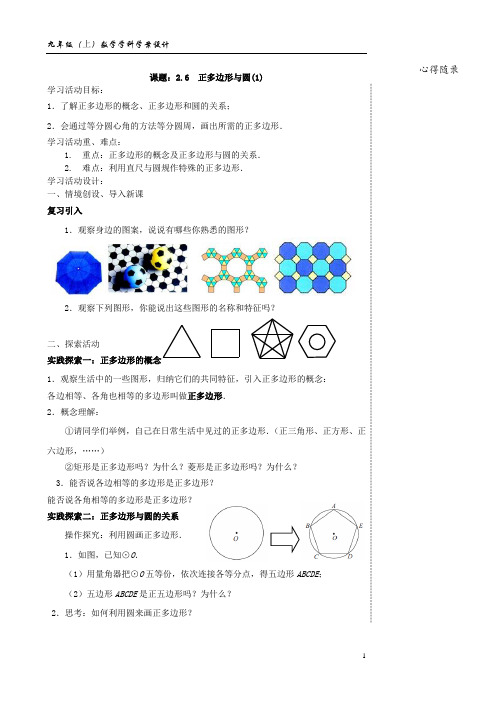
课题：2.6 正多边形与圆(1)学习活动目标：1．了解正多边形的概念、正多边形和圆的关系；2．会通过等分圆心角的方法等分圆周，画出所需的正多边形．学习活动重、难点：1.重点：正多边形的概念及正多边形与圆的关系．2.难点：利用直尺与圆规作特殊的正多边形．学习活动设计：一、情境创设、导入新课复习引入1．观察身边的图案，说说有哪些你熟悉的图形？2．观察下列图形，你能说出这些图形的名称和特征吗？二、探索活动实践探索一：正多边形的概念1．观察生活中的一些图形，归纳它们的共同特征，引入正多边形的概念：各边相等、各角也相等的多边形叫做正多边形．2．概念理解：①请同学们举例，自己在日常生活中见过的正多边形．（正三角形、正方形、正六边形，……）②矩形是正多边形吗？为什么？菱形是正多边形吗？为什么？3．能否说各边相等的多边形是正多边形？能否说各角相等的多边形是正多边形？实践探索二：正多边形与圆的关系操作探究：利用圆画正多边形．1．如图，已知⊙O．（1）用量角器把⊙O五等份，依次连接各等分点，得五边形ABCDE；（2）五边形ABCDE是正五边形吗？为什么？2．思考：如何利用圆来画正多边形？数学实验室：3．如图，点A 、B 、C 、D 、E 、F 六等分⊙O ．（1）在一张透明纸上画与下图形状、大小相同的图形，并把它们叠合在一起；（2）把所画图形绕点O 旋转60°，你发现了什么？再旋转60°呢？你能从图形运动的角度说明六边形ABCDEF 是正六边形吗？4．请你思考一下：正六边形与圆有何关系？相关概念：一般地，用量角器把一个圆n （n ≥3）等分，依次连接各等分点所得的多边形是这个圆的内接正多边形．正多边形的外接圆的圆心叫做正多边形的中心，外接圆的半径叫做正多边形的半径．三、深入探讨例1 在等边三角形ABC 中，E 、F 、G 、H 、L 、K 分别是各边三等分点，试说明六边形EFGHLK 是正六边形．例2 如图，正六边形ABCDEF 的半径为4．求这个正六边形的周长和面积．四、习得展示与检验1．下列说法中正确的是( )．A ．平行四边形是正多边形；B ．矩形是正四边形；C ．菱形是正四边形；D ．正方形是正四边形；2．若一个正多边形的每个内角为150°，则这个正多边形的边数为 ．3．已知正四边形的外接圆的半径为R ，则正四边形的周长是 ．五、小结、拓展延伸1．这节课你有哪些收获和困惑？2．如何画一个正多边形？3.课本P81第1、2、3、4．阅读课本P81：判定正多边形的条件．六、教后反思AE C BFGH KL。

新苏科版九年级数学上册2.6正多边形与圆学案班级______学号_____姓名___________学习目标：1．知道正多边形的概念、正多边形和圆的关系，会判定一个正多边形是轴对称图形还是中心对称图形．2．会用量角器画正多边形，会用直尺和圆规画特殊的正多边形．学习重点：正多边形的概念及其对称性；利用正多边形与圆的关系，解决有关作图问题． 学习难点：利用直尺与圆规作特殊的正多边形．一、学前准备：1．如图，点A 、B 、C 、D 在⊙O 上，AB ⌒ = DC ⌒ ．AC 与BD 相等吗？为什么？2．如图，CD 是⊙O 的直径， AB 为弦，CD ⊥AB 于点F ，且AB = 16cm ，CE = 4cm ．求⊙O 的半径．3．将 AB ⌒ 4等份．二、探究活动独立思考·解决问题活动（一）1．日常生活中，我们经常看到如下图所示的多边形．2．观察下列图形，你能说出这些图形的名称和边、角特征吗？活动（二）探索正多边形和圆的关系1.用量角器将一个圆n （n 为≥3的整数，你自己取一个值）等分；2.依次连接各等分点；3.你得到什么图形？4.这个图形与⊙O 有什么样的关系？师生探究·合作交流活动（三）探索正多边形的对称性1．下列多边形是轴对称图形还是中心对称图形.（请写一写）并分别画出对称轴、指出对称中心.2.观察上面的多边形的边数和对称性，他们有哪些共同的特点.活动（四）利用圆规和直尺作特殊的正多边形在下列的圆中你能用尺规分别作出正四边形、正八边形、正三角形、正六边形.三、学习体会1．本节课你有哪些收获？ 2．预习时的疑难解决了吗？你还有哪些疑惑？四、自我测试1．正方形ABCD的外接圆圆心O叫做正方形ABCD的______．2．正多边形一定是对称图形，一个正n边形共有条对称轴，每条对称轴都通过；如果一个正n边形是中心对称图形，n一定是．3．将一个正五边形绕它的中心旋转，至少要旋转度，才能与原来的图形位置重合。

新苏科版九年级数学上册2-6正多边形和与圆导学案【知识扫描】1、弧长公式在半径为R的圆中，n°的圆心角所对的弧长l的计算公式为2、扇形面积公式（1）在半径为R的圆中，圆心角为n°的扇形面积的计算公式为（2）在半径为R的圆中，弧长为l的扇形面积S的计算公式为注：在半径R，圆心角n，弧长l，扇形面积S，以知其中任意两个量，都可以求出其余的两个量。

【基础训练】1．在半径为3cm的圆中，60°的圆心角所对的弧长是 cmπ，则这条弧所对的圆心角＝2.一个圆的半径为3，圆上的一条弧的长为123．圆心角为60°，半径为6cm的扇形的面积为4．已知扇形的圆心角为120°，弧长是20π cm，扇形的面积为5．若扇形的面积为3π，弧长为2π，则半径为，圆心角是6.若半径为5cm的一段弧长等于半径为2cm的圆的周长，则该所对的圆心角为7.△ABC 的外接圆半径为2,∠BAC=60゜,则∠BAC 所对的弧BC的长为8.如图, ⊙O的半径为5,A 是⊙O外一点,AB 切⊙O于点B,AO交⊙O于点C,AC=OC, 求(1)弧BC的度数;(2)图中阴影部分的面积S (精确到0.1)BOACDEO AO D C BA 9．如图，AB 是⊙O 的直径，点D ，E 是半圆的三等分点，AE ，BD 的延长线交于点C ，且CE=2，求阴影部分的面积.【拓展视野】10.两个同心圆中，大圆的半径OA 、OB 交小圆于C 、D ，OC ：CA=3：2，则弧CD 与弧AB 的长度之比为 ( ) A 、32 B 、 23 C 、35 D 、 5311.若⊙A 的60°的弧与⊙B 的45°的弧的长度相等，则⊙A 与⊙B 的面积之比为 ( ) A 、 34 B 、 43 C 、 916 D 、 16912．如图，是一幅小地毯的图案设计，外侧大正方形的边长是1米，在里面画两条对角线、一个圆、两个正方形，阴影部分的面积是0.26平方米，则最小的正方形的边长为_____米。

授课标题正多边形与圆学习目标1.结合本节课的教学内容培养学生亲自动手实验，学会观察图形，主动获得知识的力．2.了解正多边形的概念、正多边形与圆的关系;3.会通过等分圆心角的方法等分圆周，画出所需的正多边形；4.会用直尺和圆规画一些特殊的正多边形.重点难点1.了解正多边形的概念、正多边形与圆的关系;2.会通过等分圆心角的方法等分圆周，画出所需的正多边形；3.会用直尺和圆规画一些特殊的正多边形.一、知识点（一）三角形的外接圆和内切圆（1）不在上的个点确定一个圆.（2）三角形的外接圆：经过三角形的三个顶点可以做一个圆，这个圆叫做三角形的外接圆，这个三角形叫做三角形.三角形外接圆的圆心是三角形三条边线的交点，叫做这个三角形的．（3）三角形的内切圆：与三角形各边都的圆叫做三角形的内切圆，这个三角形叫做三角形.三角形内切圆的圆心是三角形三条的交点，叫做三角形的．（二）圆与正多边形顺次连接圆上的n 点得到的多边形是正n边形．（1）一个正多边形的各个顶点都在圆上，这个圆是这个正多边形的圆；把一个正多边形的外接圆的叫做这个正多边形的中心；外接圆的叫做正多边形的半径；正多边形每一边所对的圆心角叫正多边形的角；中心到正多边形的一边的叫做正多边形的边心距．（2）圆内接四边形的对角．（3）圆内接正n边形都是图形，有条对称轴.圆内接正2n边形是图形，对称中心是正多边形的，即外接圆的圆心．（4）任何一个正多边形都有一个外接圆和一个内切圆，它们是圆．（5）常见圆的内接正多边形半径与正多边形边心距的关系：设正n边形的半径为r，边心距为d．（1）圆内接正三角形中，r= 或d= r；（2）圆内接正四边形中，r= d或d= r；（3）圆内接正六边形中，d= r．二、经典例题例1.（1）下列命题中,真命题是①各边都相等的多边形是正多边形; ②各角都相等的多边形是正多边形;③正多边形一定是中心对称图形; ④边数相同的正多边形一定相似.例 2.若一个正多边形绕它的中心旋转90°就和原来的图形重合,则这个正多边形是( )A.正三角形B.正方形C.正五边形D.正六边形例3.如图，正六边形螺帽的边长是2cm，这个扳手的开口a的值应是（）A．32 cm B．3cm C．332 cm D．1cm例4．如图，圆内接正五边形ABCDE中，对角线AC和BD交于点P，则∠APB=________.例5.如图，已知⊙O过正方形ABCD的顶点A、B，且与CD边相切，若正方形的边长为2，则圆的半径为（）A．43B.545例6.正方形ABCD的边长为2，则其外接圆半径等于_____；内切圆的半径等于_____。

课题 2.6正多边形与圆自主空间学习目标1.了解正多边形的概念、正多边形和圆的关系，会判定一个正多边形是中心对称图形还是轴对称图形2.会通过等分圆心角的方法等分圆周，画出所需的正多边形3.能够用直尺和圆规作图，作出一些特殊的正多边形学习重难点正多边形的概念及正多边形与圆的关系、利用直尺与圆规作特殊的正多边形教学流程预习导航1.观察下列图形，你能说出这些图形的特征吗？2.矩形有上述特征？菱形有上述特征吗？3.经过预习，你能说出正多边形的定义吗？合作探究一、概念探究：1.探索正多边形的概念（1）观察生活中的一些图形，归纳它们的共同特征，引入正多边形的概念：各边相等、各角也相等的多边形叫做正多边形。

（2）概念理解：①请同学们举例，自己在日常生活中见过的正多边形．（正三角形、正方形、正六边形，…….）②矩形是正多边形吗？为什么？菱形是正多边形吗？为什么？（3）正n边形的每个内角等于多少度？每个外角呢？2.探索正多边形与圆的关系（1）你能借助量角器，利用圆来画正三角形吗？正方形呢？正五边形呢？正六边形呢？…….学会利用量角器等分圆周的方法画正多边形。

（2）引入圆的内接正多边形：正多边形的外接圆：正多边形的中心：3.探索正多边形的对称性（1）图中的正多边形，哪些是轴对称图形？哪些是中心对称图形？哪些既是轴对称图形，又是中心对称图形？如是轴对称图形，画出它的对称轴；如是中心对称图形，找出它的对称中心。

（如果一个正多边形是中心对称图形，那么它的中心就是对称中心。

）（2）任何一个正多边形既是轴对称图形，又是中心对称图形吗？跟边数有何关系？合作探究4.探索用直尺和圆规作出正方形，正六多边形的方法。

（1）作正四边形：在圆中作两条互相垂直的直径，依次连结四个端点所得图形（然如何作正八边形？作正十六边形？……）（2）作正六边形：在圆中任作一条直径，再以两端点为圆心，相同的半径为半径作弧与圆相交，依次连结圆上的六个点所得图形（任何作正三角形？正十二边形？……）二、例题分析：1.已知：如图，正三角形，求作：正三角形ABC的外接圆和内切圆。

2.6正多边形和圆教学目标：1.知道正多边形的概念、正多边形与圆的关系；2.会画正多边形，会判定一个正多边形是轴对称图形还是中心对称图形；3.经历探索画正多边形的过程中，学会等分圆的方法.教学重难点：1.会画正多边形.2.通过阅读、探索，会用量角器和尺规画正多边形.【预习导航】1、的多边形叫做正多边形。

2、把圆分成n（n≥3）等份：依次连结各分点所得的多边形是这个圆的；3、由正多边形的定义可以知道正n边形的每个内角都相等，每个外角也相等，由于正n边形的内角和为，所以，正n边形的每个内角都等于，由于n边形的外角和是，所以，正n边形的每个外角都等于。

4、图中的正多边形，哪些是轴对称图形？哪些是中心对称图形？哪些既是轴对称图形，又是中心对称图形？如是轴对称图形，画出它的对称轴；如是中心对称图形，找出它的对称中心。

思考：任何一个正多边形既是轴对称图形，又是中心对称图形吗？跟边数有何关系？【课堂探究】问题1：如图，有一个亭子，它的地基是半径为4cm的正六边形，求地基的周长和面积(精确到0.1cm2)。

第1 页共3 页第 2 页 共 3 页问题2：如图，正六边形ABCDEF 的半径为8cm ，求这个正六边形的边长。

问题3：如图，正三角形的半径为R ，则边长为 ，边心距为 ，面积为 。

问题4：正三角形的边长a ，则其半径为 。

【课堂检测】班级 学号 姓名 等第1、若正多边形的内角和是540度，那么这个正多边形是正 边形。

2、一个外角等于一个内角的32的正多边形是正 边形。

3、正方形的内切圆半径、外接圆半径、边长之比为________________。

4、正六边形的一个内角是_________度，若它的边长为1，则面积为_______________。

5、求证：正五边形的对角线相等。

已知：求证：7、圆内接正五边形的对角线AC 、BE 相交于点M 。

求证：（1）ME=AB ；（2）ME 2=BE ·BM 。