图与网络分析例题讲解
- 格式:doc
- 大小:222.00 KB
- 文档页数:7










《运筹学》第八章图与网络分析习题1.思考题(1)解释下列名词,并说明相互之间的区别与联系:①顶点,相邻,关联边;②环,多重边,简单图;③链,初等链;④圈,初等圈,简单拳;⑤ 回 路,初等路;⑥节点的次,悬挂点,孤立点;⑦)连通图,连同分图, 支 撑子图;⑧有向图,基础图,赋权图。
⑨子图,部分图,真子图.(2)通常用记号G=(V,E)表示一个图,解释V及E的涵义及这个表达式 的涵义.(3)通常用记号D=(V,A)表示一个有向图,解释V及A的涵义及这个表 达式的涵义.(4) 图论中的图与一般几何图形的主要区别是什么? (5) 试述树与图的区别与联系.(6) 试述 求最短路问题的Dijkstra 算法的基本思想及其计算步骤. (7) 试述寻求最大流的标号法的步骤与方法.(8) 简述最小费用最大流的概念及其求解的基本思想和方法.(9) 通常用记号N=(V,A,C)表示一个网络,试解释这个表达式的涵义. (10) 在最大流问题中,为什么当存在增广链时,可行流不是最大流? (11) 试叙述最小支撑树、最大流、最短路等问题能解决那些实际问题。
2.判断下列说法是否正确(1) 图论中的图是为了研究问题中有哪些对象及对象之间的关系,它与图的几何形状无关。
(2) 一个图G 是树的充分必要条件是边数最少的无孤立点的图。
(3) 如果一个图G 从V 1到各点的最短路是唯一的,则连接V 1到各点的最短路,再去掉重复边,得到的图即为最小支撑树。
(4 )图G 的最小支撑树中从V 1到V n 的通路一定是图G 从V 1到V n 的最短路。
(5) {f ij =0}总是最大流问题的一个可行流。
(6 )无孤立点的图一定是连通图。
(7) 图中任意两点之间都有一条简单链,则该图是一棵树。
(8) 求网络最大流的问题总可以归结为求解一个线性规划问题。
(9)在图中求一点V1到另一点Vn 的最短路问题总可以归结为一个整数规划问题 (10) 图G 中的一个点V 1总可以看成是G 的一个子图。
实验六:图与网络分析-最短路问题
一、实验目的:掌握不同问题的输入方法,求解网络模型,观察求解步骤,显示并读出结果。
二、内容和要求:用WinQSB软件求解最短路问题,并对结果进行简单分析。
例:求下图的最短路。
三、操作步骤:
1.“开始”菜单→“winQSB”→“Network Modeling”(网络模型)。
2.建立新问题:File→New Problem,出现下面界面。
选择Shortest Path Problem、Minimization、输入问题标题、节点的个数,然后单击“OK”。
3.修改节点名称:菜单“Edit”→“Node Names”,编辑完点“OK”,如下图。
4.按下图输入图的权矩阵,本例是无向图,每一条边必须输入两次。
5.菜单“Solve and Analyze”→“Solve the Problem”,出现以下对话框,
6.然后选择起点v1和终点v10,点“Solve”按键,出现下图:
从图中可以看到v1到v10的最短路径为v1→v3→v7→v10,总长为6,另外从v1到其他各点的最短距离也都计算了出来。
7.实例求解:有九个城市v1,v2…,v9,其公路网如下图,弧旁数字是该段公路的长度,有一批货物从v1运到v9,试用Dijkstra方法求出走哪条路最短?
自己先用标号法求出最短路,然后用winWSB软件进行验证。
8.思考题:教育部门打算在某新建城区建一所学校,让附近七个居民区的学生就近入学。
七个居民区之间的道路如下图所示,学校应建在哪个居民区,才能使大学都方便?(图中距离单位:百米)。
图与网络分析例题讲解————————————————————————————————作者:————————————————————————————————日期:图与网络分析例题讲解例1求救信号的采集问题紧急呼救电话发挥着极其重要的作用,现在的问题是往往在呼救时当事者大多处于紧张或身体状况不佳的状态,难以清晰表达自己所处位置,给救援工作带来极大的困难,对于有线电话来说,定位相对容易,而对于移动设备由于其可移动性,则确定位置相对比较困难。
一种可行的办法是依赖通信基站,按照移动设备接收附近几个基站信号强弱进行定位。
区域内的某个点接收到各基站的信号强度组成一个向量,该向量唯一标志区域内的一个点。
采用这种方法定位就需要采集区域内各点的信号强度,派遣一辆装载信号采集设备和GPS 的车辆,从研究所出发,依次到达各主要地点采集信号,最后回到研究所提交数据。
考察某大城市的一个特定区域,示意图共5个节点。
主要信号采集点在图中已标出(即图中的节点),如何选择一条最短路线,使得信号采集车辆能够顺利地采集信号并返回研究所。
图的邻接矩阵为:01412710140913512906871360111058110⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦。
0100000100100000000100010H ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦解 该问题实际上就是一个TSP (旅行商问题),要求寻找遍历图中所有节点,并返回起点的最短路。
TSP 属于组合优化的范畴,可以采用组合优化的方法求解TSP 。
设ij d 表示,i j 两个城市之间的距离,决策变量是0ij x =或1(0表示不连接,1表示连接),由ij x 组成的邻接矩阵H 是图G 的哈密顿圈等价于H 中每个节点都只有一个入度和一个出度,且去掉任何一个节点H 将不是圈。
此时求解TSP 就等价于求解下面0-1规划问题:,min ij iji j Vz dx ∈=∑1()..1()0,1(,)ij j V ij i Vij x i V s t x j V x i j V ∈∈⎧=∈⎪⎪=∈⎨⎪⎪=∈⎩∑∑ (1) 对于模型(1)容易用LINGO 软件求解,其程序如下:model : sets :city/1..5/:u; !Hamilton 路标号;link(city,city):distance,x; !邻接矩阵和决策矩阵; endsets data : distance=0 14 12 7 1014 0 9 13 512 9 0 6 87 13 6 0 1110 5 8 11 0;enddatan=@size(city);min=@sum(link:distance*x);@for(city(i):u(i)>=1); !城市编号非负约束;@for(city(k):@sum(city(i)|i#ne#k:x(i,k))=1; !入度为1约束;@sum(city(j)|j#ne#k:x(k,j))=1; !出度为1约束;@for(city(j)|j#gt#1#and#j#ne#k:u(j)>=u(k)+x(k,j)-n*(1-x(k,j))+(n-1)*x(j,k));); !标号约束(除起始点外); @for(link:@bin(x)); !0-1约束;@for(city(k)|k#gt#1:u(k)<=n-(n-2)*x(1,k); !起点标号约束;u(k)>=1+(n-1)*x(k,1);); !终点标号约束;end例2 装备的合理配置问题设有M套不同型号的装备要配备给M个部队,由于各个部队的基础设施、训练特点等条件的差异,不同的装备在不同的部队所产生的效能是不同的,具体的数据如表1所示。
试问如何分配这批装备,保证每个部队都有一套设备,并且使总的效能最大?表1 装备在不同部队效能表A B C D E F G H I装备部队1 0.14 0.17 0.23 0.55 0.47 0.26 0.19 0.17 0.122 0.37 0.40 0.49 0.09 0.05 0.53 0.42 0.39 0.123 0.59 0.62 0.67 0.22 0.17 0.06 0.03 0.02 0.084 0.11 0.12 0.16 0.06 0.03 0.19 0.14 0.12 0.465 0.12 0.14 0.19 0.24 0.19 0.46 0.37 0.35 0.106 0.10 0.12 0.15 0.06 0.03 0.39 0.33 0.30 0.217 0.11 0.14 0.18 0.47 0.39 0.06 0.03 0.02 0.258 0.63 0.65 0.73 0.07 0.04 0.22 0.17 0.14 0.099 0.29 0.30 0.36 0.05 0.03 0.05 0.02 0.01 0.44解 由题意可以知道,这个问题是属于一标准指派问题,即属于组合优化的范畴,在这里我们来建立组合优化模型,并且相应的方法进行求解。
将各部队关于各种装备的效能(表1)数据用矩阵S 表示,即用99()ij S s ⨯=表示分配装备j 给部队i 产生的效能。
用99()ij X x ⨯=表示决策矩阵,为一个0-1矩阵,即1ij x =表示将装备j 分配给部队i ;0ij x =表示不将装备j 分配给部队i ,则此时可以建立如下的优化规划模型:9911max ij ij i i P x s ===∑∑1(1,2,,9)..1(1,2,,9)0,1(,1,2,,9)ij j V ij i Vij x i s t x j x i j ∈∈⎧==⎪⎪==⎨⎪⎪==⎩∑∑L L L (2) 模型(2)是一个0-1规划模型,可以用LINGO 软件求解,其程序如下:model : sets : army/1..9/; equi/1..9/;assign(army,equi):s,x; endsets data : s=0.14 0.17 0.23 0.55 0.47 0.26 0.19 0.17 0.12 0.37 0.40 0.49 0.09 0.05 0.53 0.42 0.39 0.12 0.59 0.62 0.67 0.22 0.17 0.06 0.03 0.02 0.08 0.11 0.12 0.16 0.06 0.03 0.19 0.14 0.12 0.46 0.12 0.14 0.19 0.24 0.19 0.46 0.37 0.35 0.10 0.10 0.12 0.15 0.06 0.03 0.39 0.33 0.30 0.21 0.11 0.14 0.18 0.47 0.39 0.06 0.03 0.02 0.25 0.63 0.65 0.73 0.07 0.04 0.22 0.17 0.14 0.09 0.29 0.30 0.36 0.05 0.03 0.05 0.02 0.01 0.44; enddatamax =@sum (assign:s*x);@for (army(i):@sum (equi(j):x(i,j))=1); @for (equi(j):@sum (army(i):x(i,j))=1); @for (assign:@bin (x)); end例3 网络的数据传输问题分组交换技术在计算机网络发挥着重要作用,从源节点到目的节点传送文件不再需要固定的一条“虚路径”,而是将文件分割为几个分组,再通过不同的路径传送到目的节点,目的节点在根据分组信息进行重组、还原文件。
分组交换技术具有文件传输时不需要始终占用一条线路,不怕单条线路掉线,多路传提高传输速率等优点。
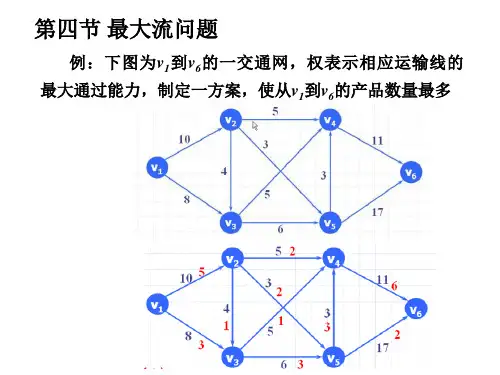
现在考虑如图2所示的网络,图中连接两个节点间的数字表示两交换机得可用宽带,此时从节点1到节点9的最大传输宽带是多少?解 将此问题视为一个求网络最大流问题,将分组的传输方式用以下矩阵来刻画:111219212229919299f f f f f f F f f f ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦L L M M O M L其中ij f 表示从节点i 到节点j 的实际传输宽带。
记容量矩阵为2.5 5.6 6.17.13.6 3.44.97.42.47.25.73.8 5.34.53.8 6.77.40C ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦由此可以建立线性模型如下:max f V(1)(9)..0(1,9)0f ij ki fj V k V V i f f V i s t i F C ∈∈=⎧⎧⎪⎪-=-=⎪⎨⎨⎪≠⎩⎪⎪≤≤⎩∑∑ (3)例4 出租车的最短行驶路线问题某市的出租车公司为了更好地为乘客服务,向乘客承诺:“出租车走最短的行驶路线,方便快捷。
”乘客上车后只要告知司机目的地,出租车上电脑就可以计算出到达目的地最短的行驶路线。
解 首先将地图视为一个赋权图。
function [d,DD]=dijkstra(D,s)%Dijkstra 最短路算法Matlab 程序用于求从起始点s 到其它各点的最短路 %D 为赋权邻接矩阵%d为s到其它各点最短路径的长度%DD记载了最短路径生成树[m,n]=size(D);d=inf.*ones(1,m);d(1,s)=0;dd=zeros(1,m);dd(1,s)=1;y=s;DD=zeros(m,m);DD(y,y)=1;counter=1;while length(find(dd==1))<mfor i=1:mif dd(i)==0d(i)=min(d(i),d(y)+D(y,i));endendddd=inf;for i=1:mif dd(i)==0&&d(i)<dddddd=d(i);endendyy=find(d==ddd);counter=counter+1;DD(y,yy(1,1))=counter;DD(yy(1,1),y)=counter;y=yy(1,1);dd(1,y)=1;end。