下载文档原格式
思考题参考答案第1章压力容器导言思考题1.1我国《压力容器安全技术监察规程》根据整体危害水平对压力容器进行分类。
压力容器破裂爆炸时产生的危害愈大，对压力容器的设计、制造、检验、使用和管理的要求也愈高。
设计压力容器时，依据化学介质的最高容许浓度，我国将化学介质分为极度危害（Ⅰ级）、高度危害（Ⅱ级）、中度危害（Ⅲ级）、轻度危害（Ⅳ级）等四个级别。
介质毒性程度愈高，压力容器爆炸或泄漏所造成的危害愈严重。
压力容器盛装的易燃介质主要指易燃气体或液化气体，盛装易燃介质的压力容器发生泄漏或爆炸时，往往会引起火灾或二次爆炸，造成更为严重的财产损失和人员伤亡。
因此，品种相同、压力与乘积大小相等的压力容器，其盛装介质的易燃特性和毒性程度愈高，则其潜在的危害也愈大，相应地，对其设计、制造、使用和管理也提出了更加严格的要求。
例如，Q235-B钢板不得用于制造毒性程度为极度或高度危害介质的压力容器；盛装毒性程度为极度或高度危害介质的压力容器制造时，碳素钢和低合金板应逐张进行超声检测，整体必须进行焊后热处理，容器上的A、B类焊接接头还应进行100％射线或超声检测，且液压试验合格后还应进行气密性试验。
而制造毒性程度为中度或轻度的容器，其要求要低得多。
又如，易燃介质压力容器的所有焊缝均应采用全熔透结构思考题1.2筒体：压力容器用以储存物料或完成化学反应所需要的主要压力空间，是压力容器的最主要的受压元件之一；封头：有效保证密封，节省材料和减少加工制造的工作量；密封装置：密封装置的可靠性很大程度上决定了压力容器能否正常、安全地运行；开孔与接管：在压力容器的筒体或者封头上开设各种大小的孔或者安装接管，以及安装压力表、液面计、安全阀、测温仪等接管开孔，是为了工艺要求和检修的需要。
支座：压力容器靠支座支承并固定在基础上。
安全附件：保证压力容器的安全使用和工艺过程的正常进行。
思考题1.3《压力容器安全技术监察规程》依据整体危害水平对压力容器进行分类，若压力容器发生事故时的危害性越高，则需要进行安全技术监督和管理的力度越大，对容器的设计、制造、检验、使用和管理的要求也越高。
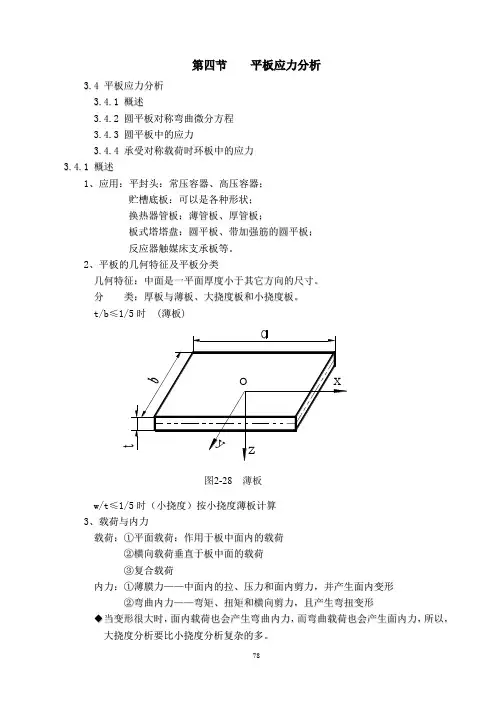
第四节平板应力分析3.4平板应力分析3.4.1概述3.4.2圆平板对称弯曲微分方程3.4.3圆平板中的应力3.4.4承受对称载荷时环板中的应力3.4.1概述1、应用：平封头：常压容器、高压容器；贮槽底板：可以是各种形状；换热器管板：薄管板、厚管板；板式塔塔盘：圆平板、带加强筋的圆平板；反应器触媒床支承板等。
2、平板的几何特征及平板分类w/t≤1/5时（小挠度）按小挠度薄板计算3、载荷与内力载荷：①平面载荷：作用于板中面内的载荷②横向载荷垂直于板中面的载荷③复合载荷内力：①薄膜力——中面内的拉、压力和面内剪力，并产生面内变形②弯曲内力——弯矩、扭矩和横向剪力，且产生弯扭变形◆当变形很大时，面内载荷也会产生弯曲内力，而弯曲载荷也会产生面内力，所以，大挠度分析要比小挠度分析复杂的多。
◆本书仅讨论弹性薄板的小挠度理论。
4、弹性薄板的小挠度理论基本假设---克希霍夫K i r c h h o f f① 板弯曲时其中面保持中性，即板中面内各点无伸缩和剪切变形，只有沿中面法线w 的挠度。
只有横向力载荷 ②变形前位于中面法线上的各点，变形后仍位于弹性曲面的同一法线上，且法线上各点间的距离不变。
类同于梁的平面假设:变形前原为平面的梁的横截面变形后仍保持为平面，且仍然垂直于变形后的梁轴线。
③平行于中面的各层材料互不挤压，即板内垂直于板面的正应力较小，可忽略不计。
◆研究: 弹性,薄板 / 受横向载荷 / 小挠度理论 / 近似双向弯曲问题3.4.2 圆平板对称弯曲微分方程分析模型分析模型：半径R ，厚度t 的圆平板受轴对称载荷P z ，在r 、θ、z 圆柱坐标系中，内力M r 、M θ、Q r 三个内力分量轴对称性：几何对称，载荷对称，约束对称，在r 、θ、z 圆柱坐标系中，挠度w 只是 r 的函数，而与θ无关。
求解思路：经一系列推导（基于平衡、几何、物理方程）→弯曲挠度微分方程（z p w ）→求w 求→内力r M M θ、→求应力r θσσ、微元体内力 ：径向：M r 、M r +（d M r /d r ）d r 周向：M θ、 M θ横向剪力：Q r 、Q r +（d Q r /d r ）d r 微元体外力 ：上表面z P p rd dr θ=2、几何协调方程(W ~ε)取AB dr =，径向截面上与中面相距为z ，半径为r 与r dr +两点A 与B 构成的微段板变形后：微段的径向应变为 ()r z d z d z dr dr ϕϕϕϕε+-==（第2假设）过A 点的周向应变为()222r z r z r rθπϕπϕεπ+-==（第1假设）作为小挠度dwdrϕ=-，带入以上两式，得 应变与挠度关系的几何方程：22r d wz dr z dw r drθεε=-=-（2-55） 3、物理方程根据第3个假设，圆平板弯曲后，其上任意一点均处于两向应力状态。
（1）承受均布载荷时圆平板中的应力板内剪力求解：如图，选取任意位置r 处的圆平板进行受力分析，建立轴向平衡式，可求得Q r22()2r r r r Q p rpr Q Q r ππ⋅=⋅==()r r Q Q r =注意：根据图2-29(c)来确定右图中剪力的符号。
将上述边界条件代入（2－63）式中，求得)µ+最大周向弯矩出现在板的中央处，而最大径向弯矩出现在板的边缘处。
此外，弯矩为负的含义表明其方向与当初规定的方向相反（见图2-29）。
类似于上述方法，可得到挠度方程板的上(负号)、下(正号)表面的应力分布如下()()()222222338(269)33(13)8r p R r t p R r t θσµσµµ⎧=+−⎪⎪−⎨⎪⎡⎤=+−+⎣⎦⎪⎩∓∓可见，板内最大拉应力在板的下表面中央部位处。
薄圆平板应力特点①板内为两向纯弯曲应力，忽略z 方向的应力σz 和剪力Q r 引起的剪应力τ。
②板内的弯曲应力沿径向的分布形式与周边支承形式有关，工程实际中的支承形式介于固支和简支之间。
③在同等条件下，板内的最大应力要远大于薄壳内的应力，故板的厚度要比薄壳厚度大。
（2）承受集中载荷时圆平板中的应力板内剪力求解：如图，选取任意位置r 处的圆平板进行受力分析，建立轴向平衡式，可求得Q r2()2r r r r Q PP Q Q r rππ⋅===()r r Q Q r =中心开有圆形孔的圆平板称为“环板”。
以周边简支，内周边承受均布力矩的环板分析为例。
122123()0102ln 4r r Q Q r d d dw r dr r dr dr C C dw r dr r C r w r C C R ϕ==⎡⎤⎛⎞=⎜⎟⎢⎥⎝⎠⎣⎦⎧=−=+⎪⎪⎨⎪=−−+⎪⎩2.3.4 承受轴对称载荷时环板中的应力如图所示环板，须注意与上述例子的不同在于，只是边界条件有所不同。
11,,00r r r R M M r R M and w ==−===Boundary Conditions:这样，我们就可以对许多类似的问题进行求解。
