2 第二讲 应力与应变解析
- 格式:ppt
- 大小:15.18 MB
- 文档页数:97

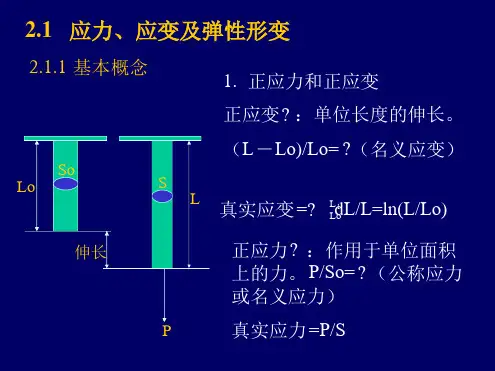


应变和应力的概念应变和应力的概念引言应变和应力是材料力学学科中的基本概念,它们是研究材料在受外部作用下的变形和破坏行为的重要参数。
本文将深入探讨应变和应力的概念、种类、计算及其在工程实践中的应用。
一、应变的概念1.1 定义应变是指物体在受外部作用下发生形状或大小上的改变程度。
通俗地说,就是物体发生了多少形变。
1.2 种类根据物体发生形变时,不同方向上长度或角度的改变情况,可分为以下几种类型:(1) 线性应变:也称伸长率,是指物体沿着外力作用方向上单位长度发生的相对伸长量。
(2) 非线性应变:也称剪切应变,是指物体内部各层之间因受到外部剪切力而产生相对滑动而引起角度改变。
(3) 体积应变:是指物体在三个互相垂直方向上同时发生尺寸改变所引起的相对体积改变量。
二、应力的概念2.1 定义应力是指物体在外部作用下,单位面积内所受的力。
通俗地说,就是物体受到了多大的力。
2.2 种类根据作用力的不同方向和大小,可分为以下几种类型:(1) 正应力:是指作用在物体上的力与该面积垂直的分量。
(2) 剪应力:是指作用在物体上的力与该面积平行的分量。
(3) 组合应力:是指同时存在正应力和剪应力时,在该面积上所受到的合成作用。
三、应变和应力之间的关系3.1 胡克定律胡克定律是描述弹性材料之间应变和应力之间关系的基本定律。
它表明,当材料受到外部载荷时,其产生的弹性形变量与所施加载荷成正比。
即:σ=Eε其中,σ为材料所受内部单位面积上产生的正应力;E为杨氏模量,表示单位长度内所需施加的正应力;ε为材料所发生线性形变(伸长率)。
3.2 应变-位移关系式对于线弹性材料,在外部载荷不超过其屈服极限时,它的应变与位移之间的关系可以用以下式子表示:ε=δ/L其中,ε为物体的线性应变(伸长率);δ为物体所受外力引起的位移;L为物体的原始长度。
四、应变和应力在工程实践中的应用4.1 应变计应变计是一种用于测量材料应变量的仪器。
它可以通过测量材料在受外部载荷时发生形变的程度来推算出其所受到的应力大小。


应变和应力的概念一、引言应变和应力是材料力学中重要的概念,在工程和科学研究中有着广泛的应用。
应变是描述物体形变程度的物理量,而应力则是描述物体内部受力状态的物理量。
本文将详细介绍应变和应力的概念,并深入探讨两者之间的关系。
二、应变的概念2.1 应变的定义应变是描述物体形变程度的物理量,通常用符号ε表示。
应变可分为线性应变和非线性应变两种情况。
线性应变发生在物体受到小的力引起的形变情况下,其应变与受力成正比。
非线性应变则发生在物体受到大的力引起的形变情况下,其应变与受力不成正比。
2.2 应变的分类1.纵向应变2.横向应变3.剪切应变4.体积应变三、应力的概念3.1 应力的定义应力是描述物体内部受力状态的物理量,通常用符号σ表示。
应力分为正应力和剪应力两种情况。
正应力是指垂直于物体截面的力在单位面积上的分布情况,剪应力是指平行于物体截面的力在单位面积上的分布情况。
3.2 应力的分类1.纵向应力2.横向应力3.剪切应力4.欧拉应力四、应变与应力的关系应变与应力之间存在着密切的关系,可以由材料的应力-应变曲线来描述。
应力-应变曲线显示了材料在受力下的变形和应力的关系,以此来研究材料的力学性质。
4.1 弹性阶段在弹性阶段,材料受力后会发生一定程度的形变,但当去除外力时,材料可以恢复到原先的形状。
此时应力与应变呈线性关系,称为胡克定律。
4.2 屈服阶段当外力超过了材料的弹性极限时,材料会进入屈服阶段。
此时材料会产生更大的形变,但仍能回复到非常接近原来形状的状态。
4.3 塑性阶段当外力超过了材料的屈服极限时,材料将进入塑性阶段,并发生不可逆的形变。
在这个阶段,应力与应变之间的关系不再是线性的,材料会呈现出时间依赖性和屈服后的流变行为。
4.4 断裂阶段当外力继续增加,超过了材料的断裂强度,材料将发生断裂并失去原有的结构完整性。
五、总结应变和应力是描述材料力学性质的重要概念。
应变是描述物体形变程度的物理量,而应力是描述物体内部受力状态的物理量。

应变和应力的关系公式应变和应力是力学中非常重要的概念,它们描述了物体在外力作用下的变形和反抗变形的能力。
应变是物体在外力作用下发生变形的程度,而应力是物体对外力的反抗程度。
应变和应力之间存在着一定的关系,下面将通过分析和解释来阐述这一关系。
我们来看一下应变的定义。
应变通常用来描述物体的形变程度。
当物体受到外力作用时,它的形状会发生改变,这种形变程度就是应变。
应变可以分为线性应变和非线性应变。
线性应变是指物体的形变与受力成正比,比如拉伸或压缩后物体的长度或体积的变化。
非线性应变则是指物体的形变与受力不成正比,比如物体的弯曲或扭转。
而应力则是物体对外力的反抗程度。
当物体受到外力作用时,它会产生内部的应力,以抵抗外力的作用。
应力可以分为正应力和剪应力。
正应力是指物体内部的应力沿着受力方向的成分,比如拉伸或压缩时物体内部的张力或压力。
剪应力则是指物体内部的应力与受力方向垂直的成分,比如物体发生弯曲或扭转时的切向应力。
应变和应力之间的关系可以通过胡克定律来描述。
胡克定律是力学中一个重要的定律,它描述了弹性体的应力和应变之间的线性关系。
根据胡克定律,当外力作用于弹性体时,弹性体产生的应变与外力成正比,且比例常数为弹性模量。
弹性模量是描述物体抵抗形变能力的物理量,通常用符号E表示。
胡克定律的数学表达式为:应力=弹性模量×应变。
这个关系可以简洁地表示了应变和应力之间的关系。
根据这个关系,我们可以推导出应变和应力之间的其他关系。
比如,如果已知应变和弹性模量,可以通过应变乘以弹性模量来计算应力。
同样地,如果已知应力和弹性模量,可以通过应力除以弹性模量来计算应变。
除了胡克定律,还有其他的应变与应力之间的关系,比如柯西应变与柯西应力之间的关系、拉梅应变与拉梅应力之间的关系等。
这些关系都是通过实验和理论推导得到的,它们描述了不同应变与应力之间的关系,适用于不同的物体和力学问题。
总结起来,应变和应力之间存在着一定的关系,可以通过胡克定律或其他相关定律来描述。

详解内力、应力、应变一、内力的概念1. 定义内力,是指由外力作用所引起的、物体内相邻部分之间相互作用力(附加内力)。
杆件所受到外界施加的力称为外力。
如图所示为任意一个物体,它是由无穷多的微粒组成的,构件内任意相邻两个微粒之间存在着相互作用力,作用力的大小与微粒之间的相对位置有关系。
当物体受到外力作用后,物体发生变形,其内部微粒之间的相对位置发生改变,它们之间的相互作用力随之发生改变。
我们把这个由外力作用而产生的作用力的改变量称为附加内力,简称为内力。
2. 内力的求法——截面法显然内力在构件的内部,想要求解内力,只有让内力暴露出来,这样根据需要求解内力的截面位置,我们采用截面法。
假想地把该截面截开,原构件是平衡的,截开后的任意一部分也是平衡的,即截面两侧的任意一部分在外力及截面上的内力作用下处于平衡状态。
因此,可以取截面的任意一侧,研究其平衡条件,建立平衡方程,求解该截面上的内力。
具体截面求解步骤如下。
•假想截开:在所求内力的截面处(一般是横截面),假想地用截面将杆件一分为二。
••代替:任意取一部分,其舍弃部分对留下部分的作用,用作用在截面上相应的内力(力或力偶)代替。
•平衡:对留下的部分建立平衡方程,根据其上已知外力来计算杆在截开面上的未知内力(此时,截开面上的内力对所保留部分而言是外力)。
根据均匀性连续性的基本假设,截开后的截面上应该是连续分布着一任意力,截面上各点处都有内力,而空间任意力系的平衡条件只有六个,我们求解不出所有各点的内力。
根据力系的简化,我们把这个内力的任意力系向截面的一点简化,通常向截面的形心简化,得到一个主矢一个主矩,如下图所示。
以截面形心为原点,建立直角坐标系如图x轴垂直于横截面,即沿杆的轴线方向,y、z轴在截面面内。
把主矢向三个坐标轴分解可得三个分量:沿着x轴的轴力,沿着y轴和z轴的剪力。
把主矩向三个坐标轴分解可得三个分量:沿着x轴的扭矩,沿着y轴和z 轴的弯矩。
我们把这六个分量也称为内力,但是要注意这六个分量是内力的合力或合力矩。
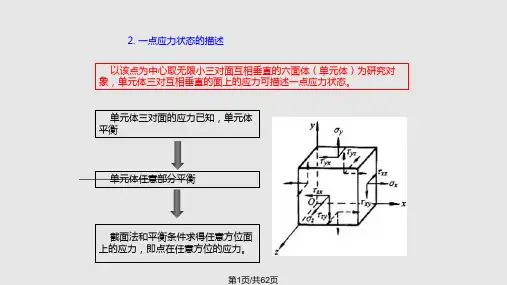

应力和应变分析应力和应变分析是材料力学中非常重要的一项内容,它们研究材料在外力作用下的变形行为。
应力是表征材料单位面积内的力的大小,而应变则是描述材料单位长度内的变形程度。
应力和应变的分析可以帮助我们理解材料的强度和刚度,以及材料在不同条件下的变形和破坏机制。
本文将从应力和应变的定义、材料的本构关系和应变测量等方面进行探讨。
首先,应力的定义为单位面积内的力的大小,常用符号为σ,其计算公式为σ=F/A,其中F为施加力的大小,A为力作用的面积。
应力的单位通常为帕斯卡(Pa),1Pa等于1N/m^2、根据作用力的不同方向,应力又可以分为正应力和剪应力。
正应力是垂直于材料截面的力,剪应力则是在材料截面上平行于切平面的力。
其次,应变是材料受力后发生的形变程度,常用符号为ε,其计算公式为ε=ΔL/L0,其中ΔL为长度的增量,L0为力作用前的长度。
应变的单位为无量纲。
类似于应力,应变也有正应变和剪应变之分。
正应变是材料在力作用下产生的沿体积方向的变化,剪应变则是在截面上平行于剪切力方向的变化。
应力和应变之间的关系可以通过材料的本构关系来描述。
材料的本构关系是材料在应力与应变之间的函数关系,通常以应力-应变曲线的形式表示。
根据材料的性质不同,应力-应变曲线可以分为线性区、弹性区、屈服区、塑性区和断裂区。
在线性区内,应力和应变呈线性关系,材料具有良好的弹性行为。
在弹性区内,材料回复到原始形状,没有永久性变形。
当应力超过一定的值时,材料进入屈服区,出现塑性变形。
塑性区内,材料的应变增大,但没有太大的应力增加。
当材料无法再承受应力引起继续塑性变形时,出现断裂。
最后,应变的测量是应力和应变分析的重要一环。
常用的应变测量方法包括拉伸试验、剪切试验、压缩试验等。
拉伸试验是最常见的应变测量方法之一,通过施加拉力来测量材料在不同应力下的应变。
剪切试验则是通过施加剪切力来测量材料的剪切应变。
压缩试验则是将材料压缩后测量其压缩应变。

工程力学中的应变与应力分析工程力学是研究物体静力学和动力学的一门学科,它在工程设计和结构力学分析中起着重要的作用。
在工程力学中,应变与应力是两个基本概念,也是进行结构分析和材料力学计算的关键参数。
本文将从应变和应力的定义、计算公式、应变与应力的关系等方面进行介绍与分析。
一、应变的概念与计算应变是物体在受到力的作用下,发生形变的程度的度量。
应变可分为线性应变和切变应变两种。
1. 线性应变线性应变是指物体在受力作用下,其形变呈现线性关系。
常见的线性应变有拉伸应变和压缩应变。
拉伸应变是指物体在拉伸力作用下的伸长变化程度,压缩应变是指物体在压缩力作用下的压缩变化程度。
线性应变的计算公式如下:ε = ΔL / L其中,ε表示线性应变,ΔL表示长度变化量,L表示物体的初始长度。
2. 切变应变切变应变是指物体在受到剪切力作用下,产生的剪切变形程度。
切变应变的计算公式如下:γ = θ * r其中,γ表示切变应变,θ表示切变角度,r表示物体上两点间的距离。
二、应力的概念与计算应力是物体内部受力作用下单位面积上的力的大小。
常见的应力有拉应力、压应力和剪应力等。
应力的计算公式如下:1. 拉应力和压应力拉应力是指垂直于物体横截面的拉力作用下,单位面积上的力的大小,压应力是指垂直于物体横截面的压力作用下,单位面积上的力的大小。
拉应力和压应力的计算公式如下:σ = F / A其中,σ表示应力,F表示作用力的大小,A表示物体的横截面积。
2. 剪应力剪应力是指平行于物体横截面的剪切力作用下,单位面积上的力的大小。
剪应力的计算公式如下:τ = F / A其中,τ表示剪应力,F表示作用力的大小,A表示物体的横截面积。
三、应变与应力的关系应变与应力有着密切的关系,可以通过应变与应力的计算公式来解析他们之间的关系。
1. 杨氏模量杨氏模量是一种材料的特性参数,它是应力与应变之间的比值。
杨氏模量的计算公式如下:E = σ / ε其中,E表示杨氏模量,σ表示应力,ε表示应变。
应力和应变1. 简介在力学和材料科学中,应力和应变是两个重要的概念。
应力是指材料内部受到的力的作用,而应变是指材料在受到力作用后发生的形变。
应力和应变是描述材料力学性能的基本参数,对于材料的设计和工程应用具有重要意义。
2. 应力应力是材料内部受到的力的作用,通常用符号σ表示,其单位是帕斯卡(Pa),也可以使用兆帕(MPa)或千兆帕(GPa)。
应力可以分为三类:正应力、剪应力和法向应力。
2.1 正应力正应力是指作用在材料内部的垂直于截面的力,可以通过力除以截面积来计算。
正应力可以进一步分为拉应力和压应力,分别表示拉伸和压缩材料时的应力。
拉应力表示材料受到拉伸作用时的应力,通常以正数表示。
拉应力会使材料发生形变,具有延展性和弹性,可以恢复原状。
压应力表示材料受到压缩作用时的应力,通常以负数表示。
压应力会使材料发生形变,具有收缩性和塑性,并且不易恢复原状。
2.2 剪应力剪应力是指作用在材料内部的平行于截面但方向不同的力,可以通过力除以截面积来计算。
剪应力会使材料发生扭转和剪切形变。
剪应力会产生剪切变形,对应的是材料的剪切模量,可以用于描述材料的硬度和可塑性。
2.3 法向应力法向应力是指作用在材料内部的垂直于截面方向的力,可以通过力除以截面积来计算。
法向应力会使材料发生压缩或拉伸形变。
法向应力的大小和方向取决于施加力的方向和大小,可用于描述材料的稳定性和破坏性。
3. 应变应变是材料在受到力作用后发生的形变,通常用符号ε表示。
应变可以分为线性应变和非线性应变两类。
3.1 线性应变线性应变是指材料在受到小应力作用时,形变与力之间的关系是线性的。
线性应变可以通过材料的弹性模量来描述,弹性模量是材料在小应力作用下恢复原状能力的度量。
3.2 非线性应变非线性应变是指材料在受到大应力作用时,形变与力之间的关系是非线性的。
非线性应变通常发生在超过材料弹性极限时,即材料开始变形并难以恢复原状的阶段。
非线性应变可以引起材料的塑性变形和破坏,对于材料的设计和使用具有重要影响。
第二章应力和应变地震波传播的任何定量的描述,都要求其能表述固体介质的内力和变形的特征。
现在我们对后面几章所需要的应力、应变理论的有关部分作简要的复习。
虽然我们把这章作为独立的分析,但不对许多方程进行推导,读者想进一步了解其细节,可查阅连续介质力学的教科书。
三维介质的变形称为应变,介质不同部分之间的内力称为应力。
应力和应变不是独立存在的,它们通过描述弹性固体性质的本构关系相联系。
2.1 应力的表述——应力张量2.1.1应力表示考虑一个在静力平衡状态下,均匀弹性介质里一个任意取向的无限小平面。
平面的取向可以用这个平面的单位法向矢量nˆ来规定。
在nˆ方向的一侧施加在此面单位面积上的力叫做牵引力,用矢量),,()ˆ(zyxtttnt=表示。
在nˆ相反方向的另一侧施加在此面上的力与其大小相等,方向相反,即)ˆ()ˆ(ntnt-=-。
t在垂直于平面方向的分量叫做法应力,平行于平面方向的分量叫做剪应力。
在流体的情况下,没有剪应力,nptˆ-=,这里P 是压强。
上面的表示这是一个平面上的应力状况,为表示固体内部任意平面上的应力状态,应力张量τ在笛卡尔坐标系(图 2.1)里可以用作用于xyxzyz,,平面的牵引力来定义(:ˆˆˆ()()()ˆˆˆ()()()ˆˆˆ()()()xx xy xzx x xy y y yx yy yzz z z zx zy zzt x t y t zt x t y t zt x t y t zττττττττττ⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦(2.1)在右式的表示中,第一个下角标表示面的法线方向,第二个下角标表示该面上应力在该坐标轴上的投影。
图2.1 在笛卡尔坐标系里描述作用在无限小立方体面上的力的牵引力矢量)ˆ(),ˆ(),ˆ(z t y t xt 。
应力分量的符号规定如下:对于正应力,我们规定拉应力为正,压应力为负。
对于剪应力,如果截面的外法线方向与坐标轴一致,则沿着坐标轴的正方向为正,反之为负;如果截面方向与外法线方向相反,则沿着坐标轴反方向为正。