当前位置：文档之家 › 信息光学第5

信息光学第5

  • 格式：ppt
  • 大小：16.46 MB
  • 文档页数：131

下载文档原格式

  / 131

合集下载

信息光学(傅里叶光学)Chap5-2

信息光学(傅里叶光学)Chap5-2

成像系统的普遍模型——黑箱模型
复习：（几何光学） 复杂光学系统由多个透镜（正、负、厚、薄不同） 和光阑组成。透镜孔径也构成光阑。 光阑：光学元件的边框和特加的有一定形状开孔的屏统称 光阑。有拦光作用（对成像光束的大小有限制作用）。
#
§5-2 成像系统的一般分析
成像系统的普遍模型——黑箱模型
孔径光阑（孔阑 Aperture Stop）：所有光阑中有一个 对成像光束最终起到实际限制的作用，决定成像光 束截面或立体角，称为孔径光阑。（注意不一定几 何尺寸最小） 入射光瞳（入瞳 Entrance Pupil）：孔径光阑通过它前 面的光具组所成的像。由于物像共轭关系，物方能 通过入瞳的光束，必定能完全通过孔阑。 出射光瞳（出瞳 Exit Pupil）：孔径光阑通过它后面 的光具组所成的像。 所以，通过孔阑的光束在像方能完全通过出瞳。 #
衍射受限系统的脉冲响应是光学系统出瞳的夫琅和费衍射 图样.中心在几何光学理想像点 任意复杂的衍射受限光学成像系统，都可看作线性空不变系统. 像的复振幅分布是几何光学理想像和系统出瞳所确定的脉冲响 应的卷积。 #
§5-2 成像系统的一般分析 四、非单色照明
光学系统的成像性质与照明方式有密切的关系
实际光源不是严格单色，总有一定的光谱线宽Δ n. 本节讨论准单色照明, 即Δ n << n, n是照明光波的平均频率。 在非单色光照明的情况下，光场扰动可表示为

T
2
Hale Waihona Puke T 2U i xi , yi ; t U i xi , yi ; t dt


T
2
T
2
dt U 0 x0 , y0 ; t h( xi , yi ; x0 , y0 )dx0 dy0

信息光学PPT课件第五章光学全息

信息光学PPT课件第五章光学全息

)
Uc (x,
y, z)
Ae jkr
U
( x,
y,
z)
U( x, y, z) Ae jkr Aexp jk( x cos y cos z cos )
Uc ( x, y, z) Ae jkr U ( x, y, z)
共轭光波的数学表达式为原光波复振幅的共轭复数。
已知 于是
参考波
R
记录介质上的的总光强为 I( x, y) O( x, y) R( x, y) 2
O
物波
记录介质
O( x, y) 2 R( x, y) 2 R( x, y)O( x, y) R( x, y)O( x, y)
O(x, y) 2 R(x, y) 2 2r(x, y)O0(x, y)cos (x, y) (x, y)
参考波
R
O
物波
记录介质
上图为波前记录的示意图,设传播到记录介质上的物光波前复振幅（对于理 想单色光，其空间的复振幅分布是不随时间变化的）为
O( x, y) Oo ( x, y)exp j ( x, y)
传播到记录介质上的参考光波前复振幅
R( x, y) r( x, y)exp j ( x, y)
全息图片
全息图片
当照明光波与参考光波均为正入射的平面波时，入射到 全息上的相位可取为零。这时U3和U4中的系数均为实 数，无附加相位因子，全息图衍射场中的+1级和-1级光 波严格镜像对称。由共轭光波U4所产生的实像，对观察 者而言，该实像的凹凸与原物体正好相反，因而给人以 某种特殊的感觉，这种像称为赝像。
如何得到三维的图像呢？
如果我们能够用某一种方法把物体光波（其中包含振幅和 相位信息）以某种方式记录下来，则当我们想办法把物光波 再现出来的话，就能再现三维的物体。

信息光学第5

信息光学第5

12 年后激光器问世，第一台红宝石激光器 诞生，解决了相干光源的问题。
英国伦敦帝国大学工作

接着E.Leith和J.Upatnieks就用激 光拍摄成了完善的全息照片，在 一张平面全息图底片的后面重现 出原物逼真的三维形象，令人赞 叹不已。
视差效应
立体电影就是用两个镜头如人眼那样的拍摄装置，拍摄下景物的双视点

干涉图记录到记录介质上形成全息图
全息记录介质有多种。常用的是涂有卤化银乳胶的银盐感光板（或胶片）。 经适当显影、定影等处理后，就得到全息图。
全息干板（胶片）的结构：
感光层：银盐乳胶，由照相明胶、卤化银颗粒、及适量的补 加剂（包括坚膜剂、增感剂、稳定剂等）组成。明胶不仅是 感光层的成膜物质，而且具有很好的分散作用，使超微粒的 卤化银晶粒(0.03um-0.08um)能均匀分散其中。
2 2
2O R I r , t R O 1 2 cos R r O r 2 R O
2 2


条纹对比度： V
2O R O R
2 2
条纹形状由位相差 φR-φO 决定。因此，全息图片经曝光、显 影、定影等处理后，不仅记录了关于两光波的强度信息，也记录了 他们的振幅和位相信息。可以想象，φR-φO的空间变化不一定是线 性的，也不一定是单调的，因而干涉条纹的疏密、取向、强弱和对 比度都是在随处变化。但其变化不是随机的，而是以 φR随空间较 规则的变化为标准，把物光波的位相分布φO以光强度变化的形式 反应出来，而振幅则以条纹的调制深度被记录下来。
显微镜下观察的干涉条纹。 从空间频率上说，大概每 毫米分布上千条条纹—— 与光路布置有关。

全息图的记录和重现
扩束镜

信息光学第五章解读

信息光学第五章解读

实际操作怎样记录物体的干涉信息？ • 常用的记录介质是银盐感光胶片，对两个波前的干涉图样
曝光后，经显影处理得到全息图。 • 记录介质的作用相当于线性变换器，它把曝光时的入射光
强线性地变换为显影后的振幅透过率分布。 • 全息图振幅透过率与光强成正比：
x, y 0 I x, y
为常数，与底片曝光和显影过程有关，
光学全息
主讲人：徐世祥
教学内容
光学全息基本原理 同轴和离轴全息图 基元全息图 傅立叶变换全息图 体积全息、计算全息 全息术的应用
教学目的和要求
本章是信息光学的应用，重点是全息术的基本原理，傅立叶 变换全息；要求学生掌握基本原理，实现各种全息图的方法 及其特点.
概述
• 普通感光片:只能记录光波的振幅(光强)，不能记录相位， 不能真实地重现原来的物光波，图像缺乏立体感。
• 成像具有三维特性，可以从不同的角度观测，而几何成像是 平面像；
• 成像的方式不同：几何成像记录物面上的相对光强分布，而 全息成像记录物体光波，包含相位信息。
• 全息图具有弥散性：一张用激光重现的透射式全息图，即使 被打碎成若干小碎片，用其中任何一个小碎片仍可重现出所 拍摄物体的完整的形象。不过当碎片太小时，重现景像的亮 度和分辨率会伴随着降低。 而几何成像，去掉一部分底片，就去掉一部分像。
量。I(x,y) t （光强时间）
强度透过率：透过光强/入射光强。 e2h
光密度：表示显影、定影后底片上单位面积的含银量。它 与强度透过率倒数的对数成正比。
CCD记录：数值再现。
三、全息图记录和再现小结
• 波前记录：光的干涉效应，它使振幅和位相调制的信息变 换为干涉图的强度调制信息，相对于一“编码”过程；
• 全息术是基于光的干涉和衍射现象，系统就应满足一定的相 干要求： 1）激光具有足够的时间相干性和空间相干性； 2）记录介质具有足够的分辨率，与物光可参考光的夹角相 适应； 3）曝光期间，光学系统应稳定到波长的十分之一以内； 4）物光、参考光的强度比例要适当。

信息光学(傅里叶光学)Chap5-3

信息光学(傅里叶光学)Chap5-3


~ h xi , yi exp j 2 f x x f y y dxi dyi


(h = h/M)
C M c M c M



2 xi yi dd exp j 2 f x x f y y dxi dy P , exp j d i
-1
0
1
2
我们仍可不考虑高频振荡部分，而仅考虑其复振幅U (x,y,t), 它既是空间函数又是时间函数, 随时间缓慢变化,可看成频率 为 的单色光波的包络。
#
§5-2 成像系统的一般分析 四、非单色照明
在同一时刻t,像的复振幅与物的复振幅之间应满足叠加积分：
U i xi , yi , t U 0 x0 , y0 ; t h xi , yi ; x0 , y0 dx0 dy0

2


1 lim t T T


T
T 2
U 0 x0 , y0 ; t U 0 * x0 ' , y0 ' ; t dt
dx0 dy0 dx0 ' dy0 ' h( xi , yi ; x0 , y0 )h * ( xi , yi ; x0 ' , y0 ' ) U 0 x0 , y0 ; t U 0 * x0 ' , y0 ' ; t
筛选性质(乘积积分性质): x, y x x0 , y y0 dxdy x0 , y0
Hc fx, f y


取反射坐标系: (对称光瞳自然成立)
P , d i f x , d i f y dd P d i f x ,d i f y P d i f x , d i f y

信息光学_第五章第三讲

信息光学_第五章第三讲

光瞳函数的总面积为
S0 l 2
当P（x,y）在 x方向和y方向分别位移 di f x , di f y , 以后 得 P( x di f x , y di f y ) 平移后的光瞳与原光瞳的重叠面积
S( fx , f y )
y
S( fx , f y )
di f y
x

~ H c ( f x , f y ) F{h ( xi , yi )}
~ h( x , y ) h ( xi , yi ) i i P(di ~ x , di ~ y ) exp j 2 [ xi ~ x yi ~ y ]d~ x d~ y |M |
三、OTF和CTF的关系
H f x , f y m f x , f y exp jφ
Ai ( f x , f y ) Ag ( f x , f y )
f , f
x y
m( f x , f y )
HI( fx ,f y ) H I ( ,)
i
称为调制传递函数（MTF）
称为相位传递函数（PTF）
0
di f x l d i f y l
(l d i f x )( l d i f y )
S( fx , f y )
di f x l d i f y l
其它
0
光学传递函数为
(l di f x )(l di f y ) d f l S( fx, f y ) i x 2 H( f x , f y ) l di f y l S0 0 其它
光学传递函数 H f x , f y 与相干传递函数 H c f x , f y 分 别 描 述 同一系统采用非相干和相干照明时的传递函数，它们都决定 于系统本身的物理性质，相互有联系。

傅立叶光学(信息光学)_课件

傅立叶光学(信息光学)_课件
1 x>0 Step（x）= ½ x=0
0 x<0
step(x)
1
0
step(x-x0),间断点移到x0处
x
二、符号函数：描述某孔径一半宽有 的位相差
1 x>0 Sgn（x）= 0 x=0
-1 x<0
Sgn(x)=2step(x)-1
sgn(x)
1
x
0
1
三、矩形函数（门函数）：表示狭缝、矩孔的透过
傅立叶光学
第一章 绪论 第二章 线性系统与Fourier分析 第三章 光波的标量衍射理论 第四章 透镜的Fourier变换性质 第五章 光学成像系统的频率响应 第七章 光学全息 第八章 空间滤波与光学信息处理
第一章 绪论
一、“信息光学”的含义 信息光学＝数学工具（级数、积分）＋经典光学 （光波的传播、干涉、衍射、成像、光学信息的记 录与再现、光学信号的处理）
2、光学中的线性叠加原理uv uuv uuv 波的迭加原理：矢量：E E1( p) E2( p) L
n
相干光场：复振幅：U（p）=Ui ( p) i 1
n
非相干光场：光强：I ( p) Ii ( p) i 1
3、利用系统的特性来求输入/输出关系 “三步法则”： 第一步：将复杂输入分解为简单输入函数之和 第二步：分别求出简单函数的输出 第三步：将简单函数输出加起来
2.1 线性系统的基本概念 一、系统：同类事物按一定关系所组
成的整体
特征(性)：不管内部结构，只是全体与外 部的关系，是整体行为，综 合行为
二、物理系统：由一个或多个物理装
置所组成的系统
1、概念：考虑与外形的信息交换 2、内容：输入/输出关系 3、特点：系统的外特性 4、作用：对输入信号变换作用——运算作用

《信息光学》教学大纲

《信息光学》教学大纲

《信息光学》课程教学大纲一、课程基本信息二、课程简介信息光学是应用光学、计算机和信息科学相结合而发展起来的一门新的光学学科，是信息科学的一个重要组成部分，也是现代光学的核心。

本课程主要介绍信息光学的基础理论及相关的应用，内容涉及二维傅里叶分析、标量衍射理论、光学成像系统的频率特性、部分相干理论、光学全息照相、空间滤波、相干光学处理、非相干光学处理、信息光学在计量学和光通信中的应用等。

三、课程目标本课程是光电信息科学与工程专业的主要专业课程之一，设置本课程的目的是让学生掌握信息光学的基本概念、基础理论及光信息处理的基本方法，了解光信息处理的发展近况和运用前景。

为今后从事光信息方面的生产，科研和教学工作打下基础。

四、教学内容及要求第一章信息光学概述（2学时）1.信息光学的基本内容和发展方向2.光波的数学描述和基本概念3.相干光和非相干光4.从信息论看光波的衍射要求：1.了解信息光学的内容和发展方向2.掌握相干光和非相干光的特点3.掌握从信息论的观点看光波的衍射。

重点：空间频率，等相位面。

从信息光学看衍射的基本观点。

难点：空间频率，光波的数学描述。

第二章二维傅里叶分析（8+2学时）1．光学常用的几种非初等函数2．卷积与相关3．傅里叶变换的基本概念4．线性系统分析5．二维采样定理要求：1．了解光学中常用非初等函数的定义、性质，熟悉它们的图像及在光学中的作用2．了解卷积与相关的定义及基本性质3．熟悉傅里叶变换的基本原理，性质和几何意义4．熟悉系统的基本概念及线性系统分析的基本理论5．了解二维采样定理及其应用6．本章强调概念的物理意义理解，以定性和应用为主。

避免与《信号与系统》课程重复。

重点：δ函数的意义和运算特性，傅里叶变换性质、定理，相关和卷积的意义及运算，线性空间不变系统的特性。

难点：卷积，傅里叶变换、系统分析。

第三章标量衍射理论（6+2学时）1．基尔霍夫衍射理论2．菲涅耳衍射和夫琅和费衍射3．夫琅和费衍射计算实例4．菲涅尔衍射计算实例5．衍射的巴俾涅原理要求：1．了解基尔霍夫衍射理论2．熟悉菲涅耳- 基尔霍夫衍射公式及其物理意义3．熟悉菲涅耳衍射与夫琅和费衍射4．掌握常见夫琅和费衍射光场的分析与计算5．了解菲涅耳衍射光场的分析和计算6．了解巴俾涅原理及其应用重点：如何用二维傅里叶变换来分析和计算夫琅和费衍射。

信息光学 第五章 光学全息

信息光学 第五章 光学全息


有



式中：第一项是 函数，表示直接透射光经透镜会 聚在像面中心产生的亮点；第二项是物分布的自相关 函数，形成焦点附近的一种晕轮光；第三项是原始像 的复振幅，中心位于反射坐标系的（0，b）处；第四 项是共轭像的复振幅，中心位于反射坐标系的（0，-b） 处，第三、四项都是实像。 设物体在y方向上的宽度为 ，则第二项自相关函数 y 的宽度为 ，原始像和共轭像的宽度均为 ，故要 y 2 y 3 使再现像不受晕轮光的影响，必须使 。 b y 2 安排光路时应保证这一条件。

p p p

注意到 ，说明再现的两个像点位于通过 xi / yi x p / y p 全息图原点的倾斜直线上。这表明，即使用轴外照明 光源再现，同轴全息图产生的各分量衍射波仍然沿同 一方向传播，观察是互相干扰。图5.5.2给出了电源同 轴全息图再现的情况。
5.6 傅立叶变换全息图

物体的信息由物光波所携带，全息记录了物 光波，也就记录下了物体所包含的信息。物 体信号可以在空域中表示，也可以在频率中 表示，也就是说，物体或图象的光信息既表 现在它的物体光波中，也蕴含在它的空间频 谱内。因此，用全息方法既可以在空域中记 录物光波，也可以在频域中记录物频谱。物 体或图象频谱的全息记录，称为傅立叶变换 全息图。

5.6.2 准傅立叶变换全息图

在图5.6.3所示的光路中，平行光垂直照射物体，透镜 紧靠物体放置，参考点源与物体位于同一平面上，在 透镜后焦面处放置记录介质。

根据透镜的傅立叶变换性质，则全息图平面上的物光 分布为
式中， ， 是物函数 的 x / f , y / f G( , ) g x0 , y0 傅立叶变换。 注意：由于该项前面出现的二次相位因子，是物体的 频谱产生了一个相位弯曲，因而全息图平面上的物光 波并不是物体准确的傅立叶变换。 设参考点位于（0，-b）处，参考点源的表达式为

信息光学第五章苏显渝版作者窦柳明

信息光学第五章苏显渝版作者窦柳明
记录介质表面的总光场分布为：
R( x, y) O( x, y)
A
O
B
D
C
R
记录介质表面的光强分布：
I(x, y) O(x, y) R(x, y) O(x, y) R(x, y)
5.2 波前记录与再现
I(x, y) O(x, y) R(x, y) O(x, y) R(x, y)
全息：全部信息，振幅和相位。 以上这种记录和再现物光波的技术叫全息照相术（全息术）。
全息的波前记录和再现过程就是调制与解调的过程。其中参考 光波是载波，物光波是调制光波，干涉记录过程就是调制，衍 射再现就是解调。
5.1 光学全息概述
5.1.2 光全息发展历史概述
一、全息术的提出：
是由丹尼斯·盖伯（Dennis Gabor）发明的。1947年，他从事电 子显微镜研究工作，当时由于电子透镜的像差，使电子显微镜分辨 率的提高碰到了很大的困难，（理论分辨极限是0.4nm，而实际只能 达到1.2nm）。盖伯从布喇格（Bragg）的X射线衍射显微镜中受到 启发，设想不用任何透镜，用经物体衍射的电子波与相干的背景波 重叠，将物体衍射波的振幅和相位以干涉条纹的形式记录在照相底 片上（他首次称之为全息图），然后用波长比电子波波长大105倍的
tH ( x, y) tb ( O 2 RO RO )
用一束相干光波作为再现光波照射全息图，它在全息图平面 前的光场分布为C(x,y)，则透过全息图的光场分布为：
U ( x, y) C( x, y)tH ( x, y) tbC OOC RCO RCO U1 U2 U3 U4
U1 ：系数的作用仅仅改变照明光波C的振幅，并不改变C的特性。

中山大学信息光学习题课后答案--习题4 5 6作业资料

中山大学信息光学习题课后答案--习题4 5 6作业资料

中山大学信息光学习题课后答案--习题456作业习 题 44.1 尺寸为a b ⨯的不透明矩形屏被单位振幅的单色平面波垂直照明，求出紧靠零后的平面上透射光场的角谱。

4.2 采用单位振幅的单色平面波垂直照明具有下述透过率函数的孔径，求菲涅耳衍射图样在孔径轴上的强度分布：(1) 220000(,)circ()t x y x y =+ (2) 2200001,1(,)0,a x y t x y ⎧⎪≤+≤=⎨⎪⎩其它 4.3 余弦型振幅光栅的复振幅透过率为：00()cos(2/)t x a b x d π=+式中，d 为光栅的周期，0a b >>。

观察平面与光栅相距z 。

当z 分别取下述值时，确定单色平面波垂直照明光栅，在观察平面上产生的强度分布。

(1) 22r d z z λ== (2) 22r z d z λ== (3) 242r z d z λ== 式中：r z 为泰伯距离。

4.4 参看下图，用向P 点会聚的单色球面波照明孔径∑。

P 点位于孔径后面距离为z 的观察平面上，坐标为(0,)b 。

假定观察平面相对孔径的位置是在菲涅耳区内，证明观察平面上强度分布是以P 点为中心的孔径的夫琅禾费衍射图样。

4.5 方向余弦为cos ,cos αβ，振幅为A 的倾斜单色平面波照明一个半径为a 的圆孔。

观察平面位于夫琅禾费区，与孔径相距为z 。

求衍射图样的强度分布。

4.6 环形孔径的外径为2a ，内径为2a ε(01)ε<<。

其透射率可以表示为：001,()0,a r a t r ε≤≤⎧=⎨⎩其他用单位振幅的单色平面波垂直照明孔径，求距离为z 的观察屏上夫琅禾费衍射图样的强度分布。

4.7 下图所示孔径由两个相同的圆孔构成。

它们的半径都为a ，中心距离为d ()d a >>。

采用单位振幅的单色平面波垂直照明孔径，求出相距孔径为z 的观察平面上夫琅禾费衍射图样的强度分布并画出沿y 方向截面图。

【信息光学课件】第五章光学全息2 PDF版

【信息光学课件】第五章光学全息2 PDF版
−∞ ∞
[
]
= R0 exp( j 2πf x b )
iii) 得光强为：
∗ ~ ~∗ I = O ( f x f y ) + R( f x f y ) ⋅ O ( f x f y ) + R( f x f y )
[
][
]
]
∗ 2 O ( f x f y ) + R0 + R0O ( f x f y ) ⋅ exp [ − j 2π f x b ] + R0O ( f x f y ) ⋅ exp [ − j 2π f x b ]
在象面上取反射坐标，经傅里叶变换有，

第一项：
~∗ ~ ~* ~ ℑ O (ξ ,η ) ⋅ O (ξ ,η ) = O ( x, y ) ★ O ( x ′, y ′)
−1
[
]

第二项： ℑ
−1
(R ) = R δ (x′, y ′)
2 0 2 0
---------自相关函数

-------- δ 函数 −1 (ξ ,η ) ⋅ exp ( − j 2πξ b ) O 第三项： ℑ
(
)
⋅ exp( j 2πξb ) ⋅

在记录面上的光强为：
2 ~ ~ I = U ( x, y ) + R ( x, y )
(ξ ,η ) ⋅ exp ( − j 2πξ b ) * + R2 + c ′ = UU R O 0 0
* (ξ ,η ) ⋅ exp ( j 2πξ b ) ′R0O +c
5.6傅里叶变换全息图 物体的信息由物光波所携带，全息记录了物 光波，也就记录了物体所携带的信息。物体 信号可以在空域中表示，也可以在频域中表 示，也就是说物体或图像的光信息既表现在 它的物体光波中，也蕴含在它的空间频谱内， 因此用全息法即可以在空域中记录物光波， 也可以在频域中记录物频谱。物体或频谱的 全息记录，称为傅里叶变换全息图。

信息光学智慧树知到课后章节答案2023年下北京工业大学

信息光学智慧树知到课后章节答案2023年下北京工业大学

信息光学智慧树知到课后章节答案2023年下北京工业大学北京工业大学绪论单元测试1.傅里叶光学是专门研究二维光信息的科学，是光学与通信理论的结合，是当代信息科学的一部分。

这一说法是否正确？A:错误 B:正确答案:正确第一章测试1.可用来描述点光源复振幅分布的基元函数是（）。

A:脉冲函数（δ函数） B:三角形函数 C:矩形函数 D:圆柱函数答案:脉冲函数（δ函数）2.用来描述激光器出射光斑光场复振幅分布的基元函数是（）。

A:三角形函数 B:矩形函数 C:高斯函数答案:高斯函数3.下列关于互相关与卷积运算关系的表达式正确的是（）。

A:★B:★C:★D:★答案:★4.互相关是衡量两个信号之间相似度。

两个完全不同的、毫无关系的信号，对所有的位置，它们互相关的结果应该为（）。

A:1 B:无穷大 C:0答案:05.函数的傅里叶变换为（）。

A:0 B:1 C: D:答案:1第二章测试1.线性空间不变系统的输入与输出之间的关系可以通过（）运算可以表示。

A:输入与脉冲响应相关 B:输入与脉冲响应乘积 C:输入与脉冲响应卷积答案:输入与脉冲响应卷积2.在傅里叶光学中，把光的传播、成像、信息处理等都以系统是（）去分析各种光学问题的。

A:非线性系统 B:线性系统 C:其他系统答案:线性系统3.一个空间脉冲在输入平面位移，线性系统的响应函数形式不变，只产生相应的位移，这样的系统称为（）。

A:空间不变系统或位移不变系统 B:其它系统 C:时不变系统答案:空间不变系统或位移不变系统4.对于线性不变系统，系统的输出频谱是输入函数频谱与系统（）的乘积。

A:本征函数 B:脉冲响应 C:传递函数答案:传递函数5.根据抽样定理，对连续函数进行抽样时，在x、y方向抽样点最大允许间隔、分别表示该函数在频域中的最小矩形在和方向上的宽度。

）A: B:C:第三章测试1. 基尔霍夫衍射积分公式从理论上证明了光的传播现象能看作（ ）系统。

A:非线性系统 B:线性系统 C:线性空间不变系统 答案:线性空间不变系统2.圆对称函数的傅里叶变换式本身也是圆对称的，它可通过把空间坐标转换到极坐标系中计算求出，我们称这种变换的特殊形式为（）。

信息光学 第5章 光学全息

信息光学 第5章 光学全息

§5-2 光学全息原理
三、例题
两束夹角为 = 45o的平面波在记录平面上产生干涉，已知光波 波长为632.8nm，求对称情况下（两平面波的入射角相等）该平面 上记录的全息光栅的空间频率。 O ( x , y ) = exp[jkxsin( /2)] x R R ( x , y ) = exp[-jkxsin( /2)] U(x, y) = exp[jkxsin( /2)] + exp[-jkxsin( /2)] z
六、全息照相的发展简史
第一代全息图（汞灯记录，可见光再现）
1948年，Gabor 提出 “波前重现” 理论
目的：改善电子显微镜的分辨率。
效果：因光源（汞灯）相干性差，成像质
量很差，没引起普遍关注。
作用：借助于把相位差转换成强度差的思
想，解决了全息照相的基本问题，把位相 编码成记录介质能识别的物理量 。

I(x, y)=U(x, y)· U*(x, y)=|O|2+|R|2+O· *+O*· R R =2+2cos[kx﹒2sin( /2)] O H
2 sin 2 I ( x, y) 2 2 cos2x
§5-2 光学全息原理
三、例题
R x
2 sin 2 I ( x, y) 2 2 cos2x
其调制度为1，空频为：
f
代入 = 45o， = 632.8nm， 计算得：
2 sin 2

f =1209.5 lp/mm
§5-2 光学全息原理
四、全息实验装置 相干光源——激光器 光的相干性包括时间相干性和空间相干性。 要求光束的相干长度足够长，相干面积足够大。

信息光学第五章

信息光学第五章
当 C ( x, y ) R( x, y )
2 2
U ' ( x, y) R( O R ) O R O R
2
2
2
*
2
5.3 基元全息图分析
平面波与平面波；平面波与球面波；球面波与球面波
A2

A1
5.4 平面全息图及其衍射效率
全息图的分类： •记录介质的膜厚：平面全息图、体积全息图 •透射函数的特点：振幅型、相位型（折射率型 表面浮雕型） •物光特点：Fresnel Fraunhofer Fourier •再现照明光种类：激光再现、白光再现 •再现照明光与衍射光的方向：透射型、反射型 •再现像特征：像面全息、彩虹全息、360度合成全息、真彩色全息
(2) 用空间调制的光波作参考光记录
像全息图
线模糊和色模糊
像全息图
像全息图
相位全息图
2 I ( x, y ) O( x, y ) R( x, y ) O0 R02 2O0 R0 cos( o r ) 2
H ( x, y) I ( x, y)
tH ( x, y) t0e
xLeabharlann 傅里叶变换全息图的两个特例
(1) 用空间调制的光波再现
tc ( x0 , y0 )
tc O
Tc t H
像平面上：F.T .1 Tc tH F.T .1 Tc F.T .1 tH tc F.T .1 tH
傅里叶变换全息图的两个特例
(2) 用空间调制的光波作参考光记录
O( x, y) O( x, y) e jo ( x, y )
I ( x, y ) O ( x, y )
位相的重要性：

信息光学知到章节答案智慧树2023年苏州大学

信息光学知到章节答案智慧树2023年苏州大学

信息光学知到章节测试答案智慧树2023年最新苏州大学绪论单元测试1.“信息光学”又称为 ____。

参考答案:null第一章测试1.高斯函数的傅里叶变换是（）参考答案:2.函数的傅里叶变换是（）。

参考答案:3.某平面波的复振幅分布为，那么它在不同方向的空间频率，也就是复振幅分布的空间频谱为（）。

参考答案:，4.圆域函数Circ（r）的傅里叶变换是。

（）参考答案:对5.尺寸a×b 的不透明矩形屏，其透过率函数为rect(x/a)rect(y/b)。

（）参考答案:错6.卷积是一种 ____，它的两个效应分别是____和____，两个函数f(x, y)和h(x, y)卷积的积分表达式为____。

参考答案:null7.什么是线性空不变系统的本征函数？参考答案:null8.基元函数是不能再进行分解的基本函数单元，光学系统中常用的三种基元函数分别是什么？参考答案:null第二章测试1.在衍射现象中，当衍射孔径越小，中央亮斑就____。

参考答案:null2.点光源发出的球面波的等相位面为____，平行平面波的等相位面为____。

参考答案:null3.平面波角谱理论中，菲涅耳近似的实质是用____来代替球面的子波；夫琅和费近似实质是用____来代替球面子波。

参考答案:null4.你认为能否获得理想的平行光束？为什么？参考答案:null5.菲涅尔对惠更斯的波动光学理论表述主要有哪两方面的重要贡献？参考答案:null6.已知一单色平面波的复振幅表达式为，请问该平面波在传播方向的空间频率以及在x，y，z方向的空间频率分别是什么？参考答案:null第三章测试1.物体放在透镜（）位置上时，透镜的像方焦面上才能得到物体准确的傅里叶频谱。

参考答案:前焦面2.衍射受限光学系统是指（），仅考虑光瞳产生的衍射限制的系统。

参考答案:不考虑像差的影响3.相干传递函数是相干光学系统中（）的傅里叶变换。

参考答案:点扩散函数4.（）是实现对空间物体进行信息处理和变换的基本光路结构。

信息光学导论第五章

信息光学导论第五章

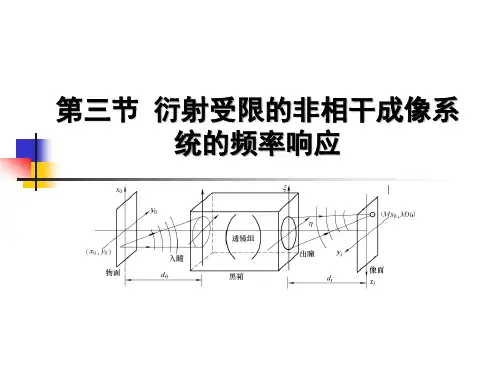
第五章傅里叶变换光学与相因子分析方法5.1 衍射系统波前变换◆引言现代光学的重大进展之一，是引入“光学变换”概念，由此发展而形成了光学领域的一个新分支——傅里叶变换光学，泛称为变换光学(transform optics)，也简称为博里叶光学，它导致了光学信息处理技术的兴起．现代变换光学是以经典波动光学的基本原理为基础，是干涉、衍射理论的综合和提高，它与衍射、尤其与夫琅禾费衍射息息相关．对于熟悉经典波动光学的人们来说，由于他们有着较充分的概念储备和较充实的物理图像，因而具备更为有利的条件，去深刻而灵活地掌握现代变换光学．◆衍射系统及其三个波前如图所示，一个衍射系统以衍射屏为界被分为前后两个空间．前场为照明空间，充满照明光波；后场为衍射空间，充满衍射光波．照明光波比较简单、常为球面波或平面波，这两种典型波的等幅面与等相面是重合的，属于均匀波，其波场中没有因光强起伏而出现的图样．衍射波较为复杂，它不是单纯的一列球面波或一列平面波，其等幅面与等相面—般地不重合，属于非均匀波，其波场中常有光强起伏而形成的衍射图样．在衍射系统的分析中，人们关注三个场分布：其中，入射场是照明光波到达衍射屏的波前函数；出射场是衍射屏的透射场或反射场，它是衍射空间初端的波前函数，它决定了整个衍射空间的光场分布；而衍射场是纵向特定位置的波前函数。

由此可见，整个衍射系统贯穿着波前变换：波前这是衍射屏的作用：波前这是波的传播行为．由一个波前导出前方任意处的另一个波前，这是波衍射问题的基本提法，亦即波传播问题的基本提法．标量波的传播规律己由惠更斯—菲涅耳—基尔霍夫理论(HFK 理论)给出．在常见的傍轴情形下，其表达式为其积分核为，这是一个球面波的相因子形式．换言之HFK理论是—个关于衍射的球面波理论——衍射场是衍射屏上大量次波点源所发射的球面被的相干叠加．◆衍射屏函数及其三种类型我们已经同多种衍射屏有过交道，现在给山衍射屏函数的一般性定义，以定量地描述衍射屏的自身特征：即，屏函数(screen function)等于出射波前函数与入射波前函数之比．对于透射屏，可称作复振幅透过率函数；对于反射屏，可称作复振幅反射率函数．无疑，屏函数通常也是复函数，含模函数和辐角函数．唯象地看，实际上的衍射屏可分为三种类型，振幅型、相位型和相幅型．若为常数，仅有函数，则该衍射屏为振幅型，凡孔型衍射屏均系振幅型．若为常数，仅有函数，则该衍射屏为相位型，这在此之前似乎少见，其实，闪耀光栅不论其为透射的或反射的，均是一个相位型衍射屏，下一节即将研究的透镜相位衍射元件．当然，更为一般的情况是相幅型衍射屏，、皆为函数形式，即不仅出射场的振幅分布有别于入射场的，而且出射场的相位分布也有别于入射场的。

信息光学(傅里叶光学)Chap5-4

信息光学(傅里叶光学)Chap5-4


P , dd
2



∴P*()= P(), P()2= P(), ∫∫P()2d d = 光瞳总面积
#
§ 5-4 衍射受限的非相干成像系统的频率响应 三 .OTF的计算.
? fx, f y

P , P d f , d f dd Px, y dxdy
i x i y

f ,f
x y
两个错开光瞳的重叠面积s f x ,f y 光瞳总面积s0
两个错开光瞳的相对位置, 与指定空频分量相对应.
光瞳为简单函数时,OTF可以直接计 算,复杂情况时要用面积仪或计算机.
§ 5-4 衍射受限的非相干成像系统的频率响 应三 .OTF的计算 例1.出瞳为边长l 的正方形
§5-3衍射受限的相干成像系统的频率响应 二．相干传递函数 例3.
Ug
3
h
Ui
*
0
=
-1
xi
每个狭缝产生会聚球面波,将孔径(单缝)的F.T.投射到像平面上. 产生的位移的衍射图样相干叠加. Gg Gi
f
1
Hc
-1/d 0 1/d
fx
f0
0
-f0
=
-1/d 0 1/d
fx
#
§5-3衍射受限的相干成像系统的频率响应 二．相干传递函数 例3.
相干传递函数:
Hc fx , f y


(d f ) 2 (d f ) 2 i x i y circ l/2
circ
2 2 fx fy f0
l f0 2d i
为沿各个方向的 截止频率(像面截止频率) #

信息光学第五章

信息光学第五章

全息显微术、全息信息存储等。
§5-1 全息照相的基本原理
全息术的基本思想：波前记录与波前再现。
全息图的记录
全息图的再现
一、波前记录：干涉记录
记录介质只对光强有响应，不能记录波前携带的位相信息， 只有使位相的空间调制转换为强度的空间调制才可能实现完整
信息的波前记录：干涉法可实现这一转换。
物光复振幅：O ( r, t ) AO ( r )eiO ( r )t 参考光复振幅：R( r, t ) AR ( r )ei R ( r )t 记录介质上的总光场为： A( r, t ) O ( r, t )＋R ( r , t ) 对应的总光强为 I(r)= A( r, t ) A* ( r , t )
在底片上所产生的光强分布为
k1 2 2 I ( x, y ) O R R O exp i x x0 y y0 2 z0 k1 k1 2 2 2 2 * i x xR y yR RO exp i x xR y y R , y) o ( x, y)
全息图实际上就是干涉图：第三项是干涉项，在干涉条纹的 幅值以及条纹位置信息中包含有物光振幅和位相的信息，它
们分别受到参考光振幅和位相的调制。
二、波前再现：衍射再现
1.用原参考光波照明
再现光与原参考光波
的传输方向与波前分 布都相同！
用原参考光波照明全息图时，全息图的透射光场分布为：
用不同的参考光记录不同的物体，用相应的再现光就可以再
现不同的像。
可在同一张全息底片上对不同的物体记录多个全息图像， 只须每记录一次后改变一下参考光相对于全息底片的入射角 即可。 使重现光与原参考光的波长不同，则重现像的尺寸就会改
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2011年8月1日安徽卫视的水浒传首映礼3d全息投影 效果舞台，利用全息照相投影出来。
全息防伪
泰国普吉岛江西冷购物广场
2015年春节联欢晚会李宇春《蜀绣》
2016年9月4日张艺谋导演晚会《最忆是杭州》
全息图记录和再现小结 波前记录是一种干涉效应，它使振幅和位相调制的信息变换
为干涉图的强度调制信息；
则其合振幅 Ar,t Or,t Rr,t
光强度
AO r eiO rt AR r eiR rt
I r,t Ar,tA*r,t Or,t Rr,tOr,t Rr,t*
I r,t Or,t Rr,tOr,t Rr,t*
I r,t Rr,t2 Or,t2 R*r,tOr,t Rr,tO*r,t
息图和离轴全息图。
O
同轴全息图
R
粒子场全息测试
油珠分布 空间物场分布 喷水分布
2.按全息图结构与观察方式：透射全息图和反
射全息图。
透射全息图 物光和参考光在全息图同一侧
反射全息图
O
R
O
R
观察者和参考光在全息图两侧
3.按全息图复振幅透过率：振幅型全息图与位相型 全息图；后者又分为折射率型和表面浮雕型两种。
或写成：
Ir,t R 2 O 2 2O R cosR rO r
是干涉项， 清楚地表明：它包含了物光波的振幅和相位信息。 参考光波作为载波，其振幅和相位均受到物光波的调制(调幅、 调相)。参考光波的引入，使物光波的相位分布转换成了干涉条 纹的强度分布（衬比度、条纹间距、方向）
时间因子已经不出现在干涉的效应里面，而只出现了空间位相差
英国伦敦帝国大学工作
接着E.Leith和J.Upatnieks就用激
光拍摄成了完善的全息照片，在
一张平面全息图底片的后面重现
出原物逼真的三维形象，令人赞
叹不已。
视差效应
立体电影就是用两个镜头如人眼那样的拍摄装置，拍摄下景物的双视点
图像，再通过两台放映机，把两个视点的图像同步放映，使这略有差别 的两幅图像显示在银幕上，这时如果用眼睛直接观看，看到的画面是重 叠的，有些模糊不清，要看到立体影像，就要采取措施，使左眼只看到 左图像，右眼只看到右图像，如在每架放影机前各装一块方向相反的偏 振片，它的作用相当于起偏器，从放映机射出的光通过偏振片后，就成 了偏振光，左右两架放。
第5章 光学全息照相
5.0 概述
一、什么是全息照相？
全息照相是一种摄影技术
全息照相得到的是真正立体的、三维的、 空间的原始像
二、全息技术是怎样发明的
早 在 1948 年 ， 英 籍 匈 牙 利 物 理 学 家 D.Gabor就根据光的干涉和衍射原理， 提出了重现波前的全息照相理论。
12年后激光器问世，第一台红宝石激光器 诞生，解决了相干光源的问题。
➢全息干板（胶片）的结构：
感光层：银盐乳胶，由照相明胶、卤化银颗粒、及适量的补 加剂（包括坚膜剂、增感剂、稳定剂等）组成。明胶不仅是 感光层的成膜物质，而且具有很好的分散作用，使超微粒的 卤化银晶粒(0.03um-0.08um)能均匀分散其中。
底层：使亲水的乳胶层牢固地粘附于疏水的玻璃片上。
片基：玻璃或塑料片，作为支撑体。
显微镜下观察的干涉条纹。 从空间频率上说，大概每 毫米分布上千条条纹—— 与光路布置有关。
全息图的记录和重现
扩束镜
直径1-2mm
激光器
透镜会聚光 焦距：5mm 放大倍数：40
漫散射 全息图的记录
曝光——根据底片的灵敏度 的不同，曝光时间有所不同。
底片经过显影、定影处理。
全息图的重现
重现光束
感光板
防晕层：由吸光物质和粘接剂组成，防止曝光时背面反射光。 用于拍摄反射全息图的厚全息感光板，不需要防晕层。
➢感光过程：光化学过程 银盐乳胶吸收光子生成不可见的潜像，显影处理后
得可见的像，定影后成为永久像。
潜像形成过程：银盐乳胶吸收光子后，分解成一些 金属银小斑点（显影中心），在显影过程中，这些细小的 显影中心使整个卤化银晶粒变成金属银而沉淀下来，没有 曝光或没有吸收足够能量的晶粒保持不变，定影时可除去 未曝光的卤化银晶粒，而留下金属银。
全息照相采用物理光学的干涉和衍射。利用干涉原理，
通过引入一个与物光波相干的参考光波与物光波干涉，将 物光波中的振幅和相位信息以干涉条纹（干涉图）的形式 记录在某种介质上。然后再利用光波衍射的原理，通过光 波的衍射，再现原始物光波，从而再现原物体的三维像。
全息的意义是记录物光波的全部信息。 全息照相过程分为记录和重现两个步骤。
性的，也不一定是单调的，因而干涉条纹的疏密、取向、强弱和对
比度都是在随处变化。但其变化不是随机的，而是以φR随空间较 规则的变化为标准，把物光波的位相分布φO以光强度变化的形式
反应出来，而振幅则以条纹的调制深度被记录下来。
干涉图记录到记录介质上形成全息图
全息记录介质有多种。常用的是涂有卤化银乳胶的银盐感光板（或胶片）。 经适当显影、定影等处理后，就得到全息图。
重现光束 感光板
虚像
实像
实像和虚像的区别：
实像——在屏幕上可以看到。 虚像——在屏幕上看不到，人眼可以看到。
5.1.2 记录与重现数学分析
记 录 ：
设在全息干板平面上，由物体散射的物光波的复振幅表示为：
O r,t
AO
r
e
i
O rBiblioteka 位相t （物光） 瞬时位相
振幅
参 考 光 波 ：R r, t AR r eiR r t （参考光）
原始像 +1级衍射
共轭像 -1级衍射
当用共轭参考光重现时，其透射光场为
Arec r,t R*r,t r
位相畸变 共轭像
R* 0 O 2 R 2 R*R*O R 2O*
Arecr,t R0 O 2 R 2 RR*O R2O*
Arecr,t R* 0 O 2 R 2 R*R*O R 2O*
R 2 O 2 R*O RO*
参参似物纹分 参考别考考均光强前光包光光匀波度两波含波波分在分项是了在，布介布基载物介。质来本R波光质面讲为上，波面上是常是物和的的慢数常光物强强变或波光数度度化作波近，为的分分的似是调共布布，为直制轭，且,常流一波。一比数项般。是般参，，用可物是考该对以光平不光项波用波面均波是前于对波匀弱均再波参或的很匀前考现球，多再光分无面现波但。布用波。的相、。作调对或为制条近，
在记录面上进行叠加的基本光波形式，可归纳为或可分解为 以下几种情况：
（1）平面波与平面波 （2）平面波与球面波 （3）球面波与球面波
基元全息图：由上述基本光波干涉所形成的干涉条纹分布。 任何一个全息图都是由许多基元全息图线性组合而成。
基元全息图的干涉条纹形成、及其分布形式有以下几种情况：
（1）平面波与平面波干涉形成的直条纹。在空间中, 等强度 面是等间距的平面, 在某截平面上, 等强度线是直线，条纹间 距与两平面波的夹角有关。
从空域来看，物体可看作是许多相干点源的集 合，物体上每一点发出的球面波，与参考光相 干涉，所形成的基元全息图称为基元波带片。
从频域来看，物光波可看作是许多具有不 同相位、沿不同方向传播的平面波的线性 叠加,每一平面波分量与参考平面波干涉而 形成的基元全息图是一些平行直条纹，称 为基元光栅。
综上所述：抛开具体记录光路, 从分解的角度来看,物体的 形状再复杂，物函数总可分解为平面波或球面波的复杂组合。 因而全息图的干涉花样也可分解为平面光波或点光源发出的 球面波与参考光的干涉。
Ir,t R 2 O 2 2O R cosR rO r
Ir,t
R
2
O
2
1
2O R2
R O
2
cosR
r O
r
2O R 条纹对比度： V O 2 R 2
条纹形状由位相差 φR-φO 决定。因此，全息图片经曝光、显
影、定影等处理后，不仅记录了关于两光波的强度信息，也记录了
他们的振幅和位相信息。可以想象，φR-φO的空间变化不一定是线
6种分类是相互穿插、相互渗透。
5.2 菲涅耳全息图
O
平
面
R
波 入
射
几何投 菲涅尔衍射区 影区
夫琅禾费衍射区
物光波：波前分布因物体形状及特点而异,具有复杂的波前分布。
参考光波：为了简化，常采用平面光波或球面光波。
因此，全息图中的条纹分布一般是十分复杂的。
5.2.1基元全息图的几何模型
基元（点源）全息图：物体可看成点源的线性组合。故可将点 源全息图看作基元全息图。由单一物点发出的光波与参考光波 干涉所构成的全息图。任何一种全息图均可以看做是许多基元 全息图的线性组合。
R O 平面透射全息
R O 体透射全息
R O 体反射全息
物光波的振幅给出物体的亮度(强度)信息，相 位给出物体的方位（深度和位置）信息
(2) 平面波与发散球面波所形成的条纹。在空间中, 等强度的 面是旋转抛物面, 在某一截面(用平面记录介质记录时)是曲线 (弧形、或圆环, 与接受面的位置有关)。
振幅型全息图（照相底片）：干涉条纹是以浓淡相间的黑 白条纹记录在干板上；重现时黑色部分吸收光能量。
位相型全息图（玻璃）：漂白，光强度不发生变化，位相 发生变化。1）折射率变化。2）厚薄不同-0.1微米。
4.按全息底片与物的距离：菲涅耳全息图、像面 全息图和傅里叶变换全息图。
菲涅耳全息图：物体与全息底片的距离较近时拍摄的。
说 明 ：
上述两式表现曝光时的入射光场和显影后的透射光场之间 的高度非线性变换关系，似乎线性系统对全息照相理论不 能 起 作 用 。 但 从 物 光 场 O(x,y) 到 透 射 光 场E3分 量R的2O 或 E3 R 2O* 变换却是完全线性的。
英女王全息图