信息光学(共计626页,共计3部分)_部分1
- 格式:pptx
- 大小:5.21 MB
- 文档页数:205






湖北省高等教育自学考试大纲课程名称:信息光学课程代码:7076第一部分课程性质与目标一、课程性质与特点信息光学是应用光学、计算机和信息科学相结合而发展起来的一门新的光学学科,是信息科学的重要组成部分,也是现代光学的核心。
本课程主要从两个方面介绍信息光学的基本内容:一是信息光学的基础理论,包括线性系统理论、标量衍射理论、传递函数理论等;二是信息光学的主要应用,包括光学全息、计算全息、空间滤波、光学相干和非相干处理等。
二、课程目标与基本要求通过本课程的教学,使学生了解和掌握光信息科学的基本理论及基本技术,了解光信息科学的实际应用,培养学生理论联系实际,开拓学生理论用于实践的方法和创新思路,提高学生解决实际问题的能力。
三、与本专业其他课程的关系《信息光学》是光机电一体化工程专业的一门专业课,其先修课程主要包括普通物理、高等数学、傅立叶变换、光学等课程。
第二部分考核内容与考核目标第一章线性系统分析一、学习目的与要求本章基本内容为:常用数学函数,卷积与相关,傅立叶变换性质及定理,线性系统分析,二维光波场分析。
本章是本课程的基础,要求学生在解决光学问题中能熟练运用其性质和定理,线性系统与光学系统的关联,加深对空间频率、空间频谱概念的理解。
二、考核知识点与考核目标(一)(重点)识记:常用数学函数;卷积;互相关、自相关;傅立叶变换;线性系统;线性平移不变系统理解:傅立叶变换性质;线性系统分析;空间频率、空间频谱;应用:单色平面波空间频率的计算(二)(次重点)识记:卷积、相关的性质;理解:傅立叶变换基本定理第二章标量衍射理论一、学习目的与要求本章基本内容为:基尔霍夫积分定理;基尔霍夫衍射公式;菲涅耳衍射和夫朗和费衍射;透镜的傅立叶变换特性。
本章是教学的重点,是信息光学的基础,要求学生掌握标量波衍射理论,侧重利用菲涅耳衍射与卷积、夫朗和费衍射与傅立叶变换关系解决问题;掌握光波通过透镜的相位分布,透镜的傅立叶变换特性及孔径对透镜实现傅立叶变换的影响。



信息光学部分章节小结第一部分:数学基础一 几个常用函数(1)矩形函数:该二维矩形函数可用来描述无限大不透明屏上矩形孔的透过率。
(a>0,b>0)(2)sinc 函数:sin by b y a x a x b y c a x c b y a x /)/sin(/)/sin()(sin )(sin ),ππππ∙=∙= (a>0,b>0) (3)阶跃函数: (4)符号函数:(5)三角函数:二维三角函数可用来表示一个光瞳为矩形的非相干成像系统的光学传递函数 (6)高斯函数:(7)圆域函数:(8)δ函数: ⎪⎩⎪⎨⎧≤≤=∙=others b y a x by rect a x rect b y a x rect ,02,2,1)()(),(⎪⎪⎪⎩⎪⎪⎪⎨⎧>=<=0102100)(a x a x a x a x step ⎪⎪⎪⎩⎪⎪⎪⎨⎧<-=>=010001)sgn(a x a x a x a x ⎪⎩⎪⎨⎧<--=ΛΛ=Λothers b y a x b y a x b y a x b y a x ,01,),1)(1()()(),(0,]})()[(exp{),(22>+-=b a b y a x b y a x Gauss πothers r y x r r y x circ r r circ 01{)()(0220220≤+==+= 1),( 20,),( 1000000⎪⎪⎭⎪⎪⎬⎫=--︒⎩⎨⎧==∞=--︒⎰⎰∞+∞-dxdy y y x x others y y x x y y x x δδ(9)comb 函数:∑--==nm ny y mx x y x y y comb x x comb y y x x comb ,00000000),()()(),(δ 二 几种重要的数学运算1 卷积:卷积的几个重要性质: (1) 线性性质:{),(),(),(),(),()},(),(y x g y x bh y x g y x af y x g y x bh y x af *+*=*+(2) 卷积符合交换律:),(),(),(),(y x f y x h y x h y x f *=*(3) 卷积符合结合律:[][]),(),(),(),(),(),(y x g y x h y x f y x g y x h y x f **=**(4) 卷积的坐标缩放:若),(),(),(y x g y x h y x f =*,则),(1),(),(by ax g ab by ax h by ax f =* (a,b 均不等于0) (5) 卷积位移不变性:若),(),(),(),(y x f y x h y x h y x f *=*,则),(),(),(),(),(000000y y x x g y y x x h y x f y x h y y x x f --=--*=*--(6) 函数),(y x f 与δ函数的卷积:),(),(),(0000y y x x f y y x x y x f --=--*δ2 相关互相关:自相关:3 傅立叶变换 傅立叶变换对:正变换 ⎰⎰+∞∞-+-=dxdy y f x f j y x f f f F y x y x )(2exp[),(),(π 逆变换 ⎰⎰+∞∞-+=y x y x y x df df y f x f j f f F y x f )(2exp[),(),(π频谱函数),(y x f f F 一般是复函数,因此:[]),(exp ),(),(y x y x y x f f i f f F f f F φ= 傅立叶变换的重要性质:(1)线性 a,b 为任意常数ηξηξηξd d y x h f y x h y x f y x g ),(),(),(),(),(--=*=⎰+∞∞-),(),(),(),(),(y x g y x f d d y x g f y x e fg ⊗=++=⎰⎰*ηξηξηξηξηξηξηξηξηξd d f y x f d d y x f f y x f y x f y x e ff ),(),(),(),(),(),(),(**⎰⎰⎰⎰--=++=⊗=),(),(y x bg y x af +⇔(,)(,)x y x y aF f f bG f f +(2)缩放定理 (3)位移定理 [])(2ex p ),(),(b f a f i f f F b y a x f y x y x +±⇔±±π),()](2exp[),(ηξηξπ y x f f F y x i y x f ⇔+±(4)卷积定理),(),(),(),(),(),(),(),(y x y x y x y x f f G f f F y x g y x f f f G f f F y x g y x f *⇔⇔* (5)互相关定理),(),(),(),(),(),(),(),(y x y x y x y x f f G f f F y x g y x f f f G f f F y x g y x f ⊗⇔⇔⊗***由互相关定理可以推导出自相关定理。
信息光学绪论教材《信息光学》,苏显渝,科学出版社参考书目1《近代光学信息处理》,宋菲君,北京大学出版社2《光学传递函数及其数理基础》,麦伟麟,国防工业出版社3《傅立叶光学》,吕乃光,机械出版社现代光学的发展光学是一门古老的学科伽利略,牛顿―――几何光学惠更斯、菲涅尔、夫琅禾费---波动光学麦克斯韦――――电磁波爱因斯坦――――光量子已形成了完整的理论体系以及与理论配套的试验方法。
信息光学经历40年的发展,已形成较为完整的学科。
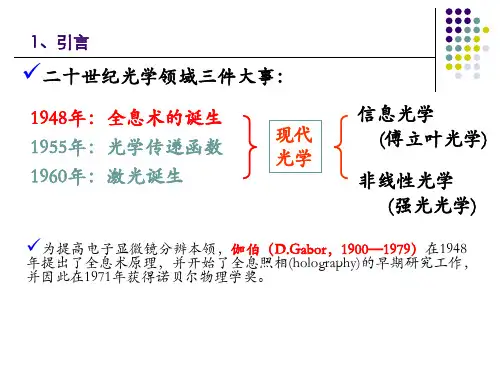
什么是信息光学信息光学产生于三件大事:(1)1948年全息术诞生,物理学家们第一次精确地拍摄下一张立体的物体像,它记录了光波所携带的全部消息(这正是“全息”名称的来历) ;(2)1955年提出“光学传递函数”概念,用于评价光学镜头质量;(3)1960年激光器诞生,出现了有高度相干性的光源。
构成了信息光学的基础,而透镜的傅里叶变换效应则,构成了信息光学的理论框架。
1961年,中国第一台激光器王之江,中科院院士、物理学家邓锡铭,光学、激光专家光学照相:I (振幅,光强),1792,黑白照相λ(波长,频率),1908,彩色照片Φ(位相),1935,相衬显微镜I,λ,Φ——全息照相在光学中,从“空域”,“空间坐标系”观念对图像的描述过渡到用“频域”或“频率坐标系”描述。
开辟了新天地,由传统的波动光学,在引入傅立叶变换后,形成了新的学科--信息光学(或傅立叶光学)信息光学是用数学中的傅里叶变换和通信中的线性系统理论来处理光学问题的学科.光学工程师不仅限于用光强、振幅或透过率的空间分布来描述光学图像。
还用频率的分布和变化来描述光学图像,一副图像是由缓慢变化的背景、组的轮廓等比较低的“空间频率”成分和急剧变化的细节等比较高的“空间频率”成分构成的。
光学工程师和电气工程师的共同语言:用共同的观念(频率)、共同的理论体系(线性系统)、共同的方法(傅里叶变换)来处理光学和通信这两个不同领域中的课题,使它们在“信息学”的范畴内统一起来。