有价格折扣的经济订货批量模型

什么是经济订货批量模型?经济订货批量模型公式什么是经济订货批量模型?经济订货批量模型公式经济订货批量模型(Economic Order Quantity, EOQ)：又称整批间隔进货模型EOQ模型，是目前大多数企业最常采用的货物定购方式.该模型适用于整批间隔进货、不允许缺货的存储问题，即某种物资单位时间的需求量为常D，存储量以单位时间消耗数量D的速度逐渐下降，经过时间T后，存储量下降到零，此时开始定货并随即到货，库存量由零上升为最高库存量Q，然后开始下—个存储周期，形成多周期存储模型。

经济订货批量模型最早由于1915年提出的,该模型有如下假设:(1)需求率已知,为常量.年需求量以D表示,单位时间需求率以d表示.(2)一次订货量无最大最小限制.(3)采购,运输均无价格折扣.(4)订货提前期已知,为常量.(5)订货费与订货批量无关.(6)维持库存费是库存量的线性函数.(7)补充率为无限大,全部订货一次交付.(8)不允许缺货.(9)采用固定量系统.EOQ 经济订货批量EOQ的概念，公式，案例分析，公式推导证明，适用情况,缺陷1.经济订货批量EOQ 的概念经济订货批量是固定订货批量模型的一种，可以用来确定企业一次订货的数量。

当企业按照经济订货批量来订货时，可实现订货成本和储存成本之和最小化。

2.公式为Q* = SQRT(2*DS/C)Q*-- 经济订货批量D -- 商品年需求量S -- 每次订货成本C --单位商品年保管费用3.案例分析仓储的管理很类似于生活中自来水水塔现象：水塔是个蓄水池，不停的漏水，快漏完的时候，就要迅速加水至满，保持平衡。

对于某医药配送企业仓库管理，可以看作它是集中大量采购，然后慢慢销售；快完的时候，在集中大量采购，如此循环；为了便于建模，我们把上面问题看的再理想化些：水塔的水是均匀漏的，加水时是瞬间加满的；该医药配送企业的某种药品的销售也是均匀的已一个固定的速度出库，采购的动作也是瞬间完成的；要解决的问题描述(水塔现象的对照)1.水塔负责的小区居民，一年有1000吨的用水量，每吨水的价格1元，每吨水的保管费用平均为一年元，每次水泵抽水至水塔需要费用2元；那么我们根据这些数据，想到的结论是什么呢？那就是这个水塔要建立多大，每隔多长时间送一次水？一年的总费用是多少？2 .该医药配送企业某种药品一年销售10000箱，每箱进价100元，每箱货的保管费用平均为一年5元，每次供应商送货的手续费170元；根据这个数据，我们想知道：每次采购多少箱？多长时间采购一次？一年的总费用是多少？年费用的计算该医药配送企业一年的总费用计算公式=商品的总进价+全年的保管费+全年订货手续费=每箱进价*销售总箱数+(每箱年保管费/2*销售总箱数)/订货次数+每次订货手续费*订货次数这里有人概念容易误解，就是全年的保管费的计算；很容易让人感觉:全年的保管费=每箱年保管费*销售总箱数;下面我举一个最简单的例子否定上面想法：比如仓库月初进了30箱货，每箱每天的保管费用为1元，那么到月底的时候保管总费用是不是(1元/箱.天)*30箱*30天=900元呢？实际上你要考虑到箱子在均匀出库。

带有价格折扣的经济订货量模型带有价格折扣的经济订货量模型在现代商业社会中，企业如何制定合理的订货量是一个关键问题。

其中一个重要因素是价格折扣，即供应商给予企业的激励性价格优惠。

本文将探讨带有价格折扣的经济订货量模型，以帮助企业在订货决策中获得最大利益。

首先，订货量的决策对企业效益的影响必须得到充分考虑。

企业在订货过程中需要平衡存货成本和销售收入，从而实现最大的利润。

价格折扣为企业提供了一种诱因，通过订购更多的产品来获得价格优惠，从而降低存货成本。

其次，为了建立模型，我们需要定义一些关键变量。

订货量、价格折扣、产品成本和市场需求是模型中需要考虑的主要因素。

订货量表示企业在每一次订购中所采购的产品数量。

价格折扣表示供应商给予的降价幅度。

产品成本是企业购买产品的成本，通常与订货量成正比。

市场需求是指企业所经营的市场对产品的需求情况。

接下来，我们将建立一个简化的经济订货量模型来分析价格折扣的影响。

假设市场需求是确定的，即在一段时间内保持恒定。

我们引入一个线性成本函数来描述产品成本，成本与订货量成正比。

此外，我们假设价格折扣是一个分段函数，即当企业订货量达到一定数量时供应商会给予相应的折扣。

在这个模型中，问题转化为寻找一个最佳的订货量，使得企业利润最大化。

考虑到存货成本和销售收入，我们可以使用一个简单的公式来表示企业的利润：利润 = 销售收入 - 存货成本其中，销售收入等于产品的售价乘以销量，存货成本等于产品成本乘以订货量。

我们可以通过求解这个问题的最优解来确定最佳的订货量。

在模型中，企业的利润随着订货量的增加而增加，但是当订货量超过一定阈值时会导致存货成本的大幅增加，从而降低利润。

然而，价格折扣为企业提供了一种降低存货成本的机会。

当价格折扣与存货成本的差额超过一定比例时，企业将受益于增加订货量。

通过计算不同价格折扣下的最优订货量，我们可以确定哪个价格折扣对企业最有利。

总结而言，带有价格折扣的经济订货量模型能够帮助企业在订货决策中获得最大利益。

一、经济订货批量1、某产品的市场需求率是500个/周，订货费为每次200元，单位持货成本系数为每周每个货物2元。

补货提前期为2天，计算经济订货批量和订货点。

2、牙膏厂的牙膏年生产量是6万箱，牙膏的市场需求为每年2.6万箱，生产线每次启动的费用是1350元，每箱牙膏的生产费用是45元，工厂保管牙膏的年费率是生产成本的30%。

计算牙膏的经济生产批量。

二、数量折扣订货批量•某农产品的市场需求为每周100吨，进货单价为每吨780元。

订货费为每次500元，每周保管费为每吨单价的2%。

每次订货超过100吨时单价750元，超过300吨时单价730元，超过600吨时单价720元。

计算订货批量.三、安全库存量•1、某饭店的啤酒日销售量为均值10箱标准差2箱的正态分布，向啤酒厂订货的提前期为6天，计算客户满足率为95%的啤酒安全库存。

•2、上题的饭店如果啤酒销售量为每天10箱，订货提前期为均值6天，标准差为1.5天的正态分布，计算客户满足率为95%的啤酒安全库存。

•3、如果该饭店啤酒日销售量和订货提前期都是随机变化，随机变量的分布如上两题，计算客户满足率为95%的啤酒安全库存。

•4．一次订货费用C0=75元，单位物资保管费Ｃ1=10元／吨，提前期1周，已知过去６周的销售量分别为10、16、14、20、16、14（吨），设满足率为84％，求订货策略？（已知Ｐ=84％时，对应ａ=１）四、节约里程法某配送中心P为10个连锁分店A～J送货，配送中心和各连锁分店及各连锁分店之间的位置关系如下图所示，两点间连线上的数字为两店间的路线长度（单位：公里）。

各连锁分店对某种商品的需求量见下表。

配送中心备用2t和4t的货车，限定送货车辆一次巡回距离不超过35公里，求配送中心的最优送货方案。

配送网络图各连锁分店需求量单位：吨计算过程用节约里程法进行求解，步骤如下：第一步：从配送网络图中计算出配送中心至各连锁分店及各连锁分店之间的最短距离，并做出最短距离表第二步：由最短距离表，用“节约算法”计算出各连锁分店之间的节约里程，做出节约里程表第三步：将节约里程由大到小顺序排列，尽量使节约里程最多的点组合装车配送节约里程排序表第四步：根据节约里程排序表和配送车辆载重及行驶里程等约束条件，逐项考查，进行点与点之间的连接。

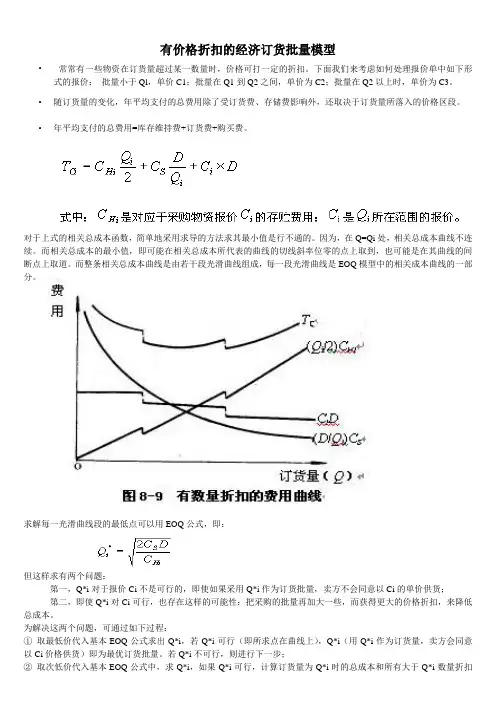
有价格折扣的经济订货批量模型•常常有一些物资在订货量超过某一数量时，价格可打一定的折扣。

下面我们来考虑如何处理报价单中如下形式的报价：批量小于Ql，单价C1；批量在Q1到Q2之间，单价为C2；批量在Q2以上时，单价为C3。

•随订货量的变化，年平均支付的总费用除了受订货费、存储费影响外，还取决于订货量所落入的价格区段。

•年平均支付的总费用=库存维持费+订货费+购买费。

对于上式的相关总成本函数，简单地采用求导的方法求其最小值是行不通的。

因为，在Q=Qi处，相关总成本曲线不连续。

而相关总成本的最小值，即可能在相关总成本所代表的曲线的切线斜率位零的点上取到，也可能是在其曲线的间断点上取道。

而整条相关总成本曲线是由若干段光滑曲线组成，每一段光滑曲线是EOQ模型中的相关成本曲线的一部分。

求解每一光滑曲线段的最低点可以用EOQ公式，即：但这样求有两个问题：第一，Q*i对于报价Ci不是可行的，即使如果采用Q*i作为订货批量，卖方不会同意以Ci的单价供货；第二，即使Q*i对Ci可行，也存在这样的可能性：把采购的批量再加大一些，而获得更大的价格折扣，来降低总成本。

为解决这两个问题，可通过如下过程：①取最低价代入基本EOQ公式求出Q*i，若Q*i可行（即所求点在曲线上），Q*i（用Q*i作为订货量，卖方会同意以Ci价格供货）即为最优订货批量。

若Q*i不可行，则进行下一步；②取次低价代入基本EOQ公式中，求Q*i，如果Q*i可行，计算订货量为Q*i时的总成本和所有大于Q*i数量折扣点（曲线间断点）所对应的总成本，其中最小的总成本所对应的数量为最优订货量。

如果Q*i不可行，（采用Q*i作为订货量，卖方不会同意以Ci的价格供货）重复②直到找到一个可行的为止。

例某医院每月平均使用大约100个急救包，每日的使用量之间没有明显的差异。

采购批量小于75个时，每个急救包的进价35元；采购批量大于或等于75个时，每个急救包的进价为32.5元。