简单的几何图形推理学案平行线的性质同步练习

2022-2023学年人教版七年级数学下册《5.3平行线的性质》同步练习题（附答案）一．选择题1．如图，AB∥EC，则下列结论正确的是（）A．∠A＝∠ECD B．∠A＝∠ACE C．∠B＝∠ACE D．∠B＝∠ACB 2．如图，已知AB∥EF，DE∥BC，则与∠1相等的角有（）A．1个B．2个C．3个D．4个3．已知直线m∥n，将一块含30°角的直角三角板ABC按如图方式放置（∠ABC＝30°），其中A，B两点分别落在直线m，n上，若∠1＝20°，则∠2的度数为（）A．20°B．30°C．45°D．50°4．如图，在△ABC中，∠ACB＝90°，CD∥AB，∠ACD＝40°，则∠B的度数为（）A．40°B．50°C．60°D．70°5．如图，直线a∥b，直线c与a、b相交，∠1＝55°，则∠2＝（）6．如图，将矩形ABCD沿GH折叠，点C落在点Q处，点D落在AB边上的点E处，若∠AGE＝32°，则∠GHC等于（）A．112°B．110°C．108°D．106°7．如图，直线a，b，a∥b，点C在直线b上，∠DCB＝90°，若∠1＝70°，则∠2的度数为（）A．20°B．25°C．30°D．40°8．如图，一条公路修到湖边时，需拐弯绕湖而过，如果第一次拐弯处的∠A是66°，第二次拐弯处的角是∠B，第三次拐弯处的∠C是153°，这时道路恰好和第一次拐弯之前的道路平行，则∠B是（）A．87°B．93°C．39°D．109°9．一艘轮船从A港出发，沿着北偏东63°的方向航行，行驶至B处时发现前方有暗礁，所以转向北偏西27°方向航行，到达C后需要把航向恢复到出发时的航向，此时轮船航行的航向向顺时针方向转过的度数为（）10．一把直尺与一块直角三角板按如图方式摆放，若∠1＝47°，则∠2＝（）A．40°B．43°C．45°D．47°二．填空题（共6小题）11．如图，已知AB∥CD，CE平分∠ACD，交AB于点B，∠ABE＝150°，则∠A为．12．如图，AB∥DE，FC⊥CD于点C，∠ABC＝107°，∠CDE＝130°，点G在BC的延长线上，则∠FCG的度数是．13．如图，直线a∥b，直线c与直线a，b分别交于点A，B．若∠1＝45°，则∠2＝．14．如图，直线a∥b，一块含60°角的直角三角板ABC（∠A＝60°），按如图所示放置，若∠1＝55°，则∠2的度数为．15．如图，已知l1∥l2，直线l与l1、l2相交于C、D两点，把一块含30°角的三角尺按如图位置摆放．若∠1＝130°，则∠2＝．16．如图1是我们常用的折叠式小刀，图2中刀柄外形是一个矩形挖去一个小半圆，其中刀片的两条边缘线可看成两条平行的线段，转动刀片时会形成如图2所示的∠1与∠2，则∠1与∠2的度数和是度．三．解答题（共6小题）17．如图：已知AB∥DE∥CF，若∠ABC＝70°，∠CDE＝130°，求∠BCD的度数．18．如图，MN∥BC，BD⊥DC，∠1＝∠2＝60°．（1）AB与DE平行吗？请说明理由；（2）若DC是∠NDE的平分线．①试说明∠ABC＝∠C；②试说明BD是∠ABC的平分线．19．如图所示，已知AB∥CD，分别探讨下面四个图形中，∠APC，∠P AB与∠PCD的关系．20．如图所示，直线a∥b，AC丄AB，AC交直线b于点C，∠1＝60°，求∠2的度数．21．如图，∠BAP+∠APD＝180°，∠1＝∠2，求证：∠E＝∠F．22．如图，已知AB∥ED，∠C＝90°，∠ABC＝∠DEF，∠D＝130°，∠F＝100°，求∠E的大小．参考答案一．选择题1．解：∵AB∥EC，∴∠A＝∠ACE，∠B＝∠ECD．故选：B．2．解：如图所示，与∠1相等的角有∠B、∠DEF、∠EFC共3个，故选：C．3．解：∵直线m∥n，∴∠2＝∠ABC+∠1＝30°+20°＝50°，故选：D．4．解：∵CD∥AB，∠ACD＝40°，∴∠A＝∠ACD＝40°，∵在△ABC中，∠ACB＝90°，∴∠B＝90°﹣∠A＝50°．故选：B．5．解：∵a∥b，∴∠1＝∠3，∵∠1＝55°，∴∠3＝55°，又∵∠2＝∠3，∴∠2＝55°，故选：A．6．解：∵∠AGE＝32°，∴∠DGE＝148°，由折叠可得，∠DGH＝∠DGE＝74°，∵AD∥BC，∴∠GHC＝180°﹣∠DGH＝106°，故选：D．7．解：∵∠1＝70°，∠1与∠3是对顶角，∴∠3＝∠1＝70°．∵a∥b，点C在直线b上，∠DCB＝90°，∴∠2+∠DCB+∠3＝180°，∴∠2＝180°﹣∠3﹣∠DCB＝180°﹣70°﹣90°＝20°．故选：A．8．解：如图：过B作直线b平行于拐弯之前的道路a，由平行线的传递性得a∥b∥c，∵a∥b，∴∠A＝∠1＝66°，∵b∥c，∴∠2＝180°﹣∠C＝180°﹣153°＝27°，∴∠ABC＝∠1+∠2＝66°+27°＝93°．故选：B．9．解：根据题意，得AE∥BF，AM∥CN；∠A＝63°，∠FBC＝27°．∵AE∥BF，∴∠1＝∠A＝63°．∵AM∥CN，∴∠DCN＝∠DBM＝∠1+∠FBC＝63°+27°＝90°．故选：C．10．解：方法1：如图，∵∠1＝47°，∠4＝45°，∴∠3＝∠1+∠4＝92°，∵矩形对边平行，∴∠5＝∠3＝92°，∵∠6＝45°，∴∠2＝180°﹣45°﹣92°＝43°．方法2：如图，作矩形两边的平行线，∵矩形对边平行，∴∠3＝∠1＝47°，∵∠3+∠4＝90°，∴∠4＝90°﹣47°＝43°∴∠2＝∠4＝43°．故选：B．二．填空题11．解：∠ABC＝180°﹣∠ABE＝180°﹣150°＝30．∵AB∥CD，∴∠BCD＝∠ABC＝30°．∵CE平分∠ACD，∴∠ACD＝2∠BCD＝60°．∴∠A＝180°﹣∠ACD＝180°﹣60°＝120°．故答案为：120°．12．解：过点C作CH∥AB∴∠GCH＝∠ABC＝107°∴∠HCD+∠CDE＝180°∴∠HCD＝180°﹣130°＝50°∴∠GCD＝∠GCH﹣∠HCD＝107°﹣50°＝57°∴∠FCG＝90°﹣57°＝33°．故答案为33°．13．解：∵直线a∥b，∠1＝45°，∴∠3＝45°，∴∠2＝180°﹣45°＝135°．故答案为：135°．14．解：∵∠1＝55°，∠A＝60°，∴∠3＝∠4＝65°，∵a∥b，∴∠4+∠2＝180°，∴∠2＝115°．故答案为：115°．15．解：∵∠1＝130°，∴∠3＝50°，又∵l1∥l2，∴∠BDC＝50°，又∵∠ADB＝30°，∴∠2＝20°，故答案为：20°．16．解：如图2，AB∥CD，∠AEC＝90°，作EF∥AB，则EF∥CD，所以∠1＝∠AEF，∠2＝∠CEF，所以∠1+∠2＝∠AEF+∠CEF＝∠AEC＝90°．故答案为90．三．解答题17．解：∵AB∥CF，∠ABC＝70°，∴∠BCF＝∠ABC＝70°，又∵DE∥CF，∠CDE＝130°，∴∠DCF+∠CDE＝180°，∴∠DCF＝50°，∴∠BCD＝∠BCF﹣∠DCF＝70°﹣50°＝20°．18．解：（1）AB∥DE，理由如下：∵MN∥BC，（已知）∴∠ABC＝∠1＝60°．（两直线平行，内错角相等）又∵∠1＝∠2，（已知）∴∠ABC＝∠2．（等量代换）∴AB∥DE．（同位角相等，两直线平行）；（2）①∵MN∥BC，∴∠NDE+∠2＝180°，∴∠NDE＝180°﹣∠2＝180°﹣60°＝120°．∵DC是∠NDE的平分线，∴∠EDC＝∠NDC＝∠NDE＝60°．∵MN∥BC，∴∠C＝∠NDC＝60°．∴∠ABC＝∠C．②∠ADC＝180°﹣∠NDC＝180°﹣60°＝120°，∵BD⊥DC，∴∠BDC＝90°．∴∠ADB＝∠ADC﹣∠BDC＝120°﹣90°＝30°．∵MN∥BC，∴∠DBC＝∠ADB＝30°．∴∠ABD＝∠DBC＝∠ABC．∴BD是∠ABC的平分线．19．解：图1：∠APC＝∠P AB+∠PCD．理由：过点P作PE∥AB，∵AB∥CD，∴AB∥PE∥CD（平行线的传递性），∴∠1＝∠A，∠2＝∠C，∴∠APC＝∠1+∠2＝∠P AB+∠PCD，即∠APC＝∠P AB+∠PCD；图2：∠APC+∠P AB+∠PCD＝360°．理由：过点P作PE∥AB．∵AB∥CD，∴AB∥PE∥CD（平行线的传递性），∴∠A+∠1＝180°，∠2+∠C＝180°，∴∠A+∠1+∠2+∠C＝360°，∴∠APC+∠P AB+∠PCD＝360°；图3：∠APC＝∠PCD﹣∠P AB．理由：延长DC交AP于点E．∵AB∥CD，∴∠1＝∠P AB（两直线平行，同位角相等）；又∵∠PCD＝∠1+∠APC，∴∠APC＝∠PCD﹣∠P AB；图4：∴∠P AB＝∠APC+∠PCD．理由：∵AB∥CD，∴∠1＝∠P AB（两直线平行，内错角相等）；又∵∠1＝∠APC+∠PCD，∴∠P AB＝∠APC+∠PCD．20．解：∵AC丄AB，∴∠BAC＝90°，∵∠1＝60°，∴∠B＝180°﹣∠1﹣∠BAC＝30°，∵a∥b，∴∠2＝∠B＝30°．21．证明：∵∠BAP+∠APD＝180°（已知），∴AB∥CD（同旁内角互补，两直线平行）．∴∠BAP＝∠APC（两直线平行，内错角相等）．又∵∠1＝∠2（已知），∴∠FP A＝∠EAP，∴AE∥PF（内错角相等，两直线平行）．∴∠E＝∠F（两直线平行，内错角相等）．22．解：延长DC、AB交于G，∵ED∥AB，∠D＝130°，∴∠G＝50°，又∵∠BCD＝90°，∠BCD＝∠G+∠CBG，∴∠CBG＝40°，∴∠ABC＝140°，∴∠E＝∠ABC＝140°．。

初二数学平行线的性质定理同步练习题答案平行线的性质定理同步练习题第1题.命题“线段垂直平分线上的点到这条线段两个端点的间隔相等”.的逆命题是
.
答案：如果一个点到线段两个端点的间隔相等，那么这个点在这条线段的垂直平分线上.
第2题.以下命题中的逆命题正确的选项是( )
A.如果a=b，那么a2=b2
B.对顶角相等
C.假设三角形中有一个角是钝角，那么其余两个角都是锐角
D.线段垂直平分线上的点到这条线段的两个端点间隔相等
答案：D.
第3题.以下说法正确的选项是( )
A.在同一平面内两条直线被第三条直线所截，同旁内角互补
B.如果一个角的两边分别平行于另一个角的两边，那么这两个角一定相等
C.两个相等的角一组边平行，那么另一组边也平行
D.一条直线垂直于平行线中的一条，也一定垂直于另一条
答案：D.。

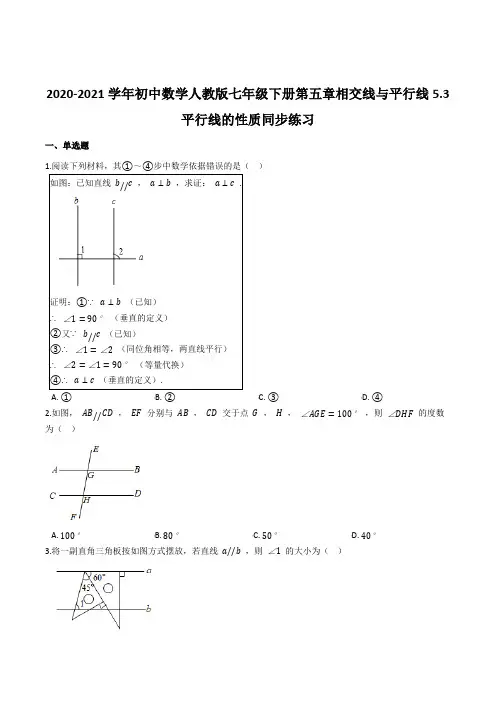
2020-2021学年初中数学人教版七年级下册第五章相交线与平行线5.3平行线的性质同步练习一、单选题1.阅读下列材料，其①～④步中数学依据错误的是（）如图：已知直线b//c，a⊥b，求证：a⊥c.证明：①∵a⊥b（已知）∴∠1=90°（垂直的定义）②又∵b//c（已知）③∴∠1=∠2（同位角相等，两直线平行）∴∠2=∠1=90°（等量代换）④∴a⊥c（垂直的定义）.A. ①B. ②C. ③D. ④2.如图，AB//CD，EF分别与AB，CD交于点G，H，∠AGE=100°，则∠DHF的度数为（）A. 100°B. 80°C. 50°D. 40°3.将一副直角三角板按如图方式摆放，若直线a//b，则∠1的大小为（）A. 45°B. 60°C. 75°D. 105°4.某同学的作业如下框，其中※处填的依据是（）.A. 两直线平行，内错角相等B. 内错角相等，两直线平行C. 两直线平行，同位角相等D. 两直线平行，同旁内角互补5.一副三角板按如图方式放置，含45°角的三角板的斜边与含30°角的三角板的长直角边平行，则∠α的度数是（）A. 10°B. 15°C. 20°D. 25°6.如图，已知AB//CD，∠A=140°，∠E=120°，则∠C的度数是（）A. 80°B. 120°C. 100°D. 140°7.如图，AB//CD，点E在BC上，DE=EC，若∠B=35°，则∠BED=（）A. 70°B. 145°C. 110°D. 140°8.如图，将一副三角板和一张对边平行的纸条按下列方式摆放，两个三角板的一直角边重合，含30°角的直角三角板的斜边与纸条一边重合，含45°角的三角板的一个顶点在纸条的另一边上，则∠1的度数是（）A. 14°B. 15°C. 20°D. 30°9.如图，∠1=80°，∠2=80°，∠5=70°，则∠3的大小是( )A. 70°B. 80°C. 100°D. 110°10.如图，l1∥l2，点O在直线l1上，将三角板的直角顶点放在点O处，三角板的两条直角边与l2交于A，B两点，若∠1＝35°，则∠2的度数为（）A. 35°B. 45°C. 55°D. 65°11.已知AB//CD，CE平分∠ACD，交AB于点E，∠A=124°，则∠1的度数为（）A. 56°B. 38°C. 36°D. 28°12.如图，已知直线AB∥CD，∠GEB的平分线EF交CD于点F，∠1＝40°，则∠2等于（）A. 130°B. 140°C. 150°D. 160°二、填空题13.下图是可调躺椅示意图（数据如图）， AE 与 BD 的交点为 C ，且 ∠A ， ∠B ， ∠E 保持不变．为了舒适，需调整 ∠D 的大小，使 ∠EFD =110° ，则图中 ∠D 应________（填“增加”或“减少”）________度．14.如图，已知等腰梯形 ABCD 中， AD//BC,BC =3AD ，如果 BC ⃗⃗⃗⃗⃗ =a ,BD⃗⃗⃗⃗⃗⃗ =b ⃗ ，那么 AB ⃗⃗⃗⃗⃗ = ________．15.如图， AC//BD,∠C =72°,∠ABC =70° ，那么 ∠ABD 的度数为________．16.如图，直线l 1∥l 2 ， ∠BAE ＝125°，∠ABF ＝85°，则∠1＋∠2=________．17.实验证明，平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等，如图，一束光线m 射到平面镜a 上，被a 反射到平面镜b 上，又被b 反射，如果被b 反射出的光线n 与光线m 平行，且 ∠1=37° ，那么 ∠2 的度数为________．18.完成下面的证明：已知：如图，∠AEC=∠A+∠C．求证：AB∥CD．证明：过点E作EF∥AB．∴∠A=▲（）．∵∠AEC=∠1+∠2,∠AEC=∠A+∠C，∴∠C=∠2．∴▲∥▲（）．∴AB∥CD（）．三、综合题19. 如图所示,AD∥BC,∠1=78°,∠2=40°,求∠ADC的度数。

7.5 平行线的性质（第2课时）一、选择题1．同一平面内的三条直线满足a⊥b，b⊥c，则下列式子成立的是（）A．a//c B．a//b C．b//c D．a⊥c2．下面推理正确的是（）A．∵a//b，b//c，∴c//d B．∵a//c，b//d，∴c//dC．∵a//b，a//c，∴b//c D．∵a//b，c//d，∴a//c3．如图，已知∠1=60°，如果CD//BE，那么∠B的度数为（）A．70°B．100°C．110°D．120°4．如图，∠1=72°，∠2=72°，∠3=70°，求∠4的度数为（）A．72°B．70°C．108°D.110°5.如图，下列推理错误的是（）A．∵∠1＝∠2，∴a//bB．∵b//c，∴∠2＝∠4C．∵a//b，b//c，∴a//cD．∵∠2+∠3＝180°，∴a//c6．如图，直线a,b及木条c在同一平面上，将木条c绕点O旋转到与直线a平行时，其最小旋转角为（）A．100°B．90°C．80°D．70°7．如图，直线a//b，∠1=∠2，∠3=150°，则∠4等于（）A．60°B．40°C．50°D．30°8．如图，如果∠1=∠3，∠2=60°，那么∠4的度数为（）A．60°B．100°C．120°D．130°9．如图，已知∠1＝70°，∠2＝110°，∠3＝95°，那么∠4＝（）A．80°B．85°C．95°D．100°10．如图，∠1=∠2，∠D=50°，则∠B的度数为（）A．50°B．40°C．100°D．130°11．如图，∠1=75°，∠2=75°，∠3=112°，则∠5−∠4的度数是（）A．68°B．44°C．180°D．34°12．如图，下列推理正确的是（）A．∵AB//CD，∴∠B=∠DCE（两直线平行，同位角相等）B．∵∠1=∠2，∴AD//BC（内错角相等，两直线平行）C．∵AD//BC，∴∠3=∠4（内错角相等，两直线平行）D．∵∠B+∠BCD=180°，∴AD//BC（同旁内角互补，两直线平行）二、填空题13．如图，直线a//c，∠1=∠2，那么直线b，c的位置关系是________．14．如图，直线a、b被c所截，a⊥l于M，b⊥l于N，∠1=66°，则∠2=________．15．如图，直线AB，CD相交于点E，DF//AB．若∠AEC=100°，则∠D等于________．三、综合题16．如图：已知∠2+∠D=180°，∠1=∠B，试说明：AB//EF．17．如图，已知∠A=∠C，∠E=∠F，试说明AB//CD．18．如图所示，若AB//CD，且∠1=∠2，试判断AM与CN位置关系，并说明理由．参考答案一、选择题1．A【解析】∵a⊥b，b⊥c，如图所示，∴∠1=∠2=90°，∴a//c．故选A．2．C【解析】A．a,c都和b平行，应该推出的是a//c，而非c//d，故错误；B．没有两条直线都和第三条直线平行，所以推不出平行，故错误；C．b,c都和a平行，可推出是b//c，故正确；D．a,c与不同的直线平行，无法推出两者也平行．故选C．3．D【解析】∵∠1=60°，∴∠2=180°−60°=120°．∵CD//BE，∴∠2=∠B=120°．故选D．4．D【解析】∠1=72°，∠2=72°，∴∠1=∠2，∴a//b，∵∠3=70°，∴∠4=180°−∠3=110°．故选D．5．D【解析】A．∵∠1＝∠2，∴a//b，正确；B．∵b//c，∴∠2＝∠4，正确；C．∵a//b，b//c，∴a//c，正确；D．∵∠2+∠3＝180°，∴a//c，错误．故选D．6．C【解析】如图，∵旋转后c'//a，∴∠1=50°，∴旋转角=180°−50°−40°=90°．故选B．7．D【解析】如图，∵直线a//b，∠3=150°，∴∠1=∠4，∠5=∠3=150°，∴∠2=180°−∠5=30°，∵∠1=2，∴∠4=2=30°．故选D．8．C【解析】∵∠1=∠3，∴a//b，∴∠5=∠2=60°，∴∠4=180°−60°=120°，故选C．9．B【解析】∵∠2＝110°，∴∠CNF＝∠2＝110°，∵∠1＝70°，∴∠1+∠CNF＝180°，∴AB//EF，∴∠3+∠4＝180°，∵∠3＝95°，∴∠4＝85°．故选B．10．D【解析】∵∠1=∠2，∠1=∠3，∴∠2=∠3，∴AB//CD，∴∠B+∠D=180°，∵∠D=50°，∴∠B=180°−∠D=130°．故选D．11．B【解析】∵∠1=75°，∠2=75°，∴∠1=∠2，∴a//b（内错角相等，两直线平行），∴∠3+∠4=180°（两直线平行，同旁内角互补）．又∵∠3=112°，∴∠4=180°−112°=68°，∠5=∠3=112°（两直线平行，同位角相等），∴∠5−∠4=112°−68°=44°．故选B．12．A【解析】∵AB//CD，∴∠B=∠DCE（两直线平行，同位角相等），选项A正确；∵∠1=∠2，∴AB//CD（内错角相等，两直线平行），选项B错误；∵AD//BC，∴∠3=∠4（两直线平行，内错角相等），选项C错误；∵∠B+∠BCD=180°，∴AB//CD（同旁内角互补，两直线平行），选项D错误．故选A．二、填空题13．b//c【解析】∵∠1=∠2，∴a//b，∵a//c，∴b//c．故答案为：b//c．14．114°【解析】∵a⊥l于M，b⊥l于N，∴a//b，∵∠1=66°，∴∠3=∠1=66°，∴∠2=180°−∠3=180°−66°=114°．15．80°【解析】∵∠CEA=100°，∴∠CEB=180°−∠CEA=80°；又∵AB//DF，∴∠CEB=∠D=80°；故答案为：80°．三、综合题16．∵∠2+∠D=180°，∴EF∥DC．（同旁内角互补，两直线平行）∵∠1=∠B，∴AB ∥DC．（同位角相等，两直线平行）∴AB∥EF．（平行于同一条直线的两条直线平行）【解析】∵∠2+∠D=180°，∴EF∥DC．（同旁内角互补，两直线平行）∵∠1=∠B，∴AB∥DC．（同位角相等，两直线平行）∴AB∥EF．（平行于同一条直线的两条直线平行）17．∵∠E=∠F，∴AE∥CF，∵∠A=∠ABF，∴∠A=∠C，∴∠ABF=∠C，∴AB∥CD．【解析】∵∠E=∠F，∴AE∥CF，∵∠A=∠ABF，∴∠A=∠C，∴∠ABF=∠C，∴AB ∥CD．18．AM//CN．证明：∵AB//CD，∴∠EAB=∠ECD；又∵∠1=∠2，而∠EAM=∠EAB−∠1，∠ACN=∠ACD−∠2，即∠EAM=∠ACN，∴AM//CN（同位角相等，两直线平行）．【解析】AM//CN．证明：∵AB//CD，∴∠EAB=∠ECD；又∵∠1=∠2，而∠EAM=∠EAB−∠1，∠ACN=∠ACD−∠2，即∠EAM=∠ACN，∴AM//CN（同位角相等，两直线平行）．。

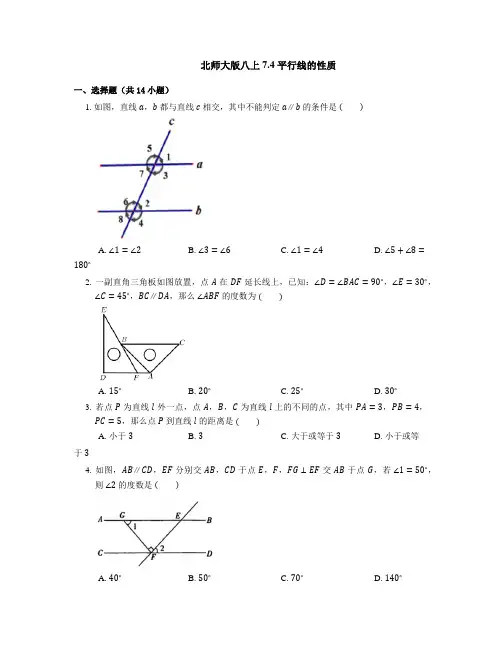
北师大版八上 7.4 平行线的性质一、选择题（共14小题）1. 如图，直线a，b都与直线c相交，其中不能判定a∥b的条件是( )A. ∠1=∠2B. ∠3=∠6C. ∠1=∠4D. ∠5+∠8= 180∘2. 一副直角三角板如图放置，点A在DF延长线上，已知：∠D=∠BAC=90∘，∠E=30∘，∠C=45∘，BC∥DA，那么∠ABF的度数为( )A. 15∘B. 20∘C. 25∘D. 30∘3. 若点P为直线l外一点，点A，B，C为直线l上的不同的点，其中PA=3，PB=4，PC=5，那么点P到直线l的距离是( )A. 小于3B. 3C. 大于或等于3D. 小于或等于34. 如图，AB∥CD，EF分别交AB，CD于点E，F，FG⊥EF交AB于点G，若∠1=50∘，则∠2的度数是( )A. 40∘B. 50∘C. 70∘D. 140∘5. 如图，直线a∥b，若∠1=40∘，∠2=55∘，则∠3等于( )A. 85∘B. 95∘C. 105∘D. 115∘6. 如图，CD∥AB，点O在AB上，OE平分∠BOD，OF⊥OE，∠D=110∘，则∠AOF的度数是( )A. 20∘B. 25∘C. 30∘D. 35∘7. 如图，AB∥EF，∠C=90∘，则α，β，γ的关系是( )A. β+γ−α=90∘B. α+β+γ=180∘C. α+β−γ=90∘D. β=α+γ8. 如图，∠1与∠2是同位角的是( )A. ②③B. ①②③C. ②③④D. ③④9. 如图，AF是∠BAC的平分线，EF∥AC交AB于点E，若∠1=35∘，则∠BEF的度数为( )A. 35∘B. 60∘C. 70∘D. 80∘10. 如图，如果AB∥CD，那么角α，β，γ之间的关系式为( )A. α+β+γ=360∘B. α−β+γ=180∘C. α+β+γ=180∘D. α+β−γ=180∘11. 如图，AB∥CD，则∠α，∠β，∠γ之间的关系为( )A. ∠α+∠β+∠γ=360∘B. ∠α−∠β+∠γ=180∘C. ∠α+∠β−∠γ=180∘D. ∠α+∠β+∠γ=180∘12. 如图，已知∠A=80∘，DB，DC分别是△ABC的外角∠EBC和∠FCB的角平分线，则∠D的度数为( )A. 50∘B. 60∘C. 70∘D. 80∘13. 如图，直线AB∥CD，CD∥EF，则AB与EF的位置关系是( )A. 平行B. 相交C. 垂直D. 不能确定14. 如图，直线AB∥CD，AE⊥CE，∠1=125∘，则∠C等于( )A. 35∘B. 45∘C. 50∘D. 55∘二、填空题（共9小题）15. 如图，在同一平面内，有三条直线a，b，c，且a∥b，如果直线a与c交于点O，那么直线c与b的位置关系是．16. 分别过点P，Q作直线b∥a，直线c∥a，则b与c的位置关系为．17. 如图，直线l1∥l2，∠1=20∘，则∠2+∠3=．18. 如图，△ABC是一块直角三角板，∠BAC=90∘，∠B=30∘．现将三角板叠放在一把直尺上，使得点A落在直尺的一边上，AB与直尺的另一边交于点D，BC与直尺的两边分别交于点E，F．若∠CAF=20∘，则∠BED的度数为∘．19. 如图，AB∥CD∥EF，那么∠BAC+∠ACE+∠CEF=度．20. 如图，AB∥CD，AB⊥AE，∠CAE=42∘，则∠ACD的度数为．21. 学习了平行线后，小敏想出了过已知直线外一点画这条直线的平行线的一种方法，她是通过折一张半透明的纸得到的．从图中可知（如图（1）∼（4）所示），小敏画平行线的依据有．（填序号）．①两直线平行，同位角相等；②两直线平行，内错角相等；③同位角相等，两直线平行；④内错角相等，两直线平行．22. 如图，AB∥DE，∠B=30∘，∠C=110∘，∠D=．23. 如图，若l1∥l2，∠1=66∘，则∠2=．三、解答题（共6小题）24. 如图，OP，OQ分别是∠AOB，∠BOC的平分线，根据所给条件并结合图形，先猜测∠POQ与∠AOC之间的数量关系，然后逐步填空．∠POQ与∠AOC之间的数量关系是：．因为OP是∠AOB的，所以∠POB=1．2．同理，∠BOQ=12于是∠POQ=( )+( )=12( )+12( )=12( + )=12( ).25. 如图，已知：点 P 在直线 CD 上，∠BAP +∠APD =180∘，∠1=∠2．求证：∠E =∠F ．26. 如图，已知 ∠AOB 内部有三条射线，OE 平分 ∠BOC ，OF 平分 ∠AOC ．（1）若 ∠AOB =90∘，∠AOC =30∘，求 ∠EOF 的度数；（2）若 ∠AOB =α，求 ∠EOF 的度数；（3）若将条件中“OE 平分 ∠BOC ，OF 平分 ∠AOC ”改为“∠EOB =13∠COB ，∠COF =23∠COA ”，且 ∠AOB =α，求 ∠EOF 的度数．27. 如图，已知：AB ∥CD ，∠PMQ =2∠QMB ，∠PNQ =2∠QND ，请判断 ∠P 与 ∠Q 的数量关系，并证明．28. 如图，EF∥AD，AD∥BC，CE平分∠BCF，∠DAC=110∘，∠ACF=20∘，求∠FEC的度数．29. 如图，已知AB∥CD∥EF∥GH．（1）如图1，M是直线EF上的点，写出∠BAM、∠AMC和∠MCD的数量关系，并证明你的结论；（2）如图2，M是直线EF上的点，写出∠BAM、∠AMC和∠MCD的数量关系，并证明你的结论；（3）如图3，点M，N分别是直线EF，GH上的动点，四个角∠BAM，∠AMN，∠MNC，∠NCD之间的数量关系有种．（不要证明）答案1. C2. A【解析】∵∠D=∠BAC=90∘，∠C=45∘，∠E=30∘，∴∠ABC=45∘，∠DFE=60∘，且BC∥AD，∴∠FAB=∠ABC=45∘，∴∠ABF=∠DFE−∠FAB=60∘−45∘=15∘．3. D4. A【解析】∵AB∥CD，∠1=50∘，∴∠CFG=∠1=50∘，∵FG⊥EF，∠CFG+∠GFE+∠2=180∘，∴∠2=180∘−90∘−50∘=40∘．5. B6. D【解析】∵CD∥AB，∠D=110∘，∴∠AOD+∠D=180∘，∠DOB=∠D=110∘，∴∠AOD=180∘−∠D=180∘−110∘=70∘，∵OE平分∠BOD，∴∠DOE=55∘，∵OF⊥OE，∴∠FOE=90∘，∴∠DOF=∠FOE−∠DOE=90∘−55∘=35∘，∴∠AOF=∠AOD−∠DOF=70∘−35∘=35∘．7. C8. B【解析】由同位角的定义可知题图①②③中∠1与∠2的位置关系是同位角．9. C【解析】∵EF∥AC，∠1=35∘，∴∠FAC=∠1=35∘，∠BEF=∠BAC，∵AF是∠BAC的平分线，∴∠BAC=2∠FAC=70∘．∴∠BEF=70∘．10. D【解析】过点E作EF∥AB，∵AB∥CD，∴EF∥AB∥CD，∴α+∠1=180∘，∠2=γ，∴β=∠1+∠2=180∘−α+γ，∴α+β−γ=180∘．11. C12. A【解析】∵BD，CD分别是∠EBC和∠FCB的平分线，∴∠CBD=12∠CBE，∠BCD=12∠BCF，∴∠CBD+∠BCD=12∠CBE+12∠BCF=12(∠CBE+∠BCF)=12(∠A+∠ACB+∠A+∠ABC)=12(180∘+∠A),∴∠D=180∘−(∠CBD+∠BCD) =180∘−12(180∘+∠A)=90∘−12∠A=90∘−12×80∘=50∘,故选：A．13. A【解析】根据平行于同一直线的两直线平行即可得出答案．14. A【解析】如图过点E作MN∥AB．∵MN∥AB，∴∠AEN=∠1=125∘，∴∠AEM=180∘−∠AEN=55∘．又∵AE⊥CE，∴∠AEC=90∘，∴∠MEC=∠AEC−∠AEM=90∘−55∘=35∘．又∵AB∥CD，MN∥AB，∴MN∥CD，∴∠C=∠MEC=35∘．15. 相交【解析】∵a∥b，又直线a与c相交，∴直线c与b的位置关系是相交．16. b∥c17. 200∘18. 8019. 360【解析】∵AB∥CD，∴∠BAC+∠ACD=180∘，∵EF∥CD，∴∠DCE+∠CEF=180∘，∴∠BAC+∠ACE+∠CEF=360∘．20. 132∘【解析】∵AB∥CD，∴∠ACD+∠BAC=180∘，∵AB⊥AE，∠CAE=42∘，∴∠BAC=90∘−∠CAE=48∘．∴∠ACD=180∘−∠BAC=132∘．21. ③④22. 100∘23. 114∘【解析】∵l1∥l2，∴∠1+∠2=180∘，∵∠1=66∘，∴∠2=180∘−∠1=180∘−66∘=114∘．∠AOC；角平分线；∠AOB；∠BOC；∠POB；∠BOQ；∠AOB；∠BOC；∠AOB；24. ∠POQ=12∠BOC；∠AOC25. ∵∠BAP+∠APD=180∘，∴AB∥CD，∴∠BAP=∠APC．又∵∠1=∠2，∴∠BAP−∠1=∠APC−∠2，即∠EAP=∠APF，∴AE∥FP，∴∠E=∠F．26. （1）因为∠AOB=90∘，∠AOC=30∘，所以∠COB=60∘．因为OE平分∠BOC，OF平分∠AOC，所以∠FOC=15∘，∠EOC=30∘，所以∠EOF=∠EOC+∠FOC=45∘．（2）因为∠AOB=α，OE平分∠BOC，OF平分∠AOC，所以∠EOF=∠EOC+∠FOC(∠BOC+∠AOC)=12=1∠AOB2α.=12∠COB，（3）因为∠EOB=13∠COB，所以∠EOC=23所以∠EOF=∠EOC+∠FOC(∠COB+∠AOC)=23∠AOB=23α.=2327. ∠P=3∠Q．证明如下：如图，作PL∥AB交MN于L，QR∥AB交MP的延长线于R，则∠RQM=∠QMB，∵AB∥CD，∴RQ∥CD，∴∠RQN=∠QND，∴∠MQN=∠QMB+∠QND．易得AB∥CD∥PL，∴∠MPL=∠PMB，∠NPL=∠PND，∴∠MPN=∠PMB+∠PND．∵∠PMQ=2∠QMB，∠PNQ=2∠QND，∴∠PMB=3∠QMB，∠PND=3∠QND，∴∠MPN=3∠MQN．28. 因为AD∥BC，所以∠DAC+∠ACB=180∘，因为∠DAC=110∘，所以∠ACB=180∘−110∘=70∘，因为∠ACF=20∘，所以∠BCF=70∘−20∘=50∘，因为CE平分∠BCF，∠BCF=25∘，所以∠BCE=12因为EF∥AD，AD∥BC，所以EF∥BC，所以∠FEC=∠BCE=25∘．29. （1）∠AMC=∠BAM+∠MCD．∵AB∥EF，∴∠BAM=∠AME．∵EF∥CD，∴∠EMC=∠MCD，∴∠AMC=∠AME+∠EMC=∠BAM+∠MCD；（2）∠AMC+∠BAM+∠MCD=360∘．∵AB∥EF，∴∠BAM+∠AMF=180∘．∵EF∥CD，∴∠FMC+∠MCD=180∘，∴∠AMC+∠BAM+∠MCD=∠BAM+∠AMF+∠FMC+∠MCD=360∘（3）4【解析】。

5.3 平行线的性质(三)◆典型例题【例1】下列语句是不是命题.(1)画∠AOB的角平分线;(2)平面上有几个点；(3)两点之间，线段最短;(4)若a≠b，则|a|≠|b|.【解析】(1)是操作性的语句；(2)是问句；(3)、(4)是判定语句.【答案】(1)、(2)不是命题；(3)、(4)是命题.【例2】指出下列命题的题论、结论:(1)如果两条直线相交，那么它们只有一个交点.(2)两条直线被第三条直线所截，如果同旁内角互补，即这两条直线平行.(3)两条平行平行线被第三条直线所截，内错角相等.(4)若∠1=∠2，∠2=∠3，则∠1=∠3.【解析】每个命题都是由题设、结论两部分组成，题设是知事项，结论是由已知事项推出的事项，命题常写成“如果…，那么…”的形式，具有这种形式的命题中，用“如果”开始的部分是题设，用“那么”开始的部分是结论.【答案】(1)题设:两条直线相交；结论:它们只有—个交点；(2)题设:两条直线被第三条直线所截，同旁内角互补；结论:这两条直线平行.(3)因为这个命题可以改写成：“如果两条平行线被第三条直线所截，那么内错角相等”；也可以简写成“如果两直线平行，那么内错角相等”，所以可以简单说成，题设:两直线平行，结论:内错角相等.(4)题设:∠1=∠2，∠2=∠3，结论:∠1=∠3.◆课前热身1.每个命题都由____________和____________两部分组成.2.命题“对顶角相等”的题设是____________,结论________________________.◆课上作业3.命题“同位角相等”改写成“如果…，那么…”的形式是____________________________.4.请用“如果…，那么…”的形式写一个命题______________5.一个命题，如果题设成立，结论一定成立，这样的命题是_____________命题；如果题设成立，结论不成立或不一定成立，这样的命题叫_______命题(填“真”、“假”).6.以下四个命题：①一个锐角与一个钝角的和为180°；②若m不是正数，则m一定小于零；③若ab＞0，则a＞0，b＞0；④如果一个数能被2整除，那么这个数一定能被4整除.真命题有_______个.◆课下作业一、填空题7.下列语句∶①对顶角相等；②OA是∠BOC的平分线；③相等的角都是直角；④线段AB.其中不是命题的是____________________________________________.8.“垂线段最短”的题设是_____________________，结论是____________________.9.命题“a、b是有理数，若a＞b，则a2＞b2”，若结论保持不变，怎样改变条件，命题才是真命题.请你写出一种改法：_______________________________________________10.对于同一平面的三条直线a、b、c，给出以下五个结论:①a∥b;②b∥c;③a⊥b;④a∥c;⑤a⊥c以其中两个为题设，一个为结论，组成一个正确的命题______________________.二、选择题11.唐伯虎点秋香的故事家喻户晓了，现在来玩个游戏：“唐伯虎点秋香”【规则】下面有四个人，其中一个人是秋香，请你通过下面提示辨别出谁是秋香.友情提示:这四个人分别是∶春香、夏香、秋香、冬香【所给人物】A、B、C、D①A不是秋香，也不是夏香；②B不是冬香，也不是春香；③如果A不是冬香，那么C不是春香；④D既不是夏香，也不是春香；⑤C不是春香，也不是冬香若上面的命题都是真命题，问谁是秋香?A.AB.BC.CD.D12.下列命题正确的是( )A.两直线与第三条直线相交，同位角相等;B.两直线与第三条直线相交，内错角相等C.两直线平行，内错角相等;D.两直线平行，同旁内角相等三、解答题13.阅读以下两小题后作出相应的解答:(1)“同位角相等，两直线平行”，“两直线平行，同位角相等”，这两个命题的题设和结论在命题中的位置恰好对凋，我们把其中一命题叫做另一个命题的逆命题，请你写出命题“角平分线上的点到角两边的距离相等的逆命题，并指出逆命题的题设和结论；(2)根据以下语句作出图形，并写出该命题的文字叙述.已知:过直线AB上一点O任作射线OC，OM、ON分别平分∠AOC、∠BOC，则OM⊥ON.14.如图5-122，给出下列论断:(1)AB∥DC；(2)AD∥BC；(3)∠A+∠B=180°；(4)∠B+∠C=180°，以其中一个作为题设，一个作为结论，写出一个真命题.想一想，若连接BD，你能自已写出一个真命题吗?试写出—个真命题并写出推理过程.图5-122参考答案◆课下作业一、填空题7.下列语句∶①对顶角相等；②OA是∠BOC的平分线；③相等的角都是直角；④线段AB.其中不是命题的是____________________________________________.答案：④8.“垂线段最短”的题设是_____________________，结论是____________________.答案：连接直线外一点与直线上一点的所有线段中；垂线段最短9.命题“a、b是有理数，若a＞b，则a2＞b2”，若结论保持不变，怎样改变条件，命题才是真命题.请你写出一种改法：_______________________________________________答案：答案不唯一，如：a＞b＞0，|a|＞|b|等10.对于同一平面的三条直线a、b、c，给出以下五个结论:①a∥b;②b∥c;③a⊥b;④a∥c;⑤a⊥c以其中两个为题设，一个为结论，组成一个正确的命题______________________.答案：下列答案任选其一：①若a∥b，b∥c则a∥c②若a∥b，a∥c则b∥c；③若a∥c，b∥c，则a∥b④若a⊥b，a⊥c，则b∥c⑤若a⊥c,b∥c，则a⊥b;⑥若a⊥b，b∥c，则a⊥c二、选择题11.唐伯虎点秋香的故事家喻户晓了，现在来玩个游戏：“唐伯虎点秋香”【规则】下面有四个人，其中一个人是秋香，请你通过下面提示辨别出谁是秋香.友情提示:这四个人分别是∶春香、夏香、秋香、冬香【所给人物】A、B、C、D①A不是秋香，也不是夏香；②B不是冬香，也不是春香；③如果A不是冬香，那么C不是春香；④D既不是夏香，也不是春香；⑤C不是春香，也不是冬香若上面的命题都是真命题，问谁是秋香?A.AB.BC.CD.D答案：D12.下列命题正确的是( )A.两直线与第三条直线相交，同位角相等;B.两直线与第三条直线相交，内错角相等C.两直线平行，内错角相等;D.两直线平行，同旁内角相等答案：C三、解答题13.阅读以下两小题后作出相应的解答:(1)“同位角相等，两直线平行”，“两直线平行，同位角相等”，这两个命题的题设和结论在命题中的位置恰好对凋，我们把其中一命题叫做另一个命题的逆命题，请你写出命题“角平分线上的点到角两边的距离相等的逆命题，并指出逆命题的题设和结论；(2)根据以下语句作出图形，并写出该命题的文字叙述.已知:过直线AB上一点O任作射线OC，OM、ON分别平分∠AOC、∠BOC，则OM⊥ON.答案：(1)到角两边距离相等的点在这个角的平分线上；题设是到角两边距离相等的点，结论是该点在这个角的平分线上(2)图略；邻补角的平分线互相垂直14.如图5-122，给出下列论断:图5-122(2)AB∥DC；(2)AD∥BC；(3)∠A+∠B=180°；(4)∠B+∠C=180°，以其中一个作为题设，一个作为结论，写出一个真命题.想一想，若连接BD，你能自已写出一个真命题吗?试写出—个真命题并写出推理过程.答案：(1)(4)、(2)(3)、(4)(1)、(3)(2)中任选一个；AD∥BC则∠ADB=∠CBD或∠ADB=∠CBD则AD∥BC.略。

七年级数学下册７.5．1 平行线的性质同步练习(新版)冀教版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望（七年级数学下册7.5.1 平行线的性质同步练习（新版）冀教版)的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为七年级数学下册7．5．1 平行线的性质同步练习（新版）冀教版的全部内容。

7.5.１平行线的性质基础训练1。

如图,直线l1∥l2，直线ｌ３与l1、l2分别交于A、Ｂ两点,若∠１=70°,则∠2=（）A.70°B.8０°ﻩC。

１１0°Ｄ。

120°2.如图,AD是∠EAC的平分线，ＡD∥BＣ,∠B=3０°，则∠Ｃ为（）A。

60°B．８０° C.1２0° D.3０°3。

如图,已知∠１=∠2，∠BAD=42°,则∠B=____＿_＿__＿＿_＿．4。

如图,已知AB∥CＤ,直线MN分别交ＡB，CＤ于Ｅ，F,∠MFＤ=5０°,ＥＧ平分∠ＭＥB，那么∠MＥG的大小是 .5.已知:如图，AB∥DC，AD∥BE,试说明：∠ABE＝∠D.培优提升１.将直尺和直角三角板按如图方式摆放,已知∠1=３0°,则∠2的大小是（)A。

30°B。

4５°Ｃ。

60°ﻩD。

６５°2.如图，AB∥ＣＤ∥EF,AＣ∥DＦ,若∠A=120°，则∠Ｄ等于（)A。

60°ﻩB.120°C。

１５０° D.180°3.下列说法中正确的是( ）A.两直线被第三条直线所截得的同位角相等Ｂ。

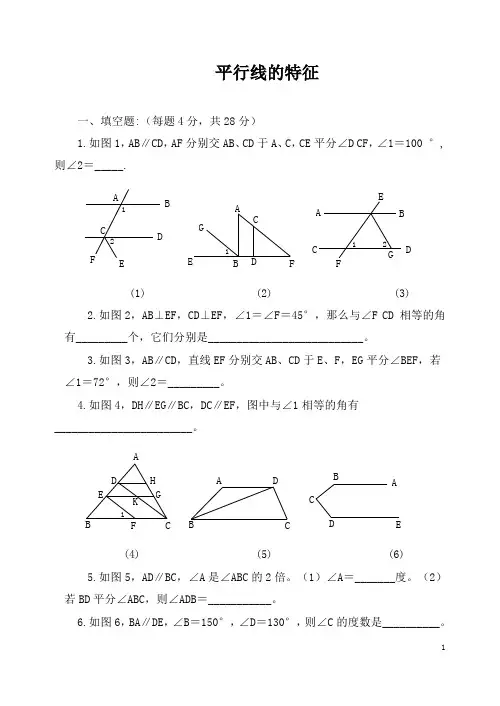
平行线的特征一、填空题:（每题4分，共28分）1.如图1，AB ∥CD ，AF 分别交AB 、CD 于A 、C ，CE 平分∠D CF ，∠1＝100 °,则∠2＝_____.21FE DCB AG 1F ECBAG21EDCB A(1) (2) (3) 2.如图2，AB ⊥EF ，CD ⊥EF ，∠1＝∠F ＝45°，那么与∠F CD 相等的角有_________个，它们分别是___________________________。

3.如图3，AB ∥CD ，直线EF 分别交AB 、CD 于E 、F ，EG 平分∠BEF ，若∠1＝72°，则∠2＝_________。

4.如图4，DH ∥EG ∥BC ，DC ∥EF ，图中与∠1相等的角有________________________。

K HG 1FED CA DCBA ED C B A(4) (5) (6) 5.如图5，AD ∥BC ，∠A 是∠ABC 的2倍。

（1）∠A ＝_______度。

（2）若BD 平分∠ABC ，则∠ADB ＝___________。

6.如图6，BA ∥DE ，∠B ＝150°，∠D ＝130°，则∠C 的度数是__________。

7.如图7，∠ACD ＝∠BCD ，DE ∥BC 交AC 于E ，若∠ACB ＝6 0°，∠B ＝74°，则∠EDC ＝___°，∠CDB ＝____°。

E D C B A FEDCBA30︒北西南东B AγβαDCBA(7) (8) (9)(10)二、选择题:（每题4分，共28分）8.如图8，由AC ∥ED ，可知相等的角有（ ） A.6对 B.5对 C.4对 D.3对 9.如图9，由A 到B 的方向是（ ）A.南偏东30°B.南偏东60°C.北偏西30°D.北偏西60°10.如图10，如果AB ∥CD ，则角α、β、γ之间的关系为（ ） A. α+β+γ＝360° B. α-β+γ＝180° C. α+β-γ＝180° D. α+β+γ＝180°11.如图11，AB ∥CD ∥EF ，若∠ABC ＝50°，∠CEF ＝150°，则∠BCE ＝（ ）A.60°B.50°C.30°D.20°F EDCB A FEDCBA(11) (12) 12.下列说法中，为平行线特征的是（ ）①两条直线平行, 同旁内角互补; ②同位角相等, 两条直线平行;③内错角相等, 两条直线平行; ④垂直于同一条直线的两条直线平行. A.① B.②③ C.④ D.②和④13.如果两个角的一边在同一直线上，另一边互相平行，那么这两个角只能（ ）A.相等B.互补C.相等或互补D.相等且互补14.如图12，AB ⊥BC ，BC ⊥CD ，∠EBC ＝∠BCF ，那么，∠ABE 与∠DCF 的位置与大小关系是 （ ）A.是同位角且相等;B.不是同位角但相等;C.是同位角但不等;D.不是同位角也不等三、解答题:（共44分）15.已知，如图，MN ⊥AB ，垂足为G ，MN ⊥CD ，垂足为H ，直线EF 分别交AB 、CD 于G 、Q ，∠GQC ＝120°，求∠EGB 和∠HGQ 的度数。

平行线的特征同步练习练习平行线是具有以下特征的直线：1.直线上的任意两点与一条已知直线上的任意两点的连线的夹角相等。

2.直线与已知直线的夹角为90度（垂直于已知直线）。

3.直线与已知平面的平行线的直线也是与该平面垂直的直线（垂直于平行于该平面的两条直线）。

4.两个垂直于同一条直线的直线是垂直的。

下面是一些用来练习平行线特征的例题：例题1：已知直线l1与平面P1垂直，且直线l2与l1平行，证明直线l2与平面P1垂直。

证明：由题意，直线l1与平面P1垂直，即l1垂直于P1，而l2与l1平行，即l2也平行于P1、根据平行线的特征3，l2也与P1垂直，所以l2与平面P1垂直。

例题2：已知直线AB与直线CD平行，直线EF与直线CD垂直，证明直线EF与直线AB垂直。

证明：由题意，直线CD与直线AB平行，即CD∥AB，而直线EF与直线CD垂直，即EF⊥CD。

根据平行线的特征4，EF也与AB垂直，所以EF与直线AB垂直。

例题3：已知直线AB与直线CD平行，直线EF与直线AB垂直，证明直线EF与直线CD垂直。

证明：由题意，直线AB与直线CD平行，即AB∥CD，而直线EF与直线AB垂直，即EF⊥AB。

根据平行线的特征1，EF与CD的垂线也是垂直的，所以EF与直线CD垂直。

例题4：已知直线l1与平面P1平行，直线l2与l1垂直，证明直线l2与平面P1垂直。

证明：由题意，直线l1与平面P1平行，即l1∥P1，而直线l2与l1垂直，即l2⊥l1、根据平行线的特征3，直线l2与P1的垂线也是垂直的，所以l2与平面P1垂直。

通过以上例题的练习，可以巩固平行线特征的应用和推理能力。

同时，理解平行线的特征也有助于解决几何问题和证明。

继续多做类似的练习题，对平行线的特征有更深入的理解和掌握。

《5．3.1 平行线的性质》教案第1课时平行线的性质【教学目标】1．理解平行线的性质；(重点)2．能运用平行线的性质进行推理证明．(重点、难点)【教学过程】一、情境导入窗户内窗的两条竖直的边是平行的，在推动过程中，两条竖直的边与窗户外框形成的两个角∠1、∠2有什么数量关系？二、合作探究探究点一：平行线的性质如图，AB∥CD，BE∥DF，∠B＝65°，求∠D的度数．解析：利用“两直线平行，内错角相等，同旁内角互补”的性质可求出结论．解：∵AB∥CD，∴∠BED＝∠B＝65°.∵BE∥FD，∴∠BED＋∠D＝180°，∴∠D＝180°－∠BED＝180°－65°＝115°.方法总结：已知平行线求角度，应根据平行线的性质得出同位角相等，内错角相等，同旁内角互补．再结合已知条件进行转化．探究点二：平行线与角平分线的综合运用如图，DB∥FG∥EC，∠ACE＝36°，AP平分∠BAC，∠PAG＝12°，求∠ABD 的度数．解析：先利用GF ∥CE ，易求∠CAG ，而∠PAG ＝12°，可求得∠PAC ＝48°.由AP 是∠BAC 的角平分线，可求得∠BAP ＝48°，从而可求得∠BAG ＝∠BAP ＋∠PAG ＝48°＋12°＝60°，即可求得∠ABD 的度数．解：∵FG ∥EC ，∴∠CAG ＝∠ACE ＝36°.∴∠PAC ＝∠CAG ＋∠PAG ＝36°＋12°＝48°.∵AP 平分∠BAC ，∴∠BAP ＝∠PAC ＝48°.∵DB ∥FG ，∴∠ABD ＝∠BAG ＝∠BAP ＋∠PAG ＝48°＋12°＝60°.方法总结：(1)利用平行线的性质可以得出角之间的相等或互补关系，利用角平分线的定义，可以得出角之间的倍分关系；(2)求角的度数，可把一个角转化为一个与它相等的角或转化为已知角的和差．探究点三：平行线性质的探究应用如图，已知∠ABC .请你再画一个∠DEF ，使DE ∥AB ，EF ∥BC ，且DE 交BC 边与点P .探究：∠ABC 与∠DEF 有怎样的数量关系？并说明理由．解析：先根据题意画出图形，再根据平行线的性质进行解答即可．解：∠ABC 与∠DEF 的数量关系是相等或互补．理由如下：如图①，因为DE ∥AB ，所以∠ABC ＝∠DPC .又因为EF ∥BC ，所以∠DEF ＝∠DPC ，所以∠ABC ＝∠DEF .如图②，因为DE ∥AB ，所以∠ABC ＋∠DPB ＝180°.又因为EF ∥BC ，所以∠DEF ＝∠DPB ，所以∠ABC ＋∠DEF ＝180°.故∠ABC 与∠DEF 的数量关系是相等或互补．方法总结：画出满足条件的图形时，必须注意分情况讨论，即把所有满足条件的图形都要作出来．三、板书设计平行线的性质⎩⎨⎧⎭⎬⎫两直线平行，同位角相等两直线平行，内错角相等两直线平行，同旁内角互补求角的大小或说明角之间的数量关系【教学反思】平行线的性质是几何证明的基础，教学中注意基本的推理格式的书写，培养学生的逻辑思维能力，鼓励学生勇于尝试．在课堂上，力求体现学生的主体地位，把课堂交给学生，让学生在动口、动手、动脑中学数学第2课时平行线的性质和判定及其综合运用【教学目标】1．掌握平行线的性质与判定的综合运用；(重点、难点)2．体会平行线的性质与判定的区别与联系．【教学过程】一、复习引入问题：平行线的判定与平行线的性质的区别是什么？判定是已知角的关系得平行关系，性质是已知平行关系得角的关系．两者的条件和结论刚好相反，也就是说平行线的判定与性质是互逆的．二、合作探究探究点一：先用判定再用性质如图，C，D是直线AB上两点，∠1＋∠2＝180°，DE平分∠CDF，EF ∥AB.(1)CE与DF平行吗？为什么？(2)若∠DCE＝130°，求∠DEF的度数．解析：(1)由∠1＋∠DCE＝180°，∠1＋∠2＝180°，可得∠2＝∠DCE，即可证明CE∥DF；(2)由平行线的性质，可得∠CDF＝50°.由DE平分∠CDF，可得∠CDE＝1 2∠CDF＝25°.最后根据“两直线平行，内错角相等”，可得到∠DEF的度数．解：(1)CE∥DF.理由如下：∵∠1＋∠2＝180°，∠1＋∠DCE＝180°，∴∠2＝∠DCE，∴CE∥DF；(2)∵CE∥DF，∠DCE＝130°，∴∠CDF＝180°－∠DCE＝180°－130°＝50°.∵DE平分∠CDF，∴∠CDE＝12∠CDF＝25°.∵EF∥AB，∴∠DEF＝∠CDE＝25°.方法总结：根据题目中的数量找出各量之间的关系是解这类问题的关键．从角的关系得到直线平行用平行线的判定，从平行线得到角相等或互补的关系用平行线的性质，二者不要混淆．探究点二：先用性质再用判定如图，已知DF∥AC，∠C＝∠D，CE与BD有怎样的位置关系？说明理由．解析：由图可知∠ABD和∠ACE是同位角，只要证得同位角相等，则CE∥BD.由平行线的性质结合已知条件，稍作转化即可得到∠ABD＝∠C.解：CE∥BD.理由如下：∵DF∥AC，∴∠D＝∠ABD.∵∠C＝∠D，∴∠ABD＝∠C，∴CE∥BD.方法总结：解答此类要判定两直线平行的题，可围绕截线找同位角、内错角和同旁内角．探究点三：平行线性质与判定中的探究型问题如图，AB∥CD，E，F分别是AB，CD之间的两点，且∠BAF＝2∠EAF，∠CDF＝2∠EDF.(1)判定∠BAE，∠CDE与∠AED之间的数量关系，并说明理由；(2)∠AFD与∠AED之间有怎样的数量关系？解析：平行线中的拐点问题，通常需过拐点作平行线．解：(1)∠AED＝∠BAE＋∠CDE.理由如下：如图，过点E作EG∥AB.∵AB∥CD，∴AB∥EG∥CD，∴∠AEG＝∠BAE，∠DEG＝∠CDE.∵∠AED＝∠AEG＋∠DEG，∴∠AED＝∠BAE＋∠CDE；(2)同(1)可得∠AFD ＝∠BAF ＋∠CDF .∵∠BAF ＝2∠EAF ，∠CDF ＝2∠EDF ，∴∠BAE ＋∠CDE ＝32∠BAF ＋32∠CDF ＝32(∠BAF ＋∠CDF )＝32∠AFD ，∴∠AED ＝32∠AFD .方法总结：无论平行线中的何种问题，都可转化到基本模型中去解决，把复杂的问题分解到简单模型中，问题便迎刃而解．三、板书设计⎭⎬⎫同位角相等内错角相等同旁内角互补判定性质两直线平行【教学反思】本节内容的重点是平行线的性质及判定的综合，直接运用了“∵”“∴”的推理形式，为学生创设了一个学习推理的环境，逐步培养学生的逻辑推理能力．因此，这一节课有着承上启下的作用，比较重要．本节内容的难点是理解平行线的性质和判定的区别，并在推理中正确地应用．由于学生还没有学习命题的概念和命题的组成，不知道判定和性质的本质区别和联系是什么，所以在教学中，应让学生通过应用和讨论，体会到如果已知角的关系，推出两直线平行，就是平行线的判定；反之，如果两直线平行，得出角的关系，就是平行线的性质《5.3.1 平行线的性质》导学案第1课时 平行线的性质【学习目标】：1.掌握两直线平行，同位角、内错角相等，同旁内角互补，并能熟练运用.2.通过独立思考，小组合作，运用猜想、推理的方法，提升自己利用图形分析问题的能力.3.激情投入，全力以赴，培养严谨细致的学习习惯.【重点】：平行线的性质.【难点】：根据平行线的性质进行推理.【自主学习】一、知识链接平行线的判定方法有哪几种？二、新知预习如图，直线a与直线b平行，直线c与它们相交.（1）量一量：用量角器量图中8个角的度数.（2）说一说：由测量的结果，你发现∠1与∠5、∠2与∠6、∠3与∠7、∠4与∠8、∠3与∠6、∠4与∠5、∠3与∠5、∠4与∠6的大小有什么关系？（3）想一想：（2）中的各对角分别是什么角？（4）议一议：两条平行直线被第三条直线所截，所得的同位角、内错角、同旁内角有什么关系？三、自学自测1.如图，直线a∥b，∠1=70°，那么∠2的度数是（）A.50°B.60°C.70°D.80°2.下列说法中，（1）同位角相等，两直线平行；（2）两直线平行，同旁内角互补；（3）内错角相等，两直线平行；（4）同一平面内，垂直于同一直线的两条直线平行.其中是平行线的性质的是（）A.（1）和（3）B.（2）C.（4）D.（2）和（4）【课堂探究】要点探究探究点：平行线的性质问题1：画两条平行线a//b，然后画一条截线c与a、b相交，标出如图所示的角. 度量所形成的8个角的度数，把结果填入下表：角∠1 ∠2 ∠3 ∠4度数角∠5 ∠6 ∠7 ∠8度数观察：∠1~ ∠8中，哪些是同位角？它们的度数之间有什么关系？说出你的猜想.猜想：两条平行线被第三条直线所截，同位角 .思考：再任意画一条截线d，同样度量各个角的度数，你的猜想还成立吗？问题2：如图，已知a//b,那么∠2与∠3相等吗？为什么?问题3：如图,已知a//b,那么∠2与∠4有什么关系呢？为什么?例1.如图是一块梯形铁片的残余部分，量得∠A=100°，∠B=115°，梯形的另外两个角的度数分别是多少？例2：小明在纸上画了一个∠A，准备用量角器测量它的度数时，因不小心将纸片撕破，只剩下如图的一部分，如果不能延长DC、FE的话，你能帮他设计出多少种方法测出∠A的度数？【当堂检测】1.如图，已知平行线AB、CD被直线AE所截(1)从∠1=110°可以知道∠2 是多少度吗,为什么？(2)从∠1=110°可以知道∠3是多少度吗,为什么？(3)从∠1=110°可以知道∠4 是多少度吗,为什么？2.如图，一条公路两次拐弯的前后两条路互相平行.第一次拐弯时∠B是142°，第二次拐弯时∠C是多少度？为什么？3.如图，直线 a ∥ b,直线b垂直于直线c，那么直线a垂直于直线c吗?4.如果有两条直线被第三条直线所截，那么必定有（）A.内错角相等B.同位角相等C.同旁内角互补D.以上都不对5.(1)如图1,若AB∥DE , AC∥DF，试说明∠A=∠D.请补全下面的解答过程,括号内填写依据.解: ∵ AB∥DE( )∴∠A=_______ ( )∵AC∥DF( )∴∠D=______ ( )∴∠A=∠D ( )(2)如图2,若AB∥DE , AC∥DF，试说明∠A+∠D=180o.请补全下面的解答过程,括号内填写依据.解: ∵ AB∥DE( )∴∠A= ______ ( )∵AC∥DF( )∴∠D+ _______=180° ( )∴∠A+∠D=180°（）6.【拓展题】如图，潜望镜中的两面镜子是互相平行放置的，光线经过镜子反射时，∠1=∠2，∠3=∠4，∠2和∠3有什么关系？为什么进入潜望镜的光线和离开潜望镜的光线是平行的？5.3.1 平行线的性质第2课时平行线的性质和判定及其综合运用【学习目标】：1.进一步熟悉平行线的判定方法和性质.2.运用平行线的性质和判定进行简单的推理和计算.【重点】：平行线的判定方法和性质.【难点】：平行线的性质和判定的综合运用.【自主学习】一、知识链接1.平行线的判定方法有哪些？2.平行线的性质有哪些？二、新知预习1.两条直线被第三条直线所截，同位角、内错角相等，或者说同旁内角互补，这句话对吗？2.自主归纳：（1）两直线平行，同位角，内错角，同旁内角 .（2）不难发现，平行线的判定，反过来就是，注意它们之间的联系和区别.（3）运用平行线的性质时，不要忽略前提条件“”，不要一提同位角或内错角，就认为是相等的.【课堂探究】一、要点探究探究点：平行线的性质和判定及其综合应用例1.如图，三角形ABC中，D是AB上一点，E是AC上一点，∠ADE=60°，∠B = 60°，∠AED=40°.（1）DE和BC平行吗？为什么？（2）∠C是多少度？为什么？做一做：已知AB∥CD，∠1 = ∠2.试说明:BE∥CF.例2.如图，AB∥CD，猜想∠A、∠P 、∠PCD的数量关系，并说明理由.例3.如图，若AB//CD ，你能确定∠B 、∠D 与∠BED 的大小关系吗？说说你的看法．【变式题1】如图，AB//CD ，探索∠B 、∠D 与∠DEB 的大小关系 .【变式题2】如图,AB ∥CD,则∠A ，∠C 与∠E 1，∠E 2，…，∠E n 有什么关系？【变式题3】如图,若AB ∥CD, 则∠A ，∠C 与各拐角之间有什么关系？EDC BA【当堂检测】1.填空：如图,(1)∠1= 时，AB∥CD.(2)∠3= 时，AD∥BC.2.直线a,b与直线c相交，给出下列条件：①∠1= ∠2;②∠3= ∠6;③∠4+∠7=180°;④∠3+ ∠5=180°，其中能判断a//b的是( )A. ①②③④ B .①③④ C. ①③ D. ④3. 有这样一道题：如图，AB//CD,∠A=100°, ∠C=110°,求∠AEC的度数. 请补全下列解答过程.解：过点E作EF//AB.∵AB//CD（已知）,∴ // (平行于同一直线的两直线平行）.∴∠A+∠ =180°，∠C+∠ =180°(两直线平行，同旁内角互补）.又∵∠A=100°，∠C=110°（已知）,∴∠ = °, ∠ = °.∴∠AEC=∠1+∠2= °+ ° = °.4.已知AB⊥BF，CD⊥BF，∠1= ∠2，试说明∠3=∠E.5.如图,EF∥AD，∠1=∠2，∠BAC=70 °，求∠AGD的度数.第五章相交线与平行线5.3.1《平行线的性质》同步练习一、单选题（共15题；共30分）1、如图，把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20o，那么∠2的度数是（ )A、30°B、25°C、20°D、15°2、如图所示BC//DE，∠1=108°，∠AED=75°，则∠A的大小是（）A、60°B、33°C、30°D、23°3、两条平行直线被第三条直线所截，下列命题中正确的是（）A、同位角相等，但内错角不相等B、同位角不相等，但同旁内角互补C、内错角相等，且同旁内角不互补D、同位角相等，且同旁内角互补4、一架飞机向北飞行，两次改变方向后，前进的方向与原来的航行方向平行，已知第一次向左拐50°，那么第二次向右拐（）A、40°B、50°C、130°D、150°5、如图，下列说法正确的是（）A、若AB//CD，则∠1=∠2B、若AD//BC，则∠B+∠BCD=180ºC、若∠1=∠2，则AD//BCD、若∠3=∠4，则AD//BC6、下列图形中，由AB//CD能得到∠1=∠2的是（）A、 B、C、 D、7、下列语句：①两条不相交的直线叫做平行线；②过直线外一点有且只有一条直线与已知直线垂直；③若AB=BC，则点B是AC的中点；④若两角的两边互相平行，则这两个角一定相等；其中说法正确的个数是（）A、1B、2C、3D、48、同一平面内，两条不重合的直线的位置关系是（）A、平行或垂直B、平行或相交C、平行、相交或垂直D、相交9、下列生活实例中；①交通道口的斑马线；②天上的彩虹；③体操的纵队；④百米跑道线；⑤火车的平直铁轨线．其中属于平行线的有（）A、1个B、2个C、3个D、4个10、如图，AB∥CD，∠A=46°，∠C=27°，则∠AEC的大小应为（）A、19°B、29°C、63°D、73°11、如图，直线l1∥l2，且分别与△ABC的两边AB、AC相交，若∠A=50°，∠1=35°，∠2的度数为（）A、95°B、65°C、85°D、35°12、如图，已知：AB∥CD，CE分别交AB、CD于点F、C，若∠E=20°，∠C=45°，则∠A的度数为（）A、5°B、15°C、25°D、35°13、如图，l∥m，矩形ABCD的顶点B在直线m上，则∠α=（）A、20°B、25°C、30°D、35°14、如图，若a∥b，则下列选项中，能直接利用“两直线平行，内错角相等”判定∠1=∠2的是（）A、 B、C、 D、15、如图，如果AB∥CD，那么图中相等的内错角是（）A、∠1与∠5，∠2与∠6B、∠3与∠7，∠4与∠8C、∠5与∠1，∠4与∠8D、∠2与∠6，∠7与∠3二、填空题（共5题；共10分）16、如图，已知：∠A=∠F，∠C=∠D，求证：BD∥EC，下面是不完整的说明过程，请将过程及其依据补充完整．证明：∵∠A=∠F（已知）∴AC∥________，________∴∠D=∠1________又∵∠C=∠D（已知）∴∠1=________________∴BD∥CE ________17、如图，点A，C，F，B在同一直线上，CD平分∠ECB，FG∥CD．若∠ECA为α度，则∠GFB为________ 度（用关于α的代数式表示）．18、如图所示,一条公路两次拐弯后和原来的方向相同,即拐弯前、•后的两条路平行,若第一次拐角是150°,则第二次拐角为________ .19、如图，把含有60 º角的三角尺ABC的直角顶点C放在直线DE上，当AB∥DE。

5.3平行线的性质课时1平行线的性质基础训练知识点1 两直线平行，同位角相等1.如图，直线a∥b,∠1=60°，则∠2=( )A.30°B.60°C.45°D.120°2.(2018新疆乌鲁木齐中考)如图，把一个直角三角尺的直角顶点放在直尺的一边上，若∠1=50°,则∠2=( )A.20°B.30°C.40°D.50°3.如图AC∥DF,AB∥EF，点D，E分别在AB，AC上，若∠2=50°，则∠1的度数为 .知识点2 两直线平行，内错角相等4.(2018四川泸州中考)如图，直线a∥b，直线c分别交a,b于点A,C,∠BAC的平分线交直线b于点D，若∠1=50°，则∠2的度数是( )A.50°B.70°C.80°D.110°5.如图，点A在直线BG上,AD∥BC，AE平分∠GAD，若∠CBA=80°,则( )A.60°B.50°C.40°D.30°6.如图，点D,E分别在AB，BC上，DE∥AC，AF∥BC，∠1=70°，则∠2= °.知识点3两直线平行，同旁内角互补7.(2018湖北仙桃中考)如图，AD∥BC，∠C =30°，∠ADB:∠BDC= 1:2，则∠DBC的度数是( )A.30°B.36°C.45°D.50°8.如图，AB∥CD∥EF，AC∥DF，若∠BAC=120°，则∠CDF=( )A.60°B.65°C.50°D.45°知识点4 平行线的判定与性质的综合运用9.如图，已知c⊥a,c⊥b，直线b，c，d交于一点，若∠1=50°，则∠2等于( )A.60°B.50°C.40°D.30°10.如图，∠1=∠2，∠3=40°，则∠4等于( )A.120°B.130°C.140°D.40°11.(2017河北唐山路北区期中)如图，已知直线AB∥DF,∠D+∠B=180°.(1)试说明DE∥BC；(2)若∠AMD=75°，求∠AGC的度数.参考答案1.B解析：∵a∥b,∴∠2=∠1,又∠1=60°，∴∠2=60°.故选B2.C解析：如图，∵直尺的对边互相平行，∴∠3=∠1=50°,又∠3+90°+∠2=180°,∴∠2= 180°-50°-90°=40°.故选 C.名师点睛：本题考查平行线的性质和平角的定义，熟记性质并准确识图是解题的关键.3.50°解析：因为AB∥EF，所以∠A=∠2=50°.因为AC∥DF,所以∠1=∠A =50°.4.C解析：∵a∥b,∠1=50°,∴∠BAD=∠1=50°，∵AD平分∠BAC,∴∠BAC=2∠BAD = 100°,∴∠2=180°-∠BAC =180°-100°=80°.故选 C.5. B解析：∵AD∥BC,∠CBA=80°,∠DAB=∠CBA= 80°,∴∠DAG=180°-80°=100°.∵AE平分∠GAD,∴∠GAE=12∠DAG=50°.故选 B.6.10解析：DE∥AC,∴∠C=∠1 =70°. ∵AF∥BC,∴∠2=∠C=10°.7.D解析：∵AD∥BC,∴∠ADC+∠C=180°.又∠C=30°，∠ADC=180°-∠C=180°-30°=150°. ∵∠ADB：∠BDC=1：2,∴∠ADB+∠BDC=∠ADC=150°,∴∠ADB =13∠ADC =13×150°=50°.∵AD∥BC，∴∠DBC=∠ADB=50°.故选D8.A解析：∵AB∥CD,∴∠BAC+∠C=180°，又∠BAC=120°，∴∠C=180°-∠BAC=60°.∵AC∥DF,∠CDF =∠C=60°.故选A.9.B解析：a⊥c,b⊥c. ∴a∥b,∴∠2=∠1 =50°.故选 B.10.C解析：∵∠1=∠2,∴a∥b, ∴∠3 =∠5.∵∠3=40°,∴∠5=40°,∴∠4=180°-40°=140°.故选 C.11.解析：(1)∵AB∥DF,∴∠D+∠BHD= 180°,∵∠D+∠B=∠DHB,∴DE∥B C.(2)由（1)知DE∥BC,∴∠AGB=∠AMD=75°,∴AGC=180°-∠AGB =180°-75°= 105°.课时1平行线的性质提升训练1.(2018广东深圳中考)如图，直线a,b被c,d所截，且a∥b，则下列结论中正确的是( )A.∠1=∠2 C.∠3+∠4=180°B.∠3=∠4 D.∠1+∠4=180°2.(2018河南安阳五中课时作业)如图，小岛C在小岛A的北偏东60°方向，在小岛B的北偏西45°方向，那么从C岛看A，B两岛的视角∠ACB的度数为.3.(2018四川广安中考)一大门栏杆的平面示意图如图所示，BA垂直地面AE于点A，CD平行于地面AE，若∠BCD=150°，则∠ABC=度.4.(2018安徽芜湖二十七中课时作业)如图，AB∥DC，AC和BD相交于点O, E是CD上一点，F是OD上一点，且∠1=∠A.(1)试说明FE∥OC;(2)若∠BFE=70°，求∠DOC的度数.5.(2018天津市实验中学课时作业)如图,CD∥AB,CD∥GF,FA与AB交于点A，与CD交于点E.试说明∠4=∠1+∠C.6.(2018河北张家口五中课时作业)如图，已知∠1+∠2=180°，∠3=∠B，试判断∠AED与∠C的大小关系，并对结论进行说明.7.(2018山西朔州一中课时作业)课上老师呈现一个问题：如图，AB∥CD，EF⊥AB于点O，FG交CD于点P,当∠1=30°时，求∠EFG的度数.甲、乙、丙三位同学用不同的方法添加辅助线解决问题，如下图：甲同学辅助线的作法和分析思路如下：辅助线:过点F作MN∥CD分析思路：(1)欲求∠EFG的度数，由图可知只需求∠2和∠3的度数；(2)由MN∥CD可知，∠2=∠1，已知∠1的度数，可得∠2的度数；(3)由AB∥CD，MN∥CD推出AB∥MN，由此可推出∠3=∠4；(4)已知EF⊥AB，可得∠4=90°，所以可得∠3的度数；(5)从而可求∠EFG的度数.请你选择乙同学或丙同学所画的图形,描述辅助线的作法，并写出相应的分析思路.参考答案1.B解析：根据两直线平行，同位角相等,可得∠3=∠4故选B.2.105°解析：如图，过点C作CE∥AF,交AB于点E，则CE∥AF∥BD, ∴∠FAC=∠ACE,∠CBD=∠BCE,∴∠ACB=∠ACE+∠BCE=∠FAC+∠CBD=60°+45°=105°.3.120解析：如图，过点B作BG∥AE.∵CD∥AE,∴BG∥CD,∴∠GBC+∠BCD =180°.又∠BCD= 150°，∴∠GBC=180°-∠BCD=180o -150°=30°.∵BA⊥AE,∴∠BAE = 90°.∵BG∥AE,∴∠GBA+∠BAE =180°，∴∠GBA=180°-∠BAE =90°.∴∠ABC=∠GBA+∠GBC=90°+30°=120°.4.解析：(1)∵AB∥CD,∴∠A=∠C .又∠1=∠A,∴∠C=∠1.∴FE∥O C.(2)由(1)知FE∥OC,∴∠BFE+∠DOC =180°又∠BFE=70°,∴∠DOC =110°.5.解析：∵CD∥GF,∴∠C= ∠GF C.∵∠GFA=∠1+∠GFC,∴∠GFA=∠1+∠C.∵CD∥AB,CD∥GF,∴AB∥GF.∴∠A=∠GFA,∴∠A=∠1+∠C.6.解析：∠AED=∠C.理由如下：∵∠1+∠4=180°,∠1+∠2=180°,∴∠2=∠4.∴EF∥AB，∴∠3=∠ADE.又∠B=∠3，∴∠ADE=∠B，∴DE∥BC，∴∠AED=∠C.7.解析：选择乙同学所画的图形.辅助线:过点P作PH∥EF，交于点H.分析思路：(1)欲求∠EFG的度数，由PH∥EF可知，∠EFG=∠HPG,因此，只需求出∠HPG的度数；(2)欲求∠HPG的度数，由图可知只需求出∠1和∠2的度数；(3)已知∠1的度数,所以只需求出∠2的度数；(4)已知EF⊥AB可得∠4=90°；(5)由PH∥EF可推出∠3=∠4,由AB∥CD可推出∠2=∠3,由此可推出∠2=∠4，所以可得∠2的度数；(6)从而可求出∠EFG的度数.选择丙同学所画的图形.辅助线:过点O作交CD于点Q.分析思路：(1)欲求的度数，由OQ∥FG可知，∠EFG=∠EOQ，因此，只需求出∠EOQ的度数；(2)欲求∠EOQ的度数，由图可知只需求出∠2和∠3的度数；(3)已知EF⊥AB,可得∠3=90°；(4)由AB∥CD可推出∠2=∠4，由OQ∥FG可推出∠4 =∠1，由此可推出∠2=∠1,所以可得∠2的度数；(5)从而可求出∠EFG的度数.(选择任一种即可）。

学生做题前请先回答以下问题问题1：由角的关系得平行，可以考虑哪些定理？问题2：由平行得角的关系，可以考虑哪些定理？问题3：如图：如图，AD∥BC，AB∥CD，点E在CB的延长线上.如图：∵AD∥BC∴( )你还能得到其他的结论吗？问题4：（上接第3题）∵AB∥CD∴( )你还能得到其他的结论吗？平行线的性质、判定过程训练（推理）一、单选题(共8道，每道12分)1.已知：如图，点B在DC上，BE平分∠ABD，∠DBE=∠A求证：BE∥AC．证明：如图，∵BE平分∠ABD（已知）∴∠DBE=∠1（角平分线的定义）∵∠DBE=∠A（已知）∴∠1=∠A（____________________）∴BE∥AC（____________________）①同角或等角的余角相等；②等量代换；③内错角相等，两直线平行；④两直线平行，内错角相等．以上空缺处依次所填正确的是( )A.①④B.②③C.①③D.②④答案：B解题思路：第一个空：由∠DBE=∠A，∠DBE=∠1，推出∠1=∠A，把∠DBE代换掉了，因此依据是等量代换．第二个空：条件是∠1=∠A，结论是BE∥AC，由内错角相等得到平行，所以依据是内错角相等，两直线平行．故选B．试题难度：三颗星知识点：平行线的判定2.如图所示，∠1=∠2，AC平分∠DAB．求证：DC∥AB．证明：如图，∵AC平分∠DAB（已知）∴∠1=∠3（角平分线的定义）∵∠1=∠2（已知）∴____________（等量代换）∴DC∥AB（____________________）①∠2=∠3；②DC∥AB；③同位角相等，两直线平行；④两直线平行，内错角相等；⑤内错角相等，两直线平行．以上空缺处依次所填正确的是( )A.①⑤B.②③C.①④D.②⑤答案：A解题思路：第一个空：由∠1=∠3，∠1=∠2，利用等量代换，得到∠2=∠3．第二个空：条件是∠2=∠3，结论是DC∥AB，由内错角相等得到平行，所以这一步推理的依据是内错角相等，两直线平行．故选A．试题难度：三颗星知识点：平行线的判定3.已知：如图，直线a，b与直线c，d分别相交，∠1=∠2，∠3=110°．求∠4的度数．解：如图，∵∠1=∠2（已知）∴________（同位角相等，两直线平行）∴∠3+∠4=180°（____________________）∵∠3=110°（已知）∴∠4=70°（等式性质）①a∥b；②c∥d；③同旁内角互补，两直线平行；④两直线平行，同旁内角互补．以上空缺处依次所填正确的是( )A.①④B.②③C.①③D.②④答案：A解题思路：第一个空：∠1和∠2直线a和直线b被直线d所截得到的同位角，由同位角相等，两直线平行，得a∥b；第二个空：条件是a∥b，结论是∠3+∠4=180°，由平行得到同旁内角互补，所以这一步推理的依据是两直线平行，同旁内角互补．故选A．试题难度：三颗星知识点：平行线的性质4.如图所示，∠C+∠COE=180°，∠B+∠COE=180°．求证：AB∥CD．证明：如图，∵∠C+∠COE=180°，∠B+∠COE=180°（已知）∴∠C=∠B（同角或等角的补角相等）∴________（____________________）①AB∥OE；②AB∥CD；③CD∥OE；④两直线平行，内错角相等；⑤内错角相等，两直线平行．以上空缺处依次所填正确的是( )A.③④B.①⑤C.②④D.②⑤答案：D解题思路：条件是∠C=∠B，∠C和∠B是直线AB和直线CD被直线BC所截得到的内错角，由内错角相等，两直线平行，得AB∥CD．所以第一个空应填AB∥CD，依据是内错角相等，两直线平行．故选D．试题难度：三颗星知识点：同角的补角相等5.已知：如图，，点B，A，D在同一条直线上，AE是∠DAC的角平分线．求证：AE∥BC．证明：如图，∵AE是∠DAC的角平分线（已知）∴（角平分线的定义）∵（已知）∴∠1=∠C（____________________________）∴AE∥BC（____________________________）①内错角相等，两直线平行；②内错角相等；③两直线平行，内错角相等；④等量代换；⑤同位角相等，两直线平行．以上空缺处依次所填正确的是( )A.④③B.②③C.④①D.④⑤答案：C解题思路：第一个空：由，，推出∠1=∠C，依据是等量代换；第二个空：条件是内错角∠1=∠C，结论是AE∥BC，由条件得到结论的依据是内错角相等，两直线平行．故选C．试题难度：三颗星知识点：平行线的判定6.已知：如图，AB∥ED，∠ECF=70°．求∠BAF的度数．解：如图，∵∠ECF=70°（已知）∴∠1=_____（平角的定义）∵AB∥ED（已知）∴____________（两直线平行，同位角相等）∴∠BAF=110°（等量代换）①∠BAF；②110°；③70°；④；⑤；⑥．以上空缺处依次所填正确的是( )A.①⑥B.①⑤C.②⑤D.②④答案：D解题思路：第一个空：条件是∠ECF=70°，结合下面的推理过程以及这一步的依据是平角的定义，因此应填110°．第二个空：条件是AB∥ED，结合下面的推理过程以及这一步的依据是两直线平行，同位角相等，因此应填．故选D．试题难度：三颗星知识点：平行线的性质7.已知：如图，AB∥CD，BC∥DE．求证：∠B+∠D=180°．证明：如图，∵AB∥CD（已知）∴____________（两直线平行，内错角相等）∵BC∥DE（已知）∴____________（两直线平行，同旁内角互补）∴∠B+∠D＝180°（等量代换）①∠B=∠C；②∠B=∠E；③∠C=∠D；④∠C+∠D=180°；⑤∠D=∠E．以上空缺处依次所填正确的是( )A.①③B.②④C.①④D.②③答案：C解题思路：第一个空：条件是AB∥CD，图上平行线AB和CD只被BC所截，并结合这一步的依据是两直线平行，内错角相等，因此应填是∠B=∠C．第二个空：条件是BC∥DE，图上平行线BC和DE只被CD所截，结合这一步的依据是两直线平行，同旁内角互补，因此应该填写的是∠C+∠D=180°．故选C．试题难度：三颗星知识点：平行线的性质8.已知：如图，EF平分∠AED，∠AED=60°，∠2=30°．求证：EF∥BD．证明：如图，∵EF平分∠AED（已知）∴____________（角平分线的定义）∵∠AED=60°（已知）∴（等量代换）∵∠2=30°（已知）∴∠1=∠2（等量代换）∴____________（内错角相等，两直线平行）．①；②；③；④EF∥BD；⑤ED∥BC．以上空缺处依次所填正确的是( )A.③⑤B.②④C.①④D.②⑤答案：B解题思路：第一个空：条件是EF平分∠AED，根据下面的推理过程中以及这一步的依据：角平分线的定义，因此应填．第二个空：条件是∠1=∠2，∠1=∠2是直线EF和直线BD被直线ED所截得到的内错角，根据内错角相等，两直线平行，可得EF∥BD．故选B．试题难度：三颗星知识点：平行线的判定。

人教版 七年级数学 5.3 平行线的性质 同步训练一、选择题（本大题共10道小题） 1. 如图，直线l 1∥l 2，则∠α为()A. 150°B. 140°C. 130°D. 120°2. （2020·河南）如图， 1l ∥2l ，3l ∥4l ，若∠1=70°，则∠2的度数为( ) A.100° B.110° C.120° D.130°3. 如图，直线m n ∥，155∠=°，245∠=°则3∠的度数为（） A ．80°B ．90°C ．100°D ．110°mn1234. （2020·随州）2.如图，直线1l ∥2l ，直线l 与1l ，2l 分别交于A ，B 两点，若∠1=60°，则∠2的度数是（ ） B.60° D.100°C.120°D.140°5. 如图，AB ∥CD ，DA ⊥AC ，垂足为A ，若∠ADC ＝35°，则∠1的度数为( )A . 65°B . 55°C . 45°D . 35°6. （2020·常州）如图，直线a、b被直线c所截，a∥b，∠1＝140°，则∠2的度数是() A．30°B．40°C．50°D．60°7. 将一幅直角三角板（∠A＝∠FDE＝90°，∠F＝45°，∠C＝60°，点D在边AB上）按图中所示位置摆放，两条斜边为EF，BC，且EF//BC，则∠ADF等于（）A．70°B．75°C．80°D．85°EFAC BD8. 一个等腰直角三角尺和一把直尺按如图所示的位置摆放，若∠1＝20°，则∠2的度数是（）A．15°B．20°C．25°D．40°9. 如图，∠AOB的一边OA为平面镜，∠AOB＝37°36′，在OB上有一点E，从E点射出一束光线经OA上一点D反射，反射光线DC恰好与OB平行，则∠DEB 的度数是()A．75°36′B．75°12′C．74°36′D．74°12′10. 如图所示，两直线AB CD、平行，则l23456∠+∠+∠+∠+∠+∠=( ) A．630︒B．720︒C．800︒D．900︒65HG 4321DCFEBA二、填空题（本大题共8道小题）11. 如图，直线l与直线a，b相交．若a b∥，170∠=°，则2∠的度数是．图221bal12. 如图，已知a b∥，170∠=︒，240∠=︒，则3∠=__________．ba321CBA13. 有一直的纸带，如图折叠时，α∠=_________．α30°E DCBA14. （2020·黄冈）已知：AB∥EF，∠ABC=75°，∠CDF=135°，则∠BCD=________度．135°75°A BE FD15. （2019·上海）如图，已知直线l1∥l2，含90°角的三角板的直角顶点C在l1上，30°角的顶点A在l2上，如果边AB与l1的交点D是AB的中点，那么∠1＝度．16. （2020·恩施）如图，直线12//l l，点A在直线1l上，点B在直线2l上，AB BC=，30C ∠=︒，180∠=︒，则2∠=______．17. （2020·永州）已知直线//a b ，用一块含30°角的直角三角板按图中所示的方式放置，若125∠=︒，则2∠=_________．18. （2020·新疆）如图，若AB ∥CD ，∠A ＝110°，则∠1＝________°．三、解答题（本大题共3道小题）19. 已知如图所示，AB DE ∥,116D ∠=︒，93DCB ∠=︒，求B ∠的度数.D CEBA20. 如下图所示，已知AB CD ∥，分别探讨下面四个图形中BPD ∠与B ∠，D ∠的关系.PPPDC BA(1) (2) (3) (4)DD CC BBAA A BCD P21. 请你分析下面的题目，从中总结规律，填写在空格上，并选择一道题目具体书写证明.（1）如图⑴，已知：AB CD ∥，直线EF 分别交AB ，CD 于M ，N ，MG ，NH 分别平分AME ∠，CNE ∠.求证：MG NH ∥.从本题我能得到的结论是： . （2）如图⑵，已知：AB CD ∥，直线EF 分别交AB ，CD 于M ，N ，MG ，NH 分别平分BMF ∠， CNE ∠.求证：MG NH ∥.从本题我能得到的结论是： . （3）如图⑶，已知：AB CD ∥，直线EF 分别交AB ，CD 于M ，N ，MG ，NH 分别平分AMF ∠， CNE ∠，相交与点O .求证：MG NH ⊥. 从本题我能得到的结论是： . （4）如图⑷，已知：AB ，CD 相交于O ，OF 平分AOC ∠，OE 平分BOD ∠.求证：F ，O ，E 三点共线.从本题我能得到的结论是： .(1)A B C DE FG H M N(2)NMFEDC B A GH (3)NM FEDC B A G H O (4)A BCD E F O人教版 七年级数学 5.3 平行线的性质 同步训练-答案一、选择题（本大题共10道小题） 1. 【答案】D 【解析】α＝70°＋(180°－130°)＝120°.2. 【答案】B【解析】如图，∵直线l1∥l2，∴∠3＝∠1＝70°，∵3l ∥4l，∴∠3＋∠2＝180°，∴ ∠2＝110°．3. 【答案】C ．4. 【答案】C【解析】本题考查了平行线的性质、邻补角的性质，解答过程如下：如图所示，∵1l ∥2l ，∴∠3=∠1=60°， ∵∠2+∠3=180°，∴∠2=180°-∠3=180°-60°=120°.因此本题选C ．5. 【答案】B【解析】∵DA ⊥AC ，∠ADC ＝35°，∴∠ACD ＝90°－∠ADC ＝90°－35°＝55°，∵AB ∥CD ，∴∠1＝∠ACD ＝55°，故选B.6. 【答案】B【解析】本题考查了平行线的性质，如图，由于a ∥b ，所以∠3＝∠2，又由于∠1＋∠3＝180°，∠1＝140°，所以∠2＝40°．7. 【答案】B，【解析】本题考查平行线的性质． 解：∵EF //BC ，∴∠CGD ＝∠E ＝45°，3∵∠CGD 是△GDB 的外角，∴∠GDB ＝∠CGD －∠B ＝45°－30°＝15°． ∵∠EDF ＝90°，∴∠ADF ＝180°－15°－90°＝75°．故选B.GE F ACBD8. 【答案】C【解析】∵AB ∥CD ， ∴∠3＝∠1＝20°，∵三角形是等腰直角三角形，∴∠2＝45°﹣∠3＝25°．9. 【答案】B【解析】根据平面镜反射原理可知，∠ADC ＝∠ODE ，∵DC ∥OB ，∴∠ADC ＝∠AOE ，∴∠ODE ＝∠AOE ＝37°36′，∴∠DEB ＝∠ODE ＋∠AOE ＝37°36′＋37°36′＝75°12′，故选B.10. 【答案】D.【解析】分别过E F C H ，，，点做AB 的平行线，再求各个角度的和．选D二、填空题（本大题共8道小题） 11. 【答案】110°．12. 【答案】70︒13. 【答案】75︒【解析】∵AC BD ∥ ∴30CBE ∠=︒由折叠问题可知：ABC ABD ∠=∠∴()118030752ABD ∠=︒-︒=︒∵AC BD ∥∴75ABD α∠=∠=︒14. 【答案】30【解析】本题考查了平行线的性质，对顶角以及三角形外角等知识．如答题所示，由AB ∥EF 可得∠B+∠1=180°，而∠B=75°，则∠1=105°；有对顶角相等可得∠1=∠2=105°；由三角形的一个外角等于与它不相邻的两个内角之和，得∠2+∠C=135°，进而求出∠C=30°，因此本题答案为30．21135°75°A BEFCD15. 【答案】120【解析】∵D 是斜边AB 的中点，∴DA ＝DC ，∴∠DCA ＝∠DAC ＝30°，∴∠2＝∠DCA ＋∠DAC ＝60°，∵11∥l2，∴∠1＋∠2＝180°，∴∠1＝180°－60°＝120°．16. 【答案】40°【解析】∵AB =BC ，∠C =30︒， ∴∠CAB =30︒，∴∠CBA =120︒， ∵∠1=80︒， ∴∠EBA =40︒， ∵12//l l∴240EBA ∠∠==︒，故答案为：40︒．17. 【答案】35°【详解】如图，标注字母，延长ED 交a 于C ， 由题意得：30,90,B DEB ∠=︒∠=︒ 60,BDE ∴∠=︒//,a b 2,DCA ∴∠=∠1,125,BDE DCA ∠=∠+∠∠=︒602535,DCA ∴∠=︒-︒=︒235.∴∠=︒故答案为：35.︒18. 【答案】70【解析】本题考查了平行线的性质以及对顶角的性质．如答图，因为AB ∥CD ，所以∠A ＋∠2＝180°，所以∠2＝180°－∠A ＝180°－110°＝70°．因为∠1＝∠2，所以∠1＝70°．三、解答题（本大题共3道小题）19. 【答案】29︒【解析】过点C 作直线CF AB ∥，因为AB DE ∥,所以AB DE CF ∥∥，DCFEBA因为116D ∠=︒，18011664DCF ∠=︒︒=︒-因为93C ∠=︒，所以936429BCF ∠=︒-︒=︒， 因为B BCF ∠=∠，所以29B ∠=︒．20. 【答案】过P 做AB 、CD 的平行线，即可得如下结论： ⑴360BPD B D ∠+∠+∠= ； ⑵BPD D B ∠=∠-∠ ； ⑶BPD B D ∠=∠+∠ ； ⑷BPD B D ∠=∠-∠ .21. 【答案】（1） 两直线平行，同位角的角平分线平行. （2）证明：∵AB ∥CD ，∴BMF CNE ∠=∠ 又∵MG ，NH 分别平分BMF ∠，CNE ∠∴1122GMF BMF CNE HNM ∠=∠=∠=∠，∴MG ∥NH从本题我能得到的结论是： 两直线平行，内错角的角平分线平行. （3）证明：∵AB ∥CD ，∴180AMF CNE ∠+∠= 又∵MG ，NH 分别平分AMF ∠，CNE ∠∴119022GMF HNE AMF CNE ∠+∠=∠+∠=∴18090MON GMF HNE ∠=-∠-∠=，∴MG ⊥NH从本题我能得到的结论是： 两直线平行，同旁内角的角平分线垂直. （4）证明：∵AB ，CD 相交于O ，∴AOC BOD ∠=∠ ∵OF 平分AOC ∠，OE 平分BOD ∠∴12AOF AOC ∠=∠，12DOE BOD ∠=∠∵180AOC AOD ∠+∠=，∴180AOF AOD DOE ∠+∠+∠=即F ，O ，E 三点共线从本题我能得到的结论是： 对顶角的平分线，在一条直线上. 要证明三点共线 ，我们可以通过证明这三点所成的角为180.。

1 质简单的几何图形推理学案06-平行线的性质同步练习07一、填空1．如图1，已知∠1 = 100°，AB∥CD，则∠2 = ，∠3 = ，∠4 = ．2．如图2，直线AB 、CD 被EF 所截，若∠1 =∠2，则∠AEF +∠CFE = ．3．如图3所示（1）若EF∥AC，则∠A +∠ = 180°，∠F + ∠ = 180°（ ）．（2）若∠2 =∠ ，则AE∥BF．（3）若∠A +∠ = 180°，则AE∥BF．4．如图4，AB∥CD，∠2 = 2∠1，则∠2 = ．5．如图5，AB∥CD，EG⊥AB 于G ，∠1 = 50°，则∠E = ．6．如图6，直线l 1∥l 2，AB⊥l 1于O ，BC 与l 2交于E ，∠1 = 43°，则∠2 = ．7．如图7，AB∥CD，AC⊥BC，图中与∠CAB 互余的角有 ．8．如图8，AB∥EF∥CD，EG∥BD，则图中与∠1相等的角（不包括∠1）共有 个．二、解答下列各题9．如图9，已知∠ABE +∠DEB = 180°，∠1 =∠2，求证：∠F =∠G．10．如图10，DE∥BC，∠D∶∠DBC = 2∶1，∠1 =∠2，求∠DEB 的度数．图1 2 4 3 1 A B C D E 1 2 A B D C E F 图2 1 2 3 4 5 A B C D F E 图3 1 2 A B C D E F 图4 图51 A B C D E F G H 图7 12 D A C B l 1 l 2 图8 1 A F C D E G 图6 C D F E B A 图9 1 2 A C B F G E D 图102 1 B CE D211．如图11，已知AB∥CD，试再添上一个条件，使∠1 =∠2成立．（要求给出两个以上答案，并选择其中一个加以证明）12．如图12，∠ABD 和∠BDC 的平分线交于E ，BE 交CD 于点F ，∠1 +∠2 = 90°．求证：（1）AB∥CD； （2）∠2 +∠3 = 90°．图11 12 A B E F D C C 图12 1 2 3A B DF。

7.4 平行线的性质一、选择题1．已知D AOB ,40︒=∠是OA 上的一点，作OB DE OA CD //,⊥，那么=∠CDE （ ） A ．50° B ．130° C ．50°或130° D ．100°2．如图，EF DC BC EG DH //,////，则与1∠相等的角的个数为（ ）A ．2B ．3C ．4D ．53．如图，已知︒=∠90,//C EF AB ，那么z y x ,,的关系是（ ）A ．z x y +=B ．︒=++180z y xC ．︒=-+90z y xD ．︒=-+90x z y二、填空题1．如图，︒=∠∠=∠1201,42，则____3=∠．2．如图，DE BC CD AB //,//，则____=∠+∠D B 度．3．如图，CD BC DE ,//是ACB ∠的角平分线，︒=∠50ACB ，则____=∠EDC 度．三、解答题1．如图，已知：直线︒=∠1151,//,//d c b a ，求32∠∠、的度数．2．如图，已知：d c b a 、,//都是b a 、的截线，432,705,801∠∠∠︒=∠︒=∠、、各是多少度？为什么？3．如图，A 、B 、C 、D 在一条直线上，EF AD //． （1）︒=∠58E 时，21∠∠、各等于多少度？为什么？ （2）︒=∠78F 时，43∠∠、各等于多少度？为什么？4．如图，CD 平分︒=∠∠80,//,AED BC DE ACB ，那么DCB ∠等于多少度？为什么？5．如图，已知C EBF DHF AGE ∠=∠∠=∠,． 求证：ADC A ∠=∠．6．如图，已知CM ED AB ,//平分CN CM BCE ⊥∠,．求证：DCN B ∠=∠2．7．已知：如图，FC HG AC FG BCF ACF //,//,∠=∠．求证：BGH FGH ∠=∠．参考答案一、选择题 1．C 2．C 3．C二、填空题1．120° 2．180° 3．25° 三、解答题1．︒=∠︒=∠1153,11522．︒=∠︒=∠︒=∠1104,1103,8023．（1）︒=∠︒=∠1222,581 （2）︒=∠︒=∠784,1023 4．BC DE // （已知），∴ACB AED ∠=∠（两直线平行同位角相等） ︒=∠80AED （已知）， ∴︒=∠80ACB ．CD 平分ACB ∠（已知）， ∴BCD ACD ∠=∠， ∴︒=∠40DCB ．4．DBF AGE ∠=∠ ，又BHG DHF CGH AGE ∠=∠∠=∠, ，∴BHG CGH ∠=∠，根据内错角相等，两直线平行可得BF EC //， ∴EBF AEC ∠=∠， 又C EBF ∠=∠ ，∴C AEC ∠=∠，根据内错角相等，两直线平行可得CD AB //， ∴ADC A ∠=∠． 5．CN CM ⊥ ，∴︒=∠+∠︒=∠+∠90,90NCD MCE NCB MCB ．CM 平分BCE ∠， ∴ECM BCM ∠=∠． ∴NCD NCB ∠=∠． ED AB // ， ∴BCD B ∠=∠． ∴DCN B ∠=∠2．7．提示：由AC FG //，得C G F A C F ∠=∠．由FC HG //，得F G H C F G ∠=∠且BCF BGH ∠=∠．所以BCF BGH ACF FGH ∠=∠∠=∠,．而BCF ACF ∠=∠，所以BGH FGH ∠=∠．。

7.7.3平行线的性质1.如图所示，AB⊥EF，CD⊥EF，∠1=∠F=45°，那么与∠FCD相等的角有 ( )A.1个B.2个C．3个 D．4个2.如图所示，CD∥OB，EF∥OA.推理填空：因为CD∥OB(已知)，所以∠1=∠2( )．因为EF∥OA(已知)，所以∠O=∠2( )．所以∠O=∠1（等量代换）．因为∠1+∠3=180°( )，所以∠O+∠3=180°( )．因为∠1=∠4( )，所以∠O=∠4( )．因为∠5=∠3( )，所以∠O+∠5=180°( )．3．同时______两条平行线，并且夹在这两条平行线间的______________叫做这两条平行线的距离．4．已知：如图，DE∥AB．请根据已知条件进行推理，分别得出结论，并在括号内注明理由．(1)∵DE∥AB，( )∴∠2＝______．(__________，__________)(2)∵DE∥AB，( )∴∠3＝______．(__________，__________)(3)∵DE∥AB( )，∴∠1＋______＝180°．(______，______)5．已知：如图，∠1＋∠2＝180°．求证：∠3＝∠4．证明思路分析：欲证∠3＝∠4，只要证______∥______．证明：∵∠1＋∠2＝180°，( )∴______∥______．(__________，__________)∴∠3＝∠4．(______，______)6．已知：如图，AB∥CD，∠1＝∠2．求证：BE∥CF．证明思路分析：欲证BE∥CF，只要证______＝______．证明：∵AB∥CD，( )∴∠ABC＝______．(____________，____________)∵∠1＝∠2，( )∴∠ABC－∠1＝______－______，( )即_____＝______．∴BE∥CF．(__________，__________)7．已知：如图，四边形ABCD中，AB∥CD，AD∥BC，∠B＝50°．求∠D的度数．分析：可利用∠DCE作为中间量过渡．解法1：∵AB∥CD，∠B＝50°，( )∴∠DCE＝∠_______＝______°．(____________，______)又∵AD∥BC，( )∴∠D＝∠______＝_______°．(____________，__________)想一想：如果以∠A作为中间量，如何求解?解法2：∵AD∥BC，∠B＝50°，( )∴∠A＋∠B＝______．(____________，____________)即∠A＝______－______＝______°－______°＝______°．∵DC∥AB，( )∴∠D＋∠A＝______．(_____________，_____________)即∠D＝______－______＝______°－______°＝______°．8．已知：如图，AB∥CD，AP平分∠BAC，CP平分∠AC D，求∠APC的度数．解：过P点作PM∥AB交AC于点M．∵AB∥CD，( )∴∠BAC ＋∠______＝180°．( ) ∵PM ∥AB ，∴∠1＝∠_______，( )且PM ∥_______．(平行于同一直线的两直线也互相平行) ∴∠3＝∠______．(两直线平行，内错角相等) ∵AP 平分∠BAC ，CP 平分∠ACD ，( )∠=∠∴211______，∠=∠214______．( ) 90212141=∠+∠=∠+∠∴ACD BAC ．( )∴∠APC ＝∠2＋∠3＝∠1＋∠4＝90°．( ) 总结：两直线平行时，同旁内角的角平分线______．9.如图所示，AB ∥CD,AC ⊥BC ，图中与∠CAB 互余的角有几个？10．如图，某县电信公司在由东向西埋设通信电缆，他们从点A 埋到点B 时突然发现前方是一个具有研究价值的古墓葬群，不得不改变方向绕开古墓葬群，结果改为南偏西44°方向埋设到点C 处，再沿古墓葬群边缘埋设到点D 处，测得∠BCD=65°，现要恢复原来的正西方向DE ，则∠CDE 应等于多少度？11．如图，DE ∥BC ，∠D ∶∠DBC ＝2∶1，∠1＝∠2，求∠E 的度数．12．如图，AB ∥DE ，∠1＝25°，∠2＝110°，求∠BCD 的度数．参考答案1.D解析：与∠FCD相等的角有∠1、∠F、∠ABG、∠BAF，共4个.2.两直线平行，内错角相等两直线平行，同位角相等平角的定义等量代换对顶角相等等量代换对顶角相等等量代换3．垂直于，线段的长度．4．(1)已知，∠5，两直线平行，内错角相等．(2)已知，∠B，两直线平行，同位角相等．(3)已知，∠2，两直线平行，同旁内角互补．5～8 略9.解：图中与∠CAB互余的角有3个：∠ABC、∠3、∠2．10.解：如图,作两条与南北方向平行的直线，∴∠1=∠2，∠3=∠4．∵∠1= 44°，∠2+∠3=65°，∴∠2=44°，∠3=21°，∴∠4=21°.∵∠CDE=90°+∠4，∴∠CDE=111°.11．30°．12．95°．。