光纤光栅应变测试实验
- 格式:pdf
- 大小:522.96 KB
- 文档页数:8






实验二 光纤光栅动态应变测试实验一、实验目的当简支梁受外载荷情况下,学会用光纤光栅传感器测量其表面某点的应变,加深对光纤光栅动态应变测试的理解。
在实验过程中采集数据,分析并处理数据,并做时域分析。
二、实验设备WS-ZHT2型振动综合教学实验台光纤光栅解调仪光纤光栅焊接机光纤布拉格光栅(FBG )三、实验原理在材料力学中,由梁弯曲变形的基本公式得:zy =I M σ (1) 矩形截面,惯性矩3z b h I =12(2) 由胡克定律可知:=E σε (3)注:45号钢弹性模量E=209Gpa应力应变引起光栅布拉格波长漂移可以由下式给予描述:()Δεk ΔεPe 1λεΔλεB B =-= (4)式中,Pe 为光纤的弹光系数,εk 为应变ε引起的波长变化的灵敏度系数。
对于带有中心反射波长B λ, 的典型的石英光纤,轴向应变ε和波长漂移B Δλ有如下关系:B Δλ/B λ=0.78ε (5)说明:1nm=103pm 1pm ≈1με四、实验内容与步骤1 测量出简支梁的长宽高以及所测点在的位置,根据公式(1)、(2)、(3),给出在激励F 作用下所测点对应的应变该变量ε,即F 与ε的关系。
2 在静载荷下采集波长,求得波长的平均值0λ3 在同一频率下分别施加F1、F2、F3,分别采集所对应的波长13λλλ、2、,求出波长变化量13λλλ∆∆∆、2、(0=-λλλ∆),然后分别代入(5)式中计算得应变13εεε、2、 3 每一实验小组分别选三个频率,分别在每个频率下施加F1、F2、F3,通过采样、计算后得到应变13εεε、2、。
4 绘出时域上的应变图,进行频谱分析,观察频谱图中频率大小是否与实验中所给频率大小相同,分析时域图中应变变化与力的变化的关系,从而判断实验与理论是否吻合。
五、实验报告要求1 从理论上推导外载荷F 与应变ε之间的关系2 先在静态下求出波长平均值0λ,通过加外载荷实验得到的波长λ,算出变化量λ∆,再转化成应变ε,用EXCEL 或MATLAB 绘制时域图,并分析图形走势3 频谱分析,试着从频谱上观察振动频率,振动幅值。


光纤光栅应变传感器二维应变测量方法作者:李金娟来源:《无线互联科技》2015年第02期摘要:文章介绍了光纤光栅二维应力传感测量的试验台的准备、光纤光栅的制备、光纤光栅的粘贴、实验仪器、实验过程、光纤光栅测量应变与电阻应变片的测量结果作对比。
实验结果说明利用光纤光栅应变花可以得出与电阻应变花一致的结果。
关键词:光纤光栅;电阻应变片;应变;直角应变花光纤光栅应变花进行二维平面应力测量是通过三个光纤光栅的中心波长的变化来测定应变的,电阻应变片应变花测出的应变值对光纤光栅中心波长进行标定。
所以粘贴时尽可能保证光纤光栅与对应的电阻应变片的测量方位一致。
1 实验台的准备由于本实验需要用多个光纤光栅进行二维应力测量,所以不能使用一般的等强度梁,而是用一个十字架形结构,实际上也是一种等强度梁,不过这种装置有两个等强度梁,分别作为十字架的X轴向和Y轴向,用来施加压力,如图1所示。
这是实验的被测表面的俯视图,表面是由我们用一块马口铁皮做成的。
实验时在X轴、Y 轴方向分别悬挂砝码盘。
砝码的重力通过试验台的等悬梁臂结构拉伸X或者Y方向的铁皮,铁皮的应力的变化引起光纤光栅中心波长的变化,因此为了保证试验的效果,光纤光栅的粘贴必须使光栅光纤紧贴被测表面时同时发生应变。
2 光纤光栅的制备实验台准备好后重要的是制备光纤光栅,本实验使用3只不同中心波长的光纤光栅,串联成直角应变花来测试动态应力的变化,因而需制备3只不同波长的光纤光栅。
由于实验条件的限制,试验室中只有两块相位掩模板,在实验室中只能制备两只光纤光栅,另外一只光纤光栅是已经制备好的光纤光栅。
三只光纤光栅的波长位置分别在:1532nm,1544nm,1548nm处附近。
根据实验条件,组建一个光纤光栅制作系统,制作方法采用目前最有效,也是最流行的相位掩模法,其实验系统如图2所示。
本实验用光纤,是载氢掺锗光敏光纤-普通光纤经过载氢处理(在室温下,压强为107Pa 的容器中,载氢两周左右),使得普通通信光纤的光敏性大大增加,达到写制光栅的要求。
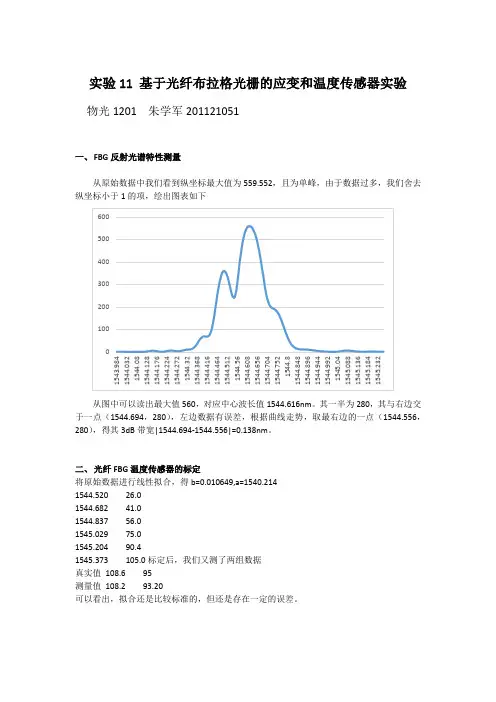
实验11基于光纤布拉格光栅的应变和温度传感器实验物光1201 朱学军201121051一、FBG反射光谱特性测量从原始数据中我们看到纵坐标最大值为559.552,且为单峰,由于数据过多,我们舍去纵坐标小于1的项,绘出图表如下从图中可以读出最大值560,对应中心波长值1544.616nm。
其一半为280,其与右边交于一点(1544.694,280),左边数据有误差,根据曲线走势,取最右边的一点(1544.556,280),得其3dB带宽|1544.694-1544.556|=0.138nm。
二、光纤FBG温度传感器的标定将原始数据进行线性拟合,得b=0.010649,a=1540.2141544.520 26.01544.682 41.01544.837 56.01545.029 75.01545.204 90.41545.373 105.0标定后,我们又测了两组数据真实值108.6 95测量值108.2 93.20可以看出,拟合还是比较标准的,但还是存在一定的误差。
三、光纤FBG应变传感器的——光纤称重传感器1564.404 01564.696 5001564.885 10001565.077 15001565.270 20001565.467 25001565.667 3000将原始数据进行线性拟合,得b=0.0000985,a=1544.615标定后,我们又测了三组数据真实值1000 2000 2500测量值1003.4082022.676 2478.746可以看出,在误差允许的范围内,拟合还是比较标准的。
四、思考题1、影响光纤FBG温度传感器的测量精度的因素有哪些?答:有操作失误、温度没有稳定就读值、光纤有损坏、系统误差等。
2、如何提高光纤FBG中心波长的计算精度?答:在最高点附近多测几组数值、整体多测几次求平均、读数时根据曲线的对称性在最高点附近两边取纵坐标相同的值再求中点。
五、心得体会通过本次实验,我了解了基于光纤布拉格光栅的应变和温度传感器的工作原理和特性,同时对传感器也有了更多的了解,测量是否精确也在一定程度上取决于标定的情况。


光纤光栅的应力和温度传感特性研究 (1)一光纤光栅传感器理论基础 (1)1 光纤光栅应力测量 (1)2 光纤光栅温度测量 (2)3 光纤光栅压力测量 (3)二光纤光栅传感器增敏与封装 (4)1 光纤光栅的应力增敏 (4)2 光纤光栅的温度增敏 (5)3 光纤光栅的温度减敏 (5)4 嵌入式敏化与封装 (6)5 粘敷式敏化与封装 (7)三光纤光栅传感器交叉敏感问题及其解决方法 (9)1 参考光纤光栅法 (10)2 双光栅矩阵运算法 (10)3 FBG与LPFG混合法 (11)4 不同包层直径熔接法 (12)5 啁啾光栅法 (12)光纤光栅的应力和温度传感特性研究一光纤光栅传感器理论基础1 光纤光栅应力测量由耦合模理论可知,光纤布拉格光栅(FBG)的中心反射波长为:2B eff n λ=Λ (1)式中:eff n 为导模的有效折射率,Λ为光栅的固有周期。
当波长满足布拉格条件式(1)时,入射光将被光纤光栅反射回去。
由公式(1)可知,光纤光栅的中心反射波长B λ随eff n 和Λ的改变而改变。
FBG 对于应力和温度都是很敏感的,应力通过弹光效应和光纤光栅周期Λ的变化来影响B λ,温度则是通过热光效应和热胀效应来影响B λ。
当光纤光栅仅受应力作用时,光纤光栅的折射率和周期发生变化,引起中心反射波长B λ移动,因此有:effBBeffn n λλ∆∆∆Λ=+Λ (2) 式中:eff n ∆为折射率的变化,∆Λ为光栅周期的变化。
光栅产生应力时的折射率变化:()21211112eff eff e effn n P P P n μμεε∆=---=-⎡⎤⎣⎦ (3) 式中:()21211112e eff P n P P μμ=--⎡⎤⎣⎦ (4) ε是轴向应力,μ是纤芯材料的泊松比,11P 、12P 是弹光系数,e P 是有效弹光系数。
假设光纤光栅是绝对均匀的,也就是说,光栅的周期相对变化率和光栅段的物理长度的相对变化率是一致的。
光纤光栅传感实验一、实验目的1. 理解光纤光栅的制作原理;2. 掌握光纤光栅传感的原理;3. 学会使用光纤光栅传感仪软件;4. 使用光纤光栅传感仪测量温度变化对输出波长的影响;5. 使用光纤光栅传感仪测量应力变化对输出波长的影响;二、实验原理光纤光栅传感的基本原理和光纤光栅传感测量的基本原理光纤光栅受温度T 和应变ε同时影响时,光纤光栅峰值波长会发生变化,其相对变化量可以写成:Δλ/λ=(α+ξ)ΔT+(1-Pe )ε (6)其中α、ξ分别是光纤的热膨胀系数和热光系数,其值α=0.55×10-6,ξ=8.3×10-6,即温度灵敏度大约是0.0136 nm /℃,(λ为1550nm );Pe 是有效光弹系数,大约为0.22,即应变灵敏度为0.001209 nm /με。
2.1光纤光栅温度传感器为了提高光纤光栅温度灵敏度,在光纤光栅温度传感器中,是将光纤光栅封装在温度增敏材料基座上,外部有不锈钢管保护,外面有加热装置。
如图4。
波长变化量及温度灵敏度分别为(请自行推算):Δλ/ΔT =((α+ξ) +(1-P )(αj -α))λ (7)[Δλ/ΔT =αt ]αt 定义为该温度传感器的温度灵敏度,可由实验获得,大约是αt =0.035nm/℃。
由测量到的波长的变化量可计算出温度的变化t-t 0:2.2光纤光栅应变传感器本实验仪的光纤光栅应变传感器是一种悬臂梁应变调谐机构。
应用材料力学原理可以严格计算出光纤光栅的应变,用于模拟环境物理量使光纤光栅产生的应变。
由光纤光栅的应变又可计算出传感光栅的波长变化。
图1光纤光栅示意图出 射 光布喇格光纤光栅 纤芯入射光 反射光光纤包层光纤光栅应变传感器原理图如图5光纤光栅粘接在悬臂梁距固定端根部x 位置,螺旋测微器调节挠度,由材料力学可知,光纤光栅的应变为:3)(3l dhx l -=ε (8) 其中l 、h 、d 分别表示梁的长度、挠度和中性面至表面的距离,η=1-PePe 是光纤有效光弹系数。
光纤光栅的应力和温度传感特性研究 (1)一光纤光栅传感器理论基础 (1)1 光纤光栅应力测量 (1)2 光纤光栅温度测量 (2)3 光纤光栅压力测量 (3)二光纤光栅传感器增敏与封装 (4)1 光纤光栅的应力增敏 (4)2 光纤光栅的温度增敏 (5)3 光纤光栅的温度减敏 (5)4 嵌入式敏化与封装 (6)5 粘敷式敏化与封装 (7)三光纤光栅传感器交叉敏感问题及其解决方法 (9)1 参考光纤光栅法 (10)2 双光栅矩阵运算法 (10)3 FBG与LPFG混合法 (11)4 不同包层直径熔接法 (12)5 啁啾光栅法 (12)光纤光栅的应力和温度传感特性研究一光纤光栅传感器理论基础1 光纤光栅应力测量由耦合模理论可知,光纤布拉格光栅(FBG)的中心反射波长为:2B eff n λ=Λ (1)式中:eff n 为导模的有效折射率,Λ为光栅的固有周期。
当波长满足布拉格条件式(1)时,入射光将被光纤光栅反射回去。
由公式(1)可知,光纤光栅的中心反射波长B λ随eff n 和Λ的改变而改变。
FBG 对于应力和温度都是很敏感的,应力通过弹光效应和光纤光栅周期Λ的变化来影响B λ,温度则是通过热光效应和热胀效应来影响B λ。
当光纤光栅仅受应力作用时,光纤光栅的折射率和周期发生变化,引起中心反射波长B λ移动,因此有:eff BB effn n λλ∆∆∆Λ=+Λ (2) 式中:eff n ∆为折射率的变化,∆Λ为光栅周期的变化。
光栅产生应力时的折射率变化:()21211112effeff e effn n P P P n μμεε∆=---=-⎡⎤⎣⎦ (3) 式中: ()21211112e eff P n P P μμ=--⎡⎤⎣⎦ (4) ε是轴向应力,μ是纤芯材料的泊松比,11P 、12P 是弹光系数,e P 是有效弹光系数。
假设光纤光栅是绝对均匀的,也就是说,光栅的周期相对变化率和光栅段的物理长度的相对变化率是一致的。