基本FIS编辑器(MATLAB模糊逻辑工具箱函数)
- 格式:docx
- 大小:41.24 KB
- 文档页数:13
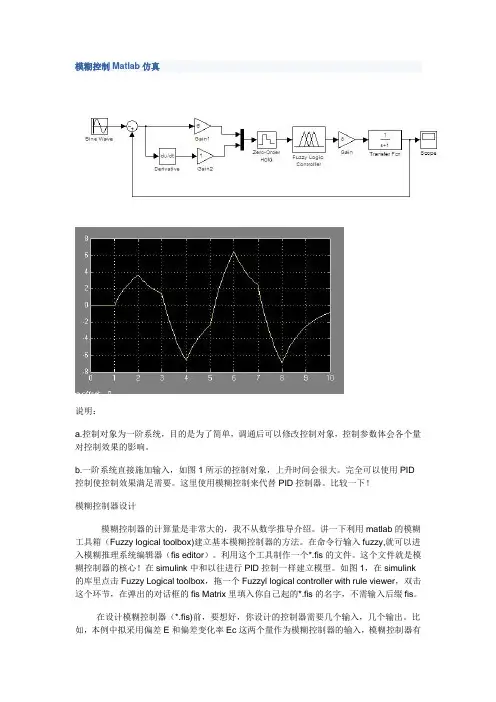
模糊控制Matlab仿真说明:a.控制对象为一阶系统,目的是为了简单,调通后可以修改控制对象,控制参数体会各个量对控制效果的影响。
b.一阶系统直接施加输入,如图1所示的控制对象,上升时间会很大。
完全可以使用PID 控制使控制效果满足需要。
这里使用模糊控制来代替PID控制器。
比较一下!模糊控制器设计模糊控制器的计算量是非常大的,我不从数学推导介绍。
讲一下利用matlab的模糊工具箱(Fuzzy logical toolbox)建立基本模糊控制器的方法。
在命令行输入fuzzy,就可以进入模糊推理系统编辑器(fis editor)。
利用这个工具制作一个*.fis的文件。
这个文件就是模糊控制器的核心!在simulink中和以往进行PID控制一样建立模型。
如图1,在simulink 的库里点击Fuzzy Logical toolbox,拖一个Fuzzyl logical controller with rule viewer,双击这个环节,在弹出的对话框的fis Matrix里填入你自己起的*.fis的名字,不需输入后缀fis。
在设计模糊控制器(*.fis)前,要想好,你设计的控制器需要几个输入,几个输出。
比如,本例中拟采用偏差E和偏差变化率Ec这两个量作为模糊控制器的输入,模糊控制器有一个输出。
很明显,这是利用模糊控制器代替PD控制的。
对应的模糊控制器的设计也要具有两个输入一个输出。
利用matlab的Fuzzy logical toolbox 设计模糊控制器(生成*.fis文件)的关键步骤:a.添加输入输出。
图3.fis编辑器默认的具有一个输出,添加第二个输入,并且分别命名为E,Ec,U。
b.确定隶属函数。
双击黄色和绿色的方框就可以进入隶属函数编辑对话框了。
设置E,Ec 的range为[-6,6],u的range为[-1,1]。
然后每一个变量再添加4个输入隶属函数,总共7个。
matlab提供了11种隶属函数,第一次用选择常用的三角形trimf,区别不大的。

通过算例熟悉MATLAB模糊控制工具箱设计一个二维模糊控制器控制一个一阶被控对象1()1G sTs=+,然后改变控制对象参数的大小,观察模糊控制的鲁棒性。
1、模糊推理的五个步骤1)输入变量的模糊化这是模糊推理的第一步,是获取输入变量,并确定它们的隶属函数,从而确定属于每个模糊集合的隶属度。
2) 应用模糊算子完成了输入模糊化,就知道了对于每个模糊规则,前提中每一个部分被满足的程度。
如果一个给定规则的前提有多个部分,则要应用模糊算子来获得一个数值,这个数值表示前提对于该规则的满足程度。
3) 应用推理方法推理的类型有mamdani和sugeno 推理。
Mamdani推理法是一种在模糊控制中普遍使用的方法,它本质上仍然是一种合成推理方法,只不过对模糊蕴涵关系取不同的形式而已。
Mamdani型推理,从每个规则的结果中得到的模糊集通过聚类运算后得到结果模糊集,被反模糊化后得到系统输出。
Sugeon型推理:其中每个规则的结果是输入的线性组合,而输出是结果的加权线性组合。
4) 输出的聚类由于决策是在对模糊推理系统中所有规则进行综合考虑的基础上做出的,因此必须以某种方式将规则结合起来以做出决策。
聚类就是这样一个过程,它将表示每个规则输出的模糊集结合成一个单独的模糊集。
聚类方法有max,probor(概率乘),sum。
其中,sum执行的是各规则输出集的简单相加。
5) 解模糊化解模糊化过程也叫反模糊化过程,它的输入是一个模糊集,既上一步的聚类输出模糊集,其输出为一个单值。
模糊集的聚类中包含很多输出值,因此必须进行反模糊化,以从集合中解析出一个单输出值。
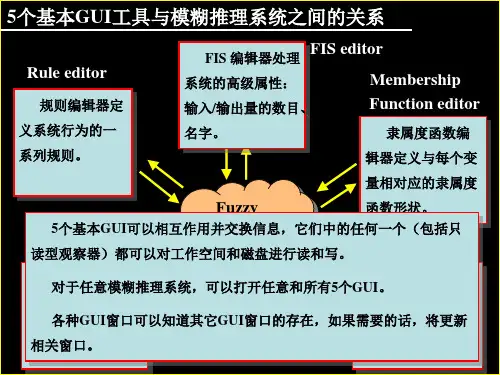
2、模糊逻辑工具箱的介绍模糊逻辑工具箱提供的图形用户界面(GUI)工具有五个:模糊推理系统(FIS)编辑器;隶属函数编辑器;模糊规则编辑器;模糊规则观察器;输出曲面观察器。
1)FIS编辑器:Matlab的FIS界面如图1所示。
FIS处理系统有多少个输入变量,输出变量,名称是什么,模糊算子“与”(min,prod乘积,custom自定义),“或”(max大,probor 概率统计方法,custom),推理方法(min,prod,custom),聚类方法(max,probor,sum,custom),解模糊的方法(centroid质心法,bisector中位线法,middle of maximum,largest of maximum,smallest of maximum)。

4 MATLAB模糊工具箱介绍Fuzzy Logic工具箱功能非常强大,利用它人们可以方便地建立模糊逻辑推理系统,并对其进行测试。
这里我们主要介绍它提供的5个图形化的系统设计工具。
4.1模糊推理系统编辑器启动模糊推理系统编辑器(FISE, Fuzzy Inference System Editer)的方法有两种,在MATLAB的命令窗口中输入“fuzzy”命令或者依次点击MATLAB软件左下角的“Start”,“Toolboxes”,“Fuzzy Logic”也可打开FISE,然后双击FIS Editor Viewer项。
FISE的图形界面如下图14示。
图1FISE图形界面4.2隶属函数编辑器在MATLAB的命令界面输入“mfedit”命令或者在模糊推理系统编辑器的“File” “Edit/Membership Functions”或者双击图14中红色矩形,都可打开隶属函数编辑器。
通过该编辑器可以设定和变更输入/输出语言变量的各自的语言值的隶属函数的类型及参数。
如下图15所示。
图2隶属函数编辑器界面4.3模糊规则编辑器在MATLAB的命令界面中输入“ruleedit”命令或者利用模糊推理系统编辑器的“File” “Edit/Rules”或双击图2里红色框旁的黑色的矩形框,都可以打开模糊规则编辑器。
通过该编辑器可以添加、修改和删除必要的模糊规则,其空白界面如下图3所示。
图3模糊规则编辑器界面4.4模糊规则观察器在MATLAB的命令界面输入“ruleview”命令,或者在前面介绍的三种编辑器中的任一个中选择相应的“View/Rules”,均可打开模糊规则观察器。
在模糊规则观察器中,以图形形式描述了模糊推理系统的推理过程,如下图4所示。
图4模糊规则浏览器界面4.5模糊推理输入输出变量特性观察器在MATLAB的命令窗口中输入“surfview”命令,或者在各个编辑器窗口选择相应菜单“View/Surface”,都可打开模糊推理输入输出曲面浏览器。


方法二:用MATLAB的模糊逻辑工具箱(Fuzzy toolbox)实现(陈老师整理)一、模糊逻辑推理系统的总体特征模糊控制由于不依赖对象的数学模型而受到广泛的重视,计算机仿真是研究模糊控制系统的重要手段之一。
由Math Works公司推出的Matlab软件,为控制系统的计算机仿真提供了强有力的工具,特别是在Matlab4.2以后的版本中推出的模糊工具箱(Fuzzy Toolbox),为仿真模糊控制系统提供了很大的方便。
由于这样的模块都是由相关领域的著名学者开发的,所以其可信度都是很高的,仿真结果是可靠的。
在Simulink环境下对PID控制系统进行建模是非常方便的,而模糊控制系统与PID控制系统的结构基本相同,仅仅是控制器不同。
所以,对模糊控制系统的建模关键是对模糊控制器的建模。
Matlab软件提供了一个模糊推理系统(FIS)编辑器,只要在Matlab命令窗口键入Fuzzy就可进入模糊控制器编辑环境。
二、Matlab模糊逻辑工具箱仿真1.模糊推理系统编辑器(Fuzzy)模糊推理系统编辑器用于设计和显示模糊推理系统的一些基本信息,如推理系统的名称,输入、输出变量的个数与名称,模糊推理系统的类型、解模糊方法等。
其中模糊推理系统可以采用Mandani或Sugeuo两种类型,解模糊方法有最大隶属度法、重心法、加权平均等。
打开模糊推理系统编辑器,在MATLAB的命令窗(command window)内键入:fuzzy 命令,弹出模糊推理系统编辑器界面,如下图所示。
因为我们用的是两个输入,所以在Edit菜单中,选Add variable… ->input,加入新的输入input,如下图所示。
选择input(选中为红框),在界面右边文字输入处键入相应的输入名称,例如,温度输入用tmp-input, 磁能输入用 mag-input,等。
2.隶属度函数编辑器(Mfedit)该编辑器提供一个友好的人机图形交互环境,用来设计和修改模糊推理系中各语言变量对应的隶属度函数的相关参数,如隶属度函数的形状、范围、论域大小等,系统提供的隶属度函数有三角、梯形、高斯形、钟形等,也可用户自行定义。
num=20;den=[8 6 1];[a1,b1,c1,d]=tf2ss(num,den); T=0.01;h=T;N=500;R=1.5*ones(1,N);%pide=0;de=0;ie=0;kp=4;ki=0.5;kd=1.5;x=[0;0];for k=1:Nu1=-(kp*e+ki*ie+kd*de);k0=a1*x+b1*u1;k1=a1*(x+h*k0/2)+b1*u1;k2=a1*(x+h*k1/2)+b1*u1;k3=a1*(x+h*k2)+b1*u1;x=x+(k0+2*k1+2*k2+k3)*h/6; y=c1*x+d*u1;e1=e;e=y-R(1,k);de=(e-e1)/T;ie=e*T+ie;yy2(1,k)=y;enda=newfis('simple1');a=addvar(a,'input','e',[-5 5]);a=addmf(a,'input',1,'NB','trapmf',[-5,-5,-5,-4]);a=addmf(a,'input',1,'NM','trapmf',[-5,-4,-3,-2]);a=addmf(a,'input',1,'NS','trapmf',[-3,-2,-1,0]);a=addmf(a,'input',1,'ZE','trimf',[-1,0,1]);a=addmf(a,'input',1,'PS','trapmf',[0,1,2,3]);a=addmf(a,'input',1,'PM','trapmf',[2,3,4,5]);a=addmf(a,'input',1,'PB','trapmf',[4,5,5,5]);a=addvar(a,'input','de',[-5 5]);a=addmf(a,'input',2,'NB','trapmf',[-5,-5,-5,-4]);a=addmf(a,'input',2,'NM','trapmf',[-5,-4,-3,-2]);a=addmf(a,'input',2,'NS','trapmf',[-3,-2,-1,0]);a=addmf(a,'input',2,'ZE','trimf',[-1,0,1]);a=addmf(a,'input',2,'PS','trapmf',[0,1,2,3]);a=addmf(a,'input',2,'PM','trapmf',[2,3,4,5]);a=addmf(a,'input',2,'PB','trapmf',[4,5,5,5]);a=addvar(a,'output','kp',[-5 5]);a=addmf(a,'output',1,'NB','trapmf',[-5,-5,-5,-4]);a=addmf(a,'output',1,'NM','trapmf',[-5,-4,-3,-2]);a=addmf(a,'output',1,'NS','trapmf',[-3,-2,-1,0]);a=addmf(a,'output',1,'ZE','trimf',[-1,0,1]);a=addmf(a,'output',1,'PS','trapmf',[0,1,2,3]);a=addmf(a,'output',1,'PM','trapmf',[2,3,4,5]);a=addmf(a,'output',1,'PB','trapmf',[4,5,5,5]);rulelist1=[1 1 7 1 1;1 2 7 1 1;1 3 6 1 1;1 4 6 1 1;1 5 5 1 1;1 6 4 1 1;1 7 4 1 1;2 1 7 1 1;2 2 7 1 1;23 6 1 1;245 1 1;2 5 5 1 1;26 4 1 1;2 73 1 1;3 1 6 1 1;3 2 6 1 1;3 3 6 1 1;345 1 1;3 5 4 1 1;36 3 1 1;3 7 3 1 1;4 1 6 1 1;4 2 6 1 1;4 35 1 1;4 4 4 1 1;4 5 3 1 1;46 2 1 1;4 7 2 1 1;5 1 5 1 1;5 2 5 1 1;5 3 4 1 1;5 4 3 1 1;5 5 3 1 1;56 2 1 1;5 7 2 1 1;6 1 5 1 1;6 2 4 1 1;6 3 3 1 1;6 4 2 1 1;6 5 2 1 1;6 6 2 1 1;6 7 1 1 1;7 1 4 1 1;7 2 4 1 1;7 3 2 1 1;7 4 2 1 1;7 5 2 1 1;7 6 1 1 1;7 7 1 1 1]; a=addrule(a,rulelist1);b=newfis('simple2');b=addvar(b,'input','e',[-5 5]);b=addmf(b,'input',1,'NB','trapmf',[-5,-5,-5,-4]);b=addmf(b,'input',1,'NM','trapmf',[-5,-4,-3,-2]);b=addmf(b,'input',1,'NS','trapmf',[-3,-2,-1,0]);b=addmf(b,'input',1,'ZE','trimf',[-1,0,1]);b=addmf(b,'input',1,'PS','trapmf',[0,1,2,3]);b=addmf(b,'input',1,'PM','trapmf',[2,3,4,5]);b=addmf(b,'input',1,'PB','trapmf',[4,5,5,5]);b=addvar(b,'input','de',[-5 5]);b=addmf(b,'input',2,'NB','trapmf',[-5,-5,-5,-4]);b=addmf(b,'input',2,'NM','trapmf',[-5,-4,-3,-2]);b=addmf(b,'input',2,'NS','trapmf',[-3,-2,-1,0]);b=addmf(b,'input',2,'ZE','trimf',[-1,0,1]);b=addmf(b,'input',2,'PS','trapmf',[0,1,2,3]);b=addmf(b,'input',2,'PM','trapmf',[2,3,4,5]);b=addmf(b,'input',2,'PB','trapmf',[4,5,5,5]);b=addvar(b,'output','ki',[-5 5]);b=addmf(b,'output',1,'NB','trapmf',[-5,-5,-5,-4]);b=addmf(b,'output',1,'NM','trapmf',[-5,-4,-3,-2]);b=addmf(b,'output',1,'NS','trapmf',[-3,-2,-1,0]);b=addmf(b,'output',1,'ZE','trimf',[-1,0,1]);b=addmf(b,'output',1,'PS','trapmf',[0,1,2,3]);b=addmf(b,'output',1,'PM','trapmf',[2,3,4,5]);b=addmf(b,'output',1,'PB','trapmf',[4,5,5,5]);rulelist2=[1 1 1 1 1;1 2 1 1 1;1 3 2 1 1;1 4 2 1 1;1 5 3 1 1;1 6 4 1 1;1 7 4 1 1;2 1 1 1 1;2 2 1 1 1;23 2 1 1;24 3 1 1;25 3 1 1;26 4 1 1;2 7 4 1 1;3 1 1 1 1;3 2 2 1 1;3 3 3 1 1;34 3 1 1;35 4 1 1;36 5 1 1;3 7 5 1 1;4 1 2 1 1;4 2 2 1 1;4 3 3 1 1;4 4 4 1 1;45 5 1 1;46 6 1 1;4 7 6 1 1;5 1 2 1 1;5 2 3 1 1;5 3 4 1 1;5 4 5 1 1;5 5 5 1 1;56 6 1 1;5 7 7 1 1;6 1 4 1 1;6 2 4 1 1;6 3 5 1 1;6 4 5 1 1;6 5 6 1 1;6 67 1 1;6 7 7 1 1;7 1 4 1 1;7 2 4 1 1;7 3 5 1 1;7 4 6 1 1;7 5 6 1 1;7 6 7 1 1;7 7 7 1 1]; b=addrule(b,rulelist2);c=newfis('simple3');c=addvar(c,'input','e',[-5 5]);c=addmf(c,'input',1,'NB','trapmf',[-5,-5,-5,-4]);c=addmf(c,'input',1,'NM','trapmf',[-5,-4,-3,-2]);c=addmf(c,'input',1,'NS','trapmf',[-3,-2,-1,0]);c=addmf(c,'input',1,'ZE','trimf',[-1,0,1]);c=addmf(c,'input',1,'PS','trapmf',[0,1,2,3]);c=addmf(c,'input',1,'PM','trapmf',[2,3,4,5]);c=addmf(c,'input',1,'PB','trapmf',[4,5,5,5]);c=addvar(c,'input','de',[-5 5]);c=addmf(c,'input',2,'NB','trapmf',[-5,-5,-5,-4]);c=addmf(c,'input',2,'NM','trapmf',[-5,-4,-3,-2]);c=addmf(c,'input',2,'NS','trapmf',[-3,-2,-1,0]);c=addmf(c,'input',2,'ZE','trimf',[-1,0,1]);c=addmf(c,'input',2,'PS','trapmf',[0,1,2,3]);c=addmf(c,'input',2,'PM','trapmf',[2,3,4,5]);c=addmf(c,'input',2,'PB','trapmf',[4,5,5,5]);c=addvar(c,'output','kd',[-5 5]);c=addmf(c,'output',1,'NB','trapmf',[-5,-5,-5,-4]);c=addmf(c,'output',1,'NM','trapmf',[-5,-4,-3,-2]);c=addmf(c,'output',1,'NS','trapmf',[-3,-2,-1,0]);c=addmf(c,'output',1,'ZE','trimf',[-1,0,1]);c=addmf(c,'output',1,'PS','trapmf',[0,1,2,3]);c=addmf(c,'output',1,'PM','trapmf',[2,3,4,5]);c=addmf(c,'output',1,'PB','trapmf',[4,5,5,5]);rulelist3=[1 1 1 1 1;1 2 1 1 1;1 3 1 1 1;1 4 1 1 1;1 5 1 1 1;1 6 1 1 1;1 7 1 1 1;2 1 2 1 1;2 2 2 1 1;23 2 1 1;24 2 1 1;25 2 1 1;26 2 1 1;2 7 2 1 1;3 1 3 1 1;3 2 3 1 1;3 3 3 1 1;34 3 1 1;35 3 1 1;36 3 1 1;3 7 3 1 1;4 1 4 1 1;4 2 3 1 1;4 3 3 1 1;4 4 3 1 1;45 3 1 1;46 3 1 1;4 7 4 1 1;5 1 4 1 1;5 2 4 1 1;5 3 4 1 1;5 4 4 1 1;5 5 4 1 1;56 4 1 1;5 7 4 1 1;6 1 5 1 1;6 2 5 1 1;6 3 5 1 1;6 4 5 1 1;6 5 5 1 1;6 6 5 1 1;6 7 4 1 1;7 1 6 1 1;7 2 6 1 1;7 3 6 1 1;7 4 6 1 1;7 5 6 1 1;7 6 6 1 1;7 7 6 1 1]; c=addrule(c,rulelist3);figure(2);gensurf(c)e=0;de=0;ie=0;x=[0;0];ke=30;kd=20;kup=5;kui=0.3;kud=0.7;for k=1:Ne1=ke*e;de1=kd*de;if e1>=5e1=5;elseif e1<=-5e1=-5;endif de1>=5de1=5;elseif de1<=-5de1=-5;endin=[e1 de1];u1=evalfis(in,a);u2=evalfis(in,b);u3=evalfis(in,c);kp=u1/10+kup;ki=u2/10+kui;kd=u3/10+kud;u=-(kp*e+ki*ie+kd*de);k0=a1*x+b1*u;k1=a1*(x+h*k0/2)+b1*u;k2=a1*(x+h*k1/2)+b1*u;k3=a1*(x+h*k2)+b1*u;x=x+(k0+2*k1+2*k2+k3)*h/6; y=c1*x+d*u;yy(1,k)=y;e1=e;e=y-R(1,k);de=(e-e1)/T;ie=ie+T*e;endkk=[1:N]*T;figure(1);plot(kk,R,'k',kk,yy(1,:),'r',kk,yy2(1,:),'g'); gtext('FSA-PID');gtext('PID');num=20;den=[1.6,4.4,1];[a1,b,c,d]=tf2ss(num,den);x=[0;0];T=0.01;h=T;N=1000;%PID CONTROLe=0;de=0;ie=0;kp=5;ki=1.3;kd=0.1;for k=1:Nuu(1,k)=-(kp*e+ki*de+kd*ie); u=uu(1,k);k0=a1*x+b*u;k1=a1*(x+h*k0/2)+b*u;k2=a1*(x+h*k1/2)+b*u;k3=a1*(x+h*k2)+b*u;x=x+(k0+2*k1+2*k2+k3)*h/6;y=c*x+d*u;t(1,k)=k*T;if k<=300R(1,k)=t(1,k)/3;elseif k<=700R(1,k)=1.0;elseif k<=1000R(1,k)=(10-t(1,k))/3;ende1=e;e=y-R(1,k);de=(e-e1)/T;ie=e*T+ie;yy1(1,k)=y;enda=newfis('simple');a=addvar(a,'input','e',[-6 6]);a=addmf(a,'input',1,'NB','trapmf',[-6,-6,-5,-3]); a=addmf(a,'input',1,'NS','trapmf',[-5,-3,-2,0]);a=addmf(a,'input',1,'ZR','trimf',[-2,0,2]);a=addmf(a,'input',1,'PS','trapmf',[0,2,3,5]);a=addmf(a,'input',1,'PB','trapmf',[3,5,6,6]);a=addvar(a,'input','de',[-6 6]);a=addmf(a,'input',2,'NB','trapmf',[-6,-6,-5,-3]); a=addmf(a,'input',2,'NS','trapmf',[-5,-3,-2,0]);a=addmf(a,'input',2,'ZR','trimf',[-2,0,2]);a=addmf(a,'input',2,'PS','trapmf',[0,2,3,5]);a=addmf(a,'input',2,'PB','trapmf',[3,5,6,6]);a=addvar(a,'output','u',[-3 3]);a=addmf(a,'output',1,'NB','trapmf',[-3,-3,-2,-1]); a=addmf(a,'output',1,'NS','trimf',[-2,-1,0]);a=addmf(a,'output',1,'ZR','trimf',[-1,0,1]);a=addmf(a,'output',1,'PS','trimf',[0,1,2]);a=addmf(a,'output',1,'PB','trapmf',[1,2,3,3]);rr=[5 5 4 4 3;5 4 4 3 3;4 4 3 3 2;4 3 3 2 2;3 3 2 2 1]; r1=zeros(prod(size(rr)),3);k=1;for i=1:size(rr,1)for j=1:size(rr,2)r1(k,:)=[i,j,rr(i,j)];k=k+1;endend[r,s]=size(r1);r2=ones(r,2);rulelist=[r1,r2];a=addrule(a,rulelist);e=0;de=0;ke=40;kd=1.5;ku=1;for k=1:Ne1=ke*e;de1=kd*de;if e1>=6e1=6;elseif e1<=-6e1=-6;endif de1>=6de1=6;elseif de1<=-6de1=-6;endin=[e1 de1];uu(1,k)=ku*evalfis(in,a); u=uu(1,k);k0=a1*x+b*u;k1=a1*(x+h*k0/2)+b*u;k2=a1*(x+h*k1/2)+b*u;k3=a1*(x+h*k2)+b*u;x=x+(k0+2*k1+2*k2+k3)*h/6; y=c*x+d*u;t(1,k)=k*T;if k<=300R(1,k)=t(1,k)/3;elseif k<=700R(1,k)=1.0;elseif k<=1000R(1,k)=(10-t(1,k))/3;ende1=e;e=y-R(1,k);de=(e-e1)/T;yy(1,k)=y;endkk=[1:N]*T;figure(1);plot(kk,R,'k',kk,yy,'k',kk,yy1,'r'); gtext('FUZZY');gtext('n');gtext('PID');。

基本FIS编辑器函数fuzzy格式 fuzzy %弹出未定义的基本FIS编辑器fuzzy(fismat) %使用fuzzy('tipper'),弹出下图FIS编辑器。
编辑器是任意模糊推理系统的高层显示,它允许你调用各种其它的编辑器来对其操作。
此界面允许你方便地访问所有其它的编辑器,并以最灵活的方式与模糊系统进行交互。
方框图:窗口上方的方框图显示了输入、输出和它们中间的模糊规则处理器。
单击任意一个变量框,使选中的方框成为当前变量,此时它变成红色高亮方框。
双击任意一个变量,弹出隶属度函数编辑器,双击模糊规则编辑器,弹出规则编辑器。
菜单项:FIS编辑器的菜单棒允许你打开相应的工具,打开并保存系统。
·File菜单包括:New mamdani FIS … 打开新mamdani型系统;New Sugeno FIS …打开新Sugeno型系统;Open from disk …从磁盘上打开指定的.fis文件系统;Save to disk 保存当前系统到磁盘上的一个.fis文件上;Save to disk as … 重命名方式保存当前系统到磁盘上;Open from workspace … 从工作空间中指定的FIS结构变量装入一个系统;Save to workspace …保存系统到工作空间中当前命名的FIS结构变量中;Save to workspace as …保存系统到工作空间中指定的FIS结构变量中;Close windows 关闭GUI;·Edit菜单包括:Add input 增加另一个输入到当前系统中;Add output 增加另一个输出到当前系统中;Remove variable 删除一个所选的变量;Undo 恢复当前最近的改变;Edit MFs …调用隶属度函数编辑器;Edit rules …调用规则编辑器;Edit anfis …只对单输出Sugeno型系统调用编辑器;View rules …调用规则观察器;View surface … 调用曲面观察器。

defuzz matlab代码以下是一个简单的模糊逻辑解模糊的 MATLAB 代码示例: matlab.% 创建模糊逻辑系统。
fis = newfis('fis');% 添加输入变量。
fis = addvar(fis, 'input', 'Input1', [0 10]);fis = addvar(fis, 'input', 'Input2', [0 10]);% 添加输出变量。
fis = addvar(fis, 'output', 'Output1', [0 10]); % 添加隶属函数。
fis = addmf(fis, 'input', 1, 'Low', 'trimf', [0 0 5]);fis = addmf(fis, 'input', 1, 'High', 'trimf', [0 5 10]); fis = addmf(fis, 'input', 2, 'Low', 'trimf', [0 0 5]);fis = addmf(fis, 'input', 2, 'High', 'trimf', [0 5 10]); fis = addmf(fis, 'output', 1, 'Low', 'trimf', [0 0 5]);fis = addmf(fis, 'output', 1, 'High', 'trimf', [0 5 10]);% 添加模糊规则。
ruleList = [1 1 1 1 1;2 2 1 1 1;1 2 2 1 1];fis = addrule(fis, ruleList);% 模糊化输入。

基本FIS编辑器函数fuzzy格式 fuzzy %弹出未定义的基本FIS编辑器fuzzy(fismat) %使用fuzzy('tipper'),弹出下图FIS编辑器。
编辑器是任意模糊推理系统的高层显示,它允许你调用各种其它的编辑器来对其操作。
此界面允许你方便地访问所有其它的编辑器,并以最灵活的方式与模糊系统进行交互。
方框图:窗口上方的方框图显示了输入、输出和它们中间的模糊规则处理器。
单击任意一个变量框,使选中的方框成为当前变量,此时它变成红色高亮方框。
双击任意一个变量,弹出隶属度函数编辑器,双击模糊规则编辑器,弹出规则编辑器。
图6-19菜单项:FIS编辑器的菜单棒允许你打开相应的工具,打开并保存系统。
·File菜单包括:New mamdani FIS … 打开新mamdani型系统;New Sugeno FIS …打开新Sugeno型系统;Open from disk …从磁盘上打开指定的.fis文件系统;Save to disk 保存当前系统到磁盘上的一个.fis文件上;Save to disk as … 重命名方式保存当前系统到磁盘上;Open from workspace … 从工作空间中指定的FIS结构变量装入一个系统;Save to workspace …保存系统到工作空间中当前命名的FIS结构变量中;Save to workspace as …保存系统到工作空间中指定的FIS结构变量中;Close windows 关闭GUI;·Edit菜单包括:Add input 增加另一个输入到当前系统中;Add output 增加另一个输出到当前系统中;Remove variable 删除一个所选的变量;Undo 恢复当前最近的改变;·View 菜单包括:Edit MFs …调用隶属度函数编辑器;Edit rules …调用规则编辑器;Edit anfis …只对单输出Sugeno型系统调用编辑器;View rules …调用规则观察器;View surface … 调用曲面观察器。

MATLAB模糊逻辑工具箱函数说明:本文档中所列出的函数适用于MA TLAB5.3以上版本,为了简明起见,只列出了函数名,若需要进一步的说明,请参阅MATLAB的帮助文档。
1.GUI工具Anfisedit 打开ANFIS编辑器GUIFuzzy 调用基本FIS编辑器Mfedit 隶属度函数编辑器Ruleedit 规则编辑器和语法解析器Ruleview 规则观察器和模糊推理方框图Surfview 输出曲面观察器2.隶属度函数dsigmf 两个sigmoid型隶属度函数之差组成的隶属度函数gauss2mf 建立两边型高斯隶属度函数gaussmf 建立高斯曲线隶属度函数gbellmf 建立一般钟型隶属度函数pimf 建立Π型隶属度函数psigmf 通过两个sigmoid型隶属度函数的乘积构造隶属度函数smf 建立S-型隶属度函数sigmf 建立Sigmoid型隶属度函数trapmf 建立梯形隶属度函数trimf 建立三角形隶属度函数zmf 建立Z-型隶属度函数3.FIS数据结构管理addmf 向模糊推理系统(FIS)的语言变量添加隶属度函数addrule 向模糊推理系统(FIS)的语言变量添加规则addvar 向模糊推理系统(FIS)添加语言变量defuzz 对隶属度函数进行反模糊化evalfis 完成模糊推理计算evalmf 通过隶属度函数计算gensurf 生成一个FIS输出曲面getfis 得到模糊系统的属性mf2mf 在两个隶属度函数之间转换参数newfis 创建新的FISparsrule 解析模糊规则plotfis 绘制一个FISplotmf 绘制给定语言变量的所有隶属度函数的曲线readfis 从磁盘装入一个FISrmmf 从FIS中删除某一语言变量的某一隶属度函数rmvar 从FIS中删除某一语言变量setfis 设置模糊系统的属性showfis 以分行的形式显示FIS结构的所有属性showrule 显示FIS的规则writefis 保存FIS到磁盘上4.先进技术anfis Sugeno型模糊推理系统(FIS)的训练程序(只适用于MEX)fcm 模糊C均值聚类genfis1 不使用数据聚类方法从数据生成FIS结构genfis2 使用减法聚类方法从数据生成FIS结构subclust 用减法聚类方法寻找聚类中心5.Simulink仿真块fuzblock Simulink模糊逻辑控制器库sffis 用于Simulink的模糊推理S-函数6.演示defuzzdm 反模糊化方法fcmdemo FCM聚类显示(二维)fuzdemos 列出所有模糊逻辑工具箱的演示程序gasdemo 使用子聚类节省燃料的ANFIS演示juggler 带规则观察器的弹球游戏器invkine 单机械臂倒立摆运动irisfcm FCM聚类显示(四维)noisedm 自适应消除噪声slbb 球和棒控制(Simulink)slcp 倒立摆控制(Simulink)sltank 水位控制(Simulink)sltankrule 带规则观察器的水位控制(Simulink)sltbu 卡车入库(只有Simulink方式)。
方法二:用MATLAB 的模糊逻辑工具箱(Fuzzy toolbox)实现(陈老师整理)一、模糊逻辑推理系统的总体特征模糊控制由于不依赖对象的数学模型而受到广泛的重视,计算机仿真是研究模糊控制系统的重要手段之一。
由Math Works 公司推出的Matlab 软件,为控制系统的计算机仿真提供了强有力的工具,特别是在Matlab4.2 以后的版本中推出的模糊工具箱(Fuzzy Toolbox) ,为仿真模糊控制系统提供了很大的方便。
由于这样的模块都是由相关领域的著名学者开发的,所以其可信度都是很高的,仿真结果是可靠的。
在Simulink 环境下对PID 控制系统进行建模是非常方便的,而模糊控制系统与PID 控制系统的结构基本相同,仅仅是控制器不同。
所以,对模糊控制系统的建模关键是对模糊控制器的建模。
Matlab 软件提供了一个模糊推理系统( FIS)编辑器,只要在Matlab 命令窗口键入Fuzzy 就可进入模糊控制器编辑环境。
二、Matlab模糊逻辑工具箱仿真1. 模糊推理系统编辑器( Fuzzy )模糊推理系统编辑器用于设计和显示模糊推理系统的一些基本信息,如推理系统的名称,输入、输出变量的个数与名称,模糊推理系统的类型、解模糊方法等。
其中模糊推理系统可以采用Mandani或Sugeuo两种类型,解模糊方法有最大隶属度法、重心法、加权平均等。
打开模糊推理系统编辑器,在MATLAB的命令窗 ( commandw indow)内键入:fuzzy 命令,弹出模糊推理系统编辑器界面,如下图所示。
因为我们用的是两个输入,所以在Edit 菜单中,选Add variable ⋯->input, 加入新的输入input, 如下图所示。
选择input(选中为红框), 在界面右边文字输入处键入相应的输入名称,例如, 温度输入用tmp-input,磁能输入用mag-input ,等。
2. 隶属度函数编辑器(Mfedit)该编辑器提供一个友好的人机图形交互环境,用来设计和修改模糊推理系中各语言变量对应的隶属度函数的相关参数,如隶属度函数的形状、范围、论域大小等,系统提供的隶属度函数有三角、梯形、高斯形、钟形等,也可用户自行定义。
实验六模糊推理系统(FIS)的设计与仿真一、实验目的:1.认识MATLAB模糊逻辑工具箱的功能和特点;2.了解MATLAB模糊逻辑工具箱的五个图形化系统设计工具的功能;3.能够运用MATLAB模糊逻辑工具箱对模糊逻辑系统进行正确的参数设置;4.掌握基于Simulink的模糊逻辑系统模块的建立。
二、实验工具:MATLAB软件(6.1以上版本)。
三、实验内容及步骤:(一)PART A MATLAB模糊逻辑工具箱设计思想在MA TLAB中提供了Fuzzy Logic Toolbox(FIS,Fuzzy Inference System),主要有五个界面组成:(1)FIS Editor (模糊推理编译器)(2)Membership Function Editor (隶属度函数编辑器)(3)Rule Editor (模糊规则编辑器)(4)Rule Viewer (模糊规则浏览器)(5)Surface Viewer(模糊推理输入输出曲面视图)1. 模糊推理编译器(1)在MATLAB命令窗口中输入:fuzzy ,激活FIS Editor。
Fig. 1 MAMDANIFIS Editor用于建立模糊逻辑系统的整体框架,包括输入与输出数目、去模糊化方法等。
(2)MATLAB 提供两个逻辑推理MAMDANI 和SUGENO 方法。
Fig. 2 SUGENO窗口左下方的五种算法分别是:And Method :“与”算法;Or Method :“或”算法;Implication :蕴涵算法;Aggregation:综合;Deffuzification: 清晰化。
(3) 编辑FIS维数:在添加变量时可Edit——Add Variable ——Output2. 隶属度编辑器双击任意输入与输出模块,打开如下Membership Function Editor:Fig. 3 Membership Function EditorType:隶属度函数类型;Range:集合论域的取值;Params:曲线的拐点。
方法二:用MATLAB的模糊逻辑工具箱(Fuzzy toolbox)实现(陈老师整理)一、模糊逻辑推理系统的总体特征模糊控制由于不依赖对象的数学模型而受到广泛的重视,计算机仿真是研究模糊控制系统的重要手段之一。
由Math Works公司推出的Matlab软件,为控制系统的计算机仿真提供了强有力的工具,特别是在Matlab4.2以后的版本中推出的模糊工具箱(Fuzzy Toolbox),为仿真模糊控制系统提供了很大的方便。
由于这样的模块都是由相关领域的著名学者开发的,所以其可信度都是很高的,仿真结果是可靠的。
在Simulink环境下对PID控制系统进行建模是非常方便的,而模糊控制系统与PID控制系统的结构基本相同,仅仅是控制器不同。
所以,对模糊控制系统的建模关键是对模糊控制器的建模。
Matlab软件提供了一个模糊推理系统(FIS)编辑器,只要在Matlab命令窗口键入Fuzzy就可进入模糊控制器编辑环境。
二、Matlab模糊逻辑工具箱仿真1.模糊推理系统编辑器(Fuzzy)模糊推理系统编辑器用于设计和显示模糊推理系统的一些基本信息,如推理系统的名称,输入、输出变量的个数与名称,模糊推理系统的类型、解模糊方法等。
其中模糊推理系统可以采用Mandani或Sugeuo两种类型,解模糊方法有最大隶属度法、重心法、加权平均等。
打开模糊推理系统编辑器,在MATLAB的命令窗(command window)内键入:fuzzy 命令,弹出模糊推理系统编辑器界面,如下图所示。
因为我们用的是两个输入,所以在Edit菜单中,选Add variable… ->input,加入新的输入input,如下图所示。
选择input(选中为红框),在界面右边文字输入处键入相应的输入名称,例如,温度输入用tmp-input, 磁能输入用 mag-input,等。
2.隶属度函数编辑器(Mfedit)该编辑器提供一个友好的人机图形交互环境,用来设计和修改模糊推理系中各语言变量对应的隶属度函数的相关参数,如隶属度函数的形状、范围、论域大小等,系统提供的隶属度函数有三角、梯形、高斯形、钟形等,也可用户自行定义。
基本FIS编辑器函数fuzzy格式 fuzzy %弹出未定义的基本FIS编辑器fuzzy(fismat) %使用fuzzy('tipper'),弹出下图FIS编辑器。
编辑器是任意模糊推理系统的高层显示,它允许你调用各种其它的编辑器来对其操作。
此界面允许你方便地访问所有其它的编辑器,并以最灵活的方式与模糊系统进行交互。
方框图:窗口上方的方框图显示了输入、输出和它们中间的模糊规则处理器。
单击任意一个变量框,使选中的方框成为当前变量,此时它变成红色高亮方框。
双击任意一个变量,弹出隶属度函数编辑器,双击模糊规则编辑器,弹出规则编辑器。
图6-19菜单项:FIS编辑器的菜单棒允许你打开相应的工具,打开并保存系统。
·File菜单包括:New mamdani FIS … 打开新mamdani型系统;New Sugeno FIS …打开新Sugeno型系统;Open from disk …从磁盘上打开指定的.fis文件系统;Save to disk 保存当前系统到磁盘上的一个.fis文件上;Save to disk as … 重命名方式保存当前系统到磁盘上;Open from workspace … 从工作空间中指定的FIS结构变量装入一个系统;Save to workspace …保存系统到工作空间中当前命名的FIS结构变量中;Save to workspace as …保存系统到工作空间中指定的FIS结构变量中;Close windows 关闭GUI;·Edit菜单包括:Add input 增加另一个输入到当前系统中;Add output 增加另一个输出到当前系统中;Remove variable 删除一个所选的变量;Undo 恢复当前最近的改变;·View 菜单包括:Edit MFs …调用隶属度函数编辑器;Edit rules …调用规则编辑器;Edit anfis …只对单输出Sugeno型系统调用编辑器;View rules …调用规则观察器;View surface … 调用曲面观察器。
弹出式菜单:用五个弹出式菜单来改变模糊蕴含过程中五个基本步骤的功能:·And method:为一个定制操作选择min、prod或Custom;·Or method:为一个定制操作选择max、probor(概率)或Custom;·Implication method:为一个定制操作选择min、prod或Custom;此项对Sugeno型模糊系统不可用。
·Aggregation method:为一个定制操作选择max、sum、probor或Custom。
此项对Sugeno型模糊系统不可用。
·Defuzzification method:对Mamdani型推理,为一个定制操作选择centroid(面积中心法)、bisector(面积平分法)、mom(平均最大隶属度法)、som(最大隶属度最小值法)、lom(最大隶属度最大值法)或Custom。
对Sugeno 型推理,在wtaver(加权平均)或wtsum(加权和)之间选择。
6.1.15 隶属函数编辑器函数mfedit格式 mfedit('a')mfedit(a)mfedit说明 mfedit('a')生成一个隶属函数编辑器,他允许你检查和修改存储在文件a.fis中FIS结构的所有隶属函数。
如图,mfedit('tank')以这种方式打开隶属函数编辑器并装入tank.fis中存储的所有隶属函数。
mfedit(a)对于FIS结构操作一个MATLAB工作空间变量a。
Mfedit可单独弹出没有装入FIS的隶属函数编辑器图6-20菜单项:在ANFIS编辑器GUI上,有一个菜单棒允许你打开相关的GUI工具、打开和保存系统等。
File菜单与FIS编辑器上的File菜单功能相同。
·Edit菜单项包括:Add MF…为当前语言变量增加隶属度函数;Add custom MF…为当前语言变量增加定制的隶属度函数;Remove current MF 删除当前的隶属度函数;Remove all MFS 删除当前语言变量的所有隶属度函数;Undo 恢复当前最近的改变。
·View菜单项包括:Edit FIS properties…调用FIS编辑器;Edit rules…调用规则编辑器;View rules…调用规则观察器;View surface…调用曲面观察器。
6.2 模糊推理结构FIS6.2.1 不使用数据聚类方法从数据生成FIS结构函数genfis1格式 fismat = genfis1(data)fismat = genfis1(data,numMFs,inmftype, outmftype)说明 genfis1为anfis训练生成一个Sugeno型作为初始条件的FIS结构(初始隶属函数)。
genfis1(data,numMFs,inmftype, outmftype)使用对数据的网格分割方法,从训练数据集生成一个FIS结构。
Data是训练数据矩阵,除最后一列表示单一输出数据外,它的其它各列表示输入数据。
NumMFs是一个向量,它的坐标指定与每一输入相关的隶属函数的数量。
如果你想使用每个输入相关的相同数量的隶属函数,那么只须使numMFs成为一个数就足够了。
Inmftype是一个字符串数组,它的每行指定与每个输入相关的隶属函数类型。
outmftype是一个字符串数组,它的指定与每个输出相关的隶属函数类型例6-19>>data = [rand(10,1) 10*rand(10,1)-5 rand(10,1)];>>numMFs = [3 7];>>mfType = str2mat('pimf','trimf');>>fismat = genfis1(data,numMFs,mfType);>> [x,mf] = plotmf(fismat,'input',1);>>subplot(2,1,1), plot(x,mf);>>xlabel('input 1 (pimf)');>>[x,mf] = plotmf(fismat,'input',2);>>subplot(2,1,2), plot(x,mf);>>xlabel('input 2 (trimf)');结果为图6-21。
图6-216.2.2 使用减法聚类方法从数椐生成FIS结构函数genfis2格式 fismat = genfis2(Xin,Xout,radii)fismat = genfis2(Xin,Xout,radii,xBounds)fismat = genfis2(Xin,Xout,radii,xBounds,options)说明 Xin是一个矩阵,它的每一行包含一个数据点的输入值;Xout是一个矩阵,它的每一行包含一个数据点的输出值;randi是一个向量,它指定一个聚类中心在一个数据维上作用的范围,这里假定数据位于一个单位超立方体内:xBounds 是一个2×N可选矩阵,它用于指定如何将Xin和Xout中的数据映射到一个超立方体内,这里是数据的维数(行数);options是一个可选向量,它指定的值用于覆盖算法参数的缺省值。
例6-20fismat = genfis2(Xin,Xout,0.5)这是使用此函数所需的最小变量数。
这里对所有数据维指定0.5的作用范围。
fismat = genfis2(Xin,Xout,[0.5 0.25 0.3])这里假定组合的维数是3。
假设Xin有两维、Xout有一维,那么,0.5和0.25是Xin数据维中每一维的作用范围,0.3是Xout数据维的作用范围。
fismat = genfis2(Xin,Xout,0.5,[-10 -5 0; 10 5 20])这里指定了如何将Xin和Xout中的数据规范化为[0 1]区间中的值来进行处理。
假设Xin有两维、Xout有一维,那么Xin 第一列中的数据是从[-10 +10]比例变换后的值,Xin第二列中的数据是从[-5 +5]比例变换后的值,Xout中的数据是从[0 20]比例变换后的值。
6.2.3 生成一个FIS输出曲面函数gensurf格式 gensurf(fis) %使用前两个输入和第一个输出来生成给定模糊推理系统(fis)的输出曲面gensurf(fis,inputs,output) %使用分别由向量input和标量output给定的输入(一个或两个)和输出(只允许一个)来生成一个图形。
gensurf(fis,inputs,output,grids) %指定X(第一、水平)和Y(第二、垂直)方向的网格数。
如果是二元向量,X和Y 方向上的网格可以独立设置。
gensurf(fis,inputs,output,grids,refinput) %用于多于两个的输入,refinput向量的长度与输入相同:·将对应于要显示的输入的refinput项,设置为NaN;·对其它输入的固定值设置为双精度实标量。
[x,y,z]=gensurf(…) %返回定义输出曲面的变量并且删除自动绘图。
例6-21>>a = readfis('tipper');>>gensurf(a)结果为图6-22。
图6-226.2.4 将mamdan型FIS转换为Sugeno FIS函数mam2sug格式 sug_fis=mam2sug(mam_fis)说明该函数将一个mamdani型FIS结构(不必是单输出)mam_fis转化为一个sugeno型结构sug_fis。
返回的sugeno 型系统具有常值输出隶属度函数。
这些常值由原来mamdani型系统的后件的隶属度函数的面积中心法来确定。
前件仍保6.2.5 完成模糊推理计算函数evalfis格式 output= evalfis(input,fismat)output= evalfis(input,fismat, numPts)[output, IRR, ORR, ARR]= evalfis(input,fismat)[output, IRR, ORR, ARR]= evalfis(input,fismat, numPts)说明 input:指定输入值的一个数或一个矩阵,如果输入是一个M×N矩阵,其中N是输入变量数,那么evalfis使用input的每一行作为一个输入向量,并且为变量output返回M×L矩阵,该矩阵每一行是一个向量并且L是输出变量数;fismat:要计算的一个FIS结构;numPts:一个可选变量,它表示在输入或输出范围内的采样点数,在这些点上计算隶属函数,如果不使用此变量,就使用101点的缺省值。