电子技术习题解答第章触发器和时序逻辑电路及其应用习题解答
- 格式:doc
- 大小:799.00 KB
- 文档页数:12
1第8章 触发器和时序逻辑电路——基本习题解答8.4如果D 触发器外接一个异或门,则可把D 触发器转换成T 触发器,试画出其逻辑图。
解:Q n +1=D=T ⊕Q n 故D =T ⊕Q n 如题8.4图所示。
题8.4.图8.5试用T 触发器和门电路分别构成D 触发器和JK 触发器。
解:(1)T 触发器构成D 触发器Q n +1=D =T ⊕Q n ∴T =D ⊕Q n 如题8.5(a )图所示。
题8.5(a )图(2)T 触发器构成JK 触发器Q n +1=n n n n Q K Q J Q T Q T +=+=T ⊕Q n ∴T =n n n n n KQ Q J Q Q K Q J +=⊕+)(如题8.5(b )图所示。
题8.5(b )图8.6逻辑电路如题8.6图(a )所示,设初始状态Q 1=Q 2=0,试画出Q 1和Q 2端的输出波形。
时钟脉冲C 的波形如题8.6图(b )所示,如果时钟频率是4000Hz ,那么Q 1和Q 2波形的频率各为多少?题8.6图(a ) 题8.6图(b )解:JK 触发器构成了T ′触发器,逻辑电路为异步加法计数,Q 1和Q 2端的输出波形如题CP228.6图(c )所示。
Q 1输出波形为CP 脉冲的二分频,Q 2输出波形为CP 脉冲的四分频。
如果CP 脉冲频率为4000Hz ,则Q 1波形的频率是2000Hz ;Q 2波形的频率是1000Hz 。
题8.6图(c )8.8试列出题8.8图所示计数器的状态表,从而说明它是一个几进制计数器。
题8.8图解:F 0:J 0=21Q Q ,K 0=1F 1:J 1=Q 0,K 1=20=Q 0+Q 2 F 2:QJ 2=K 2=1假设初态均为0,分析结果如题8.8图(a )所示,Q 2Q 1Q 0经历了000-001-010-011-100-101-110七种状态,因此构成七进制异步加法计数器。
题8.8图(a )8.9试用主从型JK 触发器组成两位二进制减法计数器,即输出状态为“11”、“10”、“01”、Q Q Q3“00”。
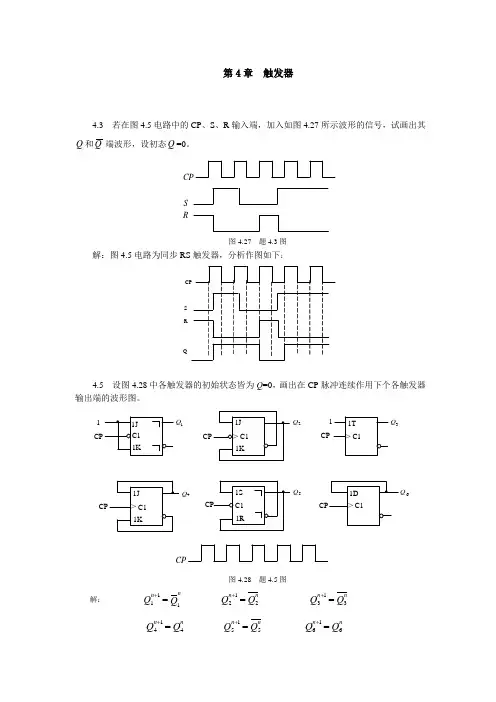
第4章 触发器4.3 若在图4.5电路中的CP 、S 、R 输入端,加入如图4.27所示波形的信号,试画出其Q 和Q 端波形,设初态Q =0。
SRCP图4.27 题4.3图解:图4.5电路为同步RS 触发器,分析作图如下:S RQ4.5 设图4.28中各触发器的初始状态皆为Q =0,画出在CP 脉冲连续作用下个各触发器输出端的波形图。
Q 11CPQ 3CPCPQ 2Q 6Q 4Q 5CP图4.28 题4.5图解:Q Q nn 111=+ Q Q n n 212=+ Q Q nn 313=+Q Q n n 414=+ Q Q n n 515=+ Q Q nn 616=+Q 1CP Q 2Q 3Q 4Q 5Q64.6 试写出 图4.29(a)中各触发器的次态函数(即Q 1 n+1 、 Q 2 n+1与现态和输入变量之间的函数式),并画出在图4.29(b )给定信号的作用下Q 1 、Q 2的波形。
假定各触发器的初始状态均为Q =0。
1A BCP>1D C1=1A BQ 1Q 2Q 2(a)BA(b)图4.29题4.6图解:由图可见:Q B A AB Q n n 111)(++=+ B A Q n ⊕=+12B A Q 2Q 14.7 图4.30(a )、(b )分别示出了触发器和逻辑门构成的脉冲分频电路,CP 脉冲如图4.30(c )所示,设各触发器的初始状态均为0。
(1)试画出图(a )中的Q 1、Q 2和F 的波形。
(2)试画出图(b )中的Q 3、Q 4和Y 的波形。
Y(b )(c )CPQ 1Q 2(a )图4.30 题4.7图解: (a )Q Q nn 211=+ QQ nn 112=+ Q F 1CP ⊕= R 2 = Q 1 低电平有效CPQ 1Q 2F(b )Q Q Q n n n 4313=+ Q Q Q n n n 4314=+ Q Q Y nn43=CP 3= CP 上降沿触发 CP 4= CP 下降沿触发CPQ 3Q 4Y4.8 电路如图4.31所示,设各触发器的初始状态均为0。

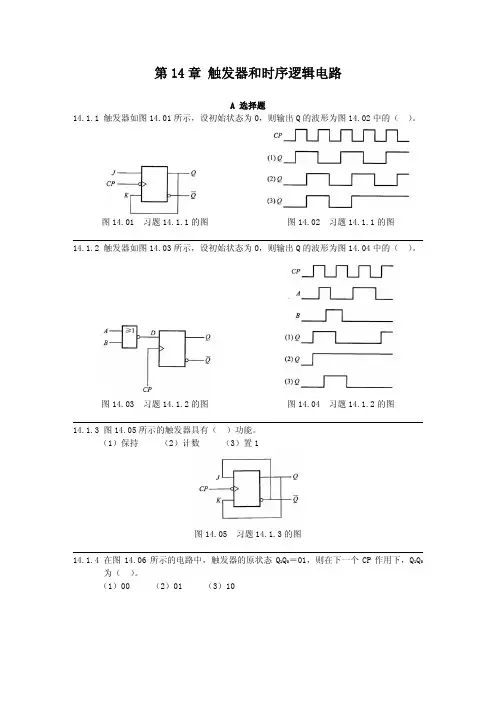
第14章 触发器和时序逻辑电路A 选择题14.1.1 触发器如图14.01所示,设初始状态为0,则输出Q的波形为图14.02中的( )。
图14.01 习题14.1.1的图 图14.02 习题14.1.1的图14.1.2 触发器如图14.03所示,设初始状态为0,则输出Q的波形为图14.04中的( )。
图14.03 习题14.1.2的图 图14.04 习题14.1.2的图14.1.3 图14.05所示的触发器具有( )功能。
(1)保持 (2)计数 (3)置1图14.05 习题14.1.3的图14.1.4 在图14.06所示的电路中,触发器的原状态Q1Q0=01,则在下一个CP作用下,Q1Q0为( )。
(1)00 (2)01 (3)10图14.06 习题14.1.4的图 图14.07 习题14.1.5的图14.1.5在图14.07所示的电路中,触发器的原状态Q1Q0=00,则在下一个CP作用下,Q1Q0为( )。
(1)00 (2)01 (3)1014.3.1 图14.08所示的是( )计数器。
(1)七进制 (2)八进制 (3)九进制图14.08 习题14.3.1的图14.4.1 由555定时器组成的单稳态触发器如图14.4.2(a)所示,若加大电容C的电容值,则( )。
(1)增大输出脉冲u0的幅度(2)增大输出脉冲u0的宽度(3)对输出脉冲u0无影响14.4.2 由555定时器组成的多谐振荡器如图14.4.3(a)所示,欲使振荡频率增高,则可( )。
(1)减小C (2)增大R1,R2 (3)增大U CCB基本题14.1.6 当基本RS触发器D R和D S端加上图14.09所示的波形时,试画出Q端的输出波形。
设初始状态为0和1两种情况。
14.1.7 当可控RS触发器CP,S和R端加上图14.10所示的波形时,使画出Q端的输出波形。
设初始状态为0和1两种情况。
图14.09 习题14.1.6的图 图14.10 习题14.1.7的图14.1.8 当主从型JK触发器的CP,J、K端分别加上图14.11所示的波形时,试画出Q端的输出波形。

第十三章触发器和时序逻辑电路13.1重点内容提要时序逻辑电路由组合逻辑电路和具有记忆作用的触发器构成。
时序逻辑电路的特点是:其输出不仅仅取决于电路的当前输入,而且还与电路的原来状态有关。
1.双稳态触发器双稳态触发器的特点:1).有两个互补的输出端Q 和Q。
2).有两个稳定状态。
“1”状态和“0” 状态。
通常将Q = 1和Q= 0 称为“1”状态,而把Q = 0和Q = 1称为“0” 状态。
3).当输入信号不发生变化时,触发器状态稳定不变。
4).在一定输入信号作用下,触发器可以从一个稳定状态转移到另一个稳定状态。
按其逻辑功能,触发器可分为:RS触发器,JK触发器、D触发器、T触发器和T’触发器。
各时钟控制触发器的逻辑符号和逻辑功能见表13.1.1:把一种已有的触发器通过加入转换逻辑电路,可以转换成为另一种功能的触发器。
2.同步时序逻辑电路的分析同步时序逻辑电路的分析步骤如下:1.由给定的逻辑电路图写出下列各逻辑方程式: (1)各触发器的特性方程。
(2)各触发器的驱动方程。
(3)时序电路的输出方程。
2.将驱动方程代入相应触发器的特性方程,求得电路的状态方程(或次态方程)。
3.根据状态方程和输出方程,列出该时序电路的状态表,画出状态转换图或时序图。
4.根据电路的状态转换图说明该时序逻辑电路的逻辑功能。
3.典型的时序逻辑电路在数字系统中,最典型的时序逻辑电路是寄存器和计数器。
1)寄存器寄存器是用来存储数据或运算结果的一种常用逻辑部件。
寄存器的主要组成部分是在双稳态触发器基础上加上一些逻辑门构成。
按功能分,寄存器分为数码寄存器和移位寄存器。
移位寄存器是既能寄存数码,又能在时钟脉冲的作用下使数码向高位或向低位移动的逻辑功能部件。
通常有左移寄存器、右移寄存器、双向移位寄存器和循环移位寄存器。
移位寄存器可实现数据的串行、并行转换,数据的运算和数据的处理等。
2)计数器计数器是一种对输入脉冲数目进行计数的时序逻辑电路,被计数的脉冲信号称为计数脉冲。
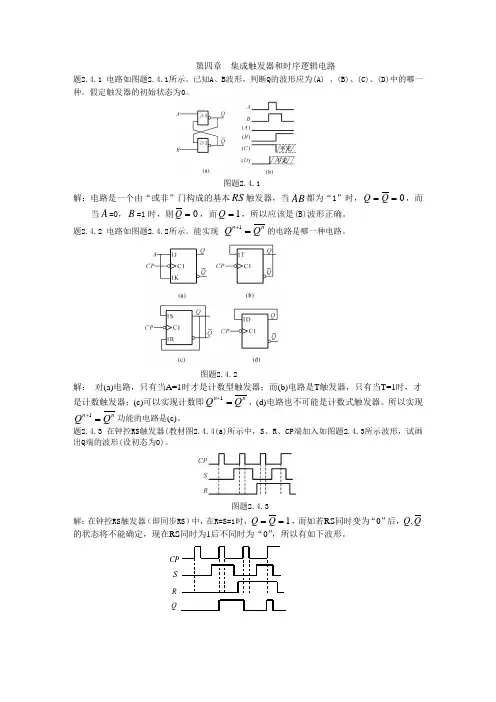
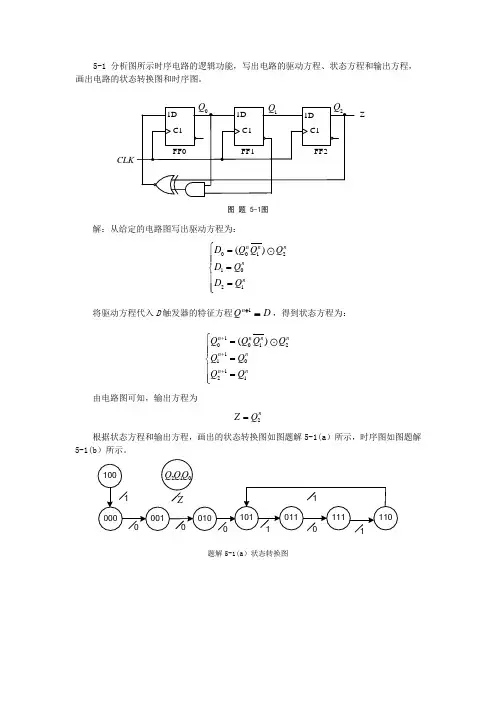
5-1 分析图所示时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图和时序图。
CLKZ图 题 5-1图解:从给定的电路图写出驱动方程为:00121021()n n nn n D Q Q Q D Q D Q ⎧=⎪⎪=⎨⎪=⎪⎩将驱动方程代入D 触发器的特征方程D Qn =+1,得到状态方程为:10012110121()n n n n n n n n Q Q Q Q Q Q Q Q +++⎧=⎪⎪=⎨⎪=⎪⎩由电路图可知,输出方程为2nZ Q =根据状态方程和输出方程,画出的状态转换图如图题解5-1(a )所示,时序图如图题解5-1(b )所示。
题解5-1(a )状态转换图1Q 2/Q ZQ题解5-1(b )时序图综上分析可知,该电路是一个四进制计数器。
5-2 分析图所示电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图。
A 为输入变量。
YA图 题 5-2图解:首先从电路图写出驱动方程为:()0110101()n n n n nD AQ D A Q Q A Q Q ⎧=⎪⎨==+⎪⎩将上式代入触发器的特征方程后得到状态方程()101110101()n n n n n n nQ AQ Q A Q Q A Q Q ++⎧=⎪⎨==+⎪⎩电路的输出方程为:01n nY AQ Q =根据状态方程和输出方程,画出的状态转换图如图题解5-2所示YA题解5-2 状态转换图综上分析可知该电路的逻辑功能为:当输入为0时,无论电路初态为何,次态均为状态“00”,即均复位;当输入为1时,无论电路初态为何,在若干CLK 的作用下,电路最终回到状态“10”。
5-3 已知同步时序电路如图(a)所示,其输入波形如图 (b)所示。
试写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图和时序图,并说明该电路的功能。
X(a) 电路图1234CLK5678X(b)输入波形 图 题 5-3图解:电路的驱动方程、状态方程和输出方程分别为:00101100011011011, ,n n n n n n n n n nJ X K X J XQ K XQ X Q XQ XQ XQ Q XQ XQ XQ Y XQ ++⎧==⎪⎨==⎪⎩⎧=+=⎪⎨⎪=+=+⎩= 根据状态方程和输出方程,可分别做出1110,n n Q Q ++和Y 的卡诺图,如表5-1所示。

第5章 半导体器件习题选解 P148-1505.2.1 如题5.2.1图所示电路中,试求下列几种情况下输出端Y 的电位V Y 及各元件中通过的电流:(1)V A =V B =0V ;(2)V A =+3V ,V B =0V ;(3)V A = V B = +3V ;二极管的正向压降可忽略不计。
解:(1)当V A =V B =0时,因二极管正向偏置,而使D A 、D B 处于导通状态,电流相等,电阻R 上的电流为:mA I I I DB DA R 07.39.312==+=,输出端V Y =0V 。
(2)当V A =3V,V B =0时,因二极管D B 正向偏置,而使其处于导通状态,即D B 导通,同时使D A 反向偏置,而使D A 截止,则流过D A 的电流为0;流过D B 和电阻R 上的电流相等,即:mA I I DB R 07.39.312===。
(3)当V A =V B =+3V 时,因二极管正向偏置,而使D A 、D B 处于导通状态,电流相等,电阻R 上的电流为:mA I I I DB DA R 3.29.3312=-=+=,输出端V Y = +3V 。
题5.2.1图5.2.3 题5.2.3图所示,E=5V ,,sin 10tV u i ω= 二极管的正向压降可忽略不计,试分别画出输出电压0u 的波形。
解:利用二极管的单向导电性,分析各个电路,所以它们的输出电压波形分别为:(a)、(b)对应的波形为(a );(c)、(d)对应的波形为(b )。
题5.2.3图5.3.1 现有两个稳压管D Z1、D Z2,稳定电压分别为4.5V 和9.5V ,正向电压均为0.5V ,试求如题5.3.1图所示各电路中的输出电压U 0。
解:(a )图:VU U U Z Z 145.95.4210=+=+=(b )图:V U 00= ,因为外加电压小于两个稳压管的稳压值。
(c )图:V U 15.05.00=+=, 两个稳压管的均正向导通。


第8章 触发器和时序逻辑电路及其应用习题解答8.1 已知基本RS 触发器的两输入端D S 和D R 的波形如图8-33所示,试画出当基本RS 触发器初始状态分别为0和1两种情况下,输出端Q的波形图。
图8-33 习题8.1图解:根据基本RS 触发器的真值表可得:初始状态为0和1两种情况下,Q的输出波形分别如下图所示:习题8.1输出端Q的波形图8.2 已知同步RS 触发器的初态为0,当S 、R 和CP 的波形如图8-34所示时,试画出输出端Q的波形图。
图8-34 题8.2图解:根据同步RS 触发器的真值表可得:初始状态为0时,Q的输出波形分别如下图所示:习题8.2输出端Q的波形图8.3 已知主从JK触发器的输入端CP、J和K的波形如图8-35所示,试画出触发器初始状态分别为0时,输出端Q的波形图。
图8-35 习题8.3图解:根据主从JK触发器的真值表可得:初始状态为0情况下,Q的输出波形分别如下图所示:习题8.3输出端Q的波形图8.4 已知各触发器和它的输入脉冲CP的波形如图8-36所示,当各触发器初始状态均为1时,试画出各触发器输出Q端和Q端的波形。
图8-36 习题8.4图解:根据逻辑图及触发器的真值表或特性方程,且将驱动方程代入特性方程可得状态方程。
即:(a )J =K =1;Qn +1=n Q,上升沿触发 (b)J =K =1;Qn +1=n Q, 下降沿触发 (c)K =0,J =1;Qn +1=J n Q+K Qn =1,上升沿触发 (d)K =1,J =n Q;Qn +1=J n Q+K Qn =n Qn Q+0·Qn =n Q,上升沿触发 (e)K =Qn ,J =n Q;Qn +1=J n Q+K Qn =n Qn Q+0=n Q,上升沿触发 (f)K =Qn ,J =n Q;Qn +1=J n Q+K Qn =n Qn Q+0=n Q,下降沿触发, 再根据边沿触发器的触发翻转时刻,可得当初始状态为1时,各个电路输出端Q的波形分别如图(a )、(b )、(c )、(d )、(e )和(f )所示,其中具有计数功能的是:(a )、(b )、(d )、(e )和(f )。
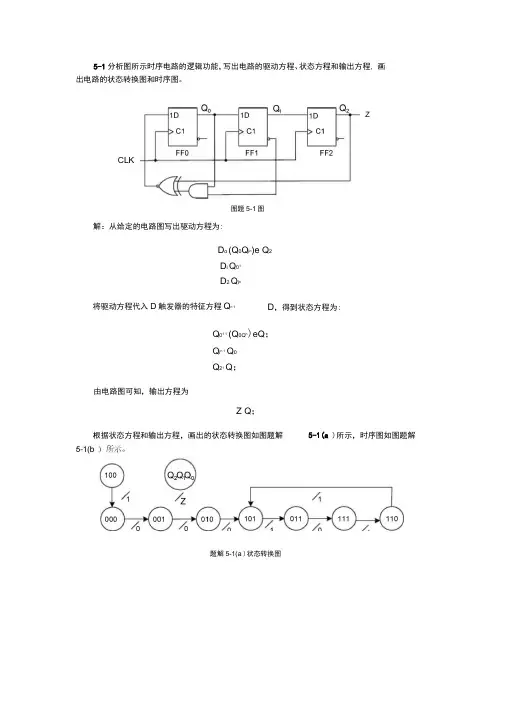
5-1分析图所示时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程, 画出电路的状态转换图和时序图。
解:从给定的电路图写出驱动方程为:D o (Q 0Q i n)e Q 2D i Q 01D 2 Q i nQ 01 1(Q 0Q n)eQ ;Q i n 1Q 0Q 21Q ;由电路图可知,输出方程为Z Q ;CLK将驱动方程代入D 触发器的特征方程Q n 1D ,得到状态方程为:5-1(a )所示,时序图如图题解Z图题5-1图根据状态方程和输出方程,画出的状态转换图如图题解题解5-1(a )状态转换图综上分析可知,该电路是一个四进制计数器。
5-2分析图所示电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图。
A 为输入变量。
解:首先从电路图写出驱动方程为:D o A& D i A Qg :A (Q : Q i n)将上式代入触发器的特征方程后得到状态方程Q 0 1AQ :Q :1 AQ 0Q :A (Q nQ :)电路的输出方程为:CLKQ i12345——-A1 11 t----------- 1------------ 1|| 1 » 1 1 1----------- 1 ---------- 1 --------------►CLK0 Q 2/Z 仝题解5-1(b )时序图0 Q o 胃AY图题5-2图丫AQoQ;根据状态方程和输出方程,画出的状态转换图如图题解5-2 所示综上分析可知该电路的逻辑功能为:当输入为0时,无论电路初态为何,次态均为状态" 00”,即均复位;当输入为1时,无论电路初态为何,在若干CLK 的作用下,电路最终回到状态“10”。
5-3已知同步时序电路如图(a )所示,其输入波形如图 (b )所示。
试写出电路的驱动方 程、状态方程和输出方程,画出电路的状态转换图和时序图,并说明该电路的功能。
CLK 1 2345678(b )输入波形 图题5-3图解:电路的驱动方程、状态方程和输出方程分别为:J 。
第14章触发器和时序逻辑电路一、选择题:1、相同计数器的异步计数器和同步计数器相比,一般情况下()A。
驱动方程简单 B. 使用触发器个数少C. 工作速度快 D。
以上都不对2、n级触发器构成的环形计数器,其有效循环的状态数是( )A. n个 B。
2个 C. 4个 D. 6个3、下图所示波形是一个( )进制加法计数器的波形图.试问它有( )个无效状态。
A .2; B. 4 ; C。
6; D. 12PQ1Q2Q34、设计计数器时应选用( )。
A.边沿触发器 B.基本触发器C.同步触发器 D.施密特触发器5、一块7490十进制计数器中,它含有的触发器个数是( )A。
4 B. 2 C。
1 D. 66、n级触发器构成的扭环形计数器,其有效循环的状态数是( )A。
2n个 B。
n个 C. 4个 D。
6个7、时序逻辑电路中一定包含()A。
触发器 B。
组合逻辑电路 C.移位寄存器 D。
译码器8、用n个触发器构成计数器,可得到的最大计数长度为()A. 2n B。
2n C。
2n D.n9、有一个移位寄存器,高位在左,低位在右,欲将存放在其中的二进制数乘上(4)10,则应将该寄存器中的数( )A。
右移二位 B.左移一位 C. 右移二位 D.左移一位10、某时序逻辑电路的状态转换图如下,若输入序列X=1001时,设起始状态为S1,则输出序列Z=() X/Z 0/11/0 S1 S2 0/01/1A。
0101 B。
1011 C。
0111 D。
100011、、一位8421BCD码计数器至少需要( )个触发器A。
4 B. 3 C.5 D.1012、利用中规模集成计数器构成任意进制计数器的方法有( ABC )A.复位法B.预置数法 C。
级联复位法13、在移位寄存器中采用并行输出比串行输出( )。
A.快 B。
慢 C.一样快 D。
不确定14、用触发器设计一个24进制的计数器,至少需要( )个触发器。
A。
5 B。
4 C。
《时序逻辑电路》练习题及答案CP图P6J6・1Q;Q;Q;■y000Qr Y0 0 0 0 0 1 0 1 0 0 0 0 0 10 0 1 0 1 0 0 1 0 1 0 1 1 10 1 0 0 1 1 0 1 1 0 0 1 0 10 1 1 1 0 0 0 1 1 1 0 0 1 1电路的逻辑功能:是一个五进制计数器,计数顺序是从0到4循环。
[6.2]试分析图P6-2时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程, 画出电路的状态转换图。
A为输入逻辑变量。
[6J]分析图P6・l时序电路的逻辑功能•写出电路的驱动方程、状态方程和输出方程, 画出电路的状态转换图,说明电路能否自启动。
Q11J >C1IK尸Y>C1L 1K>C1Q3驱动方程:人=匕=@丿2 = K? =Qi, 丿3=Q I Q,K3 = 03 ,Y=2状态方程:e笄=00"+迓㊉0:Q T= .输出方程:由状态方程可得状态转换表,如表6・1所示:所示。
电路可以自启动。
由状态转换表可得状态转换图,如图A&1A Y图P6-2CP图P6・3【解]___人=223, K] =1 ;丿2 =01,心=0仪3; Q 置=瓯・a : er* =aa+aaQ ; y= Q2Q3电路的状态转换图如图A6・3所示,电路能够自启动。
Q3Q2Q1 /¥/0/O 图 A6-3[64] 分析图P6・4给出的时序电路,画出电路的状态转换图.检査电路能否自启动, 说明电路实现的功能。
A 为输入变量。
【解1 驱动方程:A =.状态方程:QT = A© , 输出方程:丫 =辺2餌=A^©=A(@+0)由状态方程可得状态转换表,如表6-2所示:由状态转换表 可得状态转换图,如图A&2所示0电路的逻辑功能是:判断A 是否连续输入四个和四个以上“T' 信号,是则YH,否则Y=0,Q2Q1 A/YA00 Q70 0 0 0 1 0 0 0 1 1 0 0 0 1 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 1 1 1 1 1 0 0 1 1 00 1 0 1 0 10 0[6.3] 试分析图P6・3时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图,检査电路能否自启动0r°>ci一 IKr°t>ci丿3 = 2121* K3 = Q](2r' = aaa+aa1/1表6・YrHhCl L IK101/oZo□0Dll/O□IZo/I LIO100D007 r4>cirvci °2f >C1 -IKf=>Cl L-I IKCP图P64【解]__丿广K| = 1,代入到特性方程刖=W+K Q :.得:er' =:A=K2=A + a,代入到特性方程2賈=厶02" +斤20;,得: y== A ae,+AQQ由状态办程可得H 状态转换表,如髮6・4所示,状态转换图如图A6・4所示。
第21章 触发器和时序逻辑电路191、触发器按其工作状态是否稳定可分为( b )。
(a)RS 触发器,JK 触发器,D 触发器,T 触发器;(b)双稳态触发器,单稳态触发器,无稳态触发器;(c)主从型触发器,维持阻塞型触发器。
192、逻辑电路如图所示,当A=“1”时,基本RS 触发器( c )。
(a)置“1”; (b)置“0”; (c)保持原状态。
A193、 逻辑电路如图所示,分析C ,S ,R 的波形,当初始状态为“0”时,输出Q 是“0”的瞬间为( c )。
(a)1t ; (b)2t ; (c)3t 。
C S Rt 1t 2t3194、 某主从型JK 触发器,当J=K=“1”时,C 端的频率f=200Hz ,则Q 的频率为( c )。
(a)200Hz ; (b)400Hz ; (c)100Hz 。
195、逻辑电路如图所示,当A=“1”时,C 脉冲来到后JK 触发器( a )。
(a)具有计数功能; (b)置“0”; (c)置“1”。
A196、 逻辑电路如图所示,A=“0”时,C 脉冲来到后D 触发器( b )。
(a)具有计数器功能; (b)置“0”; (c)置“1”。
A 197、逻辑电路如图所示,分析C 的波形,当初始状态为“0”时,输出Q是“0”的瞬间为( a )。
(a) 1t ; (b)2t ; (c)3t 。
C t 1t 2t 3198、逻辑电路如图所示,它具有( a )。
(a)D 触发器功能; (b)T 触发器功能; (c)T'触发器功能。
199、逻辑电路如图所示,它具有( b )。
(a)D 触发器功能; (b)T 触发器功能;(c)T'触发器功能。
200、时序逻辑电路与组合逻辑电路的主要区别是( c )。
(a)时序电路只能计数,而组合电路只能寄存;(b)时序电路没有记忆功能,组合电路则有;(c)时序电路具有记忆功能,组合电路则没有。
201、寄存器与计数器的主要区别是( b )。
第8章 触发器和时序逻辑电路及其应用习题解答8.1 已知基本RS 触发器的两输入端D S 和D R 的波形如图8-33所示,试画出当基本RS 触发器初始状态分别为0和1两种情况下,输出端Q的波形图。
图8-33 习题8.1图解:根据基本RS 触发器的真值表可得:初始状态为0和1两种情况下,Q的输出波形分别如下图所示:习题8.1输出端Q的波形图8.2 已知同步RS 触发器的初态为0,当S 、R 和CP 的波形如图8-34所示时,试画出输出端Q的波形图。
图8-34 题8.2图解:根据同步RS 触发器的真值表可得:初始状态为0时,Q的输出波形分别如下图所示:习题8.2输出端Q的波形图8.3 已知主从JK触发器的输入端CP、J和K的波形如图8-35所示,试画出触发器初始状态分别为0时,输出端Q的波形图。
图8-35 习题8.3图解:根据主从JK触发器的真值表可得:初始状态为0情况下,Q的输出波形分别如下图所示:习题8.3输出端Q的波形图8.4 已知各触发器和它的输入脉冲CP的波形如图8-36所示,当各触发器初始状态均为1时,试画出各触发器输出Q端和Q端的波形。
图8-36 习题8.4图解:根据逻辑图及触发器的真值表或特性方程,且将驱动方程代入特性方程可得状态方程。
即:(a )J =K =1;Qn +1=n Q,上升沿触发 (b)J =K =1;Qn +1=n Q, 下降沿触发 (c)K =0,J =1;Qn +1=J n Q+K Qn =1,上升沿触发 (d)K =1,J =n Q;Qn +1=J n Q+K Qn =n Qn Q+0·Qn =n Q,上升沿触发 (e)K =Qn ,J =n Q;Qn +1=J n Q+K Qn =n Qn Q+0=n Q,上升沿触发 (f)K =Qn ,J =n Q;Qn +1=J n Q+K Qn =n Qn Q+0=n Q,下降沿触发, 再根据边沿触发器的触发翻转时刻,可得当初始状态为1时,各个电路输出端Q的波形分别如图(a )、(b )、(c )、(d )、(e )和(f )所示,其中具有计数功能的是:(a )、(b )、(d )、(e )和(f )。
各个电路输出端Q的波形与相应的输出端Q的波形相反。
习题8.4各个电路输出端Q的波形图8.5 已知如图8-37所示的主从JK触发器和它的输入端CP的波形图,当各触发器的初始状态均为1时,试画出输出端Q1和Q2的波形图?若时钟脉冲C的频率为200Hz,试问输出端Q1和Q2波形的频率各为多少?图8-37 习题8.5图解:根据逻辑图可得驱动方程,即:J1=K1=1;J2=K2=1。
根据JK触发器的翻转条件、驱动方程和真值表,可直接画出当初始状态为1时,Q1和Q2的输出波形分别如图所示。
从波形图可看出,Q1的周期为C的两倍,Q2的周期为Q1的两倍,若C的频率为200Hz,则Q1的频率为100Hz,Q2的频率为50Hz。
习题8.5电路输出端Q1和Q2的波形图8.6 逻辑电路图如图8-38(a)所示,输入信号CP、A和B的波形图如图8-38(b)所示的,设触发器的初始状态为Q=0。
试写出它的特性方程,并画出输出Q端的波形。
(a)(b)图8-38 习题8.6图Q+KQn。
解:根据逻辑图可得驱动方程,即:J=K=A B。
特性方程为:Qn+1=J n当初始状态为0时,Q的输出波形如图所示。
习题8.6电路输出端Q的波形图8.7 已知维持阻塞D触发器波形的输入CP和D的波形图如图8-39所示,设触发器的初始状态为Q=0。
试画出输出端Q和Q的波形。
图8-39 习题8.7图解:根据D触发器的翻转条件和真值表,可直接画出当初始状态为0时,输出端Q和Q 的波形分别如图所示。
习题8.7电路输出端Q和Q的波形图8.8 如图8-40(a)所示,F1是D触发器,F2是JK触发器,CP和A的波形如图8-40(b)所示,设各触发器的初始状态为Q=0。
试画出输出端Q1和Q2的波形。
(a)(b)图8-40 习题8.8图解:根据逻辑图可得驱动方程,即:D=A;J=K=Q1。
根据D、JK触发器的翻转条件、驱动方程和真值表,可直接画出当初始状态为0时,Q1和Q2的输出波形分别如图所示。
习题8.8电路输出端Q1和Q2的波形图8.9 分析如图8-41所示电路的逻辑功能,设各触发器的初始状态为Q=0。
写出电路的输出方程方程和画出时序图。
图8-41 习题8.9图解:(1)根据逻辑图列写输出方程:CO =0n Q2nQ根据逻辑图列写各个触发器的驱动方程:J 0=K 0=1;J 1=0n Q2n Q、K 1=0n Q;J 2=0n Q1n Q 、K 2=0n Q。
将驱动方程代入特性方程可得状态方程:10n +Q=0n Q,11n +Q=0n Q1n Q2n Q+0n Q1n Q,12n +Q=0n Q1n Q2n Q+0n Q2n Q (2)将2n Q1n Q0nQ所有初态的组合代入状态方程进行状态计算,并编制状态转换表如表所示。
(3):由状态转换表可直接画出时序图如图所示。
从上述分析可知,其逻辑功能为同步五进制加法计数器。
习题8.9的状态转换表 习题8.9的时序图 8.10 分析如图8-42所示电路的逻辑功能,设各触发器的初始状态为Q=0。
画出时序图。
图8-42 习题8.10图解:(1)从逻辑图列各个触发器驱动方程:D 0=0n Q2n Q;D 1=1n Q;D 2=Q0Q1。
(2)根据D 触发器的翻转条件、驱动方程和真值表,可直接画出时序图如图所示,由时序图可编制状态转换表如表所示。
从上述分析可知,其逻辑功能为异步五进制加法计数器。
习题8.10的时序图 习题8.10的状态转换表 8.11 分析如图8-43所示电路的逻辑功能,设各触发器的初始状态为Q=0。
写出电路的输出方程和画出时序图。
图8-43 题8.11图解:(1)根据逻辑图列写各个触发器的驱动方程:J 0=2n Q、K 0=1;J 1=K 1=1;J 2=0n Q1nQ 、K 2=1。
将驱动方程代入特性方程可得状态方程:10n +Q=0n Q2n Q,11n +Q=1n Q,12n +Q=0n Q1n Q2n Q (2)将2n Q1n Q0nQ所有初态的组合代入状态方程可直接画出时序图如图所示。
从上述分析可知,其逻辑功能为异步八进制加法计数器。
习题8.11的时序图8.12 试用边沿JK 触发器设计一个同步五进制加法计数器。
解:习题8.9的逻辑图即为同步五进制加法计数器。
8.13 试用边沿D 触发器设计一个同步十进制计数器。
解:根据D 触发器的逻辑功能和同步十进制计数器的工作原理,用边沿D 触发器设计的同步十进制计数器逻辑电路图如图所示。
至于其工作原理读者可自行分析。
习题8.13的逻辑电路图8.14试分别用以下集成计数器设计十二进制计数器。
(1)利用CT74LS161的异步清零功能。
(2)利用CT74LS161和CT74LS163的同步置数功能。
(3)利用CT74LS290的异步清零功能。
解:(1)利用计数器CT74LS161的异步清零功能。
假设CT74LS161的并行输入数据端均接入0000码,即D 3D 2D 1D 0=0000,相当于十进制数的0。
因为要构成十二进制计数器,所以N =12,若反馈数码的十进制数用M 表示,则M =N +0=12,即反馈数码为1100。
所以,我们采用与非门译码且经化简后可得D R =32QQ,且同时令LD =CT T =CT P =1即可。
它的逻辑图如图所示。
至于它的工作原理和时序图这里就不多介绍了。
习题8.14(1)的逻辑图(2)假设CT74LS161的并行输入数据端均接入0001码,即D 3D 2D 1D 0=0001,相当于十进制数的1。
因为要构成十二进制计数器,所以N =12,若反馈数码的十进制数用M 表示,则M =N +1-1=12,即反馈数码为1100。
所以,我们采用与非门译码且经化简后可得LD =32QQ,且同时令D R =CT T =CT P =1即可。
它的逻辑图如图所示。
至于它的工作原理和时序图这里就不多介绍了。
习题8.14(2)的逻辑图(3)因为N =12,且CT74LS290采用异步置零,所以相应的反馈清零码应为1100。
根据CT74LS290型二–五–十进制计数器的逻辑功能可知,我们只要把它的Q3、Q2端分别接在R 0(1)和R 0(2)上,且S 9(1)和S 9(2)同时接地,Q0端接在CP 1上,计数脉冲从CP 0输入即可。
它的逻辑图如图所示。
至于它的工作原理和时序图这里就不多介绍了。
习题8.14(3)的逻辑图8.15试分别用以下集成计数器设计二十四进制计数器。
(1)利用CT74LS161的异步清零功能。
(2)利用CT74LS163的同步清零功能。
(3)利用CT74LS161和CT74LS163的同步置数功能。
(4)利用CT74LS290的异步清零功能。
解:(1)因为M =24,所以24<M <28,即需要两片集成CT74LS161型四位二进制同步计数器,再用异步反馈清零法构成二十四进制计数器。
因为是异步清零,而24对应的二进制数为00011000,所以,可令高位片(Ⅱ)的3210''''Q Q Q Q =0001,低位片(Ⅰ)的Q 3Q 2Q 1Q 0=1000。
在输入第24个计数脉冲CP 时,计数器计到24时,计数器的状态为3210''''Q Q Q Q Q 3Q 2Q 1Q 0=00011000,其反馈清零函数为D 03R '=Q Q ,这时,与非门输出低电平0,使两片CT74LS163同时被清零,从而实现二十四进制计数。
逻辑电路如图所示。
习题8.15(1)的逻辑图(2)因为M =24,所以24<M <28,即需要两片集成CT74LS163型四位二进制同步计数器,再用同步反馈清零法构成二十四进制计数器。
因为是同步清零,所以反馈的状态应是24-1=23,而23对应的二进制数为00010111,所以,可令高位片(Ⅱ)的3210''''Q Q Q Q =0001,低位片(Ⅰ)的Q 3Q 2Q 1Q 0=0111。
当计数器计到23时,计数器的状态为3210''''Q Q Q Q Q 3Q 2Q 1Q 0=00010111,其反馈清零函数为D 0210R '=Q Q Q Q ,这时,与非门输出低电平0,在输入第24个计数脉冲CP 时,使两片CT74LS163同时被清零,从而实现二十四进制计数。
电路如图所示。
习题8.15(2)的逻辑图(3)因为M =24,所以24<M <28,即需要两片集成CT74LS161型四位二进制同步计数器。