2014北京市中考数学几何综合复习

2014年北京市高级中等学校招生考试数学试卷学校姓名准考证号下面各题均有四个选项，其中只有一个．．是符合题意的． 1．2的相反数是A ．2B ．2-C ．12-D ．122．据报道，某小区居民李先生改进用水设备，在十年内帮助他居住小区的居民累计节水300 000吨．将300 000用科学记数法表示应为A ．60.310⨯B ．5310⨯C ．6310⨯D ．43010⨯3．如图，有6张扑克处于，从中随机抽取一张，点数为偶数的概率是A ．16B ．14C ．13D ．124．右图是几何体的三视图，该几何体是A.圆锥B ．圆柱C ．正三棱柱D ．正三棱锥5．某篮球队12名队员的年龄如下表所示：A ．18，19B ．19，19C ．18，19.5D ．19，19.56．园林队在某公园进行绿化，中间休息了一段时间．已知绿化面积S（单位：平方米）与工作时间t （单位：小时）的函数关系的图象如图所示，则休息后园林队每小时绿化面积为 A ．40平方米 B ．50平方米 C ．80平方米D ．100平方米OE DCB A7．如图．O e 的直径AB 垂直于弦CD ，垂足是E ，22.5A∠=︒，4OC =，CD 的长为A ．B ．4C ．D ．88．已知点A 为某封闭图形边界上一定点，动点P 从点A 出发，沿其边界顺时针匀速运动一周．设点P 运动的时间为x ，线段AP 的长为y．表示y 与x 的函数关系的图象大致如右图所示，则该封闭图形可能是AADCBAA二、填空题（本题共16分，每小题4分） 9．分解因式：429______________ax ay -=．10．在某一时刻，测得一根高为1.8m 的竹竿的影长为3m ，同时测得一根旗杆的影长为25m ，那么这根旗杆的高度为 m ．11．如图，在平面直角坐标系xOy 中，正方形OABC 的边长为2．写出一个函数(0)ky k x =≠，使它的图象与正方形OABC 有公共点，这个函数的表达式为 ．12．在平面直角坐标系x Oy 中，对于点()P x y ，，我们把点(11)P y x '-++，叫做点P 的伴随点，已知点1A 的伴随点为2A ，点2A 的伴随点为3A ，点3A 的伴随点为4A ，…，这样依次得到点1A ，2A ，3A ，…，n A ，….若点1A 的坐标为（3，1），则点3A 的坐标为 ，点2014A 的坐标为 ；若点1A 的坐标为（a ，b ），对于任意的正整数n ，点n A 均在x 轴上方，则a ，b 应满足的条件为 .三、解答题（本题共30分，每小题5分）13．如图，点B 在线段AD 上，BC DE ∥，AB ED =，BC DB =. 求证：A E ∠=∠.ECBAD14．计算：11(6π)()3tan30|5--︒+--︒+.15．解不等式1211232x x --≤，并把它的解集在数轴上表示出来.16．已知x y -=2(1)2(2)x x y y x +-+-的值. 17．已知关于x 的方程2(2)20(0)mx m x m -++=≠.（1）求证：方程总有两个实数根；（2）若方程的两个实数根都是整数，求正整数m 的值.18．列方程或方程组解应用题：小马自驾私家车从A 地到B 地，驾驶原来的燃油汽车所需油费108元，驾驶新购买的纯电动车所需电费27元，已知每行驶1千米，原来的燃油汽车所需的油费比新购买的纯电动汽车所需的电费多0.54元，求新购买的纯电动汽车每行驶1千米所需的电费.四、解答题（本题共20分，每小题5分）19．如图，在ABCD Y 中，AE 平分BAD ∠，交BC 于点E ，BF 平分ABC ∠，交AD 于点F ，AE 与BF 交于点P ，连接EF ，PD . （1）求证：四边形ABEF 是菱形；（2）若4AB =，6AD =，60ABC ∠=︒，求tan ADP ∠的值.20．根据某研究院公布的2009~2013年我国成年国民阅读调查报告的部分相关数据，绘制的统计图表如下：下载并打印阅读1.0%手机阅读15.6%电子阅读器阅读2.4%网络在线阅读15.0%图书阅读m %根据以上信息解答下列问题： （1）直接写出扇形统计图中m 的值；（2）从2009到2013年，成年国民年人均阅读图书的数量每年增长的幅度近似相等，估算2014年成年国民年人均阅读图书的数量约为 本；（3）2013年某小区倾向图书阅读的成年国民有990人，若该小区2014年与2013年成年国民的人数基本持平，估算2014年该小区成年国民阅读图书的总数量约为 本.年人均阅读图书数量 F PECBAD图3ABCDE21．如图，AB 是O e 的直径，C 是»AB 的中点，O e 的切线BD 交AC 的延长线于点D ，E是OB 的中点，CE 的延长线交切线BD 于点F ，AF 交O e 于点H ，连接BH . （1）求证：AC CD =； （2）若2OB =，求BH 的长.22．阅读下面材料：小腾遇到这样一个问题：如图1，在ABC △中，点D 在线段BC 上，75BAD ∠=︒，30CAD ∠=︒，2AD =，2BD DC =，求AC 的长．E图2图1AB CD D CB A小腾发现，过点C 作CE AB ∥，交AD 的延长线于点E ，通过构造ACE △，经过推理和计算能够使问题得到解决（如图2）．请回答：ACE ∠的度数为 ，AC 的长为 ． 参考小腾思考问题的方法，解决问题：如图3，在四边形ABCD 中，90BAC ∠=︒，30CAD ∠=︒，75ADC ∠=︒，AC 与BD 交于点E ，2AE =，2BE ED =，求BC 的长．五、解答题（本题共22分，第23题7分，第24题7分，第25题8分）23．在平面直角坐标系xOy 中，抛物线22y x mx n =++经过点A （0，2-），B （3，4）．（1）求抛物线的表达式及对称轴；（2）设点B 关于原点的对称点为C ，点D 是抛物线对称轴上一动点，记抛物线在A ，B 之间的部分为图象G （包含A ，B 两点）．若直线CD 与图象G 有公共点，结合函数图像，求点D 纵坐标t 的取值范围．24．在正方形ABCD 外侧作直线AP ，点B 关于直线AP 的对称点为E ，连接BE DE ，，其中DE 交直线AP 于点F ． （1）依题意补全图1；（2）若20PAB ∠=︒，求ADF ∠的度数；（3）如图2，若4590PAB ︒<∠<︒，用等式表示线段AB FE FD ，，之间的数量关系，并证明．图 1PD CBA A BCDP图 225．对某一个函数给出如下定义：若存在实数0M >，对于任意的函数值y ，都满足M y M -≤≤，则称这个函数是有界函数，在所有满足条件的M 中，其最小值称为这个函数的边界值．例如，下图中的函数是有界函数，其边界值是1．（1）分别判断函数1y x=()0x >和()142y x x =+-<≤是不是有界函数？若是有界函数，求其边界值；（2）若函数1y x =-+()a x b b a ≤≤>，的边界值是2，且这个函数的最大值也是2，求b的取值范围；（3）将函数()210y x x m m =-≤≤≥，的图象向下平移m 个单位，得到的函数的边界值是t ，当m 在什么范围时，满足314t ≤≤？。

ABCEDFGH CHFG EPBDA2014年北京市各城区中考一模数学——几何综合题汇总1、（2014年丰台门头沟一模）24.已知：在△ABC 中，∠ABC =∠ACB =α，点D 是AB 边上任意一点，将射线DC 绕点D 逆时针旋转α与过点A 且平行于BC 边的直线交于点E . （1）如图12-1，当α=60°时，请直接写出线段BD 与AE 之间的数量关系；____ _ （2）如图12-2，当α=45°时，判断线段BD 与AE 之间的数量关系，并进行证明； （3）如图12-3，当α为任意锐角时，依题意补全图形，请直接写出线段BD 与AE 之间的数量关系：_______________________．（用含α的式子表示,其中090a <<）2、（2014年丰台一模）24.在等腰直角△ABC 中，∠BAC=90°，AB=AC ， （1）如图1，点D 、E 分别是AB 、AC 边的中点，AF ⊥BE 交BC 于点F ，连结EF 、CD 交于点H.求证，EF ⊥CD ；（2）如图2，AD=AE ，AF ⊥BE 于点G 交BC 于点F ，过F 作FP ⊥CD 交BE 的延长线于点P ，试探究线段BP,FP,AF 之间的数量关系，并说明理由。

B图12-1B图12-2图12-33、（2014年平谷一模）24．（1）如图1，点E 、F 分别是正方形ABCD 的边BC 、CD 上的点，∠EAF =45°，连接EF ，则EF 、BE 、FD 之间的数量关系是：EF =BE +FD ．连结BD ，交AE 、AF 于点M 、N ，且MN 、BM 、DN 满足222DN BM MN +=，请证明这个等量关系；（2）在△ABC 中， AB =AC ，点D 、E 分别为BC 边上的两点．①如图2，当∠BAC =60°，∠DAE =30°时，BD 、DE 、EC 应满足的等量关系是_________________； ②如图3，当∠BAC =α，(0°<α<90°)，∠DAE =α21时，BD 、DE 、EC 应满足的等量关系是_____________．【参考：1cos sin 22=+αα】A B CEF 图1B CDE 图2AD图3AMN4、（2014年顺义一模）24．已知：如图，MNQ △中，MQ NQ ≠．（1）请你以MN 为一边，在MN 的同侧构造一个 与MNQ △全等的三角形，画出图形，并简要说明构造的方法；（2）参考（1）中构造全等三角形的方法解决下 面问题： 如图，在四边形ABCD 中，180ACB CAD ∠+∠=︒，B D ∠=∠． 求证：CD=AB ．QNMDCBA5、（2014年石景山一模）24．在矩形ABCD 中，AD =12，AB =8，点F 是AD 边上一点，过点F 作∠A F E =∠D F C ，交射线A B 于点E ，交射线C B 于点G ． （1）若FG =_____CFG ∠=︒；（2） 当以F ，G ，C 为顶点的三角形是等边三角形时，画出图形并求GB 的长； （3）过点E 作EH//CF 交射线CB 于点H ，请探究：当GB 为何值时，以F ，H ，E ，C为顶点的四边形是平行四边形．6、（2014年海淀一模）24．在△ABC 中，AB=AC ，将线段AC 绕着点C 逆时针旋转得到线段CD ，旋转角为α，且0180α<<，连接AD 、BD ．（1）如图1，当∠BAC =100°，60α=时，∠CBD 的大小为_________； （2）如图2，当∠BAC =100°，20α=时，求∠CBD 的大小；（3）已知∠BAC 的大小为m （60120m <<），若∠CBD 的大小与（2）中的结果相同，请直接写出α的大小．DCBAABC备用图7、（2014年西城一模）24. 四边形ABCD 是正方形，BEF ∆是等腰直角三角形，90BEF ∠=︒，BE EF =，连接DF ，G 为DF 的中点，连接EG ，CG ，EC 。

2014-2023北京中考真题数学汇编相似三角形②若点C 是弦2AB 的“关联点”，直接写出OC 的长；(2)已知点()0,3M ，5N ⎛⎫ ⎪ ⎪⎝⎭．对于线段MN 上一点S ，存在O 的弦PQ ，使得点S 是弦PQ 的“关联点”，记PQ 的长为t ，当点S 在线段MN 上运动时，直接写出t 的取值范围．（1）比较BAE ∠与CAD ∠的大小；用等式表示线段（2）过点M 作AB 的垂线，交DE 于点7．（2021北京中考真题）如图，O （1）求证：BAD CAD ∠=∠；（2）连接BO 并延长，交AC 于点F ，a 、若12C B 与O 相切，AC 经过点O ，则12C B 、1AC 所在直线为：20y x y ⎧=-⎪⎨=⎪⎩，解得：()12C ，0，∴12OC =，①当S 位于点()0,3M 时，MP 为O 的切线，作PJ OM ⊥∵()0,3M ，O 的半径为1，且MP 为O 的切线，∴OP MP ⊥，∵PJ OM ⊥，∴MPO POJ ∽ ，∴OP OM OJ OP =，即13OJ=，解得13OJ =，∴根据勾股定理得，22223PJ PO OJ =-=，123Q J =根据勾股定理，22111233PQ Q P Q J =+=，同理，2PQ ∴当S 位于点()0,3M 时，1PQ 的临界值为233和263．②当S 位于经过点O 的MN 的垂直平分线上即点K 时，∵点()0,3M ，65,05N ⎛⎫ ⎪ ⎪⎝⎭，∴22955MN OM ON =+=，∴2OK OM ON MN =⨯÷=，又∵O 的半径为1，∴30OKZ ∠=︒，∴三角形OPQ 为等边三角形，∴在此情况下，1PQ =，3PQ =，∴90EQB HQB ∠=∠=︒，由（1）可得ABE ACD ≌，∴ABE ACD ∠=∠，BE CD =，∵AB AC =，∴ABC C ABE ∠=∠=∠，∵BQ BQ =，。

图2图1EDCA2014年北京市各城区中考二模数学——几何综合题24题汇总考点一、平移变换1.平移的概念：在平面内，将一个图形沿某个方向移动一定的距离，这样的图形运动称为平移，平移不改变图形的形状和大小．2．平移的基本性质：由平移的概念知，经过平移，图形上的每一个点都沿同一个方向移动相同的距离，平移不改变图形的形状和大小，因此平移具有下列性质：经过平移，对应点所连的线段平行且相等，对应角相等．例一（2014年平谷二模）（1）如图1，在四边形ABCD 中，∠B =∠C =90°，E 为BC 上一点，且CE =AB ，BE =CD ，连结AE 、DE 、AD ，则△ADE 的形状是_________________________.(2)如图2，在90ABC A ∆∠=︒中，，D 、E 分别为AB 、AC 上的点，连结BE 、CD ，两线交于点P ．①当BD=AC ，CE=AD 时，在图中补全图形，猜想BPD ∠的度数并给予证明． ②当BD CEAC AD==时，BPD ∠的度数____________________．24.（1）等腰直角三角形 ----------------------------------------------------1分（2） 45°. ------------------------------------------------------------2分证明：过B 点作FB ⊥AB ,且FB=AD . ∴90FBD A ∠=∠=︒, ∵BD=AC ，∴△FBD ≌△DAC. ∴∠FDB=∠DCA ，ED=DC ∵∠DCA+∠CDA=90︒，∴∠FDB +∠CDA=90︒，∴∠CDF=90︒，∴∠FCD=∠CFD =45︒． ∵AD =CE ，∴BF =CE∵90FBD A ∠=∠=︒，∴180FBD A ∠+∠=︒. ∴BF ∥EC .∴四边形BECF 是平行四边形． ∴BE ∥FC .∴45BPD FCD ∠=∠=︒.----------------------------------------------6分 （3）60︒． ------------------------------------------------7分练、（2014年海淀二模）24．在ABC △中，90ABC ∠= ，D 为平面内一动点，AD a =，AC b =，其中a ，b 为常数，且a b <.将ABD △沿射线BC 方向平移，得到FCE △，点A 、B 、D 的对应点分别为点F 、C 、E .连接BE .（1）如图1，若D 在ABC △内部，请在图1中画出FCE △；（2）在（1）的条件下，若AD BE ⊥，求BE 的长（用含, a b 的式子表示）； （3）若=BAC α∠，当线段BE 的长度最大时，则BAD ∠的大小为__________；当线段BE 的长度最小时，则BAD ∠的大小为_______________（用含α的式子表示）.图1 备用图24.解:（1）…………………………………………………2分（2）连接BF .∵将ABD △沿射线BC 方向平移，得到FCE △，ABCABC∴AD ∥EF , AD =EF ；AB ∥FC , AB =FC . ∵∠ABC=90°，∴四边形ABCF 为矩形. ∴AC =BF .……………………………………3分∵AD BE ⊥, ∴EF BE ⊥. …………………………………4分∵AD a =，AC b =， ∴EF a =，BF b =.∴BE .………………………………………………………………5分 （3）180α︒-； α.……………………………………………………………7分练、（2014年朝阳二模）24. 已知∠ABC =90°，D 是直线AB 上的点，AD =BC ． （1）如图1，过点A 作AF ⊥AB ，并截取AF =BD ，连接DC 、DF 、CF ，判断△CDF 的形状并证明；（2）如图2，E 是直线BC 上的一点，直线AE 、CD 相交于点P ，且∠APD =45°，求证BD =CE ．24.解：（1）△CDF 是等腰直角三角形．………………1分 证明：∵∠ABC =90°，AF ⊥AB ， ∴∠FAD =∠DBC ． ∵AD =BC ，AF =BD ，∴△FAD ≌△DBC ．∴FD =DC ．…………………………………………2分∠1=∠2．∵∠1+∠3=90°， ∴∠2+∠3=90°．即∠CDF =90°． ……………………………………3分 ∴△CDF 是等腰直角三角形．（2）过点A 作AF ⊥AB ，并截取AF =BD ，连接DF 、CF ．…………………………4分 ∵∠ABC =90°，AF ⊥AB ， ∴∠FAD =∠DBC ． ∵AD =BC ，AF =BD ，∴△FAD ≌△DBC ． ∴FD =DC ，∠1=∠2．∵∠1+∠3=90°， ∴∠2+∠3=90°． 即∠CDF =90°．∴△CDF 是等腰直角三角形．………………………………………………………5分∴∠FCD =∠APD =45°． ∴FC ∥AE ．∵∠ABC =90°，AF ⊥AB ， ∴AF ∥CE ．∴四边形AFCE 是平行四边形．…………………………………………………6分∴AF =CE ．∴BD =CE ．……………………………………………………………………………7分图2图1考点二、轴对称变换 1．轴对称与轴对称图形轴对称：把一个图形沿着某一条直线折叠，如果能够与另一个图形重合，那么就说这两个图形关于这条直线对称，也叫做这两个图形成轴对称，这条直线叫做对称轴，折叠后重合的对应点，叫做对称点.轴对称图形：把一个图形沿着某一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形. 2．轴对称变换的性质①关于直线对称的两个图形是全等图形.②如果两个图形关于某直线对称，对称轴是对应点连线的垂直平分线.③两个图形关于某直线对称，如果它们对应线段或延长线相交，那么交点在对称轴上. ④如果两个图形的对应点连线被同一直线垂直平分，那么这两个图形关于这条直线对称.5.如图,把矩形纸条ABCD 沿EF GH ，同时折叠，B C ，两点恰好落在AD 边的P 点处，若90FPH =∠，8PF =，6PH =，则矩形ABCD 的边BC 长为（ ）.A.20B.22C.24D.30第5题7.如图，AD 是△ABC 的中线，∠ADC＝45°，把△ADC 沿AD 对折，点C 落在点C '的位置，则C B '与BC 之间的数量关系是．8.在Rt ∆ABC 中，∠A <∠B，CM 是斜边AB 上的中线，将∆ACM 沿直线CM 折叠，点A 落在点D 处，如果CD 恰好与AB 垂直，那么∠A 等于度.第7题 第8题10.如图，在∆ABC 中，MN//AC ，直线MN 将∆ABC 分割成面积相等的两部分，将∆BMN 沿直线MN 翻折，点B 恰好落在点E 处，联结AE ，若AE//CN ，则AE:NC=.第10题 第11题11.如图，已知边长为5的等边三角形ABC 纸片，点E 在AC 边上，点F 在AB 边上，沿着EF 折痕，使点A 落在BC 边上的点D 的位置，且,BC ED ⊥则CE 的长是. 12．（2013门头沟二模）如图，将边长为2的正方形纸片ABCD 折叠，使点B落在CD 上，落点记为E （不与点C ，D 重合），点A 落在点F 处，折痕MN 交AD 于点M ，交BC 于点N ．若12CE CD =，则BN 的长是，AM BN的值 等于；若1CE CD n=（2n ≥，且n 为整数）， 则AMBN的值等于 （用含n 的式子表示）．22（2010年北京中考题）小贝遇到一个有趣的问题：在矩形ABCD 中，AD =8cm ，AB =6cm 。

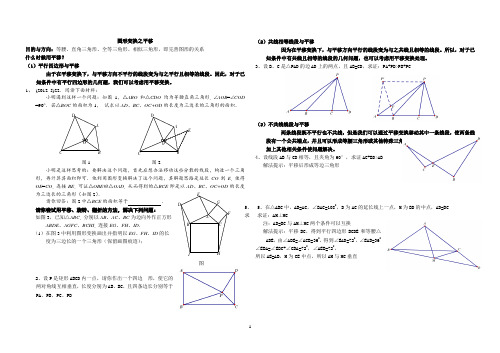
图形变换之平移目的与方向：等腰、直角三角形、全等三角形、相似三角形，即完善图形的关系 什么时候用平移？ （1）平行四边形与平移由于在平移变换下，与平移方向不平行的线段变为与之平行且相等的线段。

因此，对于已知条件中有平行四边形的几何题，我们可以考虑用平移变换。

1、 (2012. 5)22．阅读下面材料：小明遇到这样一个问题：如图1，△ABO 和△CDO 均为等腰直角三角形, ∠AOB =∠COD =90︒．若△BOC 的面积为1， 试求以AD 、BC 、OC+OD 的长度为三边长的三角形的面积．图1 图2小明是这样思考的：要解决这个问题，首先应想办法移动这些分散的线段，构造一个三角形，再计算其面积即可．他利用图形变换解决了这个问题，其解题思路是延长CO 到E , 使得OE =CO , 连接BE , 可证△OBE ≌△OAD , 从而得到的△BCE 即是以AD 、BC 、OC+OD 的长度为三边长的三角形（如图2）．请你回答：图2中△BCE 的面积等于． 请你尝试用平移、旋转、翻折的方法，解决下列问题： 如图3，已知△ABC , 分别以AB 、AC 、BC 为边向外作正方形ABDE 、AGFC 、BCHI , 连接EG 、FH 、ID ．（1）在图3中利用图形变换画出并指明以EG 、FH 、ID 的长度为三边长的一个三角形（保留画图痕迹）；图2、设P 是矩形ABCD 内一点，请你作出一个四边 形，使它的两对角线互相垂直，长度分别为AB 、BC ，且四条边长分别等于PA 、PB 、PC 、PD（2）共线相等线段与平移因为在平移变换下，与平移方向平行的线段变为与之共线且相等的线段。

所以，对于已知条件中有共线且相等的线段的几何问题，也可以考虑用平移变换处理。

3、设B 、C 是△PAD 的边AD 上的两点，且AB=CD ，求证：PA+PD>PB+PC（3）不共线线段与平移两条线段既不平行也不共线，但是我们可以通过平移变换移动其中一条线段，使两条线段有一个公共端点，并且可以形成等腰三角形或其他特殊三角形，再利用特殊三角形的性质再加上其他相关条件使问题解决。

《平面直角坐标系》全章复习与巩固(提高)知识讲解【学习目标】1. 理解平面直角坐标系及象限的概念，并会在坐标系中根据点的坐标描出点的位置、由点的位置写出它的坐标；2. 掌握用坐标系表示物体位置的方法及在物体平移变化前后点坐标的变化；3. 通过学习平面直角坐标系的基础知识,逐步理解平面内的点与有序实数对之间的一一对应关系,进而培养数形结合的数学思想．【知识网络】【要点梳理】要点一、有序数对把一对数按某种特定意义，规定了顺序并放在一起就形成了有序数对，人们在生产生活中经常以有序数对为工具表达一个确定的意思，如某人记录某个月不确定周期的零散收入，可用(13，2000)， (17，190)， (21，330)…，表示，其中前一数表示日期，后一数表示收入，但更多的人们还是用它来进行空间定位，如：(4，5)，(20，12)，(13，2)，…，用来表示电影院的座位，其中前一数表示排数，后一数表示座位号.要点二、平面直角坐标系在平面内画两条互相垂直、原点重合的数轴就组成平面直角坐标系，如下图：要点诠释：（1）坐标平面内的点可以划分为六个区域：x轴，y轴、第一象限、第二象限、第三象限、第四象限，这六个区域中，除了x轴与y轴有一个公共点（原点）外，其他区域之间均没有公共点.（2）在平面上建立平面直角坐标系后，坐标平面上的点与有序数对（x，y）之间建立了一一对应关系，这样就将‘形’与‘数’联系起来，从而实现了代数问题与几何问题的转化. （3）要熟记坐标系中一些特殊点的坐标及特征：① x轴上的点纵坐标为零；y轴上的点横坐标为零．②平行于x轴直线上的点横坐标不相等，纵坐标相等；平行于y轴直线上的点横坐标相等，纵坐标不相等．③关于x轴对称的点横坐标相等，纵坐标互为相反数；关于y轴对称的点纵坐标相等，横坐标互为相反数；关于原点对称的点横、纵坐标分别互为相反数．④象限角平分线上的点的坐标特征：一、三象限角平分线上的点横、纵坐标相等；二、四象限角平分线上的点横、纵坐标互为相反数．注：反之亦成立．（4）理解坐标系中用坐标表示距离的方法和结论：①坐标平面内点P(x，y)到x轴的距离为|y|，到y轴的距离为|x|．② x轴上两点A(x1，0)、B(x2，0)的距离为AB=|x1- x2|；y轴上两点C(0，y1)、D(0，y2)的距离为CD=|y1- y2|．③平行于x轴的直线上两点A(x1，y)、B(x2，y)的距离为AB=|x1- x2|；平行于y轴的直线上两点C(x，y1)、D(x，y2)的距离为CD=|y1- y2|．（5）利用坐标系求一些知道关键点坐标的几何图形的面积：切割、拼补要点三、坐标方法的简单应用1．用坐标表示地理位置(1)建立坐标系，选择一个适当的参照点为原点，确定x轴、y轴的正方向；(2)根据具体问题确定适当的比例尺，在坐标轴上标出单位长度；(3)在坐标平面内画出这些点，写出各点的坐标和各个地点的名称．要点诠释：(1)我们习惯选取向东、向北分别为x轴、y轴的正方向，建立坐标系的关键是确定原点的位置．(2)确定比例尺是画平面示意图的重要环节，要结合比例尺来确定坐标轴上的单位长度．2．用坐标表示平移(1)点的平移点的平移引起坐标的变化规律：在平面直角坐标中，将点(x，y)向右(或左)平移a个单位长度，可以得到对应点(x+a，y)(或(x-a，y))；将点(x，y)向上(或下)平移b个单位长度，可以得到对应点(x，y+b)(或(x，y-b))．要点诠释：上述结论反之亦成立，即点的坐标的上述变化引起的点的平移变换．(2)图形的平移在平面直角坐标系内，如果把一个图形各个点的横坐标都加(或减去)一个正数a，相应的新图形就是把原图形向右(或向左)平移a个单位长度；如果把它各个点的纵坐标都加(或减去)一个正数a，相应的新图形就是把原图形向上(或向下)平移a个单位长度．要点诠释：平移是图形的整体运动，某一个点的坐标发生变化，其他点的坐标也进行了相应的变化，反过来点的坐标发生了相应的变化，也就意味着点的位置也发生了变化，其变化规律遵循：“右加左减，纵不变；上加下减，横不变”．【典型例题】类型一、有序数对1．(某某)如图所示，用点A(3，1)表示放置3个胡萝卜、1棵青菜，用点B(2，3)表示放置2个胡萝卜，3棵青菜．(1)请你写出点C、D、E、F所表示的意义；(2)若一只兔子从点A到达点B(顺着方格线走)，有以下几条路线可以选择：①A→C→D→B；②A→E→D→B；③A→E→F→B，问走哪条路吃到的胡萝卜最多?走哪条路吃到的青菜最多? 【思路点拨】（1）根据问题的“约定”先写出坐标，再回答其实际意义；(2)通过比较三条线路吃胡萝卜、青菜的多少回答问题．【答案与解析】解：(1)因为点A(3，1)表示放置3个胡萝卜、1棵青菜，点B(2，3)表示放置2个胡萝卜、3棵青菜，可得：点C的坐标是(2，1)，它表示放置2个胡萝卜、1棵青菜；点D的坐标是(2，2)，它表示放置2个胡萝卜、2棵青菜；点E的坐标是(3，2)，它表示放置3个胡萝卜、2棵青菜；点F的坐标是(3，3)，它表示放置3个胡萝卜、3棵青菜．(2)若兔子走路线①A→C→D→B，则可以吃到的胡萝卜共有3+2+2+2＝9(个)，吃到的青菜共有1+1+2+3＝7(棵)；走路线②A→E→D→B，则可以吃到的胡萝卜共有3+3+2+2＝10(个)，吃到的青菜共有1+2+2+3＝8(棵)；走路线③A→E→F→B，则可以吃到的胡萝卜共有3+3+3+2＝11(个)，吃到的青菜共有1+2+3+3＝9(棵)；由此可知，走第③条路线吃到的胡萝卜和青菜都最多．【总结升华】由点A（3，1），点B（2，3）表示的意义及已确定平面直角坐标系，可知坐标系中x轴表示胡萝卜的数量，y轴表示青菜的数量．类型二、平面直角坐标系2. (1)若点(5-a，a-3)在第一、三象限的角平分线上，求a的值．(2)已知两点A(-3，m)，B(n，4)，若AB∥x轴，求m的值，并确定n的X围．(3)点P到x轴和y轴的距离分别是3和4，求P点的坐标．【思路点拨】 (1)中在一、三象限的角平分线上的点的横坐标与纵坐标相等；(2)与x轴平行的直线上的点的纵坐标相等；(3)中的点P有多个．【答案与解析】解：(1)因为点(5-a，a-3)在第一、三象限的角平分线上，所以5-a＝a-3，所以a＝4．(2)因为AB∥x轴，所以m＝4，因为A、B两点不重合，所以n≠-3．(3)设P点的坐标为(x，y)，由已知条件得|y|＝3，|x|＝4，所以y＝±3，x＝±4，所以P点的坐标为(4，3)或(-4，3)或(4，-3)或(-4，-3)．【总结升华】抓住平面直角坐标系中点的特征和点的特征的意义是解决此类问题的关键．【高清课堂：平面直角坐标系单元复习 2（4）（5）】举一反三：【变式】已知，点P（-m，m-1），试根据下列条件：（1）若点P在过A（2，-4），且与x轴平行的直线上，则m=，点P的坐标为．（2）若点P在过A（2，-4），且与y轴平行的直线上，则m=，点P的坐标为．【答案】（1）-3，（3,-4）; （2）-2，（2，-3）.3. (德阳市)如图所示，在平面直角坐标系中，有若干个整数点其顺序按图中“→”方向排列，如(1，0)，(2，0)，(2，1)，(3，2)，(3，1)，(3，0)…，根据这个规律探索可得，第100个点的坐标为________．【答案】(14，8)【解析】从特殊情形出发：横坐标为1的整数点有1个，横坐标为2的整数点有2个，横坐标为3的整数点有3个，依次类似，横坐标为n 的整数总共有n 个．故共有1+2+3+4+…+n ＝12n ·(n+1)个，由题意分析推测： 当横坐标为14即n ＝14时，共有12×14×(14+1)＝105； 当横坐标为13即n ＝13时，共有12×13×(13+1)＝91； 故第100个点的横坐标为14，而横坐标为14的点共有14个，按“→”向上方向，故纵坐标13-5＝8．【总结升华】当我们面临的数学问题比较抽象而无法下手时，可以从个别的、特殊的情形入手，通过对特例的分析、思考寻找解题的途径，这种思考问题的方法值得学习和借鉴． 举一反三：【变式】(某某)某校数学课外小组，在坐标纸上为学校的一块空地设计植树方案如下：第k 棵树种植在(,)k k k P x y 处，其中x 1＝1，y 1＝1，当k ≥2时，111215,5512,55k k k k k k x x k k y y --⎧⎛--⎫⎡⎤⎡⎤=+--⎪ ⎪⎢⎥⎢⎥⎪⎣⎦⎣⎦⎝⎭⎨--⎡⎤⎡⎤⎪=+-⎢⎥⎢⎥⎪⎣⎦⎣⎦⎩[a]表示非负实数a 的整数部分，例如[2.6]＝2，[0.2]＝0．按此方案，第2009棵树种植点的坐标为( ).A ．(5，2009)B ．(6，2010)C ．(3，401)D ．(4，402)【答案】D.类型三、坐标方法的简单应用4.如图所示，三角形ABC 三个顶点的坐标分别是A(2，-2)，B(1，2)，C(-2，-1)．求三角形ABC 的面积．【思路点拨】观察三角形ABC 的三边都不与坐标轴平行，此时可构造一个过三角形三个顶点的正方形ADEF ．用正方形ADEF 的面积，减去三角形ABD ，三角形BCE ，三角形ACF 的面积即得三角形ABC 的面积．【答案与解析】解：过点A ，C 分别作平行于y 轴的直线，过点A ，B 分别作平行于x 轴的直线，它们的交点为D ，E ，F ，得到正方形ADEF ，则该正方形的面积为4×4＝16．三角形ABD 、三角形BCE 、三角形ACF 的面积分别是：11422⨯⨯=，133 4.52⨯⨯=，11422⨯⨯=． 所以三角形ABC 的面积为16-2-4.5-2＝7.5．【总结升华】本例通过图形的转化，点的坐标与线段长度的转化解决了求图形面积的问题．点的坐标能体现它到坐标轴的距离，于是将点的坐标转化为点到坐标轴的距离，这种应用十分广泛．【高清课堂：平面直角坐标系单元复习 9】举一反三：【变式】如果点()1,0A -，()3,0B ，点C 在y 轴上，且△ABC 的面积是4，求C 点坐标．【答案】解：△ABC 的底AB 的长为：3(1)4--=，则高为：4224⨯=，即点C 的纵坐标为±2， 又点C 在y 轴上，所以点C 的坐标为（0，﹣2）或（0,2）．5. (某某)如图所示，在直角坐标平面内，线段AB 垂直于y 轴，垂足为B ，且AB ＝2，如果将线段AB 沿y 轴翻折，点A 落在C 处，那么C 的横坐标是_______．【答案】-2.【解析】将线段AB 沿y 轴翻折以后，点A 与点C 关于y 轴对称，则两点的横坐标互为相反数，点A 的横坐标为2，则点C 的横坐标为-2．【总结升华】考查平面直角坐标系内图形与坐标的关系以及轴对称的性质．类型四、综合应用6.（）（1）对数轴上的点P 进行如下操作：先把点P 表示的数乘以13，再把所得数对应的点向右平移1个单位，得到点P 的对应点P '.点A B ，在数轴上，对线段AB 上的每个点进行上述操作后得到线段A B ''，其中点A B ，的对应点分别为A B ''，．如图1，若点A 表示的数是3-，则点A '表示的数是；若点B '表示的数是2，则点B 表示的数是；已知线段AB 上的点E 经过上述操作后得到的对应点E '与点E 重合，则点E 表示的数是；（2）如图2，在平面直角坐标系xOy 中，对正方形ABCD 及其内部的每个点进行如下操作：把每 个点的横、纵坐标都乘以同一种实数a ，将得到的点先向右平移m 个单位，再向上平移n 个单位（00m n >>，），得到正方形A B C D ''''及其内部的点，其中点A B ，的对应点分别为A B ''，.已知正方形ABCD 内部的一个点F 经过上述操作后得到的对应点F '与点F 重合，求点F 的坐标.【思路点拨】（1）根据题目规定，以及数轴上的数向右平移用加计算即可求出点A′，设点B 表示的数为a ，根据题意列出方程求解即可得到点B 表示的数，设点E 表示的数为b ，根据题意列出方程计算即可得解：点A′：－3×13+1=－1+1=0.设点B 表示的数为a ，则13a+1=2，解得a=3. 设点E 表示的数为b ，则13a+1=b ，解得b=32. （2）先根据向上平移横坐标不变，纵坐标加，向右平移横坐标加，纵坐标不变求出平移规律，然后设点F 的坐标为（x ，y ），根据平移规律列出方程组求解即可.【答案与解析】【总结升华】根据题目规定，以及数轴上的数向右平移用加计算即可求出点A′，设点B 表示的数为a ，根据题意列出方程求解即可得到点B 表示的数，设点E 表示的数为b ，根据题意列出方程计算即可得解.举一反三：【变式】 把点P 1(m ，n)向右平移3个单位长度再向下平移2个单位长度到一个位置P 2后坐标为P 2 (a ，b)，则m ，n ，a ，b 之间存在的关系是________________.【答案】3a m =+，2b n =-.。

《平行线与相交线》全章复习与巩固（基础）知识讲解【学习目标】1．熟练掌握对顶角，邻补角及垂线的概念及性质，了解点到直线的距离与两平行线间的距离的概念；2.区别平行线的判定与性质，并能灵活运用；3.了解命题的概念及构成，并能通过证明或举反例判定命题的真假；.【高清课堂：相交线与平行线单元复习403105知识结构】【知识网络】【要点梳理】知识点一、相交线1.对顶角、邻补角两直线相交所成的四个角中存在几种不同关系，它们的概念及性质如下表：图形顶点边的关系大小关系对顶角有公共顶点∠1的两边与∠2的两边互为反向延长线对顶角相等即∠1=∠21 2 ∠1与∠2邻补角有公共顶点∠3与∠4有一条边公共，另一边互为反向延长线.邻补角互补即∠3+∠4=180°要点诠释：⑴对顶角是成对出现的，对顶角是具有特殊位置关系的两个角.对顶角的特征:有公共顶点，角的两边互为反向延长线.⑵如果∠α与∠β是对顶角，那么一定有∠α=∠β；反之如果∠α=∠β，那么∠α与∠β不一定是对顶角.⑶如果∠α与∠β互为邻补角，则一定有∠α+∠β=180°；反之如果∠α+∠β=180°，则∠α与∠β不一定是邻补角.邻补角的特征:有公共顶点，有一条公共边，另一边互为反向延长线．⑶两直线相交形成的四个角中，每一个角的邻补角有两个，而对顶角只有一个.2.垂线及性质、点到直线的距离（1）垂线的定义：当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，其中的一条直线叫做另一条直线的垂线，它们的交点叫做垂足.如图1所示，符号语言记作： AB ⊥CD，垂足为O.要点诠释：要判断两条直线是否垂直，只需看它们相交所成的四个角中，是否有一个角是直角，两条线段垂直，是指这两条线段所在的直线垂直.（2）垂线的性质：垂线性质1：过一点有且只有一条直线与已知直线垂直 (与平行公理相比较记).垂线性质2：连接直线外一点与直线上各点的所有线段中，垂线段最短.简称：垂线段最短.（3）点到直线的距离：直线外一点到这条直线的垂线段的长度，叫做点到直线的距离，如图2：PO⊥AB，点P 到直线AB的距离是垂线段PO的长.要点诠释：垂线段PO是点P到直线AB所有线段中最短的一条.知识点二、平行线1．平行线的判定判定方法1：同位角相等，两直线平行．判定方法2：内错角相等，两直线平行．判定方法3：同旁内角互补，两直线平行．要点诠释：根据平行线的定义和平行公理的推论，平行线的判定方法还有：（1）平行线的定义：在同一平面内，如果两条直线没有交点（不相交），那么两直线平行. （2）如果两条直线都平行于第三条直线，那么这两条直线平行（平行线的传递性）. （3）在同一平面内，垂直于同一直线的两条直线平行.（4）平行公理：经过直线外一点，有且只有一条直线与这条直线平行.2．平行线的性质性质1：两直线平行，同位角相等；性质2：两直线平行，内错角相等；性质3：两直线平行，同旁内角互补.要点诠释：根据平行线的定义和平行公理的推论，平行线的性质还有：（1）若两条直线平行，则这两条直线在同一平面内，且没有公共点．（2）如果一条直线与两条平行线中的一条直线垂直，那么它必与另一条直线垂直．3．两条平行线间的距离如图3，直线AB∥CD，EF⊥AB于E，EF⊥CD于F，则称线段EF的长度为两平行线AB 与CD间的距离.要点诠释：（1）两条平行线之间的距离处处相等.（2）初中阶级学习了三种距离,分别是两点间的距离、点到直线距离、平行线间的距离.这三种距离的共同点在于都是线段的长度,它们的区别是两点间的距离是连接这两点的线段的长度,点到直线距离是直线外一点引已知直线的垂线段的长度, 平行线间的距离是一条直线上的一点到与之平行的另一直线的距离.（3）如何理解“垂线段”与“距离”的关系：垂线段是一个图形，距离是线段的长度，是一个量，它们之间不能等同.知识点三、命题及平移1.命题：判断一件事情的语句，叫做命题．每个命题都由题设、结论两部分组成.题设是已知事项；结论是由已知事项推出的事项.2.平移：在平面内，将一个图形沿某个方向移动一定的距离，图形的这种移动叫做平移．要点诠释：平移的性质：（1）平移后，对应线段平行（或共线）且相等；（2）平移后，对应角相等；（3）平移后，对应点所连线段平行且相等；（4）平移后，新图形与原图形是一对全等图形.【典型例题】类型一、相交线1.如图，直线AB、CD、EF相交于点O，那么互为对顶角（平角除外）的角共有对，它们分别是，共有对邻补角.【思路点拨】根据邻补角定义和对顶角定义，每一个顶点处有四个角，可以组成四对邻补角和两对对顶角，而本题图形中，三个顶点重叠在一起，所以再乘以3即可．【答案】6,∠AOC与∠BOD，∠AOF与∠BOE，∠COF与∠DOE, ∠BOC与∠AOD，∠BOF与∠AOE, ∠DOF与∠COE ,12【解析】找对顶角或邻补角，先从某一个角开始，顺时针或逆时针旋转，这样做，既不漏也不重.【总结升华】两条直线相交得到的四个角中，共有2对对顶角，4对邻补角.举一反三：【变式】如图所示，已知∠AOD=∠BOC，请在图中找出∠BOC的补角,邻补角及对顶角.【答案】解：因为∠BOC＋∠AOC=180º（平角定义）,所以∠AOC是∠BOC的补角.因为∠AOD＋∠BOD=180º（平角定义）,∠AOD=∠BOC（已知）,所以∠BOC＋∠BOD=180º.所以∠BOD是∠BOC的补角．所以∠BOC的补角有两个：∠BOD和∠AOC.而∠BOC的邻补角只有一个∠AOC，且∠B OC没有对顶角.2.已知：如图，直线a、b、c两两相交，且a⊥b，∠1＝2∠3，，求∠4的度数.【答案与解析】解：∵a⊥b,∴∠2＝∠1＝90°.又∵∠1＝2∠3，∴90°＝2∠3，∴∠3＝45°,又∠3与∠4互为邻补角，所以∠3+∠4＝180°即45°+∠4＝180°.所以∠4＝135°.【总结升华】涉及到角的运算时，充分利用已知条件和隐含条件（平角、余角、补角、对顶角等）是解题的关键．类型二、平行线的性质与判定3.如图，已知∠ADE = ∠B，∠1 =∠2，那么CD∥FG吗？并说明理由.【答案与解析】解：平行，理由如下：因为∠ADE=∠B，所以DE∥BC（同位角相等，两直线平行），所以∠1=∠BCD（两直线平行，内错角相等）.又因为∠1=∠2（已知），所以∠BCD=∠2.所以CD∥FG（同位角相等，两直线平行）.【总结升华】反复应用平行线的判定与性质，见到角相等或互补，就应该想到判断直线是否平行，见到直线平行就应先想到角相等或角互补.【高清课堂：相交线与平行线单元复习403105经典例题3】举一反三：【变式】如图，已知∠1+∠2=180°，∠3=∠B，试判断∠AED与∠ACB的大小关系，并说明理由．【答案】∠AED=∠ACB，理由如下：∵∠1＋∠2＝180°，又∠1＋∠4＝180°,∴∠2＝∠4.∴AB∥EF（内错角相等，两直线平行）.∴∠5＝∠3.又∠3=∠B,∴∠5＝∠B.∴DE∥BC（同位角相等，两直线平行）.∴∠AED=∠ACB(两直线平行,同位角相等).类型三、命题及平移4.(某某中考)如图所示，请你填写一个适当的条件：________，使AD∥BC．【思路点拨】欲证AD∥BC，结合图形，故可按同位角相等、内错角相等和同旁内角互补两直线平行来补充条件．【答案】∠FAD＝∠FBC，或∠ADB＝∠CBD，或∠ABC+∠BAD＝180°.【解析】解：本题答案不唯一，如：利用“同位角相等，两直线平行”，可添加条件∠FAD＝∠FBC；利用“内错角相等，两直线平行”，可添加条件∠ADB＝∠CBD；利用“同旁内角互补，两直线平行”，可添加条件∠ABC+∠BAD＝180°．【总结升华】这是一道开放性试题，分清题设和结论：结论： AD∥BC，题设可根据平行线的判定方法，逐一寻找即可.举一反三：【变式】下列命题真命题是( )A．互补的两个角不相等 B．相等的两个角是对顶角C．有公共顶点的两个角是对顶角 D．同角或等角的补角相等【答案】D5.如图(1)，线段AB经过平移有一端点到达点C，画出线段AB平移后的线段CD．【思路点拨】连接AC或BC便得平移的方向和距离．【答案与解析】解：如图(2)，线段CD有两种情况：(1)当点A平移到点C时，则点D在点C的下方，因此下边线段CD即为所求；(2)当点B平移到点C时，则点D在点C的上方，上边线段CD即为所求．【总结升华】平移是由平移的方向和距离决定的．本题中未指明哪一端点(A还是B)移动到点C，故应有两种情况：即点A平移到点C或点B平移到点C．举一反三：【变式】下列说法错误的是（）A．平移不改变图形的形状和大小B．平移中图形上每个点移动的距离可以不同C．经过平移，图形的对应线段、对应角分别相等D．经过平移，图形对应点的连线段相等【答案】B类型四、实际应用6.如图，107国道a上有一个出口M，想在附近公路b旁建一个加油站，欲使通道最短，应沿怎样的线路施工？【答案与解析】解：如图，过点M作MN⊥b，垂足为N，欲使通道最短，应沿线路MN施工.【总结升华】灵活运用垂线段最短的性质是解答此类问题的关键.。

几何综合知识框架几何综合题型一般以基本图形（正方形、特殊平行四边形、等边、等腰、直角三角形等）为载体，考查运用图形变换（平移、旋转、轴对称）分析图形中基本量之间的数量关系的探究过程。

涉及初中数学九大几何模型：1、中点类辅助线2、角平分线、垂直平分线类辅助线3、相似模型4、旋转之手拉手模型5、旋转之对角互补模型6、旋转之半角模型7、旋转之构造等边三角形8、旋转之费马点模型9、最短距离问题解题思路：从复杂的图形中“抽”出简单图形，在简单图形中进行逻辑推导，应用相关几何模型，找到解题思路。

知识梳理中点类辅助线见中点---倍长中线：凡是出现中线或类似中线的线段，都可以考虑倍长中线，倍长中线的目的是可以旋转等长度的线段，从而达到将条件进行转化的目的。

在△ABC中, AD是BC边中线。

方式1：直接倍长，(图1)：延长AD到E，使DE=AD，连接BE例：已知在△ABC中，AD是BC边上的中线，E是AD上一点，且BE=AC，延长BE 交AC于F，求证：AF=EF方式2：间接倍长1)（图2）作CF⊥AD于F，作BE⊥AD的延长线于E, 连接BE2)（图3）延长MD到N，使DN=MD，连接CD例：如图，△ABC中，E、F分别在AB、AC上，DE⊥DF，D是中点，试比较BE+CF 与EF的大小.方式3：平行线间线段有中点如图：AD∥BE，F为DE中点。

可构造8字全等△ADF≌△HEF。

例：如图，在矩形ABCD中，BD=BE，F为DE中点。

试探究AF与CF之间的位置关系。

例：如图，在平行四边形ABCD中，BC=2AB，M为AD中点，CE⊥AB。

求证：∠EMD=3∠MEA。

见多个中点----构造中位线：已知三角形的两边有中点，可以连接这两个中点构造中位线；已知一边中点，可以在另一边上取中点，连接构造中位线；已知一边中点，过中点作平行线可构造相似三角形.例：如图，在四边形ABCD中，AB=CD，E、F分别是BC、AD的中点，BA、CD 的延长线分别交EF的延长线G、H。