简易方程的解法归纳完整版

《简易方程》单元知识梳理一、简易方程（一）简单方程（4个）：x+a=b; x-a=b; ax=b; x÷a=b.解：x+a-a=b-a 解：x-a+a=b+a 解：ax÷a=b÷a 解：x÷a×a=b×a x=b-a x=b+a x=b÷a x=ba （二）稍复杂方程（5个）：1、a-x=b 如：20-x=92、a÷x=b 如：2.1÷x=3 解：a-x+x=b+x 解：a÷x×x=b×xa=b+x a=b×xx+b=a bx=a3、ax+b=c 如：6x+3=9 4x- 2.8=10 3x+12×6=6 解：ax+b-b=c-bax=c-b4、a(x+b)=c 如：7(x+2.8)=35 (x-3)÷2=7.5 解：a(x+b)÷a=c÷a 或解：ax+ab=cx+b=c÷a ax+ab-ab=c-abax=c-ab5、ax±bx=c 如：2x+1.5x=17.5 8x-3x=105 3x+x-6=26解：(a±b)x=c（三）其他方程如： 1.2x÷3= 4.8 (5x-12)×8=24 (100-3x)÷2=8二、列方程解决实际问题-----典型例题解析列方程解决实际问题的步骤：1、找出未知数，用字母x表示；2、找出等量关系，列方程；3、解方程并检验作答。

（一）方程模型---x+a=b; x-a=b; ax=b ; x÷a=b甲数是b，甲数比乙数多（少）a，求乙数？或甲数是b，甲数是乙数的a倍，求乙数?等量关系式：乙数＋a=甲数（乙数－a=甲数）或乙数×a=甲数典型例题：1、一件衣服现价178元钱，比原来降低了121元，这件衣服原价多少钱？2、黄豆长成豆芽后的质量是原来质量的8.5倍，现需要豆芽493千克，需要黄豆多少千克？（二）方程模型----ax＋b=c或ax-b=c甲数是c，甲数比乙数的a倍多（少）b，乙数是多少？（设乙数为x.）等量关系式：乙数×a＋b=甲数或乙数×a－b=甲数典型例题：1、一张桌子售价97元，比一把椅子售价的3倍多4元，一把椅子多少元？2、一只大象的体重是5吨，大象的体重比奶牛的8倍少200千克，奶牛的体重是多少千克？（三）方程模型-----ax+b×c=d已知甲乙两种商品的总价d与甲商品的单价b和数量c，求乙商品的单价或数量。

简单方程的解法在数学中，方程是一种包含未知数的等式，通过找到未知数的值使等式成立，可以解决各种实际问题。

在这篇文章中，我们将探讨简单方程的解法。

1. 一元一次方程一元一次方程是最简单且最常见的一种方程。

它只包含一个未知数，并且未知数的最高次数为一。

一元一次方程的一般形式为: ax + b = 0，其中a和b是已知数，x是未知数。

为了解这种方程，我们需要将未知数单独放在等式的一边，将已知数放在另一边。

通过对等式进行恰当的运算，我们可以得到未知数的值。

例如，考虑方程2x + 3 = 7，我们可以先将常数项3移到等式的另一边，得到2x = 7 - 3 = 4。

然后，我们可以继续将系数2除以2，从而得到x = 4/2 = 2。

因此，方程的解为x = 2。

2. 一元二次方程一元二次方程是一种具有未知数的二次项的方程。

一元二次方程的一般形式为：ax^2 + bx + c = 0，其中a、b、c是已知数，x是未知数。

为了解这种方程，我们可以使用配方法、公式法或因式分解等方法。

配方法是一种通过重新排列方程，使其可以被因式分解的方法。

例如，考虑方程x^2 + 5x + 6 = 0，我们可以将常数项6进行因式分解，得到(x + 2)(x + 3) = 0。

因此，方程的解为x = -2或x = -3。

公式法是一种使用一元二次方程的求根公式来解决方程的方法。

一元二次方程的求根公式为x = (-b ± √(b^2 - 4ac)) / (2a)。

例如，考虑方程x^2 + 5x + 6 = 0，根据公式，我们可以计算出x的值。

通过代入a = 1，b = 5，c = 6，我们得到x = (-5 ± √(5^2 - 4*1*6)) / (2*1)。

化简后，我们得到x = -2或x = -3。

因式分解是一种将二次方程分解为两个一次因式的方法。

例如，考虑方程x^2 + 5x + 6 = 0，我们可以尝试将方程因式分解为(x + m)(x + n) = 0的形式。

简单方程的解法与应用方程是数学中常见的一种表达式，表示了两个等值的关系。

在日常生活和工作中，我们经常会遇到各种各样的问题需要通过方程来求解。

本文将介绍一些简单方程的解法与应用。

一、一元一次方程的解法一元一次方程是最简单的方程形式，它的表达式为ax + b = 0。

其中a和b是已知的实数常量，x是未知数。

解一元一次方程的方法有两种：1. 直接法：通过一些简单的计算，我们可以将方程转化为x的形式，并求得x的值。

例如，对于方程2x + 3 = 0，我们可以先减去常数项3，得到2x = -3，再除以系数2，得到x = -3/2。

所以方程的解为x = -3/2。

2. 消元法：通过变形和移项，我们可以将方程转化为a'x = b'的形式，其中a'和b'是已知的实数常量，x是未知数。

然后我们只需将方程中x的系数除以a'，即可求得x的解。

例如，对于方程3x + 4 = 7，我们可以先减去常数项4，得到3x = 3，再除以系数3，得到x = 1。

所以方程的解为x = 1。

二、一元二次方程的解法一元二次方程是一个次数为2的一元方程，它的表达式为ax^2 + bx + c = 0。

其中a、b和c是已知的实数常量，x是未知数。

解一元二次方程的方法有以下几种：1. 因式分解法：当一元二次方程可以被因式分解为两个一元一次方程的乘积时，我们可以通过设置每个一元一次方程等于0，然后求解得到x的值。

例如，对于方程x^2 + 5x + 6 = 0，我们可以将其分解为(x + 2)(x + 3) = 0，然后设置x + 2 = 0和x + 3 = 0，求解得到x = -2和x = -3。

所以方程的解为x = -2和x = -3。

2. 公式法：根据一元二次方程的公式x = (-b ± √(b^2 - 4ac)) /(2a)，我们可以计算出x的值。

其中±表示两个解，√表示平方根。

简易方程式怎么解
简易方程式是指一般有形式为ax+b=c的简单方程，其中a、b、c都是一般的实数，同时a不能为0，而求解这类方程式的方程有两种，一种是因式分解法，另一种是移项法。

首先介绍的是因式分解法，因式分解法主要是将ax+b认为是一个分式，于是将这个式子变形成另一种形式，即ax+b=ac/c。

由于ac/c等于a，所以得出结果就为x=c/a-b/a，这即是求助的解法，而在求解时只要有c/a的结果即可，其中a是可以认为是1的，即可以省略不计。

除了因式分解法，另一种常用的方法即为移项法，而其基本思想即是把ax+b上面的a乘以-1，使其变为-(ax+b)，这样整个等式就变成了c-(ax+b)，此时两边同时加上ax+b，即可变成ax=c，由此得出求解结果为x=c/a。

在求解简易方程式时，因式分解法和移项法均可以很好的利用，使用其中任一一种方法都可轻易的求得x的值，同时移项法通过把因子a移到另一边去求得了更优秀的形式，而且a也可以从等式中剔除掉从而简化求解步骤。

1、解形如X±a=b的方程X+a=b X-a=b 解：X+a-a=b-a 解：X-a+a=b+a X=b-a X=b+a2、解形如a-X=b的方程※a-X=b解：a-x+x=b+xa=b+xa-b=b-b+xx=a-b3、解形如ax=b的方程aX=b解; ax÷a=b÷aX=b÷a4、解形如a÷x=b的方程※a÷X=b解：a÷X×X=b×Xa=b×Xa÷b=b÷b×XX=a÷b5、解形如x÷a=b的方程※X÷a=b解：X÷a×a=b×aX=b×a 6、解形如ax±b=c(a≠0)的方程aX-b=c(a≠0)把“ax”看作一个整体解：ax-b+b=c+bax=c+bax÷a=(c+b) ÷ax=(c+b) ÷aaX+b=c(a≠0)解：ax+b-b=c-b 把“ax”看作一个整体方程的两边同时减去b ax=c-bax÷a=(c-b)÷ax=(c-b)÷a7、解形如ax±ab=c(a≠0)的方程可以转化为：a(x±b)=c 再解8、解形如a(x+b)=c (a≠0)的方程把“x+b”看作一个整体,方程的两边同时除以a书写格式例如 80-X=60解：80-X+X=60+X 检验：x=20代入原方程80=60+X 方程左边=80-X80-60=60-60+X =80-20X=20 =60=方程的右边所以x=20是方程的解定律、公式1、加法交换律：a+b=b+a加法结合律:(a+b)+c=a+(b+c)2、乘法交换律：a ×b=b ×a乘法结合律：(a ×b)×c=a ×(b ×c) 乘法分配律：(a+b)×c=a ×c+b ×c或 (a-b)×c=a ×c-b ×c3、减法性质：a-b-c=a-(b+c)a-b-c=a-c-b4、除法性质：a ÷b ÷c=a ÷(b ×c) a ÷b ÷c=a ÷c ÷b5、去括号： a+(b-c)=a+b-c a-(b-c)=a-b+ca ÷b ×c= a ÷(b ÷c)6、长方形：a长方形周长=(长+宽)×2 字母公式：C=(a+b)×2 长方形面积=长×宽 字母公式：S=ab 7、正方形：正方形周长=边长×4 字母公式：C=4a 正方形面积=S=a ×a 8、平行四边形字母公式：S=ah 9、三角形a三角形的面积=底×高÷2 字母公式：S=ah ÷2 三角形的 底=面积×2÷高；三角形的 高=面积×2÷底） 10、梯形 上底a下底b梯形的面积=（上底+下底）×高÷2 母字公式： S=（a+b）h÷2 上底=面积×2÷高－下底下底=面积×2÷高-上底高=面积×2÷（上底+下底）。

小学解方程10种方法汇总一、未知数加减乘除1.形如x+a=b或x-a=b的方程。

(遇加同减，遇减同加)例1 x+7=19 遇加同减解：x+7-7=19-7 两边同时减去7X=12例2 x－6=19 遇减同加解：x-6+6=19+6 两边同时加上6x=252.利用等式解形如ax=b或x÷a=b(a不等于0)的方程。

（遇乘同除，遇除同乘）例1 7x=63 遇乘同除解：7x÷7=63÷7两边同时除以7x=9例2 x ÷7=9 遇除同乘解：x÷7×7=9×7两边同时乘以7x=633.利用等式解形如ax+b=c、ax-b=c或x÷a+b=c、x÷a-b=c(a不等于0)的方程。

（混合运算，先加减再乘除：能计算的要先计算）例1 2x+5=29 有乘法和加法，先算加法，遇加同减解：2x+5-5=29-5 两边同时减去52x=24 遇乘同除2x÷2=24÷2两边同时除以2x=12例2 5x-6=24 有乘法和减法，先算减法，遇减同加解： 5x-6+6=24+6 两边同时加上65x=30 遇乘同除5x÷5=30÷5两边同时除以5x=6例3 x÷7+3=10 有除法和加法，先算加法，遇加同减解：x÷7+3-3=10-3 两边同时减去3x÷7=7 遇除同乘x÷7×7=7×7两边同时乘以7x=49例4 x÷10-6=9 有除法和减法，先算减法，遇减同加x÷10-6+6=9+6 两边同时加上6x÷10=15遇除同乘x÷10×10=15×10两边同时乘以10x=150二、未知数被加上或被减去；4.未知数被加上a+x=b，a+bx=c（解法同上）5.形如b-x=c、b-ax=c的方程。

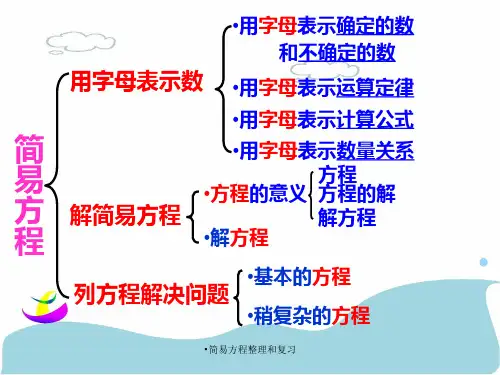
第五单元《简易方程》知识点归纳一、用字母表示数1、在含有字母的式子里，字母之间的乘号可以记作“·”，也可以省略不写。

例如：2×a=2a ；a×b=ab ；注意：①省略“×”时，要把数字写在字母的前面，例如：2×a=2a，不是：a2 ②加号、减号、除号以及数字与数字之间的乘号不能省略。

例如：a+b≠ab ；2×3=6≠23；2a×5=10≠25a 注意：1×a=a，这里的“1”我们省略不写2、a×a可以写作a·a或a2，a2读作a的平方；2a表示a+a或2×a3、面积通常用字母（S）表示，周长通常用C表示长方形面积=长×宽；=a×b用字母表示公式：S长长方形周长=（长+宽）×2用字母表示公式：C=（ a + b ）×2 = 2（a+b）长正方形面积=边长×边长；=a×a=a2，用字母表示公式：S正正方形周长=边长×4用字母表示公式：C=4a；正4、用字母表运算定律。

加法交换律：a+b=b+a加法结合律：a+b+c=a+(b+c)乘法交换律：ab＝ba乘法结合律：a×b×c＝a×(b×c)乘法分配律：(a+b)×c＝ac + bc或(a-b)×c = ac-bc5、利用乘法的分配律化简含字母的式子：ac+bc=(a+b)×c或ac - bc＝(a-b)×c 例如：7a+8a=15a ；8y-y=7y ；2m+3+6m=8m+6 ；6a-a+4=5a+4二、简易方程1、方程：含有未知数的等式称为方程（★方程必须满足的条件：必须既有等式也有未知数，两者缺一不可）。

方程一定是等式，但等式不一定是方程。

例如：2x-3=2，既含有未知数，又是等式，属于方程。

数学简单方程的解法数学中的方程是一种数学关系，其中包含一个或多个未知数，我们需要找到使方程成立的未知数的值。

在数学中，方程是一种重要的工具，用于解决各种实际问题和理论推导。

本文将介绍一些常见的数学简单方程的解法。

一、一元一次方程的解法一元一次方程是最简单的方程形式，它只包含一个未知数和一个一次项。

假设我们要解方程"ax + b = 0"，其中"a"和"b"为已知常数，"x"为未知数。

我们可以按照以下步骤解决该方程：1. 将方程转化为标准形式："ax = -b"。

2. 根据方程中的未知数系数"a"，可以将方程表示为"x = -b/a"。

3. 利用该公式计算出"x"的值。

二、一元二次方程的解法一元二次方程是指包含一个未知数和一个二次项的方程形式。

常见的一元二次方程形式为"ax^2 + bx + c = 0"，其中"a"、"b"和"c"为已知常数，"x"为未知数。

我们可以按照以下步骤解决该方程：1. 利用配方法，将方程转化为标准形式："ax^2 + bx + c = 0"。

2. 对于一元二次方程，我们可以使用求根公式来计算"x"的值。

求根公式为"x = (-b ±√(b^2 - 4ac)) / (2a)"。

3. 将已知的"a"、"b"和"c"的值代入求根公式，计算出"x"的值。

三、一元高次方程的解法一元高次方程是指包含一个未知数和高于二次项的项的方程形式。

对于一元高次方程的解法可以有多种方法，如因式分解法、配方法、Vieta定理等。

解：设梨树有X棵。
x+30=15
（2）桔树有150棵，是梨树的3倍，0梨树有几棵？
解：设梨树有X棵。
3X=15
（3）桔树有150棵，比梨树的3倍还0多30棵，梨树有几棵？
解：设梨树有X棵。
3X+30=1
（4）果园运来25捆桔树和梨树，共15500棵，已知每捆桔
树4棵，每捆梨树有几棵？ 解：设梨树有X棵。
（×） （×）
（√ ） （ ×）
1. a2表示2个a相加.( ) 2. b×4=4b. ( ) 3. 当a=5时，a2 +3 =13( ) 4. 当b=1时，2×b=2( )
•简易方程整理和复习
复习：小轿车的速度是a千米／小时，它从广州开往惠州，行了1.5小时后距离 惠州还有32千米。 （1）1.5a表示（ 1.5小时行的路程 ）；广州距离惠州有（ １.５a+３２ ）千米。
②当字母与字母相乘时，省略乘号，用点表示或直接去掉乘号， 如：a×b写成a·b或ab；（通常按字母的先后顺序写）
③字母与1相乘省略1不写，只写字母本身，如：1×a写成a。
④两个一样的字母相乘就写一个字母，再在字母的右上角写上 2，如：a×a通常写成a·a或a2，读作：a的平方。
•简易方程整理和复习
用含有字母的式子表示数、数量关系、公式和定律等。
25×4+25X=15
（5）桔树和梨树共有150棵，桔树棵0数是梨树的2倍，
桔树和梨树各有几棵？ 解：设梨树有X棵，那么桔树有2X棵。
•简易方程整理和复习
2X+X= 150
有两个书架，第一个书架书的本数是第二个的1.5倍。 如果从第一个书架取出50本放入第二个中，则两个 书架的数就一样多。原来两个书架各有几本书？

人教版小学五年级数学上册第五单元《简易方程》知识点梳理人教版小学五年级数学上册第五单元《简易方程》知识点梳理一、用字母表示数 1、乘法的简写字母和字母、数字和字母相乘时，“?”可以写成“?”或者直接忽略不写。

数字和字母相乘忽略乘号不写时，一般把数字写在字母前面。

【例1】用字母表示出边长为a 的正方形的面积和周长。

解：2aa a =?=面积，a a 44=?=周长2、含字母的式子的运算（1）当两个式子带的字母不完全相同时，不能直接相加减。

（2）当两个式子含有相同的字母时，可以用乘法分配律进行合并。

【例2】计算b a a 554++解：b a b a b a a 595)54(554+=+?+=++二、简易方程 1、判断方程含有未知数的等式叫做方程。

【例3】下面属于方程的是（）A.12+x B.1064=+ C.013>-x D.84=a 解析： A 选项没有等号，不是等式，所以不属于方程；B 选项不含未知数，所以不属于方程；C 选项是大于号，不是等号，所以不属于方程；D 选项有等号，也含有未知数a ，所以属于方程。

所以这题的答案是D 。

2、等式的性质（1）等式两边加上或者减去同一个数，左右两边仍然相等。

（2）等式两边乘以同一个数，或者除以同一个不为0的数，左右两边仍然相等。

【例4】如果b a =，根据等式的性质填空。

)(2+=+b a8)(-=-b ab a ?=)(35)(÷=÷b a解：22+=+b a ； 88-=-b a ； b a ?=33；55÷=÷b a 。

3、解方程的书写规范先写“解”，“=”号要对齐，解出来的未知数写在“=”号左边。

4、解方程的方法逆运算：加法用减法抵消、减法用加法抵消、乘法用除法抵消、除法用乘法抵消。

（1）一步方程用逆运算去掉未知数以外的部分。

【当未知数前面是减号或除以号时，两边先要同时加上或者乘以未知数，计算结果左右两边互换后再继续计算】（2）两步以上的方程①方程中没有括号时，先把能计算的先计算出来后，先逆运算加减法，再逆运算乘除法，最后按一步方程的方法解方程。

初中简易方程知识点总结一、方程的基本概念1. 方程方程是指含有未知数和常数之间的相等关系的式子。

一般形式为：a₁x + a₂y +… + aₙz = b其中，a₁，a₂，…，aₙ为系数；b为已知数；x，y，z为未知数；a₁x + a₂y +… + aₙz称为方程的左式；b称为方程的右式。

2. 未知数方程中并不是所有的字母都代表未知数。

未知数是指在方程中所要求解的数。

在方程a +b = 10中，a和b为未知数。

3. 解解是指使方程成立的数或者数的集合。

对于方程a + b = 10，当a = 3，b = 7时，方程成立，此时a=3，b=7就是方程的解。

二、方程的解法1. 移项法移项法是简单方程解法的一个基本方法。

其基本思想是为了使方程两边相等，当方程左边有负数时，把它移至右边转化为正数；当方程右边有负数时，把它移至左边转化为正数。

举例：2x + 5 = 10移项得：2x = 10 - 52x = 5x = 5 / 2x = 2.52. 相消法相消法是简单方程解法的常用方法。

当方程中存在相同的项，且这些相同项可以相互抵消时，可以利用相消法来求解方程。

举例：3x + 2x - 5 = 12合并同类项得：5x - 5 = 12移项得：5x = 12 + 55x = 17x = 17 / 5x = 3.43. 同除法同除法是通过将等式的两边同时除以相同的非零数来消去方程中的分母。

举例：3x / 2 = 6同除得：3x = 6 * 23x = 12x = 12 / 3x = 44. 合并同类项法合并同类项法是在一个等式中将相同的变量或者常数合并在一起，从而简化方程，找到其解。

举例：2x + 3x - 5 = 10合并同类项得：5x - 5 = 10移项得：5x = 10 + 55x = 15x = 15 / 5x = 35. 因式分解法因式分解法是将一个多项式拆解成若干个因式的乘积的方法。

举例：2x(x + 3) = 20因式分解得：2x² + 6x - 20 = 0求根得：x = -5 或 x = 26. 代数法代数法是通过代数运算来求解方程的一种方法。

简单的数学方程式解答数学方程式在我们的日常生活中起着重要的作用，它们用于解决各种问题，并在科学、工程、经济等领域发挥着关键作用。

通过解答数学方程式，我们可以找到未知的变量值，从而使问题得以解决。

在本文中，我们将重点讨论一些简单的数学方程式及其解答方法。

第一类方程式：线性方程式线性方程式是最简单的方程式之一，形式为ax + b = 0，其中a和b是已知常数，x是未知数。

要解答线性方程式，我们可以使用以下步骤：步骤一：将方程式转化为标准形式，即将常数项移到等号的另一侧，得到ax = -b。

步骤二：将方程式两边都除以a，得到x = -b/a，这就是线性方程式的解。

举例来说，考虑方程式2x + 3 = 0，我们可以按照上述步骤进行解答。

首先将常数项移动，变为2x = -3，然后除以2，得到x = -3/2。

因此，方程式2x + 3 = 0的解为x = -3/2。

第二类方程式：二次方程式二次方程式是一种形式为ax^2 + bx + c = 0的方程式，其中a、b、c是已知常数，x是未知数。

要解答二次方程式，我们可以使用以下步骤：步骤一：使用求根公式，即x = (-b ± √(b^2 - 4ac))/(2a)。

步骤二：计算方程式右侧的值，并求出平方根。

举例来说，考虑方程式x^2 + 3x - 4 = 0，我们可以按照上述步骤进行解答。

首先计算b^2 - 4ac，即3^2 - 4(1)(-4)，得到25。

然后，我们可以求出平方根，得到5。

将这些值代入求根公式中，我们可以计算出x的值。

因此，方程式x^2 + 3x - 4 = 0的解为x = (-3 ± 5)/(2*1)，即x = 1或x = -4。

第三类方程式：一次方程组一次方程组是由多个线性方程式组成的方程组，形式为：a1x + b1y + c1 = 0a2x + b2y + c2 = 0要解答一次方程组，我们可以使用以下步骤：步骤一：通过消元法或代入法，将方程组化简为含有一个未知数的方程式。

掌握小学简单代数方程的解法代数方程是数学中常见的问题类型，学习和掌握解决代数方程的方法对于小学生来说非常重要。

下面将介绍几种常见的小学简单代数方程的解法。

1. 一元一次方程一元一次方程是指只含有一个未知数且最高次数为1的方程。

例如：2x + 3 = 9。

解一元一次方程的基本步骤如下：（1）将方程中的常数项移到等号的另一边，得到2x = 9 - 3，即2x = 6。

（2）如果方程中未知数的系数不为1，则将方程两边同时除以该系数，得到x = 6 ÷ 2，即x = 3。

因此，方程的解为x = 3。

2. 一元二次方程一元二次方程是指含有一个未知数且最高次数为2的方程。

例如：x^2 + 5x + 6 = 0。

解一元二次方程的一种方法是利用因式分解法，步骤如下：（1）将方程进行因式分解，得到(x + 2)(x + 3) = 0。

（2）令每个因式分别等于0，即x + 2 = 0和x + 3 = 0。

（3）解得x = -2和x = -3。

因此，方程的解为x = -2和x = -3。

3. 一元一次方程组一元一次方程组是指包含多个一元一次方程的方程组。

例如：2x + y = 53x + 4y = 14解一元一次方程组的方法有代入法、消元法等。

以代入法为例，步骤如下：（1）选择其中一个方程，将其中一个变量表示成另一个变量的函数，如将第一个方程中的x表示成y的函数：x = 5 - y。

（2）将得到的表达式代入到另一个方程中，消去变量得到新的方程：3(5 - y) + 4y = 14。

（3）将方程进行化简，解得y = 2。

（4）将y的解代入之前的表达式，解得x = 3。

因此，方程组的解为x = 3，y = 2。

4. 一元二次方程组一元二次方程组是指包含多个一元二次方程的方程组。

例如：x^2 + y^2 = 25x + y = 7解一元二次方程组的方法有代入法、消元法等。

以代入法为例，步骤如下：（1）选择其中一个方程，将其中一个变量表示成另一个变量的函数，如将第二个方程中的x表示成y的函数：x = 7 - y。

简单的数学方程与解方程的方法数学方程是数学研究中的重要内容之一，它们帮助我们解决各种实际问题，同时也培养了我们的逻辑思维能力。

本文将介绍一些常见的简单数学方程，并给出解方程的方法。

一、一元一次方程一元一次方程是最简单的方程形式，其一般形式为：ax + b = 0，其中a和b是已知数，x是未知数。

解方程的方法：1. 移项法：将方程的各项移至不同的一边，使得方程化简为ax = -b 的形式。

然后，通过除以a得到x = -b/a的解。

2. 等式法：利用等式性质，将方程两边进行等式变形，使得方程化简为x = -b/a的形式。

这样，我们可以直接得到方程的解。

例如，对于方程2x + 3 = 1，我们可以通过移项法将其化简为2x = -2，再除以2得到x = -1的解。

二、一元二次方程一元二次方程是形如ax^2 + bx + c = 0的方程，其中a、b、c为已知数，x为未知数。

解方程的方法：1. 因式分解法：将方程的左边进行因式分解，使得方程化简为(ax + m)(nx + n) = 0的形式。

然后，利用“因式乘积为零时，其中一个因式等于零”的原理，得到方程的解。

2. 公式法：根据一元二次方程的求根公式x = (-b ± √(b^2 - 4ac))/(2a)，其中b^2 - 4ac称为判别式。

当判别式大于零时，方程有两个实数根；当判别式等于零时，方程有一个实数根；当判别式小于零时，方程没有实数根。

例如，对于方程x^2 - 4x + 4 = 0，我们可以通过公式法得到其解为x = 2。

三、一元高次方程除了一元一次方程和一元二次方程，还存在一元高次方程，例如三次方程、四次方程等。

解高次方程的方法多种多样，常见的有：1. 因式分解法：对于具有可分解因式的高次方程，我们可以将其因式分解后得到方程的解。

2. 代数方法：利用代数运算的性质，通过变形、降次等方式化简方程，达到求解的目的。

3. 数值逼近法：通过构造递推关系或使用计算机等工具，逐步逼近方程的解。

边的“x －0.36 x”可以运用乘法分配律进行计算得到 0.64 x，再利用等式的基本性 质，求出方程的解。第（3）题，等号的左右两边同时加上“2 x”，把方程转化成
4
“1.7 + 2 x＝3.5”，再求出方程的解。
温馨提醒：解方程时每一步都是等式，而不是递等式，书写时要注意等号对齐。
解题过程：
x = 1.4 代入方程 2 ×（x - 2.6）= 8，等号的左边 = 2×（1.4 - 2.6），这是小学阶段无法 计算出来的算式，但可以判断出它与右边不相等。因此，x =1.4 不是原方程的解。 仔细观察解方程的过程，发现根据“x - 2.6 = 4”得到“x = 1.4”是错误的，正确的 答案应该是 6.6。
（3）3.5－2 x = 1.7 3.5 - 2 x + 2 x = 1.7 + 2 x
1.7 + 2 x = 3.5 2 x = 1.8 x = 0.9
2 检验法
检验法是指把求得的未知数 x 的值（方程的解）代入原方程进行检验，判断等号 的左边与右边是否相等，再次确认结果的准确性。这是因为解方程与递等式计算有 很大的不同，且步骤较多、书写麻烦，对刚接触方程知识的小朋友来说还有待熟 练，如果省略了一些解题的关键步骤，凭借经验来解题，错误率会非常高。因此， 可以用检验法来判断是否得到了正确的解。
3 设大数法
在列方程解决问题的过程中，出现两个及两个以上的未知数时，我们可以设较 大数为 x。这里的“大数”可以理解得宽泛一些。如“鸡兔同笼”问题中，鸡的脚 数比兔的少，我们可以把兔子看作“大数”，设兔子的只数为 x；再如三轮车与自行 车相比，我们就可以把三轮车看作“大数”，等等。
例 3. 一群小朋友每人骑着一辆二轮或三轮的车子在公园玩， 小明发现共有 7 名小朋友及 19 个车轮子。这群小朋友所骑的车子 中有多少辆三轮车？

工作总量(c)、工作时间(t)、工作 效率(a)的数量关系：
c=at a=c÷t t=c÷a
a+b=b+a (a+b)+c=a+(b+c)
ab=ba
(ab)c=a(bc)
(a+b) c=ac+bc
判断题：
1、因为22=2×2，所以a2=2a（× ）
2、b÷2可以写成2b。
（× ）
3、x÷2=x2
4、a×5=a5
2.一个长方形的长是48分米，宽是b分米，它的周长是（96+）2b分米。
C ＝ 2(a+b ) ＝2(48+b) ＝96+2b
3.小英重n千克，比小华轻3千克，小华体重是（ 3+）n千克。
巩固练习---在括号里填上含有字母的式子。
4.汽车平均每小时行m千米，6小时能行（6m）千米，行450千米
要（ 450÷）m小时。
复习三：果园里一共种了340棵桃树和杏树，其
中桃树的棵数比杏数的3倍多20棵。两种树各种
了多少棵？
X
杏树的棵数： X
X
X 多20 340
桃树的棵数：
3X+2 X+3X+20=340
0
4X+20-20=340-20X=80
3X+20=3×80+20
解：设杏树有X棵。那 么桃树有3X+20棵
被减数 =___________________
一个因数 =___________________
除数
=___________________
被除数 =___________________
列方程解应用题

小学数学知识归纳简单方程的解法和应用数学是一门让人们又爱又恨的学科，对于小学生来说，学习数学是必不可少的。

在小学数学的学习过程中，简单方程的解法和应用是一个重要的内容。

本文将对小学数学中的简单方程解法和应用进行归纳总结。

一、方程的基本概念在开始讨论方程的解法之前，我们先来了解一些方程的基本概念。

方程是表示两个数或量之间相等关系的式子，由等号链接，例如：2+3=5就是一个简单的方程。

方程中的未知数是需要求解出来的数或量。

解方程就是要找到未知数的值，使得方程两端相等。

二、一元一次方程的解法1. 移项法一元一次方程的一种常见解法是移项法。

移项法的基本思想是将含有未知数的项移到方程的同一侧，将常数项移到方程的另一侧，最终求得未知数的值。

例如，对于方程2x+3=9，我们可以通过移项得到2x=9-3，再进行计算得到x=6/2，即x=3。

2. 消元法另一种解一元一次方程的方法是消元法。

消元法的基本思想是通过合并同类项，使得方程中只剩下一个未知数的项。

例如，对于方程3x+2=5x-1，我们可以通过合并同类项得到3x-5x=-1-2，再进行计算得到-2x=-3，即x=3/2。

三、方程的应用方程作为数学的一种工具，在日常生活中有着广泛的应用。

下面我们来看一些常见的方程应用实例。

1. 计算问题方程可以用来解决计算问题，例如：问题1：一个数加上4等于12，求这个数是多少？解法：设这个数为x，则可以列出方程x+4=12，根据移项法，我们可以得到x=12-4，即x=8，所以这个数是8。

2. 推理问题方程也可以用于推理问题，例如：问题2：两个数之和是8，其中一个数是另一个数的3倍，求这两个数分别是多少？解法：设其中一个数为x，则另一个数为3x。

根据题目条件，可以列出方程x+3x=8，根据合并同类项和移项法，我们可以得到4x=8，再进行计算得到x=2，所以其中一个数是2，另一个数是3×2=6。

3. 长方形问题方程还可以用于解决长方形问题，例如：问题3：一个长方形的长是宽的两倍，周长为18米，求长和宽各是多少米？解法：设长方形的长为x，宽为y，则根据题目条件可以列出方程2x+y=18。