对数型复合函数的单调区间选择题(3)

1，函数()22log 22+-=x ax y 的定义域为Q .(1)上是增函数，求实数a 的取值范围；(2)若PQ ϕ≠，求实数a 的取值范围；(3)若关于x 的方程()222log 22=+-x ax 在区间内有解，求实数a 的取值范围.答案：(1)()()4,02,a ∈-⋃+∞； (2)()+∞-∈,4a ； 解答：(1)设222+-=x ax t ，()t t f 2log =①0>a 时，由可得，2≥a ； ②0<a 时，由可得，04<<-a ； ()()+∞⋃-∈∴,20,4a ；(2)若φ=⋂Q P ，则在内，至少x 有一个使0222>+-x ax 成立，内，至少x 有一个使 ，所以()+∞-∈,4a ；(3)若关于x 的方程()222log 22=+-x ax 在区间则0222=--x ax 在区间知2．若b x x x f +-=2)(，且)10(2)(log ,)(log 22≠>==a a a f b a f 且， (1)求)(log 2x f 的最小值及相应 x 的值；(2)若)1()(log )1()(log 22f x f f x f <>且，求x 的取值范围． 答案：(1) )(log 2x f 有最小值(2)0<x<1.解答： (1)()22222 2(1)),2(f x x x b f log a log a log a b b log a a =+∴=-+=∴==-∴,,， 又()()()22224,42, 2log f a f a a a b b f x x x ==∴+=-∴=∴=+,－,，∴222log 0log 1024x x x x <>⎧⎨<-+<⎩或 ， ∴01212x x x <<>⎧⎨-<<⎩或 ， ∴ 0＜x ＜1. 3．已知函数)1,0)(3(log )(≠>-=a a ax x f a . (1)求函数)(x f 的定义域；(2)若函数)(x f 在[2,6]，求实数a 的值. 答案：解答：又⎩⎨⎧>-<<06310a a ，则4. (1)求m 的值；(2)判断)(x f 在),1(+∞上的单调性，并根据定义证明. 答案：(1)1m =-；(2)当01a <<时， ()f x 在(1,)+∞上单调增； 当1a >时， ()f x 在(1,)+∞上单调减. 解答：(1)由已知条件得()()0f x f x +-=，，21m ∴=，即1m =±， 当1m =时，无意义，故1m =舍去， (2)由(1) 1212121221(1)(1)2()0x x x x x x x x x x -+--+--=-<，且121210x x x x -+->， 121210x x x x +-->，当01a <<时，12()()0f x f x ->，由函数单调性定义知()f x 在(1,)+∞上单调增当1a >时，12()()0f x f x -<，由函数单调性定义知()f x 在(1,)+∞上单调减. 5其中01a <<. (1)(2). 答案：(1)见解答； (2) 解答：(1)12()()g x g x ∴< 又1201()()a f x f x <<∴>分)log (1a -101a a a x-<<< 从而 ， x ∴的取值范围是(,)1a a a-. 6．已知函数）m x x x f --++=|2||1(|log )(2．(1)当5=m 时，求函数)(x f 的定义域；(2)若关于x 的不等式1)(≥x f 的解集是R ，求m 的取值范围． 答案：(1)函数)(x f 的定义域为),3()2,(+∞--∞ ； (2)m 的取值范围是]1,(-∞． 解答：(1)由题设知：5|2||1|>-++x x ， 不等式的解集是以下三个不等式组解集的并集：⎩⎨⎧>-++≥5212x x x ，或⎩⎨⎧>+-+<≤52121x x x ，或⎩⎨⎧>+---<5211x x x ， 解得函数)(x f 的定义域为),3()2,(+∞--∞ ； (2)不等式1)(≥x f 即2|2||1|+>-++m x x ，∵R ∈x 时，恒有3|)2()1(||2||1|=--+≥-++x x x x ， 不等式2|2||1|+≥-++m x x 解集是R ， ∴32≤+m ，m 的取值范围是]1,(-∞．7．已知函数()log (1)log (1)a a f x x x =+--,0>a 且1≠a . (1)求()f x 的定义域；(2)判断()f x 的奇偶性并予以证明；(3)当1a >时，求使()0f x >的x 的取值范围. 答案：(1) (2)略；(3) 解答：(1)解: ∵()log (1)log (1)a a f x x x =+--,∴10,10.x x +>⎧⎨->⎩解得11x -<<.(2)由(1)知()f x 的定义域为 且()log (1)log (1)a a f x x x -=-+-+ ，[]log (1)log (1)a a x x =-+--()f x =-,故()f x 为奇函数； (3)()()()()()011011a a a f x log x log x log x loga x >∴+-->∴+>-，，，因为当1a >时，y=log a x 在(0,+∞)内是增函数， 所以x+1>1-x ，所以x>0，又()f x 的定义域为，所以01x <<. 所以使()0f x >的x 的取值范围是8.答案：定义域为）+∞-∞,4()1,( ，值域是R ，单调区间是解答：045)(2>+-=x x x μ，解得4>x 或1<x ，∴）+∞-∞∈,4()1,( x . 当）+∞-∞∈,4()1,( x 时，+=+-=R x x }45|{2μμ，∴函数)(x μ的值域是+R .与45)(2+-=x x x μ复合而成，9．解不等式log (25)log (1)a a x x ->-． 答案：当1a >时，原不等式的解集为{}|4x x >； 当01a <<时，原不等式的解集为 解答：当1a >时，原不等式等价于250,10,251,x x x x ->⎧⎪->⎨⎪->-⎩解得4x >．当01a <<时，原不等式等价于250,10,251x x x x ->⎧⎪->⎨⎪-<-⎩，解得综上，当1a >时，原不等式的解集为{}|4x x >； 当01a <<时，原不等式的解集为 10的值域为[]0,1，求b 和c 的值． 答案：22b c =⎧⎨=⎩或22b c =-⎧⎨=⎩解答：因为()f x 的值域为[]0,1，即2210,30,x bx c x bx c ⎧++-≥⎪⎨-+-≥⎪⎩ 21224(1)0,4(3)0,b c b c ⎧∆=--≥⎪⎨∆=--≥⎪⎩当且仅当120,0∆=⎧⎨∆=⎩时， 解方程组可得2,2b c =⎧⎨=⎩或2,2.b c =-⎧⎨=⎩11．设)1,0)(3(log )1(log )(≠>-++=a a x x x f a a ，且2)1(=f ． (1)求a 的值及)(x f 的定义域； (2)求)(x f 在区间. 答案：(1)2a =定义域为(31)-，； (2)2.解答：(1)∵2)1(=f ，∴24log =a ，∴2a =，则由1030x x +>⎧⎨->⎩，得3(1x ∈-，）所以)(x f 的定义域为(31)-，(2))3(log )1(log )(22x x x f -++=]4)1([log 22+--=x ，设2(1)4t x =--+，则2()log f x t =302x ≤≤，∴当1x =时，max 4t =， 而(0)3t =，，∴当0x =时，min 3t =，34t ∴≤≤，22log 3log 2t ∴≤≤所以)(x f 在区间上的最大值为212．已知函数()()()()log 1log 301a f x x x a =-++<<. (1)求函数()f x 的定义域；(2)若函数()f x 的最小值为-4，求实数a 的值.答案：(1){}|31x x -<<；解答：(1)要使函数有意义，则有103130x x x ->⎧⇒-<<⎨+>⎩ 所以函数的定义域为{}|31x x -<<；(2)函数可化为()()()()()22log 13log 23log 14a a a f x x x x x x ⎡⎤=-+=--+=-++⎣⎦，()()2231,0144,01,log 14log 4a a x x a x ⎡⎤-<<∴<-++≤<<∴-++≥⎣⎦，()min log 4a f x =，由，故实数a 的值为13．已知函数)16(log log )(3224x x x f a ⋅⋅=(1)若1=a ，求方程1)(-=x f 的解集。

《对数型复合函数单调性》专题2014年（ ）月（ ）日 班级： 姓名 不经三思不求教，不动笔墨不读书。

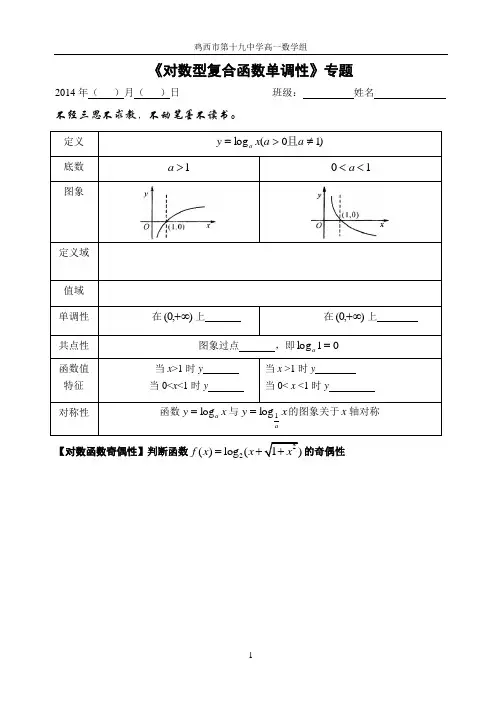
定义)10(log ≠>=a a x y a 且 底数1>a 10<<a图象定义域 值域单调性在),0(+∞上 在),0(+∞上 共点性图象过点 ，即01log =a 函数值特征当x >1时y 当0<x <1时y 当x >1时y 当0< x <1时y 对称性 函数x y a log =与x y a1log =的图象关于x 轴对称【对数函数奇偶性】判断函数22()log (1f x x x =+的奇偶性【探究复合函数单调性】求函数22log y x =的单调区间。

我们发现：22log y x =可以看做：2log y u =且2u x =复合而成，我们把这种函数称为复合函数【规律】当内外函数的单调性相同时，其复合函数是增函数；当内外函数的单调性不相同时，其复合函数是减函数。

“同增异减”例1 ⑴证明函数22()log f x x =在),0(+∞上是增函数⑵函数22()log f x x =在)0,(-∞上是减函数还是增函数？例2 ⑴证明函数)1(log )(22+=x x f 在),0(+∞上是增函数⑵函数)1(log )(22+=x x f 在)0,(-∞上是减函数还是增函数？例3 求函数)32(log 221--=x x y 的单调区间，并用单调定义给予证明【当堂训练】1.求y=3.0log (2x -2x)的单调递减区间2.求函数y=2log (2x -4x)的单调递增区间3.已知y=a log (2-x a )在［0，1］上是x 的减函数，求a 的取值范围.4.已知实数x 满足1213log 2x -≤≤-，求函数22log log 24x x y ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭的值域5.求函数221144log log 5y x x ⎛⎫=-+ ⎪⎝⎭在24x ≤≤时的最大值与最小值。

2021-2022学年吉林省松原市高一上学期第三次质量检测数学试题一、单选题1．设集合{}1,3,5,7A =，{|25}B x x =≤≤，则A B = A ．{1,3} B ．{3,5}C ．{5,7}D ．{1,7}【答案】B【详解】试题分析：集合与集合的公共元素有3，5，故，故选B.【解析】集合的交集运算【名师点睛】集合是每年高考中的必考题,一般以基础题的形式出现,属得分题.解决此类问题一般要把参与运算的集合化为最简形式，再进行运算,如果是不等式的解集、函数的定义域及值域等有关数集之间的运算,常借助数轴求解.2．已知四边形ABCD 的两条对角线分别为AC ，BD ，则“四边形ABCD 为菱形”是“AC BD ⊥”的（ ） A ．充分不必要条件 B ．充要条件C ．必要不充分条件D ．既不充分也不必要条件【答案】A【分析】利用菱形的判定定理和性质定理即可判断二者间的逻辑关系. 【详解】四边形ABCD 的两条对角线分别为AC ，BD ，若四边形ABCD 为菱形，则AC BD ⊥；若AC BD ⊥，则四边形ABCD 不一定为菱形. 则“四边形ABCD 为菱形”是“AC BD ⊥”的充分不必要条件 故选：A3．命题“20,0x x x ∀>-≤”的否定是（ ）A ．20,0x x x ∃>-≤B ．20,0x x x ∃>->C ．20,0x x x ∀>->D ．20,0x x x ∀≤->【答案】B【分析】根据全称量词命题的否定方法写出命题的否定即可. 【详解】因为全称量词命题的否定是存在量词命题， 所以命题“20,0x x x ∀>-≤”的否定为：“20,0x x x ∃>->”. 故选：B.4．若0,0,2a b a b >>+=，则41y a b=+的最小值为（ ） A ．72B ．92C ．5D ．4【答案】B【分析】利用题设中的等式，把y 的表达式转化成()()241a b a b++展开后，利用基本不等式求得y 的最小值．【详解】解：2a b +=， ∴12a b+= ∴41415259()()222222a b b ay a b a b a b +=+=+=+++=（当且仅当2b a =时等号成立） 故选：B ．5．已知点(),8m 在幂函数()()1nf x m x =-的图像上，则m n -=（ ）A ．19B ．18C ．8D ．9【答案】A【解析】根据幂函数的系数为1可求得m 的值，再将点(),8m 的坐标代入函数()f x 的解析式，求出n 的值，进而可求得m n -的值.【详解】由于函数()()1n f x m x =-为幂函数，则11m -=，解得2m =，则()nf x x =，由已知条件可得()228n f ==，得3n =，因此，2139m n --==. 故选：A.6．函数f(x)=23x x +的零点所在的一个区间是 A ．（-2，-1） B ．（-1,0） C ．（0,1） D ．（1,2）【答案】B【详解】试题分析：因为函数f(x)=2x +3x 在其定义域内是递增的，那么根据f(-1)=153022-=-<,f（0）=1+0=1>0,那么函数的零点存在性定理可知，函数的零点的区间为（-1,0），选B ． 【解析】本试题主要考查了函数零点的问题的运用．点评：解决该试题的关键是利用零点存在性定理，根据区间端点值的乘积小于零，得到函数的零点的区间．7．函数212log (56)y x x =-+的单调减区间为（ ）A ．52，⎛⎫+∞ ⎪⎝⎭B ．(3)+∞，C ．52⎛⎫-∞ ⎪⎝⎭，D ．()2-∞，【答案】B【分析】先由解析式求出函数定义域，再由复合函数单调性，即可得出结果. 【详解】由题意，2560x x -+>，解得：3x >或2x <，即函数212log (56)y x x =-+的定义域为：(2)(3)-∞⋃+∞，，， 因为函数212log (56)y x x =-+由12log y t =与256t x x =-+复合而成， 外函数12log y t=显然单调递减，要求212log (56)y x x =-+的单调减区间，只需256t x x =-+单调递增，又256t x x =-+是开口向上，对称轴为52x =的二次函数， 所以256t x x =-+在3()x ∈+∞，上单调递增， 即函数212log (56)y x x =-+的单调减区间为3()x ∈+∞，. 故选：B.【点睛】本题主要考查求对数型复合函数的单调区间，熟记复合函数单调性的判定方法即可，涉及一元二次不等式解法，属于基础题型.8．若()()35,12,1a x x f x ax x ⎧-+≤⎪=⎨>⎪⎩在R 上为减函数，则实数a 的取值范围为（ ） A ．(),0∞- B ．()0,3 C ．(]0,2 D ．()0,2【答案】C【分析】根据()f x 为R 上的减函数列不等式，解不等式求得a 的取值范围. 【详解】()f x 为R 上的减函数， 1x ∴≤时， ()f x 递减，即30a -<，①， 1x >时， ()f x 递减，即0a >，②且()23151aa -⨯+≥ ，③ 联立①②③解得， 02a <≤. 故选：C.【点睛】本小题主要考查根据函数的单调性求参数的取值范围，属于基础题.二、多选题9．若函数1()3(02xf x a a a ⎛⎫=-⋅> ⎪⎝⎭，且1a ≠）是指数函数，则下列说法正确的是（ ）A ．8a =B ．(0)3f =-C ．12f ⎛⎫= ⎪⎝⎭D ．4a =【答案】AC【分析】根据指数函数的定义求出函数解析式，再对选项作出判断．【详解】解：因为函数()f x 是指数函数，所以1312a -=，所以8a =，所以()8xf x =，所以()01f =，12182f ⎛⎫== ⎪⎝⎭B 、D 错误，A ．C 正确． 故选AC【点睛】本题考查指数函数的定义，及函数值的求解，属于基础题． 10．（多选）有下列说法，其中错误的是 A ．终边相同的角的同名三角函数值相等 B ．同名三角函数值相等的角也相等C ．终边不相同，它们的同名三角函数值一定不相等D ．不相等的角，同名三角函数值也不相等 【答案】BCD【分析】根据三角函数的定义即可得出选项． 【详解】对于A ，由诱导公式一可知正确； 对于B ，1sin 30sin1502==，但30150≠，所以B 错误； 对于C ，如60α=，120β=的终边不相同，但3sin 60sin1202==，所以C 错误； 对于D ，由C 中的例子可知D 错误.【点睛】本题考查三角函数的定义，除了掌握住对角的扩充，还要理解三角函数的定义． 11．下列与3cos π-2θ⎛⎫⎪⎝⎭的值相等的是 （ ）A ．()sin πθ-B ．()sin πθ+C ．πcos 2θ⎛⎫- ⎪⎝⎭D ．πcos 2θ⎛⎫+ ⎪⎝⎭【答案】BD【分析】根据诱导公式化简，然后对选项逐一判断即可. 【详解】因为3cos π-sin 2θθ⎛⎫=- ⎪⎝⎭，对于A ，()sin πsin θθ-=； 对于B ，()sin πsin θθ+=-；对于C ，πcos sin 2θθ⎛⎫-= ⎪⎝⎭；对于D ，πcos sin 2θθ⎛⎫+=- ⎪⎝⎭故选:BD.12．已知函数()21([2,2])f x x x =-+∈-，2()2([0,3])g x x x x =-∈，则下列结论正确的是（ ） A ．[2,2]x ∀∈-，()f x a >恒成立，则a 的取值范围是(,3)-∞- B ．[2,2]x ∃∈-，()f x a >，则a 的取值范围是(,3)-∞- C ．[0,3]x ∃∈，()g x a =，则a 的取值范围是[1,3]- D ．[2,2]x ∀∈-，[0,3]t ∃∈，()()f x g t = 【答案】AC【分析】利用函数的单调性讨论最值，再根据恒成立问题或能成立求解即可. 【详解】对于A ，因为()21([2,2])f x x x =-+∈-单调递减，所以min ()3f x =-， 又因为()f x a >恒成立，则a 的取值范围是(,3)-∞-，故A 正确； 对于B ，因为()21([2,2])f x x x =-+∈-单调递减，所以max ()5f x =， 又[2,2]x ∃∈-，()f x a >，则a 的取值范围是(,5)-∞，故B 错误； 对于C ，2()2([0,3])g x x x x =-∈在[]0,1单调递减，(]1,3单调递增， 所以min max ()(1)1,()(3)3,g x g g x g ==-== 所以()[1,3]g x ∈-，因为[0,3]x ∃∈，()g x a =，所以a 的取值范围是[1,3]-，故C 正确； 对于D ，由上述过程可知[]()3,5f x ∈-，()[1,3]g x ∈-， 则不能保证[2,2]x ∀∈-，[0,3]t ∃∈，()()f x g t =，例如：当2x =-时，不存在[0,3]t ∈，()()f x g t =，故D 错误. 故选:AC.三、填空题133⨯=__________.【答案】8【分析】由已知代数式有意义确定x 的范围，结合根式的运算性质化简目标式求其值.310x -≥且30x -≤，故133x ≤≤，()3313331338x x x x ⨯=-+-=-+-=，故答案为：8.14．函数()()log 21(0a f x x a =-+>且1)a ≠的图象恒过的定点是_____________. 【答案】(3,1)【分析】根据对数的运算性质进行求解即可. 【详解】因为()()3log 3211a f =-+=， 所以该函数的图象恒过的定点是(3,1)， 故答案为：(3,1) 15．已知弧度数为3π的圆心角所对的弦长为2，则这个圆心角所对的弧长是__________. 【答案】23π 【分析】设圆的半径为r ，根据圆心角与弦长、半径关系求r ，再由弧长公式求圆心角所对的弧长. 【详解】若圆的半径为r ，则11sin 62r π==，可得2r =， ∴圆心角所对的弧长2233l r ππθ==⨯=. 故答案为：23π 16．已知函数()22log 1a a f x x x x =-+-在31,2⎛⎫⎪⎝⎭内恒小于零，则实数a 的取值范围是_________. 【答案】1,116⎡⎫⎪⎢⎣⎭【分析】由题意得出()()2log 11a x x ->-对任意的31,2x ⎛⎫∈ ⎪⎝⎭恒成立，然后对底数a 分1a >和01a <<两种情况讨论，结合图象找出关键点得出关于a 的不等式（组）求解，可得出实数a 的取值范围. 【详解】()()()()2222log 2log log 11log 11aa a a a f x x x x x a x x x x =-+=-+--=----， 则不等式()()2log 11a x x ->-对任意的31,2x ⎛⎫∈ ⎪⎝⎭恒成立.当1a >时，312x <<，则1012x <-<，此时()1log 1log log 102a a a x -<<=，则不等式()()2log 11a x x ->-对任意的31,2x ⎛⎫∈ ⎪⎝⎭不成立；当01a <<时，如下图所示：由图象可知，若不等式()()2log 11a x x ->-对任意的31,2x ⎛⎫∈ ⎪⎝⎭恒成立，则20113log 122aa <<⎧⎪⎨⎛⎫≥- ⎪⎪⎝⎭⎩，解得1116a ≤<. 因此，实数a 的取值范围是1,116⎡⎫⎪⎢⎣⎭.故答案为1,116⎡⎫⎪⎢⎣⎭.【点睛】本题考查对数不等式恒成立问题，解题时要注意对底数的取值范围进行分类讨论，并利用数形结合思想得出一些关键点列不等式（组）求解，考查数形结合思想的应用，属于中等题.四、解答题17．已知tan 2.α=求： (1)2sin cos sin 2cos αααα-+；(2)224sin 3sin cos 5cos .αααα--【答案】(1)34(2)1【分析】（1）分子分母同时除以cos α，化为2tan 1tan 2αα-+可得答案.（2）将目标表达式视为分母为22sin cos αα+的分式，再分子分母同时除以2cos α，化为224tan 3tan 5tan 1ααα--+，可得答案.【详解】（1）2sin 12sin cos 2tan 1cos sin sin 2cos tan 22cos αααααααααα---==+++又tan 2α=，所以2tan 12213,tan 2224αα-⨯-==++故2tan 13tan 24αα-=+；（2）222222224sin 3sin cos 5cos 4tan 3tan 54sin 3sin cos 5cos sin cos tan 1ααααααααααααα------==++， 因为tan 2α=，所以22443254sin 3sin cos 5cos 141αααα⨯-⨯---==+， 所以224sin 3sin cos 5cos 1αααα--=. 18．已知函数4()log (41)x f x =- （1）求函数()f x 的定义域； （2）若122x ⎡⎤∈⎢⎥⎣⎦，，求()f x 的值域. 【答案】（1）()0,∞+；（2）[]40,log 15.【分析】（1）根据对数函数的真数大于零，得到不等式，解得；（2）令41x t =-根据122x ⎡⎤∈⎢⎥⎣⎦，求出t 的取值范围，即可求出函数()f x 的值域. 【详解】解：（1）4()log (41)x f x =-410x ∴->解得0x >故函数()f x 的定义域为()0,∞+. （2）令41x t =-，122x ⎡⎤∈⎢⎥⎣⎦，[]115t ∴∈，[]44()log 0,log 15f t t ∴=∈ []4()0,log 15f x ∴∈即函数()f x 的值域为[]40,log 15【点睛】本题考查对数函数的定义域值域的计算问题，属于基础题.19．某企业开发生产了一种大型电子产品，生产这种产品的年固定成本为2500万元，每生产x 百件，需另投入成本()c x （单位：万元），当年产量不足30百件时，()210100c x x x =+；当年产量不小于30百件时，()100005014500c x x x=+-；若每件电子产品的售价为5万元，通过市场分析，该企业生产的电子产品能全部销售完.（利润=总收入-成本）(1)求年利润y （万元）关于年产量x （百件)的函数关系式； (2)年产量为多少百件时，该企业在这一电子产品的生产中获利最大？【答案】(1)2104002500,030100002000,30x x x y x x x ⎧-+-≤<⎪=⎨⎛⎫-+≥ ⎪⎪⎝⎭⎩ (2)当年产量为100百件时，获利最大.【分析】（1）根据“利润=总收入-成本”求得y 关于x 的函数关系式. （2）结合二次函数的性质以及基本不等式求得获利最大时对应的年产量.【详解】（1）依题意，2500101002500,0301000050050145002500,30x x x x y x x x x ⎧---≤<⎪=⎨--+-≥⎪⎩ 2104002500,030100002000,30x x x x x x ⎧-+-≤<⎪⎨⎛⎫-+≥ ⎪⎪⎝⎭⎩. （2）当030x ≤<时，当()40020210x =-=⨯-时，y 取得最大值为210204002025001500-⨯+⨯-=万元.当30x ≥时，10000200020001800x x ⎛⎫-+≤- ⎪⎝⎭万元， 当且仅当10000,100x x x==百件时等号成立. 综上所述，当年产量为100百件时，获利最大. 20．已知函数()21ax bf x x +=+是定义在()1,1-上的奇函数，且1225f ⎛⎫= ⎪⎝⎭ (1)求()f x 的解析式(2)用定义证明()f x 在()1,1-上是增函数 (3)解不等式()()10f t f t -+< 【答案】(1)()21xf x x =+ (2)证明见解析(3)102t t ⎧⎫<<⎨⎬⎩⎭【分析】（1）根据奇函数的性质和所给的条件，代入函数解析式即可； （2）不妨假设()1212,1,1,x x x x ∈-＜ ，判断()()12f x f x - 的符号即可；（3）根据()f x 是奇函数，并是增函数的特点，根据函数定义域即可求出t 的范围. 【详解】（1）由函数()f x 是定义在()1,1-上的奇函数，得()00f =，即0b =，又∵2112225112af ⎛⎫== ⎪⎝⎭⎛⎫+ ⎪⎝⎭，解得1a =， ∴()21xf x x =+； （2）设1x ∀，()21,1x ∈-，且12x x <，则()()()()()()()()()()22122121121212222222121212*********x x x x x x x x x x f x f x x x x x x x +-+---=-==++++++， ∵210x x ->，1210x x -<，2110x +>，2210x +>，∴()()120f x f x -<，即()()12f x f x <， ∴()f x 在()1,1-上是增函数；（3）由()f x 为()1,1-上的奇函数，如()()10f t f t -+<等价于()()1f t f t -<-．则由()f x 在()1,1-上是增函数，可得111111t t t t -<-<⎧⎪-<-<⎨⎪-<-⎩，解得102t <<， 即不等式()()10f t f t -+<的解集为102t t ⎧⎫<<⎨⎬⎩⎭；综上，()21xf x x =+，()()10f t f t -+<的解集为102t t ⎧⎫<<⎨⎬⎩⎭.21．已知角α是第三象限角，且cos cos(2)tan()2()tan()sin()f παπααπααππα⎛⎫--+ ⎪⎝⎭=----. （1）化简()f α；（2）若1sin()5απ-=，求()f α的值； （3）若2310α=-︒，求()f α的值.【答案】（1）()cos f αα=-；（2；（3【解析】（1）利用三角函数诱导公式化简()f α即可.（2）首先根据1sin()5απ-=得到1sin 5α=-，从而得到cos α=()f α的值. （3）首先计算cos cos150α︒==()f α的值. 【详解】（1）cos cos(2)tan()2()tan()sin()f παπααπααππα⎛⎫--+ ⎪⎝⎭=---- sin cos tan cos tan sin αααααα⋅⋅==--⋅. （2）∵1sin()5απ-=，∴1sin 5α=-， ∵α是第三象限角，∴cos α=，∴()cos f αα=-=. （3）∵()231012180150α︒︒︒=-=-⨯+，∴cos cos150α︒==，∴()cos f αα=-=22．已知函数()1421x x f x a a +=-⋅++（1）若2a =，求不等式()0f x <的解集；（2）若(),0x ∈-∞时，不等式()2f x a <-恒成立，求a 的取值范围；（3）求函数()f x 在区间[]1,2上的最小值()h a .【答案】（1）()20,log 3；（2）1,2⎛⎤-∞ ⎥⎝⎦；（3）()253,21,24177,4a a h a a a a a a -≤⎧⎪=-++<<⎨⎪-≥⎩. 【分析】（1）当2a =时，可得出()()()44232123x x x x f x =-⋅+=--，解出2x 的取值范围，进而可求得原不等式的解集；（2）将所求不等式变形为221x a <+，求得当0x <时，()211,2x +∈，根据题意可得出关于实数a 的不等式，进而可求得实数a 的取值范围；（3）当[]1,2x ∈时，令[]22,4x t =∈，()221g t t at a =-++，则问题可等价转化为函数()g t 在[]2,4t ∈上的最小值，然后对实数a 的取值分类讨论，分析出函数()g t 在[]2,4t ∈上的单调性，由此可得出()h a 关于a 的表达式.【详解】（1）当2a =时，可得()()()44232123x x x x f x =-⋅+=--， 由()0f x <，得()()21230x x --<，可得123x <<，解得20log 3x <<， 因此，当2a =时，不等式()0f x <的解集为()20,log 3；（2）因为14212x x a a a +-⋅++<-，即422210x x a a -⋅+-<，()()212210x x a --+<， 0x <，则210x -<，可得2210x a -+>，可得221x a <+，当0x <时，()211,2x +∈，21a ∴≤，解得12a ≤. 因此，实数a 的取值范围是1,2⎛⎤-∞ ⎥⎝⎦； （3）当[]1,2x ∈时，令[]22,4x t =∈，则()221f x t at a =-++，令()221g t t at a =-++，则二次函数()g t 的图象开口向上，该函数的对称轴为t a =.当2a ≤时，()g t 在[]2,4上单调递增，()()min 253g t g a ==-；当24a <<时，()g t 在[]2,a 上单调递减，()g t 在[],4a 上单调递增，()()2min 1g t g a a a ==-++；当4a ≥时，()g t 在[]2,4上单调递减，则()()min 4177g t g a ==-.综上可得：()253,21,24177,4a a h a a a a a a -≤⎧⎪=-++<<⎨⎪-≥⎩. 【点睛】方法点睛：“动轴定区间”型二次函数最值的方法：（1）根据对称轴与区间的位置关系进行分类讨论；（2）根据二次函数的单调性，分别讨论参数在不同取值下的最值，必要时需要结合区间端点对应的函数值进行分析；（3）将分类讨论的结果整合得到最终结果.。

复合函数单调性(专题训练)1.选择题1.函数f(x)的图象大致为（B）。

2.函数y=2x-1的单调递增区间是（B）。

3.函数f(x)=1/x的单调减区间为（D）。

4.已知函数在[1,+∞)上单调递减，则实数a的取值范围是（A）。

5.设函数f(x)=log2(x-a)+log2(x+a)，则使得f(x)≤f(2x-1)成立的x的取值范围是（A）。

6.已知函数f(x)=loga(3-x)，若f(-2)<f(0)，则此函数的单调递增区间是（C）。

7.函数y=|log2x|在区间(k-1,k+1)内有意义且不单调，则k的取值范围是（D）。

8.函数y=x-1在[0,1]上是减函数，则实数a的取值范围是（C）。

9.若函数y=x^2-2x+a有最大值，则a的取值范围为（A）。

10.设函数f(x)在R上为增函数，则下列结论一定正确的是（B）。

11.函数f(x)=log0.5(2-x)+log0.5(2+x)的单调递增区间是（B）。

12.函数y=|log2|x-2||的单调递增区间为（C）。

2.填空题13.已知f(x)=(a^2-2a-2)x是增函数，则实数a的取值范围是(-∞,-1)或(2,+∞)。

14.函数y=(|x|-1)^-1的单调增区间为(-∞,-1)和(1,∞)。

15.函数f(x)=lg(x^2)的单调递减区间是(0,1)。

16.函数f(x)=(x-1)(x-5)的单调递减区间是(1,5)。

17.已知函数y=loga(ax^2-x)在区间[2,4]上是增函数，则实数a的取值范围是(0.5,1)。

18.函数y=(m^2-m-1)是幂函数且在(1,∞)上单调递减，则实数m的值为(φ-1)，其中φ为黄金比例。

19.设f(x)是定义在R上的奇函数，且当x>0时，f(x)=2x。

若对任意的x∈[t,t+1]，不等式f(t)f(t+1)<0成立，则t的取值范围是(-∞,0)。

题目：已知函数f(x)与函数g(x)的图像关于直线y=x对称，且f(x+t)≥g^3(x)恒成立，则实数t的取值范围是什么？解答：根据题目条件，可以得到f(x)与g(x)的图像在y=x这条直线上对称，即f(x)在y=x处的函数值等于g(x)在y=x处的函数值。

1．设()log (1)log (3)(0,1)a a f x x x a a =++->≠，且(1)2f =．(1)求a 的值及()f x 的定义域；(2)求()f x 在区间答案：解答：(1)∵(1)2f =，∴log 42(0,1)a a a =>≠，∴2a =． 由10,30,x x +>⎧⎨->⎩得(1,3)x ∈-，∴函数()f x 的定义域为(1,3)-． (2)22222()log (1)log (3)log (1)(3)log [(1)4]f x x x x x x =++-=+-=--+， ∴当(1,1]x ∈-时，()f x 是增函数；当(1,3)x ∈时，()f x 是减函数．函数()f x 在上的最大值是2(1)log 42f ==，函数()f x 在 ∴()f x 在区间2(1)当5a =时，求函数()f x 的定义域； (2)当函数()f x 的定义域为R 时，求实数a 的取值范围．答案：11,2⎫⎛⎫+∞⎪ ⎪⎭⎝⎭(2)(),4-∞.解答：(1)当5a =时，要使函数()f x 有意义，当1x ≤时，不等式①等价于210x -+>，即 当15x <≤时，不等式①等价于10->，∴无解；当5x >时，不等式①等价于2110x ->，即 综上，函数()f x 的定义域为11,2⎫⎛⎫+∞⎪ ⎪⎭⎝⎭(2)∵函数()f x 的定义域为R ，∴不等式1x -+当且仅当()()150x x --≥时取等号)a 的取值范围是(),4-∞.考点：1.含绝对值不等式的解法；2.不等式的恒成立的问题.3，且当(],1x ∈-∞时()f x 有意义，求实数a 的取值范围． 答案：解答：欲使(),1x ∈-∞时，()f x 有意义，需1240x x a ++>恒成立，(1x ≤)恒成立． 在(),1-∞上是增函数， ∴当1x =时，时，满足题意，即a 的取值范围为 4(0a >且1a ≠)在()1,+∞上的单调性，并予以证明． 答案：当1a >时，()f x 在()1,+∞上为减函数；当01a <<时，()f x 在(1,)+∞上为增函数． 解答：，任取211x x >>，则∵11x >，21x >，∴110x ->，210x ->， 又∵12x x <，∴120x x -<．，即21u u <． 当1a >时，log a y x =是增函数，∴21log log a a u u <，即21()()f x f x <；当01a <<时，函数log a y x =是减函数，∴21log log a a u u >，即21()()f x f x >． 当01a <<时， 5．已知函数()log (3)a f x ax =-(0a >且1a ≠).(1)当[0,2]x ∈时，函数()f x 恒有意义，求实数a 的取值范围；(2)是否存在这样的实数a ，使得函数()f x 在区间[1,2]上为减函数，并且最大值为1？如果存在，试求出a 的值；如果不存在，请说明理由.答案：3(0,1)(1,)2； (2)不存在实数a ，使()f x 在[1,2]上为减函数且最大值为1.解答：(1)由于3y ax =-为减函数，所以要使函数()f x 在[0,2]上恒有意义，因此a 的取值范围是3(0,1)(1,)2； (2)由于3y ax =-为减函数，要使()f x 在[1,2]为减函数且最大值为1，则1a >，且max ()(1)log (3)1a f x f a ==-=，又3y ax =-在[1,2]上需恒大于零，故不存在实数a ，使()f x 在[1,2]上为减函数且最大值为1.6 (1) (2)对于[2,4]x ∈，恒成立，求m 的取值范围. 答案：(1))证明见解答；(2)(0,15)(45,)+∞. 解答：(1)，解得1x <-或1x >， ∴函数的定义域为(,1)(1,)-∞-+∞. 当(,1)(1,)x ∈-∞-+∞时，(2)由[2,4]x ∈时， ①当1a >时，∴对[2,4]x ∈恒成立， ∴0(1)(1)(7)m x x x <<+--在[2,4]x ∈恒成立.设()(1)(1)(7)g x x x x =+--，[2,4]x ∈ 则32()77g x x x x =-++-，∴当[2,4]x ∈时，'()0g x >， ∴()y g x =在区间[2,4]上是增函数，min ()(2)15g x g ==. ∴015m <<. ②当01a <<时，由[2,4]x ∈时，对[2,4]x ∈恒成立. ∴(1)(1)(7)m x x x >+--在[2,4]x ∈恒成立. 设()(1)(1)(7)g x x x x =+--，[2,4]x ∈， 由①可知()y g x =在区间[2,4]上是增函数，max ()(4)45g x g ==，∴45m >. ∴m 的取值范围是(0,15)(45,)+∞.7．已知函数()()24log 23f x ax x =++. (1)已知()11f =,求()f x 单调递增区间;(2)是否存在实数a ,使()f x 的最小值为0？若存在, 求出a 的值; 若不存在, 说明理由. 答案：(1)()1,1-；解答：(1)()()24log 23f x ax x =++且()()2411,log 12131,54,1f a a a =∴+⨯+=∴+=∴=-,可得函数()()24log 23f x x x =-++, 2230,x x -++>∴函数的定义域为()1,3-， 令()222314t x x x =-++=--+可得,当()1,1x ∈-时,t 为关于x 的增函数,底数为41,>∴函数()()24log 23f x x x =-++单调递增区间为()1,1-. (2)设存在实数a ,使()f x 最小值为0. 由于底数为41>,可得真数2231t ax x =++≥恒成立, 且真数t 最小值恰好是1.8．已知函数()()()22lg 32215f x m m x m x ⎡⎤=-++-+⎣⎦，如果函数()f x 的值域为R ，求实数m 的取值范围.答案：解答：令()()()2232215g x m m x m x =-++-+， 如果函数()f x 的值域为R ，则()g x 能取到任意的正数,当2320m m -+=时，即1m =或2.经验证当2m =时适合当2320m m -+≠时据二次函数知识知要使的函数值取得所有正在值只需23200m m ⎧-+>⎨∆≥⎩解之得综上可知满足题意的m 的取值范围是 9．已知函数mx x f x ++=)14(log )(2．(1)若)(x f 是偶函数，求实数m 的值；(2)当0>m 时，关于x 的方程上恰有两个不同的实数解，求m 的范围．答案：解答： (1)若)(x f 是偶函数，则有)()(x f x f =-恒成立，即mx mx x x ++=-+-)14(log )14(log 22，即是x mx 22-=对R x ∈恒成立，故1-=m ；(2)当0>m 时，)14(log 2+=x y ，在R 上单增，mx y =在R 上也单增，所以mx x f x ++=)14(log )(2在R 上单增，且1)0(=f ；又)(x f 单增，得令4222++-=t t y ，又0>m ，故10(1)当7m =时，求函数()f x 的定义域；(2)若关于x 的不等式()2f x ≥的解集是R ，求m 的取值范围．答案： (1) ),4()3,(+∞⋃--∞； (2) ]1-,(-∞解答：(1)不等式的解集是以下不等式组解集的并集：⎩⎨⎧>-++≥7212x x x ，或⎩⎨⎧>+-+<≤72121x x x ，或⎩⎨⎧>+---<7211x x x 解得函数)(x f 的定义域为),4()3,(+∞⋃--∞；(2)不等式2)(≥x f 即R x ∈ 时，恒有R ，m m ,34≤+∴的取值范围是 ]1-,(-∞11．已知a ∈R ，函数 (1)当5a =时，解不等式()0f x >；(2)若关于x 的方程2()log [(4)25]0f x a x a --+-=的解集中恰好有一个元素，求a 的取值范围；(3)设0a >，函数()f x 在区间[,1]t t +上的最大值与最小值的差不超过1，求a 的取值范围.答案：()0,⎫+∞⎪⎭； (2)(]{}1,23,4；解答：(1)()0,⎫+∞⎪⎭． ，()()24510a x a x -+--=， 当3a =时，121x x ==-，经检验，满足题意．当3a ≠且4a ≠时，，21x =-，12x x ≠． 1x 是原方程的解当且仅当，即2a >； 2x 是原方程的解当且仅当，即1a >． 于是满足题意的(]1,2a ∈．综上，a 的取值范围为(]{}1,23,4．(3)当120x x <<时， 所以()f x 在()0,+∞上单调递减．函数()f x 在区间[],1t t +上的最大值与最小值分别为()f t ，()1f t +．即()2110at a t ++-≥，对任意因为0a >，所以函数()211y at a t =++-在区间时，y故a 的取值范围为12(1)若函数内单调递增，求a 的取值范围；(2)求函数在区间[1，2]上的最小值．答案：(1)[)1,+∞；(2) 当1a ≥时，()min 0f x =.解答：(1)由已知，得上恒成立，即 又当 (2)当时，在(1，2)上恒成立， 这时在[1，2]上为增函数(1，2)上恒成立，这时在[1，2]上为减函数),1[)(+∞在区间x f )(x f ),1[0)(+∞≥'在x f 1≥a 0)(>'x f )(x f 0)1()(min ==∴f x f )(x f综上，在[1，2]上的最小值为③当13．已知函数22()lg (32)(1)1f x m m x m x ⎡⎤=-++-+⎣⎦的定义域为R ，求实数m 的取值范围．答案： 1m ≤或解答：∵函数()f x 的定义域为R ，∴对于任意x R ∈，恒有22(32)(1)10m m x m x -++-+>①若2320m m -+=，则2m =或1，当1m =时，不等式即为10>，符合题意，当2m =时，不等式即为210x +>，不恒成立，∴2m =不合题意，舍去．②若2320m m -+≠，由题意得 222320(1)4(32)0m m m m m ⎧-+>⎨∆=---+<⎩，解得，即1m <或综上可得，m 的取值范围是1m ≤或 14．已知函数)1,0(log )(≠>=a a x x f a ，且1)2()3(=-f f ．(1)若)52()23(+<-m f m f ，求实数m 的取值范围；(2)成立的x 的值． 答案：)(x f 0)(,1min =≥x f a 时解答：定义域0+∞（，）上单调递增，所以可得： 3202503225m m m m ->⎧⎪+>⎨⎪-<+⎩，解得(2)15 (1)求函数)(x f 的定义域；(2)求函数)(x f 的值域.答案：(1)(p ,1)；(2)见解答：.解答：(1)要使求函数)(x f 有意义，则得1>x 且p x <， 又因为函数的定义域为非空数集，所以1>p ，所以函数)(x f 的定义域是(p ,1)；，其中p x <<1，，即31≤<p 时， 因为)(x h 在],1[p 上单调递减，且0)1(2)1(>-=p h ，0)(=p h ， 所以)1(log 1)1(2log )(22-+=-<p p x f ； ，即3>p 时， ，0)(=p h ， 所以当p x <<1时，时，即1-<p ，这与1>p 矛盾. 综上所述当31≤<p 时，函数)(x f 的值域是()()1log 1,2-+∞-p ；当3>p 时，函数)(x f 的值域是()]21log 2,(2-+-∞p .16 (1)判断()f x 的奇偶性并证明；(2)若对于[2,4]x ∈，恒有成立，求m 的取值范围． 答案：(1)详见解答；(2)当1>a 时，150<<m ； 当10<<a 时，16>m ．解答：(1)解得11x x <->或所以函数()f x 的定义域为(,1)(1,)-∞-+∞ 函数()f x 为奇函数，证明如下：由(I)知函数()f x 的定义域关于原点对称，又因为所以函数()f x 为奇函数(2) 对[2,4]x ∈恒成立 当10<<a 时，对[2,4]x ∈成立．即(1)(7)x x m +⋅->成立，所以015m << 同理当10<<a 时，，解得16m > 综上所述：当1>a 时，150<<m ,当10<<a 时，16>m17．已知函数2()lg(2)f x ax ax =++ (∈a R )．(1)若1a =-，求()f x 的单调区间；(2)若函数()f x 的定义域为R ，求实数a 的取值范围．答案：(1) ()f x 的单调增区间为(2) 08a ≤<．解答：(1)当1a =-时，2()lg(2)f x x x =--+ 220x x --+>，即220x x +-<，解得：21x -<< 所以函数()f x 的定义域为(2,1)-设2()2,(2,1)t x x x x =--+∈-，则()lg f x t =关于t 在(0,)t ∈+∞为增函数． 由复合函数的单调性，()f x 的单调区间与2()2,(2,1)t x x x x =--+∈-的单调区间一致．二次函数2()2,(2,1)t x x x x =--+∈-的对称轴为所以()t x 在所以()f x 的单调增区间为(2)当0a =时，()lg 2f x =为常数函数，定义域为R ，满足条件． 当0a ≠时，()f x 的定义域为R 等价于220ax ax ++>恒成立． 于是有2080a a a >⎧⎨∆=-<⎩，解得：08a << 综上所述，实数a 的取值范围是08a ≤<．18．已知函数()ln(3)ln(3)f x x x =++-．(1)求函数()y f x =的定义域；(2)判断函数()y f x =的奇偶性；(3)若(21)()f m f m -<，求m 的取值范围．答案： (1)()3,3-；(2)函数()f x 为偶函数； 或12m <<． 解答：(1)303330x x x +>⎧⇒-<<⎨->⎩，所以定义域为()3,3-； (2))()3ln()3ln()(x f x x x f =++-=-)(x f ∴为偶函数；(3)因为()()()()2ln 3ln 3ln 9f x x x x=++-=- 可知)(x f 在]3,0[上为减函数，又为偶函数则原不等式可化为⎪⎩⎪⎨⎧>-<<-<-<-|||12|333123m m m m 解得或12m <<．。

1．已知20.5()log ()f x x mx m =--．(1)若函数()f x 的值域为R ，求实数m 的取值范围；(2)若函数()f x 在区间上是增函数，求实数m 的取值范围． 答案：(1)0m ≥或4m ≤-；解答：(1)∵()f x 值域为R ，令2()g x x mx m =--，则()g x 取遍所有的正数，240,0m m m ∴∆=+≥∴≥或4m ≤-；(2)2．已知函数9()log (91)()xf x kx k R =++∈是偶函数.(1)求k 的值；(2)的图象与()f x 的图象有且只有一个公共点，求a 的取值范围.答案： (2){3}(1,)-+∞.解答：令3x t =，则(0,)t ∈+∞，有且只有一个正实根t ，当10a -≠时，若0∆=，则3a =-或 时，根20t =-<，舍去.3a =-时，根为 若0∆>，则120t t <，解得1a >， 从而所求a 的范围是{3}(1,)-+∞.考点：函数的奇偶性，换元法，一元二次方程根的分布．3. (1)求m 的值，并求f (x)的定义域； (2)判断函数)(x f 的单调性，不需要证明；(3)是否存在实数λ,使得不等式若存在,求出实数λ的取值范围;若不存在,请说明理由. 答案： (1))1,1(-；(2))(x f 在定义域内单调递增；(3)解答：(1)为奇函数，)()(x f x f -=-∴在定义域内恒成立，111-==-=∴m m m （舍去），即或，故函数的定义域是)1,1(-； ，任取1121<<<-x x ，∵1121<<<-x x ，0)()(21<-x u x u ，∴)(lg )(lg 21x u x u >，),()(21x f x f <∴即)(x f 在定义域内单调递增；由(1)，(2)知当θ=0时成立； sinθ=t,4(1)若的定义域为，求实数的取值范围； (2)当时，求函数的最小值；(3)是否存在非负实数m 、n,的定义域为[]n m ,，值域为[]n m 2,2，若存在，求出、的值；若不存在，则说明理由．答案：(3)2,0==n m ．2(2)g mx x m ++R m []1,1x ∈-[]2()2()3y f x af x =-+)(a h m n解答：令 ,当,的定义域为，不成立； 当，R ，∴，解得，综上所述，，对称轴为，当 时，a t =时，()2min 3a y a h -==； 当2>a 时，2=t 时，()a y a h 47min -==．由题意，知⎩⎨⎧==n n m m 2222解得⎩⎨⎧==20n m ，∴存在2,0==n m ，使得函数的定义域为，值域为．m x mx u ++=22时0=m x u 2=），（∞+0时0≠m ⎩⎨⎧<-=∆>04402m m 1>m 1>m ]1,1[-∈x a t =]2,0[]4,0[5(0>a ，1≠a )． (1)当1>a 时，讨论()f x 的奇偶性，并证明函数()f x 在()1,+∞上为单调递减； (2)当(),2∈-x n a 时，是否存在实数a 和n ，使得函数()f x 的值域为()1,+∞，若存在，求出实数a 与n 的值，若不存在，说明理由． 答案：(1)奇函数，证明见解答：；解答：(1)()f x 的定义域为{}|11x x x ><-或关于原点对称， ，∴()f x 为奇函数， 法1：当1a >时，设121x x <<，则()(()(1111x x +-又1a >，，()()12f x f x ∴>，∴函数()f x 在(1,)+∞上为减函数 法2：当1a >时，设121x x <<，令，所以12log log a a t t >，∴函数()f x 在(1,)+∞上为减函数 (2)，(),2∈-x n a①当1a >时，要使()f x 的值域为(1,)+∞，则须(,)t a ∈+∞，②当01a <<时，(0,)t a ∈，则，当(),2∈-x n a 时，函数()f x 的值域为()1,+∞．6．已知函数()2log 1f x x =-的定义域为[]1,16，函数()()()222g x f x af x =++⎡⎤⎣⎦． (1)求函数()y g x =的定义域； (2)求函数()y g x =的最小值；(3)若函数()y g x =的图象恒在x 轴的上方，求实数a 的取值范围． 答案： (1)[]1,4；(2)()2min3-,12,1133,1a a g x a a a a a ≥⎧⎪=-++-<<⎨⎪+≤-⎩； (3)()1,3a ∈-． 解答：(1)2116116x x ≤≤⎧⎨≤≤⎩，14x ∴≤≤，即函数()y g x =的定义域为[]1,4． (2)()()()()222222log 22log 3g x f x af x x a x a =++=+--+⎡⎤⎣⎦．令[]2log ,0,2t x t =∈，则()()22222212y t a t a t a a a =+--+=---++⎡⎤⎣⎦．当1a ≥时，y 在[]0,2上是增函数，所有min 0,3t y a ==-； 当-11a <<时，y 在[]0,1a -上是减函数，[]1,2a -上是增函数，所有2min 1,2t a y a a =-=-++；当1a ≤-时，y 在[]0,2上是减函数，所有min 2,33t y a ==+．综上，()2min3-,12,1133,1a a g x a a a a a ≥⎧⎪=-++-<<⎨⎪+≤-⎩． (3)由题知，()0g x >恒成立，即()min 0g x >()min 0g x >． 当1a ≥时， min 30,13y a a =->∴≤<；当-11a <<时， 2min 20,11y a a a =-++>∴-<<；当1a ≤-时， min 330,y a a =+>∴无解 综上，()1,3a ∈-．7．已知函数)0(1)1()(2>++=-a a x g x 的图象恒过定点A ，且点A 又在函数(1)求实数a 的值； (2)(3)的图象与直线b y 2=有两个不同的交点时，求b 的取值范围． 答案：(1)1a =；解答：(1)函数()g x 的图像恒过定点A ，A 点的坐标为(2，2)，又因为A 点在()f x 上，图象与直线b y 2=021b << ，故b 的取值范围为8．已知函数2()log (1)f x x =+，当点(,)x y 在函数()y f x =的图象上运动时，函数()y g x =(的图象上运动． (1)求函数()y g x =的解析式； (2)求函数()()()F x f x g x =-的零点．(3)函数()F x 在(0,1)x ∈上是否有最大值、最小值；若有，求出最大值、最小值；若没有请说明理由． 答案：解答：解得0x =或1x =，∴函数()F x 的零点0x =或1x =； (3)设31m x =+，由(0,1)x ∈得(1,4)m ∈，函数在(1,2]上递减，在[2,4)上递增，当2m =时有最小值4，无最大值，∴t 有最小值∴函数()F x 在(0,1)x ∈内有最小值9 (1)讨论函数()f x 的单调性；(2)若对于任意的[)()()1,,1x f x a x ∈+∞≥-恒成立，求a 的范围． 答案：(1)()f x 在()0,1上递减,在()1,+∞上递增； (2)2a ≤． 解答：， ()f x 在()1,+∞上递增；()()'0,1f x 在递增,()()()()''120,0,1f x f f x <=-<在上递减，所以()f x 在()0,1上递减,在()1,+∞上递增．(2) ()()()()()()1,1ln ,11ln 10x f x x x f x a x x x a x ≥=+≥-⇔+--≥由(1)知,()()'1,g x +∞在上递增,()()''12g x g a ≥=- 若20,2a a -≥≤即,()()[)'01,g x g x ≥+∞，在上递增,()()10,g x g ∴≥=所以不等式成立2a >若,存在()()001,,'0x g x ∈+∞=使得,当0[1,)x x ∈时,综上所述，2a ≤．10(1)当4=a 时，求函数)(x f 的定义域；(2)若对任意的R x ∈，都有2)(≥x f 成立，求实数a 的取值范围． 答案：(1){}11|>-<x x x 或；解答： (1)，即2-<x，即1>x 综上所述，函数()x f 的定义域为{}11|>-<x x x 或 (2)11(1)(2)若关于x 的不等式()()2520f x ax f x a -++++<对任意实数[]2,3x ∈恒成立，求实数a 的取值范围．答案： (1)7m =；解答：(1)由()f x 是奇函数得：()()f x f x -=-，所以 即227m =，7m =±； 得定义域为()7,7-．∴7m =． 是增函数，∴()f x 在()7,7-是增函数．又()f x 为奇函数，∴()()252f x ax f x a -->+，∴27257x a x ax -<+<--<对任意实数 []2,3x ∈恒成立；对于225x a x ax +<--，即()252x x a x -->+，20x +>，∴(23x ≤≤)， 设2t x =+，则2x t =-，且45t ≤≤，对于72x a -<+，()2h x x a =+在[]2,3上递增，∴()()min 2227h x h a ==+>-，则对于257x ax --<，即()2F 120x x ax =--<，∴()()F 2280F 3330a a =--<⎧⎪⎨=--<⎪⎩，则1a >-； 综上，a 的取值范围是 12．定义在D 上的函数()f x ，如果满足：对任意x D ∈，存在常数0M ≥，都有|()|f x M ≤成立，则称()f x 是D 上的有界函数，其中M 称为函数()f x的一个上界．已知函数(1)若函数()g x 为奇函数，求实数a 的值；(2)在(1)的条件下，求函数()g x 在区间(3)若函数()f x 在[0,)+∞上是以5为上界的有界函数，求实数a 的取值范围． 答案： (1)1a =-； (2)[3,)+∞； (3)[7,3]-．解答：(1)因为函数()g x 为奇函数， 所以()()g x g x -=-，即 ，得1a =±，而当1a =时不合题意，故1a =-．(2)由(1)，易知()g x 在区间(1,)+∞上单调递增，上的值域为[3,1]--，所以|()|3g x ≤，故函数()g x 在区间上的所有上界构成集合为[3,)+∞．(3)由题意知，|()|5f x ≤在[0,)+∞上恒成立， ，得1t ≥． 易知()P t 在[1,)+∞上递增，设121t t ≤<， 所以()h t 在[1,)+∞上递减， ()h t 在[1,)+∞上的最大值为(1)7h =-，()p t 在[1,)+∞上的最小值为(1)3p =， 所以实数a 的取值范围为[7,3]-．。

复合对数函数的单调性问题一、求复合对数函数的单调区间常借助于复合函数的单调性规律“同增异减”来求其单调区间.例1.求函数()2log 32a y x x =+-的单调区间.分析: 可视函数()2log 32a y x x =+-由外函数log a y u =和内函数232u x x =+-复合而成, 其中外函数的单调性不确定，需讨论; 内函数处在真数位置，函数值只能取正数.解: 函数的定义域为{}2|320x x x +->,即()1,3-.内函数232u x x =+-在区间()1,3-上的增区间为(-1,1],减区间为[1,3).外函数log a y u =的单调性由a 决定.当a>1时,外函数log a y u =单调增,此时原函数的增区间为(-1,1],减区间为[1,3);当0<a<1时,外函数log a y u =单调减,此时原函数的增区间为[1,3),减区间为(-1,1].评注: 研究单调性，首先应考察函数的定义域.二、已知复合对数函数的单调性求参数 ()()2121log ,,.2f x x ax a a ⎛⎫=---∞- ⎪⎝⎭例2.函数在区间上是增函数求实数的取值范围 分析: 根据题意,需保证函数()2g x x ax a =--在1,2⎛⎫-∞- ⎪⎝⎭上单调递减且有意义,即函数值恒大于零. ()2:,g x x ax a =--解令由()()12log f x g x =在1,2⎛⎫-∞- ⎪⎝⎭上为增函数, 可得函数g(x)在1,2⎛⎫-∞- ⎪⎝⎭上为减函数,且g(x)>0在1,2⎛⎫-∞- ⎪⎝⎭上恒成立. 故1221,1.1202a a g ⎧≥-⎪⎪-≤≤⎨⎛⎫⎪-≥ ⎪⎪⎝⎭⎩解得故实数a 的取值范围是[-1,1].2 评注: 1.处理此类问题时,通常先保证单调性,后保证有意义.对本题而言,若先保证()2g x x ax a =--在1,2⎛⎫-∞- ⎪⎝⎭上有意义,即函数值恒大于零,则需通过分类讨论来保证g(x)的最小值大于零,比较麻烦; 2.12g ⎛⎫- ⎪⎝⎭并不是函数()2g x x ax a =--在1,2⎛⎫-∞- ⎪⎝⎭上的最小值, 而是极小值, 故需保证10.2g ⎛⎫-≥ ⎪⎝⎭例3.是否存在实数a,使函数()()2log a f x ax x =-在区间[2,4]上是增函数？如果存在,求出a 的变化范围;如果不存在,请说明理由.分析:本题属存在性问题,通常假设存在,再结合条件分析,若得出矛盾,则不存在;若无矛盾,则可得出结果. ()()()[]()[]()()()[]()[]()22222:,log 2,4,2,421,,1224201log 2,4,2,44416a a g x ax x a ax x g x ax x a a g a a ax x g x ax x g =-=-=-⎧≤⎪>>⎨⎪=->⎩∴>=-=-≥=解设假设符合条件的存在.当a>1时,为使函数f x 在区间上是增函数只需在区间上恒正且单调递增,1x=故应满足2a 解得又当0<a<1时,为使函数f x 在区间上是增函数只需在区间上恒正且单调递减,1x=故应满足2a ()()[]2,40log 2,4a a ax x ⎧⎪⎨⎪->⎩=-此不等式组无解.综上可知,当a>1时函数f x 在区间上为增函数.评注: 例3比例2更具一般性. ()9log 8[1,),.a f x x a x ⎛⎫=+-+∞ ⎪⎝⎭例4.函数在上单调递增求实数的取值范围 ()()()()()()()9:log 8[1,)0[1,)8[1,)01,938[1,)a f x x x a x x a a x x ⎛⎫=+-+∞ ⎪⎝⎭⎧>+∞⎪⎪⎨⎪=+-+∞⎪⎩⎧>⎪⎪<⎨⎪=+-+∞⎪⎩解要使函数在上单调递增,a x+8-在上恒成立,x 只需保证g x 在上单调递增,a 1+8-,1即解1得g x 在上单调递增2, ()()()()()()12121212121212121212121,88100,10,1,,143,4:1,9).a a a x x g x g x x x x x x x x x a x x a x x x x x x a x x a a ⎛⎫⎛⎫≤<-=+--+-=-+< ⎪ ⎪⎝⎭⎝⎭-<∴+>>-≤<>-≥-设则即要使恒成立只要由得的范围是[- 评注: 1.本题应用单调性的定义来保证函数()8a x x =+-g x [1,)+∞在上单调递增,将其转化为恒成立问题; 2.也可以借助于函数()a h x x x=-(分a>0,a<0,a=0三种情况)的单调性规律来求a 的范围.。

4.4 对数函数1．对数函数的定义一般地，我们把函数y＝log a x(a＞0，且a≠1)叫做对数函数，其中x是自变量，函数的定义域是(0，＋∞).(1)由于指数函数y＝a x中的底数a满足a＞0，且a≠1，则对数函数y＝log a x中的底数a也必须满足a＞0，且a≠1.(2)对数函数的解析式同时满足：①对数符号前面的系数是1；②对数的底数是不等于1的正实数(常数)；③对数的真数仅有自变量x.2．对数函数的图象和性质一般地，对数函数y＝log a x(a＞0，且a≠1)的图象和性质如下表所示：a＞10＜a＜1图象性质定义域：(0，＋∞)值域：R图象过定点(1,0)，即当x＝1时，y＝0在(0，＋∞)上是增函数在(0，＋∞)上是减函数非奇非偶函数3.反函数对数函数y＝log a x(a＞0，且a≠1)和指数函数y＝a x(a＞0，且a≠1)互为反函数，它们的图象关于直线y＝x 对称．4．对数型复合函数的单调性复合函数y＝f[g(x)]是由y＝f(x)与y＝g(x)复合而成，若f(x)与g(x)的单调性相同，则其复合函数f[g(x)]为增函数；若f(x)与g(x)的单调性相反，则其复合函数f[g(x)]为减函数.对于对数型复合函数y＝log a f(x)来说，函数y＝log a f(x)可看成是y＝log a u与u＝f(x)两个简单函数复合而成的，由复合函数单调性“同增异减”的规律即可判断．另外，在求复合函数的单调区间时，首先要考虑函数的定义域．5．对数型复合函数的值域对于形如y＝log a f(x)(a>0，且a≠1)的复合函数，其值域的求解步骤如下：(1)分解成y＝log a u，u＝f(x)两个函数；(2)解f(x)>0，求出函数的定义域；(3)求u的取值范围；(4)利用y＝log a u的单调性求解．题型一 对数函数的判断例1、（1）给出下列函数：①223log y x =；①3log (1)y x =-；①(1)log x y x +=；①log e y x =.其中是对数函数的有（ ） A ．1个B ．2个C ．3个D ．4个（2）若函数2log 32a y x a a =+-+为对数函数，则a =（ ）A ．1B ．2C ．3D ．4解:（1）①①不是对数函数，因为对数的真数不是仅有自变量x ； ①不是对数函数，因为对数的底数不是常数；①是对数函数．（2）由题可知：函数2log 32a y x a a =+-+为对数函数所以23201a a a -+=⇒=或2a =，又0a >且1a ≠所以2a = 跟踪练习1．下列函数表达式中，是对数函数的有（ ）①y ＝log x 2；①y ＝log a x (a ①R )；①y ＝log 8x ；①y ＝ln x ；①y ＝log x (x ＋2)；①y ＝log 2(x ＋1)． A ．1个B ．2个C ．3个D ．4个【解析】形如log a y x =（0a >且1a ≠）的函数为对数函数，故①①为对数函数，所以共有2个. 2．下列函数表达式中，是对数函数的有（ ）①log 2x y =；①()log a y x a =∈R ；①8log y x =；①ln y x =；①()log 2x y x =+；①42log y x =；①()2log 1y x =+. A ．1个 B ．2个 C ．3个D ．4个【解析】由于①中自变量出现在底数上，∴①不是对数函数； 由于①中底数a ∈R 不能保证0a >，且1a ≠，∴①不是对数函数； 由于①①的真数分别为()2x +，()1x +，∴①①也不是对数函数； 由于①中4log x 的系数为2，∴①也不是对数函数； 只有①①符合对数函数的定义.3．（全国高一课时练习）若函数()2()log 45a f x x a a =+--是对数函数，a =_________.【解析】由对数函数的定义可知，245001a a a a ⎧--=⎪>⎨⎪≠⎩，解得5a =．题型二 对数函数的解析式或函数值例2（1）（上海高一专题练习）对数函数的图像过点M (125，3)，则此对数函数的解析式为（ ） A ．y ＝log 5xB ．y ＝15log xC ．y ＝13log xD ．y ＝log 3x（2）（全国高一课前预习）设()log a f x x =（0a >且1a ≠），若1(2)2f =，则12f ⎛⎫= ⎪⎝⎭（ ）. A ．2B ．2-C ．12-D ．12【解析】（1）设函数解析式为y ＝log a x (a >0，且a ≠1)．由于对数函数的图像过点M (125，3)， 所以3＝log a 125，得a ＝5.所以对数函数的解析式为y ＝log 5x . （2）因为()log a f x x =（0a >且1a ≠），1(2)2f =，所以1(2)log 22a f ==，即122a =，解得4a =， 所以4()log f x x =，所以4111log 222f ⎛⎫==- ⎪⎝⎭.跟踪练习1．若某对数函数的图象过点()4,2，则该对数函数的解析式为（ ） A ．2log y x =B ．42log y x =C ．2log y x =或42log y x =D ．不确定【解析】设函数为()log 0,1a y x a a =>≠，依题可知，2log 4a =，解得2a =，所以该对数函数的解析式为2log y x =．2．若函数()()lo 1g a f x x =+(0,1)a a >≠的图像过点(7,3)，则a 的值为（ ） A 2B ．2C ．22D ．12【解析】由题, ()373log 182a a a +⇒=⇒==.题型三 对数函数的定义域例3（1）函数()ln 14x f x x-=-的定义域为（ ）A ．(]1,2B ．[]1,4C ．()1,4D ．[]2,4（2）已知函数(2)x y f =的定义域是[]1,1-，则函数3(log )f x 的定义域是（ ） A ．[]1,1-B ．1,33⎡⎤⎢⎥⎣⎦C ．[]1,3D ．[3,9]（3）若函数()lg 1y ax =+的定义域为(),1-∞，则a =（ ） A ．1 B ．－1 C ．2D ．无法确定【解析】（1）对于函数()ln 14x f x x -=-1040x x ->⎧⎨->⎩，解得14x <<.因此，函数()ln 14x f x x-=-的定义域为()1,4.（2）由[]1,1x ∈-，得1,222x⎡⎤∈⎢⎥⎣⎦，所以31log ,22x ⎡⎤∈⎢⎥⎣⎦，所以3,9x ⎤∈⎦． （3）函数()lg 1y ax =+的定义域为(),1-∞，则10ax +>的解集为(),1-∞， 即0a <，且10ax +=的根11a-=，故1a =-. 跟踪练习1．函数()00.5log 21y x =-⎡⎤⎣⎦的定义域为（ ）A ．1,12⎛⎫⎪⎝⎭B ．1,2⎛⎫+∞ ⎪⎝⎭C ．()1,+∞D ．()1,11,2⎛⎫+∞ ⎪⎝⎭【解析】要使函数有意义，只需()0.5log 210x -≠，即210211x x ->⎧⎨-≠⎩，解得112x <<或1x >． 2．函数3()log (21)1xf x x x =--的定义域是（ ） A ．1,12⎛⎤ ⎥⎝⎦B ．1,12⎡⎤⎢⎥⎣⎦C ．(1,)+∞D ．1(,1)2【解析】由已知得1021>0x x ->⎧⎨-⎩，解得112x <<，所以函数()f x 的定义域为112⎛⎫⎪⎝⎭， 3．若函数(1)f x +的定义域为[0 1]，，则(lg )f x 的定义域为（ ） A ．[10 100]，B ．[1 2]，C ．[0 1]，D ．[0 lg2]，【解析】因为函数(1)f x +的定义域为[0 1]，，所以112x ≤+≤，所以1lg 2x ≤≤， 解得：10100x ≤≤，所以(lg )f x 的定义域为[10 100]，. 4.求下列函数的定义域 （1）2112y x x=+-- （2）函数221()x f x --=（3）20()(54)lg(43)x f x x x =+-+ 【解析】（1）若要使函数有意义，则22010x x ⎧-≠⎪⎨-≥⎪⎩，解得1≥x 或1x ≤-且2x ≠±，所以该函数的定义域为][)()(,2)(2,11,22,-∞-⋃--⋃⋃+∞；（2）若要使函数有意义，则2210log (1)010x x x ⎧--≥⎪-≠⎨⎪->⎩，解得3x ≥，所以该函数的定义域为[)3,+∞；（3）若要使函数有意义，则lg(43)0430540x x x +≠⎧⎪+>⎨⎪-≠⎩，解得34x >-且12x ≠-，45x ≠，所以该函数的定义域为31144,,,42255⎛⎫⎛⎫⎛⎫--⋃-⋃+∞ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.题型四 对数函数的定点例4函数()log 272=+-a y x （0a >，且1a ≠）的图象一定经过的点是（ ） A ．7,22⎛⎫-- ⎪⎝⎭B ．()3,2--C ．()3,1--D ．()4,2--【解析】令271x +=，3x =-，则2y =-，即函数图象过定点()3,2--． 跟踪练习1．函数()()log 310,1a y x a a =->≠的图象过定点（ ） A ．2,13⎛⎫ ⎪⎝⎭B ．()1,0-C ．2,03⎛⎫ ⎪⎝⎭D ．()0,1-【解析】对于函数()()log 310,1a y x a a =->≠，令311x -=，可得23x =，则log 10a y ==， 因此，函数()()log 310,1a y x a a =->≠的图象过定点2,03⎛⎫⎪⎝⎭.2．函数()log 1a y x =-的图象必过的点是（ ） A ．()1,0- B ．()1,0C ．()0,0D ．()2,0【解析】() log 1a y x =-，则当11x -=，即2x =时，0y =是与a 的值无关的定值，故函数()log 1a y x =-的图形必过的点是()20,.3．（湖北高一开学考试）已知函数log (3)2a y x =-+（0a >且1a ≠）的图象恒过定点P ，点P 在幂函数()y f x =的图象上，则lg (4)lg (25)f f +=（ ) A ．2-B ．2C ．1D ．1-【解析】函数()log 32a y a =-+中，令31x -=，解得4x =，此时log 122a y =+=；所以函数y 的图象恒过定点()4,2P ，又点P 在幂函数()my f x x ==的图象上，所以42m =，解得0.5m =；所以()0.5f x x =，所以()()()()lg 4lg 25lg 425lg101f f f f +=⋅==⎡⎤⎣⎦．题型五 对数函数的值域（最值）例5（1）已知184x ≤≤，则函数2()log f x x =的值域是 。

对数函数比较大小及复合函数的单调性一、单选题(共10道，每道10分)1.设，则( )A.b<a<cB.c<a<bC.c<b<aD.a<c<b答案：B解题思路：试题难度：三颗星知识点：基本初等函数值大小的比较2.设，则( )A.a>b>cB.b>a>cC.b>c>aD.c>a>b答案：B解题思路：试题难度：三颗星知识点：基本初等函数值大小的比较3.已知，则( )A.a＝b<cB.a<b<cC.a＝c>bD.a>c>b答案：C解题思路：试题难度：三颗星知识点：基本初等函数值大小的比较4.设，，，则( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：对数值大小的比较5.已知函数是定义在上的偶函数，当时，是减函数，若，则( )A.a>b>cB.c>b>aC.c>a>bD.a>c>b答案：B解题思路：试题难度：三颗星知识点：基本初等函数值大小的比较6.已知函数在上是增函数，则a的取值范围是( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：对数函数的单调性7.函数上为减函数，则a的取值范围是( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：对数函数的单调性8.函数的单调递增区间是( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：对数函数的单调性9.若函数有最小值，则a的取值范围是( )A.0<a<1B.0<a<2且a≠1C.1<a<2D.a≥2答案：C解题思路：试题难度：三颗星知识点：对数函数的单调性10.定义在上的偶函数在上递增，，则满足的x 的取值范围是( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：对数函数图象与性质的综合应用。