41立体形与平面图形(1)
- 格式:doc
- 大小:25.50 KB
- 文档页数:1


4.1.1 立体图形与平面图形第1课时教学设计教学目标1.通过观察实物和具体的模型,了解基本的几何图形概念,并能够识别.2.通过用数学的眼光观察世界,欣赏世界,体会学习几何知识的重要意义和应用价值.3.感受几何的美,形成对学习几何图形的渴望和浓厚兴趣.教学重点识别一些基本的几何图形.教学难点了解从实物外形抽象出来的几何图形的概念.教学过程一、情境引入1.我们已经学习了很多图形,丰富多彩的世界中包含着形态各异的图形.在下面的图片中,你能找到一些熟悉的图形吗?(欣赏大美重庆的图片)2.你还记得小学学过的一些图形吗?三角形、正方形、长方形、圆、菱形、梯形、圆柱、正方体、长方体. 还有:圆锥、球、线段、点等,都是从形形色色的物体外形中得出的,它们都是几何图形.二、合作探究探究一:那你能将这些常见的几何图形分类吗?平面图形:立体图形:你的分类依据是什么?各部分都在同一平面内的几何图形是平面图形.常见的还有:点、线段、角、四边形、多边形等.各部分不都在同一平面内的几何图形是立体图形.常见的还有:棱柱、棱锥、圆台等.探究二:1.你能看出这些实物的形状对应哪些几何图形吗?球正方体长方体圆锥六棱柱四棱锥三棱柱六棱柱四棱锥2.这些图片中包含哪些简单的几何图形?探究三:1.看一看、摸一摸、说一说:请大家看看自己手里的几何图形,摸一摸,说说它们都有什么特征.2.找一找你能在教室里面找出它们相应的实物吗?3.做一做利用自己身边现有的几何图形,拼一拼,看看会出现什么新图形.三、课堂练习出示课本第116页练习:第1题、第2题.3.如图所示,各标志的图案主要由哪些简单的平面图形组成?四、课堂小结谈谈你本节课的收获:几何图形:1.平面图形 2.立体图形学习了这节课,你有什么想法?(引导学生说出自己这节课的感受,以及对未来的一些美好设想)五、作业布置见精准作业布置单六、板书设计。
![4[1]11立体图形与平面图形1](https://uimg.taocdn.com/2d8b5b0c02d276a201292e40.webp)
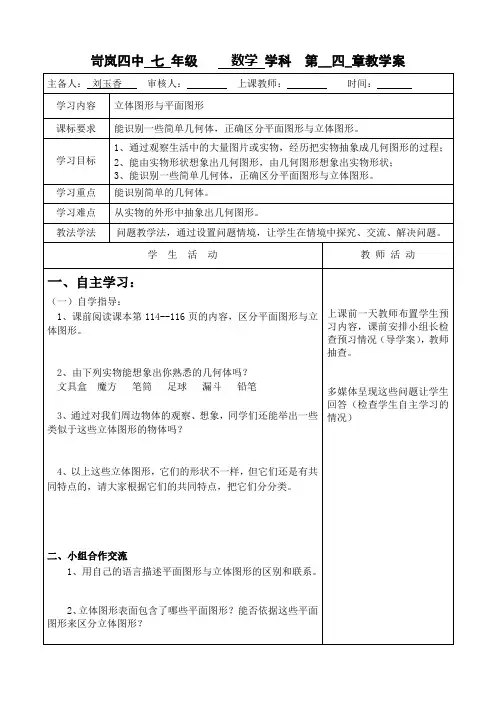



立体图形与平面图形一、立体图形1. 柱体棱柱:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫棱柱.圆柱:以矩形的一边所在直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫做圆柱.2. 锥体棱锥:有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫棱锥.圆锥:以直角三角形一直角边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫圆锥.3. 球体半圆以它的直径为旋转轴,旋转所成的曲面所围成的几何体叫球体.4. 多面体围成棱柱和棱锥的面是平的面,像这样的立体图形叫多面体.棱柱有三棱柱、四棱柱、五棱柱等.棱锥也有三棱锥、四棱锥、五棱锥等.二. 画立体图形1. 三视图法从正面、上面和侧面(左面或右面)三个不同的方向看一个物体,然后描绘三张所看到的图,即视图,这样就把一个物体转化为平面的图形.从正面看到的图形称为正视图;从上面看到的图形称为俯视图;从侧面看到的图形称为侧视图,按观察方向不同,有左视图,右视图.注:⑴正视图与俯视图的长度相等,且相互对正,即“长对正”;⑵正视图与侧视图的高度相等,且相互平齐,即“高平齐”;⑶俯视图与侧视图的宽度相等,即“宽相等”.2. 欧拉公式多面体具有的顶点数,棱数和面数满足欧拉公式:顶点数+面数-棱数=2三、柱体、锥体的展开名称几何体图形平面展开图底面形状侧面展开形状正方体正方形长方形圆锥圆扇形圆柱圆长方形四、常见几何体的主视图【典型例题】例1. 下列说法是否正确?正确的打“√”,不正确的打“×”,并简要说明理由.(1)柱体的上、下两个面一样大(2)圆柱和圆锥的底面都是圆,圆柱的侧面是长方形,圆锥的侧面是三角形(3)棱柱的底面是四边形,侧面可能是三角形(4)棱锥的侧面都是三角形(5)球体、圆柱、圆锥都不是多面体.分析:要对以上各种说法作出正确的判断,应从熟悉柱体、锥体、球体这些立体图形入手,把握它们各自的特征,弄清它们之间的区别.解:(1)√.柱体包括圆柱和棱柱.圆柱的两个底面都是大小一样的圆,棱柱两个底面都是一样大的三角形或多边形.(2)×.圆柱和圆锥的侧面都是弯曲的面.而长方形、三角形都是平的面,两者显然有区别.(3)×.棱柱的底面除了四边形以外,还可以是三角形等其它图形,棱柱的侧面都是四边形.(4)√.棱锥的所有棱都交于一点,侧面都是三角形.(5)√.多面体都是由平的面围成的立体图形,而球体、圆柱、圆锥并不都是由平面围成的.说明:留心生活中的物体,并能从中抽象出立体图形,除了注意不同类立体图形的区别,更应注意同类立体图形的细微差别.例2. 能否组成一个22条棱,10个面,15个顶点的棱柱或棱锥?为什么?分析:本题很难利用图形作出判断、考虑到棱柱或棱锥都是多面体,多面体都应满足“欧拉公式”.解:根据欧拉公式,顶点数+面数-棱数=2+-=当顶点数为15,面数为10时,棱数应为:1510223因此,不能组成一个棱数为22,面数为10,顶点数为15的棱柱或棱锥.说明:欧拉公式体现了多面体中顶点数、面数与棱数之间的关系,已知其中的两个数就可以求出第三个数.另外,还可以用它来判断具有某些条件的多面体是否存在.例3. 填空正方体是由_________个顶点,_________条棱,_________个面组成的,它还具有以下特点(写出三个)___________________________.解:正方体是由8个顶点,12条棱,6个面组成的,它还具有以下特点:所有的棱都相等,所有的面都是正方形,它是一个多面体.(或柱体、四棱柱等)例4. 用火柴摆出正方形,用多少根火柴才能摆出6个正方形?尽可能多地设想各种方案.并画出你的图形.(要求摆出的6个正方体的边长限于一根火柴的长)解:第一种方法:摆平面图形需要用17根火柴.第二种方法:摆三棱柱需要用15根火柴.第三种方法:摆正方体需要用12根火柴.例5.如图,下面是一个物体的三视图,试描述该物体的形状.正视图左视图俯视图分析:由物体的三视图想象物体的形状,要几个视图联系起来看.从正视图中可看出它是由两个部分叠加或是左边挖掉了一个形体,再对照俯视图,左视图便可知道右边上面加了半个圆柱体,圆柱下面是一个长方体,并且圆柱体的左面与长方体左面平齐,柱体的底面直径与长方体的宽一样.解:该物体的形状如图所示:说明:由视图想象物体的形状一般按以下步骤进行:(1)分线框,把几个视图联系起来看,把物体大致分成几部分;(2)识形体,定位置,根据每一部分的视图想象出它的形体,并确定它们的相互位置;(3)综合起来想整体,确定各个部分的形体及相互位置后,整个物体的形状也就清楚了.例6. 如图所示是一个几何体的两个视图,求该几何体的体积( 取3.14,长度单位cm )2032402530正视图 俯视图分析:从所给两个视图可以确定,设几何体是由两部分组成的,下面是一个长方体,它的长、宽、高分别是30cm 、25cm 、40cm.上面是一个圆柱体,底面圆的直径是20cm ,长为32cm ,所以该几何体的体积是这两部分体积之和.解:长方体体积为:30×25×40=30000cm3圆柱体体积为:3.14×102×32=10048 cm 3 30000+10048=40048cm 3答:几何体体积为400483cm .例7. 如图所示的立方体,将其展开得到的图形是( )A B C D (例8图)。



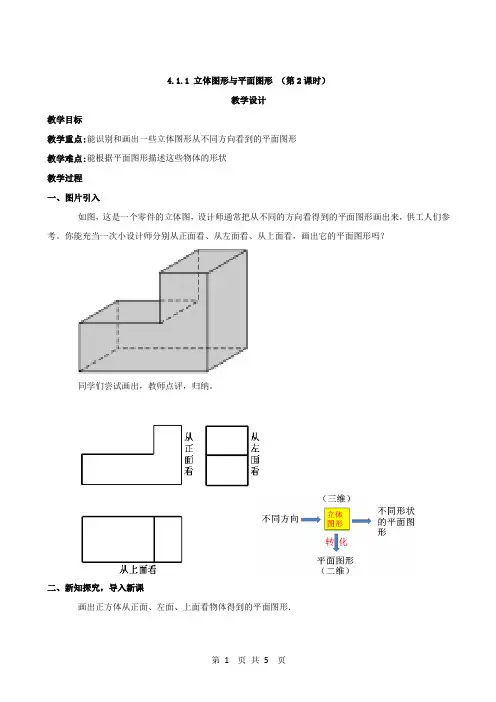
4.1.1 立体图形与平面图形(第2课时)教学设计教学目标教学重点:能识别和画出一些立体图形从不同方向看到的平面图形教学难点:能根据平面图形描述这些物体的形状教学过程一、图片引入如图,这是一个零件的立体图,设计师通常把从不同的方向看得到的平面图形画出来,供工人们参考。
你能充当一次小设计师分别从正面看、从左面看、从上面看,画出它的平面图形吗?同学们尝试画出,教师点评,归纳。
二、新知探究,导入新课画出正方体从正面、左面、上面看物体得到的平面图形.学生尝试画出来,教师点评,归纳,让孩子们初步了解三视图,为后续学习、研究立体几何做准备。
三、动手操作.探究新知活动:分别正面、左面、上面观察下面立体图形,看一看各能得到什么平面图形?同学们,自己动手画图,教师点评。
典例分析:例1 下图是一个由9个正方体组成的立体图形,分别从正面、左面、上面观察这个图形,各能得到什么平面图形?小试牛刀:1.从正面、左面、上面看立体图形各能得到什么平面图形?同学们尝试完成,教师点评。
例2 分别从正面、左面、上面看一个由若干个正方体组成的立体图形,得到的平面图形如下图所示,你能搭出这个立体图形吗?动手试试看!教师引导,和孩子们一块儿完成,总结。
2.由棱长为1的正方体搭成的积木,从三个方向看到的图形如下图所示,则棱长为1的正方体的个数是( c )A. 4B. 5C. 6D. 7四、当堂检测1. 观察下列立体图形,从正面看可得到平面图形_D__,从左面看是_C___,从上面看是_A___.2.下图所示的从正面、上面看到的图形对应哪个物体?( B ).3.下图是一块带有圆形空洞和方形空洞的工件,则下列物体中既可以堵住圆形空洞,又可以堵住方形空洞的是( B ).五、评价反思.概括总结这节课,同学们通过自己动手操作,自己发现,自己感知推导得到了从立体图形到平面图形,充分发挥了同学们的聪明才智,动手能力,大家交流合作得很愉快。
谈谈你有什么收获?立体图形三视图渗透的数学思想:转化.类比.抽象.概括。
4.1.1 立体图形与平面图形(1)教学设计刘官庄中学盛平梅教学内容:几何图形,立体图形和平面图形的概念,认识,辨别常见的几何图形。
教学目标1.理解几何图形的概念(问题1,2,3)立体图形和平面图形的概念,能区分立体图形和平面图形(问题4、问题5) 。
2. 能认识一些简单立体图形(问题6) ,能找出立体图形中的平面图形(问题7) 。
教学重点:几何图形、立体图形和平面图形的概念,常见几何图形的识别.教学难点:从实物原型中抽象出几何图形。
教学手段:多媒体课件、几何图形模型、卡纸等。
教学过程:一.创设情境,引入课题学生欣赏一组图片。
提出问题:问题1.你能从图片中找到哪些你熟悉的图形?学生观察,推荐几名学生描述自己的发现。
教师归纳点评。
问题2.你能从周围的事物中再举出一些常见的图形吗? 通过一个游戏来找一下(游戏:规则:给出不同物体名称,让一个同学根据它的形状说出与它有关的图形,同伴根据他的描述说出物体的名称。
•魔方铅笔乒乓球字典易拉罐•五星红旗三角板量角器教师归纳:通过刚才的游戏我们发现,物体的形状是物体的重要性质,也是几何中研究的内容。
这节课我们就来学习几何图形。
教师揭示课题,并板书课题。
二观察发现探索尝试问题3学生观察图片或实物,从中抽象几何图形。
学生先独立思考,再讨论交流, (学生完成导学案第1,2,3题)师生共同归纳:(1)、各种各样的物体除了具有颜色、材料、质量等性质外,还具有形状(如方的、圆的)、大小(如长度、面积、体积等)和位置(如平行、相交、垂直等),物体的形状、大小和位置关系是几何中研究的内容。
(2)长方体、圆柱、球、长(正)方形、圆、线段、点等,以及小学中学过的三角形、四边形等,都是从形形色色的物体外形中得出的,它们都是几何图形。
师参与学生讨论并引导,师生共同归纳几何图形的定义。
三动手操作,观察分析以小组为单位,将各种几何图形的实物或模型分为两类,并尝试说明分类的依据。
学生在组内讨论交流。
人教新版七年级上学期《4.1.1 立体图形与平面图形》同步练习卷一.选择题(共22小题)1.如图,这个立体图形中小正方体的个数是()A.9个B.10个C.11个D.12个2.如图的几何体由5个相同的小正方体搭成.从正面看,这个几何体的形状是()A.B.C.D.3.下列几何图中,是棱锥的是()A.B.C.D.4.下列几何体中,是圆锥的为()A.B.C.D.5.下列所述物体中,是球体的是()A.铅笔B.打足气的自行车内胎C.乒乓球D.电视机6.下面几何体中,既不是柱体,又不是锥体的是()A.B.C.D.7.下列几何体中,面的个数最少的是()A.B.C.D.8.如图所示的四种物体中,哪种物体最接近于圆柱()A.B.C.D.9.在一个正方体的玻璃容器内装了一些水,把容器按不同方式倾斜,容器内水面的形状不可能是以下哪些图形()A.锐角三角形B.钝角三角形C.等腰梯形D.五边形10.下列图形中,是棱柱的是()A.B.C.D.11.如图,一个有盖的圆柱形玻璃杯中装有半杯水,若任意放置这个水杯,则水面的形状不可能是()A.B.C.D.12.下列各组图形中都是平面图形的是()A.三角形、圆、球、圆锥B.点、线段、棱锥、棱柱C.角、三角形、正方形、圆D.点、角、线段、长方体13.下列图形中,含有曲面的立体图形是()A.B.C.D.14.不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征,甲同学:它有4个面是三角形;乙同学,它有6条棱,则该模型对应的立体图形可能是()A.三棱柱B.四棱柱C.三棱锥D.四棱锥15.下列图形属于棱柱的有()A.2个B.3个C.4个D.5个16.下列立体图形中,不属于多面体的是()A.四棱柱B.圆锥C.五棱柱D.长方体17.如图,下列图形全部属于柱体的是()A.B.C.D.18.下列几何体中,是柱体的是()A.B.C.D.19.把立方体的六个面分别涂上六种不同的颜色,并画出朵数不等的花,各面上的颜色与花朵的朵数情况列表如下:现将上述大小相同,颜色、花朵分布完全一样的四个立方体拼成一个水平放置的长方体,如图所示,那么长方体的表面包括下底面共有多少朵花朵.()A.60B.61C.62个D.63个20.下列各图是立体图形的是()A.B.C.D.21.下列几何体中,属于棱柱的有()A.3个B.4个C.5个D.6个22.下列说法中,不正确的是()A.棱柱的侧面可以是三角形B.棱柱的侧面展开图是一个长方形C.若一个棱柱的底面为5边形、则可知该棱柱侧面是由5个长方形组成的D.棱柱的上底面与下底面的形状与大小是完全一样的二.填空题(共8小题)23.一个棱柱共有21条棱,则这个棱柱共有个面.24.四棱柱有条侧棱.25.六棱柱有条棱,顶点,个面.26.六棱柱是一个立体图形,它是由个面,条棱,个顶点组成的.27.下面的几何体中,属于柱体的有个.28.正六棱柱有个顶点.29.若一个棱柱有7个面,则它是棱柱.30.如图,一个正方体的表面上分别写着连续的6个整数,且每两个相对面上的两个数的和都相等,则这6个整数的和为.三.解答题(共2小题)31.如图所示为8个立体图形.其中,柱体的序号为,锥体的序号为,有曲面的序号为.32.(1)下面这些基本图形和你很熟悉,试一试在括号里写出它们的名称.()()()()()(2)将这些几何体分类,并写出分类的理由.人教新版七年级上学期《4.1.1 立体图形与平面图形》2019年同步练习卷参考答案与试题解析一.选择题(共22小题)1.如图,这个立体图形中小正方体的个数是()A.9个B.10个C.11个D.12个【分析】按照每层的小正方体的个数,相加即可得到这个立体图形中小正方体的个数.【解答】解:由图可得,第一层有7个;第二层有5个;故这个立体图形中小正方体的个数是12个,故选:D.【点评】本题主要考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.2.如图的几何体由5个相同的小正方体搭成.从正面看,这个几何体的形状是()A.B.C.D.【分析】根据从正面看得到的图形是主视图,可得答案.【解答】解:从正面看第一层是三个小正方形,第二层中间一个小正方形,故选:A.【点评】本题考查了简单几何体的三视图,从正面看得到的图形是主视图.3.下列几何图中,是棱锥的是()A.B.C.D.【分析】根据棱锥的定义判断即可.【解答】解:A、是圆柱,B、是圆锥,C、是正方体,D、是三棱锥,故选:D.【点评】本题考查了认识立体几何,正确的认识几何体是解题的关键.4.下列几何体中,是圆锥的为()A.B.C.D.【分析】根据圆锥的定义解答.【解答】解:观察可知,C选项图形是圆锥.故选:C.【点评】本题考查了认识立体图形,熟悉常见的立体图形是解题的关键.5.下列所述物体中,是球体的是()A.铅笔B.打足气的自行车内胎C.乒乓球D.电视机【分析】结合实物进行解答.【解答】解:A、铅笔是圆柱体,故本选项错误;B、打足气的自行车内胎不是球体,故本选项错误;C、乒乓球是球体,故本选项正确;D、电视机不是球体,故本选项错误;故选:C.【点评】此题主要考查了认识立体图形,结合实物,认识常见的立体图形,如:长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等.6.下面几何体中,既不是柱体,又不是锥体的是()A.B.C.D.【分析】解这类题首先要明确柱体,椎体、球体的概念,然后根据图示进行解答.【解答】解:A、是三棱柱,是柱体,不符合题意;B、是圆柱,是柱体,不符合题意;C、是球,属球体,符号题意;D、是圆锥,是锥体,不符合题意;故选:C.【点评】本题考查了立体图形的定义,注意几何体的分类,一般分为柱体、锥体和球,注意球和圆的区别,球是立体图形,圆是平面图形.7.下列几何体中,面的个数最少的是()A.B.C.D.【分析】根据三棱柱、四棱柱、圆锥和圆柱的特点找到答案即可.【解答】解:三棱柱有5个面;长方体有6个面;圆锥有一个曲面和一个底面共2个面;圆柱有一个侧面和两个底面共3个面,面的个数最少的是圆锥,故选:C.【点评】考查了立体图形的概念,根据几何体直观的写出其所有的面是解答本题的关键,属于基础题,比较简单.8.如图所示的四种物体中,哪种物体最接近于圆柱()A.B.C.D.【分析】观察所给图形,根据圆柱体的特点即可做出判断.【解答】解:最接近圆柱的是生日蛋糕.故选:A.【点评】本题考查了认识立体图形,比较简单,熟悉圆柱体是解题的关键.9.在一个正方体的玻璃容器内装了一些水,把容器按不同方式倾斜,容器内水面的形状不可能是以下哪些图形()A.锐角三角形B.钝角三角形C.等腰梯形D.五边形【分析】根据正方体的截面性质判断即可.【解答】解:在一个正方体的玻璃容器内装了一些水,把容器按不同方式倾斜,容器内水面的形状不可能是钝角三角形,故选:B.【点评】此题考查了认识立体图形,弄清正方体截面的特征是解本题的关键.10.下列图形中,是棱柱的是()A.B.C.D.【分析】根据棱柱与棱锥的区别进行判断.【解答】解:A、是三棱锥,故A错误;B、是圆柱,故B错误;C、是圆锥,故C错误;D、是三棱柱,故D正确;故选:D.【点评】本题考查了认识立体图形:结合实物,认识常见的立体图形,如:长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等.11.如图,一个有盖的圆柱形玻璃杯中装有半杯水,若任意放置这个水杯,则水面的形状不可能是()A.B.C.D.【分析】根据圆柱体的截面图形可得.【解答】解:将这杯水斜着放可得到A选项的形状,将水杯倒着放可得到B选项的形状,将水杯正着放可得到D选项的形状,不能得到三角形的形状,故选:C.【点评】本题主要考查认识几何体,解题的关键是掌握圆柱体的截面形状.12.下列各组图形中都是平面图形的是()A.三角形、圆、球、圆锥B.点、线段、棱锥、棱柱C.角、三角形、正方形、圆D.点、角、线段、长方体【分析】根据平面图形定义:一个图形的各部分都在同一个平面内的图形是平面图形可得答案.【解答】解:A、球、圆锥是立体图形,错误;B、棱锥、棱柱是立体图形,错误;C、角、三角形、正方形、圆是平面图形,正确;D、长方体是立体图形,错误;故选:C.【点评】此题主要考查了平面图形,关键是掌握平面图形的定义.13.下列图形中,含有曲面的立体图形是()A.B.C.D.【分析】根据立体图形的特征,可得答案.【解答】解:A、角是平面图形,故A不符合题意;B、半圆环是平面图形,故B不符合题意;C、棱台不含曲面,故C不符合题意;D、侧面是曲面的立体图形,故D符合题意;故选:D.【点评】本题考查了认识立体图形,正确区分平面图形与立体图形是解题关键.14.不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征,甲同学:它有4个面是三角形;乙同学,它有6条棱,则该模型对应的立体图形可能是()A.三棱柱B.四棱柱C.三棱锥D.四棱锥【分析】根据三棱锥的特点,可得答案.【解答】解:侧面是三角形,说明它是棱锥,底面是三角形,说明它是三棱锥,故选:C.【点评】本题考查了认识立体图形,熟记常见几何体的特征是解题关键.15.下列图形属于棱柱的有()A.2个B.3个C.4个D.5个【分析】根据棱柱的概念、结合图形解得即可.【解答】解:第一、二、四个几何体是棱柱,故选:B.【点评】本题考查的是立体图形的认识,认识常见的立体图形,如:长方体、正方体、圆柱、圆锥、球、棱柱、棱锥是解题的关键.16.下列立体图形中,不属于多面体的是()A.四棱柱B.圆锥C.五棱柱D.长方体【分析】根据由多个平面组成的几何体是多面体,可得答案.【解答】解:∵圆锥是旋转体,四棱柱、长方体、五棱柱都是多面体,∴圆锥不是多面体,故选:B.【点评】本题考查了认识立体图形,多面体是由多个平面组成的几何体,注意圆锥是旋转体.17.如图,下列图形全部属于柱体的是()A.B.C.D.【分析】根据柱体的定义,结合图形即可作出判断.【解答】解:A、左边的图形属于锥体,故本选项错误;B、上面的图形是圆锥,属于锥体,故本选项错误;C、三个图形都属于柱体,故本选项正确;D、上面的图形不属于柱体,故本选项错误.故选:C.【点评】此题考查了认识立体图形的知识,属于基础题,解答本题的关键是掌握柱体和锥体的定义和特点,难度一般.18.下列几何体中,是柱体的是()A.B.C.D.【分析】根据柱体的概念和定义即可解.【解答】解:A、该图形是圆锥体,故本选项错误;B、该图形是三棱锥,故本选项错误;C、该图形上下两底面不全等,不是柱体,故本选项错误;D、该图形是正方体,属于柱体,故本选项正确.故选:D.【点评】本题考查的棱柱的定义,关键点在于:棱柱的侧面是几个长方形围成,且上下底面是相等的.19.把立方体的六个面分别涂上六种不同的颜色,并画出朵数不等的花,各面上的颜色与花朵的朵数情况列表如下:现将上述大小相同,颜色、花朵分布完全一样的四个立方体拼成一个水平放置的长方体,如图所示,那么长方体的表面包括下底面共有多少朵花朵.()A.60B.61C.62个D.63个【分析】先根据图形得出最右边的正方体是:上蓝,下白,左绿,右红,前黄,后紫,即可推出其它正方形,代入朵数即可得出答案.【解答】解:∵大小颜色花朵分布完全一样,∴最左边的正方体告诉我们:黄色紧邻的面是白色;最右边的正方体告诉我们:黄色紧邻着红色和蓝色;∴可以推断出最右边的正方体的白色面是在它的左侧面或下底面;又∵右数第二个正方体告诉我们红色紧邻着白色;∴对于最右边的正方体,白色只可能在下底面(如果在左侧面就与红色是对立面了,不符题意);∵根据左数第二个正方体可知:红色紧邻着紫色;∴对于最右边的正方体,后侧面是紫色,左侧面是绿色.即最右边的正方体为例,它是:上蓝,下白,左绿,右红,前黄,后紫.也就是说:黄的对立面是紫;紫的对立面是黄;红的对立面是绿,蓝的对立面是白.依次对应从左至右的四个正方体,下底面分别是:紫,黄,绿,白.∴长方体的上面有花:2+5+1+3=11朵,前面有花:4+1+4+2=11朵,下面有花:5+2+6+4=17朵,后面有花:3+6+3+5=17朵,左面有花:1朵,右面有花:6朵,长方体的表面包括下底面共有:11+11+17+17+6+1=63朵.故选:D.【点评】考查了认识立体图形,注意正方体的空间图形,从相对面入手,分析及解答问题.20.下列各图是立体图形的是()A.B.C.D.【分析】根据立体图形的定义,可得答案.【解答】解:由题意,得三棱锥是立体图形,故选:D.【点评】本题考查了立体图形,每个面不在同一个平面内是解题关键.21.下列几何体中,属于棱柱的有()A.3个B.4个C.5个D.6个【分析】根据棱柱的概念、结合图形解得即可.【解答】解:第一、第三、第六个几何体是棱柱,共有3个.故选:A.【点评】本题考查的是立体图形的认识,认识常见的立体图形,如:长方体、正方体、圆柱、圆锥、球、棱柱、棱锥是解题的关键.22.下列说法中,不正确的是()A.棱柱的侧面可以是三角形B.棱柱的侧面展开图是一个长方形C.若一个棱柱的底面为5边形、则可知该棱柱侧面是由5个长方形组成的D.棱柱的上底面与下底面的形状与大小是完全一样的【分析】根据棱柱的结构特征进行判断.【解答】解:A、棱柱的每一个侧面都是平行四边形,故本选项错误;B、棱柱的侧面展开图是长方形,故本选项正确;C、一个棱柱的底面是一个5边形,则它的侧面必须有5个长方形组成,故本选项正确;D、棱柱的上下底面是全等的多边形,则棱柱的上下底面是形状、大小相同的多边形.故本选项正确;故选:A.【点评】本题考查了立体图形的认识,熟记常见立体图形的结构特征是解题的关键.二.填空题(共8小题)23.一个棱柱共有21条棱,则这个棱柱共有9个面.【分析】根据棱柱的概念和定义,可知有21条棱的棱柱是七棱柱.【解答】解:21÷3=7,∴一个棱柱共有21条棱,那么它是七棱柱,∴这个棱柱共有9个面.故答案为:9.【点评】本题主要考查了认识立体图形,解决问题的关键是掌握棱柱的结构特征.24.四棱柱有4条侧棱.【分析】根据立体图形,即可解答.【解答】解:四棱柱有4条侧棱,故答案为:4.【点评】本题考查了棱柱的特征,解题时可以运用一般规律:n棱柱有(n+2)个面,2n 个顶点和3n条棱.25.六棱柱有18条棱,12顶点,8个面.【分析】根据六棱柱的概念和定义即可得出答案.【解答】解:因为六棱柱上下两个底面是6边形,侧面是6个长方形,所以共有12个顶点;8个面;18条棱.故答案为18,12,8.【点评】此题主要考查了立体图形,解决本题的关键是掌握六棱柱的构造特点.26.六棱柱是一个立体图形,它是由8个面,18条棱,12个顶点组成的.【分析】根据长方体的特征,六棱柱有8个面,相对的面面积相等;有18条棱互相平行的一组4条棱的长度相等;有12个顶点.【解答】解:六棱柱有8个面,18条棱,12个顶点.故答案为:8,18,12.【点评】此题主要考查认识立体图形的知识,解题的关键是了解长方体的特征.27.下面的几何体中,属于柱体的有4个.【分析】解这类题首先要明确柱体,椎体、球体的概念,然后根据图示进行解答.【解答】解:柱体分为圆柱和棱柱,所以柱体有圆柱、正方体、六棱柱,三棱柱共4个.故答案为:4.【点评】本题考查了立体图形的定义,注意几何体的分类,一般分为柱体、锥体和球,注意球和圆的区别,球是立体图形,圆是平面图形.28.正六棱柱有12个顶点.【分析】根据正六棱柱上、下地面各有6个顶点,据此可得.【解答】解:正六棱柱有12个顶点.故答案为:12.【点评】本题主要考查认识立体图形,解题的关键是掌握常见几何体的形状和构成.29.若一个棱柱有7个面,则它是5棱柱.【分析】根据棱柱有两个底面求出侧面的面数,然后解答解答.【解答】解:∵棱柱有七个面,∴它有5个侧面,∴它是5棱柱,故答案为:5【点评】本题考查了认识立体图形,关键在于根据棱柱有两个底面确定出侧面的面数.30.如图,一个正方体的表面上分别写着连续的6个整数,且每两个相对面上的两个数的和都相等,则这6个整数的和为51.【分析】根据正方体的表面展开图,相对的面之间一定相隔一个正方形,判断出6是最小的数,然后确定出这六个数,再相加即可得解.【解答】解:∵正方体的表面展开图,相对的面之间一定相隔一个正方形,∴6若不是最小的数,则6与9是相对面,∵6与9相邻,∴6是最小的数,∴这6个整数的和为:6+7+8+9+10+11=51.故答案为:51.【点评】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.三.解答题(共2小题)31.如图所示为8个立体图形.其中,柱体的序号为①②⑤⑦⑧,锥体的序号为④⑥,有曲面的序号为③④⑧.【分析】根据柱体的意义,椎体的意义,可得答案.【解答】解:柱体的序号为①②⑤⑦⑧,锥体的序号为④⑥,有曲面的序号为③④⑧,故答案为:①②⑤⑦⑧;④⑥;③④⑧.【点评】本题考查了认识立体图形,正确区分柱体和锥体是解题关键.32.(1)下面这些基本图形和你很熟悉,试一试在括号里写出它们的名称.()()()()()(2)将这些几何体分类,并写出分类的理由.【分析】(1)针对立体图形的特征,直接填写它们的名称即可.(2)可以按柱体、锥体和球进行分类,也可以按平面和曲面进行分类,方法不同,答案不同,只要合理即可.【解答】解:(1)从左向右依次是:球、圆柱、圆锥、长方体、三棱柱.(2)观察图形,按柱、锥、球划分,则有圆柱、长方体、三棱柱为柱体;圆锥为锥体;球为球体.【点评】本题考查了立体图形的认识和几何体的分类.熟记常见立体图形的特征是解决此类问题的关键.几何体的分类,从图形形状可以分为柱体、锥体和球三种,注意结合实际几何体的特征进行分类.。