当前位置：文档之家 › 相量法

相量法

  • 格式：ppt
  • 大小：987.50 KB
  • 文档页数：30

下载文档原格式

  / 30

合集下载

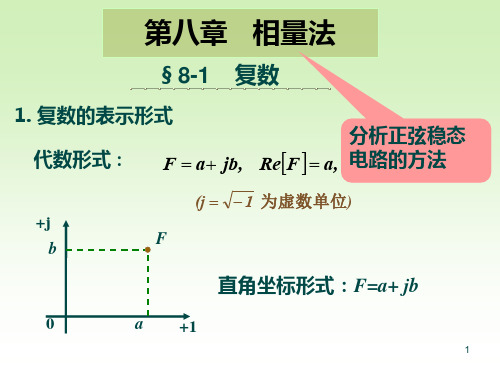
第八章相量法

第八章相量法

结论 任意一个正弦时间函数都有唯
一与其对应的复数函数。 一与其对应的复数函数。
i = 2 Icos( ωt + ϕ ) ↔ F ( t ) = 2 Ie
j ( ω t +ϕ )
17
§8-3 相量法的基础
i = 2 Icos( ωt + ϕ ) ↔ F ( t ) = 2 Ie
F(t)还可以写成 F ( t ) = 还可以写成
1 I= T
def
∫
∫
T
0
i 2 ( t )dt
可定义电压有效值： 可定义电压有效值： 电压有效值
1 U= T
def T 0
u 2 ( t )dt
13
§ 8-2
正弦量
正弦电流、 正弦电流、电压的有效值
设正弦电流 i = I m cos(ω t + φi )
1 T 2 I= I m cos 2 (ω t + φi ) dt T ∫0 = 1 I m = 0.707 I m 2
ejπ/2 =j , e-j π /2 = -j, 可以看成旋转因子。 可以看成旋转因子。
ejπ= –1 故 +j, –j, -1 都 1 j,
4
§ 8-2
1.正弦量： 正弦量： 正弦量
i + u _
正弦量
i
0
T
ωt
波形
瞬时值表达式
i(t) = I m cos( ω t + φi )
周期T 和频率f 周期 和频率
i、 I m 、 I ；
u、U m 、U
14
i = I m cos(ω t + φi ) = 2 Icos(ω t + φi ) u = U m cos(ω t + φu ) = 2U cos(ω t + φu )

相量法的运算公式

相量法的运算公式

相量法的运算公式
相量的运算公式包括：
1.相量的加减法：
a+b = (a_x + b_x) + (a_y + b_y) j
a-b = (a_x - b_x) + (a_y - b_y) j
其中，a_x和a_y分别为向量a在x轴和y轴上的分量，b_x和b_y分别为向量b在x轴和y轴上的分量，j为虚数单位。

2.相量的乘法：
a*b = (a_magnitude * b_magnitude) * exp(j * (a_angle +
b_angle))
其中，a_magnitude和b_magnitude分别为向量a和b的模长，a_angle和b_angle分别为向量a和b与实部轴之间的夹角，exp为指数函数，j为虚数单位。

相量法拓展：
1.相量法不仅适用于平面向量，在空间向量中同样适用，只是需要增加z轴分量。

2.相量法不仅适用于电学领域中的交流电路分析，还适用于机械学、热力学的分析，以及计算机图形学中的向量运算等领域。

3.利用相量法，可以求解平面图形的面积、角度、垂直平分线、内心、外心等问题。

相量法

相量法

ω = 0(直流), X L = 0, 短路 ; ; ω → ∞, X L → ∞, 开路
ω
相量表达式: 相量表达式
& & & U = jX L I = jωLI ,
& = jB U = j − 1 U = 1 U & & & I L jωL ωL
返 回 上 页 下 页
波形图及相量图： 波形图及相量图：
返 回 上 页 下 页
电感元件VCR的相量形式 2. 电感元件 的相量形式
时域形式： 时域形式：
已知 i(t ) = 2I cos(ω t +ψi )
i(t) + uL(t) •
则
L
di(t ) uL (t ) = L = − 2ωL I sin(ω t +Ψ ) i dt π = 2ω L I cos(ω t +Ψ + ) i 2
uL O
pL i
2π π
& UL
电压超前电 流900
& I
ωt
Ψi
功率： 功率：
pL = uLi = ULm Im cos(ωt +Ψ ) sin(ω t +Ψ ) i i = UL I sin 2(ω t +Ψ ) i
瞬时功率以2ω交变，有正有负，一周期内刚好互相抵消 瞬时功率以 ω交变，有正有负，
返 回 上 页 下 页
波形图及相量图： 波形图及相量图： pR uR i
& UR
URI
& I
Ψu=Ψi
同 相 位
O
ωt
瞬时功率： 瞬时功率：
pR = uRi = 2UR 2I cos2 (ω t +Ψ i )

第八章 相量法

第八章 相量法

w 2 f 2 T
单位： rad/s ，弧度 / 秒 i Im O T 2
(3) 初相位(initial phase angle) i 反映正弦量的计时起点。
/w i
twt
同一个正弦量，计时起点不同，初相位不同。
i
一般规定：| | 。
O
t
=0 =－/2
二. 相位差 ：
T
0
1 cos 2(w t i ) 1 dt t 2 2
T 0
1 T 2
1 2 T Im I Im 0.707 I m T 2 2
i(t ) I m cos(w t i ) 2I cos(w t i )
Im 2I
同理，可得正弦电压有效值与最大值的关系：
u( t ) u1 ( t ) u2 ( t ) Re( 2 U 1 e Re( 2 U 1 e
可得其相量关系为：



jwt
) Re( 2 U 2 e jwt )


jwt
2U2 e

jwt
) Re( 2 (U 1 U 2 )e jwt )
U U1 U 2
相量的模表示正弦量的有效值
相量的幅角表示正弦量的初相位
同样可以建立正弦电压与相量的对应关系：
u( t ) 2U cos(w t θ ) U Uθ
例1 已知
i 141.4 cos(314t 30o )A u 311.1cos(314t 60o )V
试用相量表示i, u .
e cos j sin
指数形式
F=|F|（cos + jsin ）

相量法专业知识讲座

相量法专业知识讲座

同理，可得正弦电压有效值与最大值旳关系：
U
1 2 Um
或
U m 2U
若一交流电压有效值为U=220V，则其最大值为Um311V；
U=380V，
Um537V。
工程上说旳正弦电压、电流一般指有效值，如设备铭牌 额定值、电网旳电压等级等。但绝缘水平、耐压值指旳是 最大值。所以，在考虑电器设备旳耐压水平时应按最大值 考虑。
强制分量(特解)：Imcos(w t+ i)
Um cos(wt u ) RIm cos(wt i ) wLIm cos(wt i ) Im R2 (wL)2 cos(wt i θ)
O
O
t
2. 相量运算
(1) 同频率正弦量相加减
u1(t )
2 U1 cos(wt 1) Re(
2
•
U
1
e
jwt
)
u2 (t )
2 U2 cos(wt 2) Re(
2
•
U
2
e
jwt
)
u(t ) u1(t ) u2 (t ) Re(
2
•
U
1
e
jwt
)
Re(
2
•
U
2
e
jwt
)
Re(
而幅角与t成正比，可视其为一旋转相量，当t从0~T时，
相量旋转一周回到初始位置， w t 从0~2。
•
2 I e jwt 2Ie j e jwt 2Ie j(wt )是模为 2I , 初始角度
为 的旋转相量,其旋转一周在实轴上的 投影即为正弦 电流 i 2 I cos(wt )。
+1
i
w
φ +j 2I

电路分析相量法

电路分析相量法

量的相量乘以 jω ，即表示di/dt 的相量为
j I I( i 90o )
该相量的模为ωI ，辐角则超前原相量π/2 。
对 i 的高阶导数 dni/dtn ，其相量为 ( j )。n I
3)正弦量的积分
设 i 2I cos( t i )，则
idt Re[ 2Ie j t ] dt Re[ (
F1F2 | F1 | 1 | F2 | 2 | F1 || F2 | (1 2 )
可见复数的乘法运算使用指数形式或极坐标形式较为简便。
3)除法运算
a)代数形式
F1 F2
a1 a2
jb1 jb2
(a1 (a2
jb1 )(a2 jb2 )(a2
jb2 ) jb2 )
(a1a2
b1b2 ) j(a2b1 a22 b22
设 F1 a1 jb1 ， F2 a2 jb2 ，则
F1 F2 (a1 jb1 ) (a2 jb2 ) (a1 a2 ) j(b1 b2 )
平行四边形法则：
+j F1 +F2 F1
F2 o
+1
+j F1
F2 o
F1－F2 +1
2)乘法运算 a)代数形式
F1F2 (a1 jb1 )(a2 jb2 ) (a1a2 b1b2 ) j(a1b2 a2b1 )
di d Re[ 2Ie j t ] Re[ d ( 2Ie j t )] Re[ 2( j I)e j t ]
dt dt
dt
Re[ 2 Ie ] j( ti 90o ) 2 I cos( t i 90o )
上式表明：
复指数函数实部的导数等于复指数函数导数的实部；

第八章相量法

i i
i
i
i
如 i 26 2 cos(t 60) A 26e j 60 A 2660 A I 对应的有效值相量为：
Im 26 2e j 60 A 26 260 A 其最大值相量为：
U 同理若有： 220e j 30V 则有; u 220 2 cos(t 30)V 2.相量图 相量是一个复数，它在复平面上的图形称为相量图。 若用旋转相量表示为，2Ie j e jt 其中复常数 2Ie j 2I i 称为旋转相量的复振幅， e jt 是一个随时间变化而以角速度不断逆时针旋转 的因子，两者的乘积即表示复振幅在复平面上不断 逆时针旋转，故称之为旋转相量，这就是复指数 函数的几何意义。
dt 2
③正弦量的积分
i 2I cos(t i ) 则 idt Re [ 2 Ie jt ]dt Re [ 2 Ie jt dt ] 如
jt I I Re [ 2 ( )e ] 2 cos(t i ) j 2
即正弦量的积分为同频率正弦量，其相量等于原 j 相量 I 除以 . I I 表示为： ( i ) idt
F F1 F2 F1 F2 [cos( 1 2 ) j sin(1 2 )]
F1 a1 jb1 (a1 jb1 )(a2 jb2 ) a1a2 b1b2 a2 b1 a1b2 j 2 2 2 2 F2 a2 jb2 (a2 jb2 )(a2 jb2 ) a2 b2 a2 b2
1
i1 I1m cos(t i 1 ) A 和 i2 I 2 m cos(t i 2 ) A 则 i1 与 i 2 如 的相位差 12 (t i1 ) (t i 2 ) i1 i 2 （初相之差）

相量法

+j F1 0 F = F1 + F2 F2 +1
复数的乘除运算 a. 复数的乘除运算可以用代数形式进行 例如：设F1 =a1+jb1, F2 =a2+jb2, 则
F1F2 (a1 jb1 )(a2 jb2 ) (a1a2 - b1b2 ) j(a1b2 a2b1 )
F1 a1 jb1 (a1 jb1 )(a2 - jb2 ) F2 a2 jb2 (a2 jb2 )(a2 - jb2 )
a1a2 b1b2 a2b1 - a1b2 j 2 2 (a2 ) (b2 ) (a2 )2 (b2 )2
b. 复数的乘除运算也可以用指数形式和极坐标进行（方便）
两个复数的相乘，用指数形式进行, 有
F1F2 F1 e
用极坐标形式表示, 有
j1
F2 e
j 2
F1 F2 e
3. 相量图 相量图: 相量是一个复数，它在复平面上的图形称为相量图。
I i (t ) 2 Icos(ω t i ) I i
U u(t ) 2Ucos(t u ) U u
U

u
i
I

4. 正弦量运算转换为相应相量运算 (1) 同频率正弦量的代数和
2 倍的关系。
工程中一般说正弦电压、电流的大小都指有效值。如测量 仪表上的刻度，设备名牌上的额定电压、电流均指有效值。 但电器设备的绝缘水平 — 耐压值按最大值考虑。
§8. 3相量法的基础
1. 相量法的理论基础 从电路分析中常涉及到的计算看：有正弦量乘常数（欧姆定 律），正弦量的微分、积分（电感、电容电路的电压电流约 束关系），同频率正弦量的代数和（KCL和KVL）等运算， 其结果仍是一个同频率的正弦量。 在线性电路中，若激励是正弦量，则电路中各支路的电压和 电流的稳态响应将是同频率的正弦量；若电路中有多个同频 率激励源时，根据线性电路的叠加定理，则电路的全部稳态 响应都将是同频率的正弦量 — 这是一个基本的结果。 基于以上原因，在同频正弦量的电路计算中，ω是已知 的常 数，正弦量的三要素已退化成两个要素，有效值（最大值） 和初相，注意到一个复数（相量）也有两个要素：模和辐角， 这使得可用复数表征一个正弦量的信息（要素）。 电工技术中的非正弦周期函数，可以分解成频率为整数倍的 正弦函数的无穷级数，最终归结为这里讨论的正弦稳态分析。

电路相量法

电路相量法相量法是分析讨论正弦电流电路稳定状态的一种简洁易行的方法。

它是在数学理论和电路理论的基础上建立起来的一种系统方法。

1、问题的提出在上图所示的电路中，依据KVL，列写微分方程如下当激励u(t)是正弦量时，uC(t)及iL(t)均为同频率的正弦量。

这一重要结论具有普遍意义，即线性非时变电路在正弦电源激励下，各支路电压、电流的特解都是与激励同频率的正弦量，当电路中存在有多个同频率的正弦激励时，该结论也成立。

工程上将电路的这一特解状态称为正弦电流电路的稳定状态，简称正弦稳态。

电路处于正弦稳态时，同频率的各正弦量之间仅在有效值（或幅值）、初相上存在差异和联系，这种"差异和联系"正是正弦稳态分析求解中的关键问题。

结论：同频的正弦量相加仍得到同频的正弦量，所以，只需确定初相位和有效值。

因此采纳2、正弦量的相量表示：构造一个复函数，（无任何物理意义）取该复函数的实部，，为一个正弦量，有物理意义。

结论：任意一个正弦时间函数都有唯一与其对应的复数函数。

如复函数F(t) 还可以写成，其中为复常数。

F(t) 包含了正弦量的三要素：幅值（此处为有效值）I、初相Y 、角频率w。

有如下关系同样可以建立正弦电压与相量的对应关系：正弦量除可用上述的相量式表示以外，还可在复平面上用相量图形式表示。

如图所示。

图相量图留意相量的模表示正弦量的有效值；相量的辐角表示正弦量的初相位。

例已知，试用相量表示i和u。

解：3、相量法的应用① 同频率正弦量的加减所以相量关系为：结论：同频正弦量的加减运算变为对应相量的加减运算。

同频率的正弦量相加减，还可以借助相量图进行计算。

令，，下面用相量图求解。

图(a)为平行四边形法则求解，图(b)为三角形法则求解。

(a) (b)图相量图进行相量的加法运算② 正弦量的微分、积分运算令微分运算：积分运算：所以；相量法的优点：① 把时域问题变为复数问题；② 把微积分方程的运算变为复数方程运算；③ 可以把直流电路的分析方法直接用于沟通电路。

第八章 相量法

而A2中包含了正弦量中不同变量中可变的两个要素I、φ i （不同变量，I、φ i 不相同）。 定义：1：A1 2e jt 称为旋转矢量——是个不变的复指数函数
可以看出 i(t)和指数函数A是一一对应的关系，再将A作如下变换：
其在实轴上的投影随时间规律变化就是正弦量（取实部）。
2e jt 是随时间从实轴出发沿逆时针方向旋转的一个矢量，
而 i(t ) Re[I 2e jt ]






I I1 I 2
2. 相量的乘除 u (t ) 2U cos(t u ) U U u i (t ) 2 I cos(t ) I I
i i
复阻抗
U U u U Z ( u i ) I i I I Z z

I 1 I 1 1 I 2 I 2 2 I I I
1 2
显然，三角函数本身的代数和较 麻烦，若转化为相量求代数和后 再转换成正弦函数就容易的多。
i(t ) i1 (t ) i2 (t ) Re I1 2e jt Re I 2 2e jt Re (I1 I 2 ) 2e jt
U Z I Z z Ii Uu
3．正弦量的一阶微分（积分）仍为同频率的正弦量，其相量为原正弦量的相 量乘以（除以） jω 。（P211） 正弦量的积分仍为同频率的正弦量，其相量为原正弦量的相量除以jω 。
i (t ) 2 I cos(t i ) 则 di(t ) dt j I
除法时，复数的模直接相除，而幅角相减。
A1 1 A2 2 A1 A2 1 2
1 2
§8-2正弦量
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
15
1.正弦量的相量表示 设正弦电流 i 2 I cos(wt y i ) 复常数 构造复指数函数： F (t ) 2 Ie j(wt y i ) 2 Ie jy i e jwt +j 2Icos(wt y i ) j 2Isin( wt y i ) w
wt
Im
yi
O
+1
( 2) i1 ( t ) 10 cos(100 t 300 ) i2 ( t ) 10 sin(100 t 150 )
i2 (t ) 10 cos(100t 1050 )
j 300 (105 0 ) 135 0
i2 (t ) 3 cos( 100 t 150 0 )
e jwt ) Re( 2U e jwt ) u u1 u2 Re( 2U 1 2 e jwt 2U e jwt ) Re( 2 (U U )e jwt ) Re( 2U 1 2 1 2
U U U 1 2
相量加减运算：用代数式计算。
F1 F2 1 2
F1 F2 F1 e j1 F2 e j 2 F1 F2 e j(1 2 )
模相乘 角相加
F1 | F1 | θ1 | F1 | e jθ1 | F1 | j( θ1θ2 ) e jθ 2 F2 | F2 | θ2 | F2 | e | F2 | |F1| θ1 θ2 |F2|
Im I ，I m 2 I 2
13
同理，正弦电压有效值与最大值的关系：
Um U ，U m 2U 2
正弦电流、电压也可以表示为：
i 2I cos(wt y i )，u 2U cos(wt y u )
若交流电压有效值为：U=220V ， U=380V 其最大值为：Um311V Um537V 工程上正弦电压、电流一般指有效值，如设备的铭
j 300 (150 0 ) 120 0
(3) i1 (t ) 5 cos(100 t 30 )
0
i2 (t ) 3 cos(100 t 30 )
0
两个正弦量进行相位比较时应满足：同频率、同函
数、同符号，且在主值范围内比较。
11
4.有效值
1）有效值定义 物 理 意 义
试写出电流的瞬时值表达式。 解
i 50 2cos(314t 15 ) A

18
2.相量图
在复平面上用有向线段表示相量的图称为相量图。
Iy i 2I cos(ωt y i ) I i
Uy u 2U cos(wt y u ) U u
相量图可以直观地表示出 各个正弦量有效值和初相位
3
2.复数运算 ①加减运算 —— 采用代数式 若 F1=a1+jb1， F2=a2+jb2 则 F1±F2=(a1±a2)+j(b1±b2)
Im F2
F1+F2
Im
F1+F2
F2
F1 o 图解法 Re o
F1 Re
F2 F1-F2
4
②乘除运算 —— 采用极坐标式 若 F1=|F1| 则:
1 ，F2=|F2| 2
yu yi j 2）j <0， u滞后i |j | 角。
wt
正弦量之间的相位差不随计时起点的变化而变化。
9
特殊相位关系：
j 0， 同相：
u, i
u i
j = ，反相：
u, i u iw t
0
wt
u, i u i 0
0
j =/2，正交:
wt
10
例
计算下列两正弦量的相位差。
(1) i1 ( t ) 10 cos(100 t 3 4) j 3 4 ( 2) 5 4 0 i2 ( t ) 10 cos( 100 t 2) j 5 4 2 3 4
1 U U jwLI I jwL
U=wLI
I
相量模型
yi
yu=yi +90°
24
4.电容元件VCR的相量形式
i + u -
I
+ U -
已知 u 2U cos(wt y u ) du 则iC 2wCU sin( wt y u ) dt C 2wCU cos(wt y u 90 ) y 90 Iy I wCU u 相量形式 U
减运算。因此在正弦稳态电路中，KCL和KVL可以 用相量形式表示。
KCL：
KVL：
i(t ) 0 u(t ) 0
I 0 U 0
表明 流入任一结点的所有支路电流用相量表示
时仍满足KCL；而任一回路所有支路电压用相量表
示时仍满足KVL。
22
2.电阻元件VCR的相量形式 i 时域形式 R
U
同频正弦量的加减运算变成对应相量的加减运算。
20
2）正弦量的微分、积分运算
Iy i 2 I cos(wt y i ) I i
微分运算:
di d e jw t Re 2 I dt dt j w e jw t Re 2 I
积分运算:


e jw t dt i d t Re 2 I
F | F | e | F |
j
极坐标式
2
几种表示法的关系：
Im
F a jb
F | F | e | F |
j
b
|F|
F

o a Re
| F | a 2 b 2 b θ arctan a
或
a | F | cos b | F | sin
牌额定值、电网电压等级及交流测量仪表的读数等。
但绝缘水平、耐压值指的是最大值。
14
§8-3 相量法的基础
由于正弦稳态电路中同频率正弦量的加、减、微 分、积分运算后仍是同频率的正弦量，因此求解正 弦稳态电路时只需求出有效值和初相位。 相量法的思想：复数变换
正弦量 (三角函数)
正弦量运算 （三角函数运算） 待求正弦量 反变换 复数变换 相量 （复数） 相量运算 (复数运算) 相量结果
Iy i(t ) 2I cos(wt y i ) I i
模：表示正弦量的有效值； 辐角：表示正弦量的初相位。 同样可以建立正弦电压与相量的对应关系：
Uy u(t ) 2U cos(wt y u ) U u
I y ，U U y 最大值相量： I m m i m m u
时域形式
u
1 jωC
相量关系
I
U u滞后i 90°
1 I jwCU U I jwC
I=w CU yi=yu+90°
25
相量模型
yu
5.受控源VCR的相量形式 在正弦稳态电路中，受控源的电压或电流与控制 电压或电流是同频率的正弦量。因此受控源的VCR 也可以用相量形式表示。
Im
U

之间的关系。
注意：只有同频率的正弦 量才能画在同一相量图中。
yu yi
I
Re
19

3.相量的运算 1）正弦量的加、减运算
e jw t ) u1 2U1 cos(wt y 1 ) Re( 2U 1 e jw t ) u 2 U cos(wt §8-1 复数
• §8-2
• §8-3
正弦量
相量法的基础
• §8-4
电路定理的相量形式
1
§8-1 复数
1.复数的表示形式 Im b 代数式 |F| F
F a jb
(j 1 为虚数单位)

o a Re 三角函数式
F | F | e
j
指数式
F | F | e j | F | (cos j sin ) a jb
模相除 角相减
5
③旋转因子 复数 ej =1∠
Im
F• ej
F• ej
旋转因子
特殊旋转因子： 0

Im
F Re
jF
e j
j
π 2
F
Re
jF
6
e
j

2
j
0
e
j
1
F
§8-2 正弦量
正弦电流电路：正弦电源激励下的线性电路，其 稳态响应都是与激励同频率的正弦电压或电流（正 弦量），又称为正弦稳态电路。 正弦稳态电路在电力系统和电子技术领域占有十 分重要的地位。这是由于正弦电路有如下优点： 1）正弦信号易于产生、传送和使用，其加、减、 微分、积分运算后仍是同频率的正弦信号；
y =-/2
y
y =0
y =/2
1）振幅（最大值）：Im
峰－峰值： imax-imin=2Im
相位：w t+y 单位：rad/s(弧度/秒)
主值范围：|y|
8
同一个正弦量，计时起点不同，初相位也不同。
3.相位差
设 u(t)=Umcos(wt+yu), i(t)=Imcos(wt+yi)，则 相位差 ：j =(wt+yu)-(wt+yi)=yu-yi 1）j >0， u超前i j 角； u, i u o i |j |
Re[ F (t )] 2Icos(wt y i ) i
Imcos(wt+yi)
i(t ) F (t ) 一一对应 jy i i(t ) I Ie Iy
i
旋转矢量
正弦量对应的相量
F(t)包含了三个要素：I、yi 、w；相量包含了两 个要素：I , yi 。