第九章 计算分析题
- 格式:doc
- 大小:32.00 KB
- 文档页数:2

第九章期权估价一、单项选择题1.如果其他因素不变,下列有关影响期权价值的因素表述不正确的是()。
A.随着股票价格的上升,看涨期权的价值增加,看跌期权的价值下降B.看涨期权的执行价格越高,其价值越小,看跌期权的执行价格越高,其价值越大C.股价的波动率增加会使期权价值增加D.看涨期权价值与预期红利大小成正向变动,而看跌期权与预期红利大小成反向变动2.布莱克-斯科尔斯期权定价模型的假设不包括()。
A.在期权寿命期内,买方期权标的股票不发放股利,也不做其他分配B.任何证券购买者能以短期的无风险利率借得任何数量的资金C.看涨期权可以在到期日之前执行D.所有证券交易都是连续发生的,股票价格随机游走3.下列属于股票加空头看涨期权组合的是()。
A.抛补看涨期权B.保护性看跌期权C.多头对敲D.空头对敲4.假设影响期权价值的其他因素不变,则()。
A.股票价格上升时以该股票为标的资产的欧式看跌期权价值下降B.股票价格下降时以该股票为标的资产的美式看跌期权价值下降C.股票价格上升时以该股票为标的资产的美式看跌期权价值上升D.股票价格下降时以该股票为标的资产的欧式看跌期权价值下降5.下列有关表述中正确的是()。
A.空头期权的特点是最小的净收入为零,不会发生进一步的损失B.期权的到期日价值,是指到期时执行期权可以取得的净收入,它依赖于标的股票在到期日的价格和执行价格C.看跌期权的到期日价值,随标的资产价值下降而下降D.如果在到期日股票价格低于执行价格则看跌期权没有价值6.对于买入看跌期权来说,投资净损益的特点是()。
A.净损失不确定B.净损失最大值为期权价格C.净收益最大值为执行价格D.净收益潜力巨大7.下列表述中不正确的是()。
A.一份期权处于虚值状态,仍然可以按正的价格售出B.如果其他因素不变,随着股票价格的上升,期权的价值也增加C.期权的价值并不依赖股票价格的期望值,而是依赖于股票价格的变动性,如果一种股票的价格变动性很小,其期权也值不了多少钱D. 美式期权的价值应当至少等于相应欧式期权的价值,在某种情况下比欧式期权的价值更大8.某股票的现行价格为100元,看涨期权的执行价格为95元,期权价格为5元,则该期权的时间溢价为()元。

第九章界面现象-习题与解答一.填空1.下,把一半径的水珠分散成的小水珠,则小水滴的数目为()个。
此过程系统=()J。
(已知20℃时,2.同中液体,在一定温度下形成液滴,气泡和平面液体,对应的饱和蒸气压分别为,和,若将三者按大小顺序排列应为()。
3.将一玻璃毛细管垂直插入某液体中,若该液体对毛细管不润湿,则管内液面呈(),产生的附加压力的方向指向(),管内液面管外()平液面。
4.在溶剂中加入某溶质B,能使该溶液的表面张力增大,则该溶质的表面浓度()体相浓度,发生(),该溶质为表面()物质。
5.液体的液滴愈小,饱和蒸气压愈();液体中的气泡愈小,气泡内的液体饱和蒸气压愈()。
6.兰格缪尔单分子层吸附理论的基本假设是()、()、()、()。
7.由于界面效应引起的亚稳定状态有()、()、()、()。
8.物理吸附和化学吸附的本质区别是()。
答案:1. 2. 3.凸形;液体;低于4.低于;负吸附;惰性 5. 愈大;愈小 6.①固体表面是均匀的②吸附是单分子层的;③相邻吸附质分子间无作用力;④吸附与解吸达动态平衡;7.过冷液体;过热液体;过饱和蒸气;过饱和溶液8.吸附剂与吸附质之间作用力不同二.选择题1.下面关于的物理意义中不正确的是()A.σ是沿着与表面相切的方向,垂直作用于表面上单位长度线段上的紧缩力。
B.σ是恒温,恒压下可以可逆的增加单元表面积所需的非体积功。
C.σ是在一定的温度,压力下,单位表面积中的分子所具有G i b b s函数值。
D.σ是恒温,恒压下增加单位表面所引起的系统G i b b s函数值。
2.在吸附过程中,以下热力学量的变化正确的是()A. B.C. D.3.某溶液中溶质B的浓度为(表面)(体相),证明()A. B.C. D.4.溶液的表面层对溶质发生吸附,当表面浓度<本体浓度,则()A.称为正吸附,与纯溶剂相比,溶液的表面张力σ降低。
B.称为无吸附,与纯溶剂相比,溶液的表面张力σ不变。

第九章收入与分配管理一、单选题1.下列各项中,能够反映投资与收入对等原则的是()。
A.企业的收入分配应依法进行B.企业的收入分配必须兼顾各方面的利益C.谁投资谁受益、收入大小与投资比例相对等D.企业的收入分配应坚持积累与分配并重2.可以避免股东双重税收负担,但不能带来税收利益的筹资方式是()。
A.普通股筹资B.内部筹资C.发行债券筹资D.银行借款筹资3.下列销售预测方法中,不属于定性分析方法的是()。
A.营销员判断法B.专家判断法C.趋势预测分析法D.产品寿命周期分析法4.甲公司2014~2017年的销售额分别为:3500万元、3420万元、3800万元和4160万元。
若采用算术平均法,则预测的2018年销售额为()万元。
A.3460B.3720C.3980D.38305.分析影响产品销售量的相关因素以及它们之间的函数关系,并利用这种函数关系进行产品销售预测的方法是()。
A.因果预测分析法B.指数平滑法C.移动平均法D.产品寿命周期分析法6.A公司只生产销售甲产品,该产品的单位完全成本为8.4元,单位变动成本为5.6元。
若本月产量为2500件,则该产品的固定成本总额为()元。
A.7000B.8650C.9150D.48607.若企业设定的定价目标是保持或提高市场占有率,则()。
A.通常为产品制定一个较高的价格B.其产品价格往往需要低于同类产品价格C.跟随行业中的领导企业所制定的价格,与之保持一定的比例关系D.参照对市场有决定性影响的竞争对手的产品价格变动情况,随时调整本企业产品价格8.超市中的美素奶粉标明“原价180元,现促销价149元”,这种策略是()。
A.心理定价策略B.折让定价策略C.组合定价策略D.寿命周期定价策略9.A公司生产销售甲产品,基期销售价格为1500元时,基期销售数量为5000件,当销售价格为2000元时,销售数量为4000件,则该产品的需求价格弹性系数为()。
A.0.6B.0.5C.-0.6D.-0.5110.某汽车会所为了提高市场份额、增强竞争力,特推出了保养送洗车的活动,吸引了大量的有车一族。

第九章企业价值评估一、单项选择题1.下列关于价值评估的目的说法不正确的是()。
A.价值评估的目的是帮助投资人和管理当局改善决策B.企业价值评估提供的结论有很强的时效性C.企业价值评估提供的信息仅仅是企业价值的一个数字D.价值评估认为市场只在一定程度上有效,即并非完全有效2.下列表述不正确的是()。
A.经济价值是指一项资产的公平市场价值,通常用该资产所产生的未来现金流量的现值来计量B.现时市场价格表现了价格被市场所接受,因此与公平市场价值基本一致C.价值评估提供的结论有很强的时效性D.价值评估的一般对象是企业整体的经济价值3.有关企业实体现金流量表述不正确的是()。
A.如果企业没有债务,企业实体现金流量就是可以提供给股东的现金流量B.企业实体现金流量是企业全部现金流入扣除成本费用的剩余部分C.企业实体现金流量是一定期间可以提供给股东和债权人的税后现金流量D.实体现金流量等于股权现金流量加债务现金流量4.甲公司2015年销售收入为10000万元,2015年年底净负债及股东权益总计为5000万元(其中股东权益4400万元),预计2016年销售增长率为8%,税后经营净利率为10%,净经营资产周转率保持与2015年一致,净负债的税后利息率为4%,净负债利息按上年年末净负债余额和净负债税后利息率计算。
下列有关2016年的各项预计结果中,错误的是()。
A.净经营资产净投资为400万元B.税后经营净利润为1080万元C.实体现金流量为680万元D.净利润为1000万元5.下列关系式不正确的是()。
A.实体现金流量=营业现金净流量-(经营长期资产净值增加-经营长期负债增加)B.实体现金流量=税后经营净利润-净经营资产净投资C.债务现金流量=税后利息-净负债增加D.净经营资产净投资=净负债的增加额+所有者权益的增加额6.某公司2014年年末流动负债为300万元,其中金融流动负债为200万元,长期负债为500万元,其中金融长期负债300万元,股东权益为600万元;2015年年末流动负债为550万元,其中金融流动负债为400 万元,长期负债为700万元,其中金融长期负债580万元,股东权益为900万元。

第九章收益分配【学习目的与要求】企业经营如取得收益要制定一个合理的收益分配政策。
本章主要阐述了收益分配政策及股利分配的具体程序。
通过本章学习,应掌握收益分配顺序;收益分配的四种政策;股票股利及股票分割。
【本章重点与难点】本章重点有:收益分配顺序;剩余股利政策、低正常股利加额外股利政策;股票股利。
本章难点有:剩余股利政策;股票股利、股票分割。
一、单项选择题1.( )会导致会计所得与纳税所得的时间性差异。
A.罚息B.多计提的折旧C.滞纳金D.罚金2.公司为了稀释流通在外的本公司股票价格,对股东支付股利的形式应选用()。
A.负债股利B.财产股利C.股票股利D.现金股利3.法定盈余公积转增资本金之后,其余额不得低于注册资本的( )。
A.25% B.15%C.10% D.50%4.下列各项股利分配利政策中,能保持股利与利润间的一定比例关系,体现风险投资与风险收益对等关系的是()。
A.剩余政策B.固定股利政策C.固定股利支付率政策D.低正常股利加额外股利政策5.剩余股利政策的根本目的是()。
A.调整资金结构B.增加留存收益C.更多地使用自有资金进行投资D.降低综合资金成本6.在通货膨胀时期,企业一般采取的收益分配政策是()。
A.没有变化B.比较宽松C.往往偏紧D.时松时紧7.下列收益分配政策中,股利分配方案的股利额与收益之间的关系上固定的是()。
A.固定股利政策B.剩余政策C.固定股利比例政策D.正常股利加额外股利政策8.公司以股票形式发放股利,可能带来的结果是()。
A.引起公司资产的减少B.引起股东权益内部结构变化C.引起公司负债的减少D.引起股东权益与负债同时变化9.下列哪个项目不能用于分派股利( )。
A.上年末分配利润B.资本公积C.税后利润D.盈余公积10.下列哪个项目不能用来弥补亏损( )。
A.盈余公积B.税后利润C.资本公积D.税前利润11.某公司原发行普通股60万股,拟发放5万股股票股利。
已知原每股盈余为4.4元,发放股票股利后的每股盈余将为()。

第九章资本结构一、单项选择题1.下列各种资本结构的理论中,认为筹资决策无关紧要的是()。
A.代理理论B.无税MM理论C.优序融资理论D.权衡理论2.根据有税MM理论,当债务比重增加时,下列各项指标不会发生变化的是()。
A.股权资本成本B.加权平均资本成本C.债务资本成本D.企业价值3.根据无税MM理论,当债务比重增加时,下列各项指标会提高的是()。
A.债务资本成本B.权益资本成本C.加权平均资本成本D.企业价值4.甲公司目前存在融资需求,如果采用优序融资理论,管理层应当选择的融资顺序是()。
A.内部留存收益、发行附认股权证债券、发行公司债券、发行优先股、发行普通股B.内部留存收益、发行附认股权证债券、发行优先股、发行公司债券、发行普通股C.内部留存收益、发行公司债券、发行优先股、发行附认股权证债券、发行普通股D.内部留存收益、发行公司债券、发行附认股权证债券、发行优先股、发行普通股5.下列各项中属于过度投资问题的是()。
A.企业面临财务困境时,企业超过自身资金能力投资项目,导致资金匮乏B.企业面临财务困境时,管理者和股东有动机投资于净现值为负的高风险项目C.企业面临财务困境时,不选择净现值为正的新项目投资D.企业面临财务困境时,管理者和股东有动机投资于净现值为正的项目6.下列关于财务困境成本的相关说法中,错误的是()。
A.发生财务困境的可能性与企业收益现金流的波动程度有关B.财务困境成本的大小取决于成本来源的相对重要性以及行业特征C.财务困境成本的现值是由发生财务困境的可能性和财务困境成本的大小决定的D.不动产密集性高的企业财务困境成本可能较高7.以下关于资本结构的影响因素的说法中,错误的是()。
A.成长性好的企业负债水平高B.盈利能力强的企业负债水平低C.财务灵活性大的企业负债水平高D.一般性用途资产比例高的企业比特殊用途资产比例低的企业负债水平低8.下列各项资本结构决策的分析方法中考虑了财务风险差异的是()。

习题课二重积分的计算一、主要内容二重积分的计算方法是累次积分法,化二重积分为累次积分的步骤是:①作出积分区域的草图②选择适当的坐标系③选定积分次序,定出积分限1。
关于坐标系的选择这要从积分区域的形状和被积函数的特点两个方面来考虑看图定限 —穿越法定限 和不等式定限先选序,后定限①直角坐标系ⅰ。
先 y 后 x ,过任一x ∈ [ a , b ],作平行于 y 轴的直线穿过D 的内部从D 的下边界曲线)(1x y ϕ=穿入—内层积分的下限从上边界曲线)(2x y ϕ=穿出—内层积分的上限ⅱ。
先 x 后 yy 过任一 yy ∈[ c , d ] 作平行于 x 轴的直线定限左边界)(1y x ψ=——内层积分的下限右边界)(2y x ψ=——内层积分的上限则将D 分成若干个简单区域再按上述方法确定每一部分的上下限分片计算,结果相加②极坐标系积分次序一般是θ后先r 过极点O 作任一极角 为 θ]),[(βαθ∈的射线从D 的边界曲线 )(1θr 穿入从 )(2θr 穿出ⅲ。
如D 须分片)(1θr ——内下限)(2θr —内上限具体可分为三种情况)()(,21θθβθαr r r ≤≤≤≤⑵极点在D 的边界上)()(,21θθβθαr r r ≤≤≤≤是边界在极点处的切线的极角βα,)(1θr 绝大多数情况下为0⑶极点在D 的内部)(0,20θπθr r ≤≤≤≤化累次积分后外限是常数内限是外层积分变量的函数或常数极坐标系下勿忘 r⑴极点在D 的外部∫∫∫∫=D Ddxdy x y f dxdy y x f ),(),(——称为关于积分变量的轮换对称性是多元积分所独有的性质奇函数关于对称域的积分等于0,偶函数关于对称域的积分等于对称的部分区域上积分的两倍,完全类似于 对称区间上奇偶函数的定积分的性质简述为“你对称,我奇偶”①、②、③简单地说就是④若 DD 关于直线 y = x 对称。

第九章产品成本计算与分析一、单项选择题1、下列企业中,不适用分步法的是()。
A.冶金B.纺织C.机械制造D.发电2、甲公司是一家从事矿石采掘的企业,则其适宜采用的成本计算方法是()。
A.分批法B.定额法C.品种法D.分类法3、下列关于逐步结转分步法的表述中,不正确的是()。
A.能够提供各个生产步骤的半成品成本资料B.为各生产步骤的在产品实物管理及资金管理提供资料C.能够全面地反映各生产步骤的资产耗费水平D.不必逐步结转半成品成本4、甲公司生产N产品,材料消耗量12月份计划100千克,实际耗用120千克;材料的价格计划1 0元/千克,本月实际10.5元/千克。
甲公司12月份材料消耗量变动的影响是()元。
A.50B.60C.200D.2105、甲公司实现计时工资制度生产M产品,M产品每台所耗工时数计划为320小时,实际为300小时;每小时工资成本计划为12元/小时,实际为13元/小时。
甲公司因每小时工资成本变动对产品成本的影响为()元。
A.240B.300C.320D.3606、通过计算成本利润率对企业经营效益进行评价的方法属于()。
A.对比分析法B.构成比率分析法C.相关指标比率分析法D.趋势分析法7、下列各项对产品成本的分析方法中,属于构成比率分析的是()。
A.将本期实际成本与前期实际成本进行比较B.计算分析本期的成本利润率C.计算制造费用占产品成本的比重D.计算分析本期销售收入成本率8、A企业甲产品的单位成本为2 000元,其中,直接材料1 160元,直接人工440元,制造费用400元。
则甲产品的直接材料成本比率为()。
A.60%B.58%C.50%D.33%9、可比产品单位成本下降对可比产品成本降低指标的影响是()。
A.可比产品成本降低额增加,可比产品成本降低率提高B.可比产品成本降低额减少,可比产品成本降低率不变C.可比产品成本降低额增加,可比产品成本降低率减少D.可比产品成本降低额减少,可比产品成本降低率提高10、某企业生产甲产品,属于可比产品,上年实际平均单位成本为100元,上年实际产量为1 800件,本年实际产量为2 000件,本年实际平均单位成本为98元,则本年甲产品可比产品成本降低率为()元。
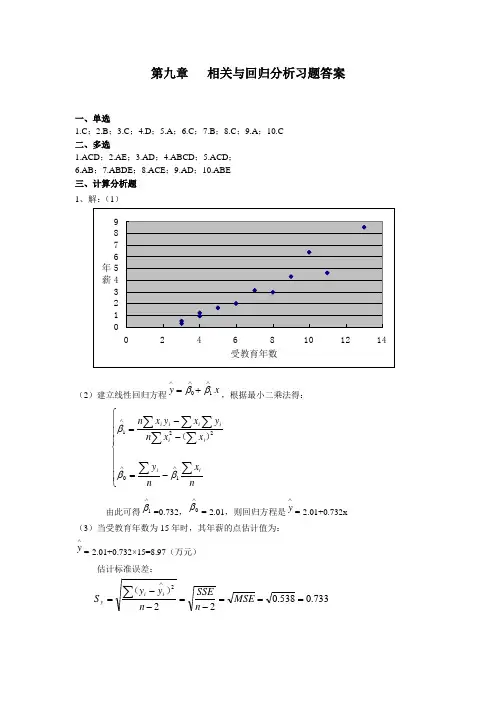
第九章 相关与回归分析习题答案一、单选1.C ;2.B ;3.C ;4.D ;5.A ;6.C ;7.B ;8.C ;9.A ;10.C 二、多选1.ACD ;2.AE ;3.AD ;4.ABCD ;5.ACD ;6.AB ;7.ABDE ;8.ACE ;9.AD ;10.ABE 三、计算分析题 1、解:(1)(2)建立线性回归方程xy ∧∧∧+=10ββ,根据最小二乘法得:⎪⎪⎪⎩⎪⎪⎪⎨⎧-=--=∑∑∑∑∑∑∑∧∧∧n x n y x x n y x y x n i i i i i i i i 10221βββ)(由此可得∧1β=0.732,∧0β=-2.01,则回归方程是∧y =-2.01+0.732x(3)当受教育年数为15年时,其年薪的点估计值为:∧y =-2.01+0.732×15=8.97(万元)估计标准误差: 733.0538.0222===-=--=∑∧M S E n S S En y y S i iy )(置信区间为:∑=∧--+±n i i yx x x x nS t y 1202/)()(12α=8.97±2.228×0.733×9167.120917.6151212)(-+=8.97±1.290预测区间为:∑=∧--++±ni i yx x x x nS t y 1202/)()(112α=8.97±2.228×0.733×9167.120917.61512112)(-++ =8.97±2.081 2、解:(1)建立线性回归方程xy ∧∧∧+=10ββ,根据最小二乘法得:⎪⎪⎪⎩⎪⎪⎪⎨⎧-=--=∑∑∑∑∑∑∑∧∧∧n x n y x x n y x y x n i i i i i i i i 10221βββ)(由此可得0093.00=∧β,316.01=∧β,则回归方程是x y 316.00093.0+=∧(3)当GDP 达到16时,其货币供应量的点估计值为:∧y =0.0093+0.316×16=5.065亿元估计标准误差:Sy=22--∑∧n y y i i)(=2-n SSE=MSE =09294.0=0.305置信区间为:∑=∧--+±n i i yx x x x nS t y 1202/)()(12α=5.065±2.228×0.305×21863.135711.11161212)(-+ 3、(1)利用EXCEL 的CORREL 函数计算相关系数r=0.9937.相关系数接近于1,表明农业总产值与农村购买力之间有较强的正线性相关关系。

第九章财务分析习题及答案一、单项选择题1. 某企业现在的流动比率为2 :1 ,下列哪项经济业务会引起该比率降低()。
A.用银行存款偿还应付账款B.发行股票收到银行存款C. 收回应收账款D.开出短期票据借款D2.如果流动比率大于1,则下列结论成立的是()。
A.速动比率大于1B.现金比率大于1C. 营运资金大于0D.短期偿债能力绝对有保障C3.在企业速动比率是0.8的情况下,会引起该比率提高的经济业务是()。
A.银行提取现金B.赊购商品C. 收回应收账款D.开出短期票据借款D4.某企业年初流动比率为2.2,速动比率为1;年末流动比率为2.4,速动比率为0.9。
发生这种情况的原因可能是()。
A.当存货增加B.应收账款增加C. 应付账款增加D.预收账款增加.A5.如果流动资产大于流动负债,则月末用现金偿还一笔应付账款会使()。
A.营运资金减少B.营运资金增加C. 流动比率提高D.流动比率降低C6.影响企业短期偿债能力的最根本的原因是()。
A.企业的资产结构 B.企业的融资能力C.企业的权益结构 D.企业的经营业绩D7.运用资产负债表可计算的比率有()。
A.应收账款周转率 B.总资产报酬率C.利息保障倍数 D.现金比率D8.总资产报酬率是指()与平均总资产之间的比率。
A.利润总额B.息税前利润C.净利润D.息前利润B9.()是反映盈利能力的核心指标。
A.总资产报酬率B.股利发放率C.总资产周转率D.净资产收益率D10.()指标越高,说明企业资产的运用效率越好,也意味着企业的资产盈利能力越强。
A.总资产周转率B.存货周转率C.总资产报酬率D.应收账款周转率C11. 如果企业速动比率很小,下列结论成立的是()。
A 企业流动资产占用过多B 企业短期偿债能力很强C 企业短期偿债风险很大D 企业资产流动性很强C12.在企业各收入利润率中,()通常是其他利润率的基础。
A.产品销售利润率B.营业收入利润率C.总收入利润率D.销售净利润率A13. 不影响净资产收益率的指标包括()。

第九章同步试题及解析-、单项选择题1.下列关于公司净利润分配的说法中,正确的是()。
A.公司从税后利润中提取法定公积金后,经董事会批准,还可以从税后利润中提取任意公积金B.公司向投资者(股东)分配股利(利润)时,股份有限公司股东按照实缴出资比例分红C.法定公积金可用于弥补亏损或转增资本D.税后利润弥补亏损必须用当年实现的净利润5.以下不属于股票回购对上市公司的影响的是()。
A.可以有效地防止敌意收购B.容易造成资金紧张,降低资产流动性,影响公司后续发展C.容易导致公司操纵股价D.忽视了公司的长远发展,损害了公司的根本利益7.股票分割又称拆股,即将-股股票拆分成多股股票,下列关于股票分割的说法中,不正确的是()。
A.不影响公司的资本结构B.不改变股东权益的总额C.会改变股东权益内部结构D.会增加发行在外的股票总数8.下列关于股票分割和股票股利的共同点的说法中,不正确的是()。
A.均可以促进股票的流通和交易B.均有助于提高投资者对公司的信心C.均会改变股东权益内部结构D.均对防止公司被恶意收购有重要的意义9.为了提高销售收入,保障企业利润,并且可以有效打击竞争对手,应采取的定价目标为()。
A.保持或提高市场占有率B.树立企业形象及产品品牌C.应付和避免竞争D.规避风险10.盈利水平随着经济周期而波动较大的公司或行业适用的股利分配政策是()^ A.剩余股利政策B.固定股利政策C.固定股利支付率政策D.低正常股利加额外股利政策11.某公司目前的普通股2000万股(每股面值1元),资本公积1000万元,留存收益1200万元。
发放10%的股票股利后,股本增加()万元。
A.200B.1200C.240D.30013.下列不属于确定利润分配政策应考虑的公司因素是()。
A.资产的流动性B.现金流量C.投资机会D.超额累积利润约束14.下列关于股利支付形式的说法中,不正确的是()。
A.财产股利和负债股利实际上是现金股利的替代B.股票股利会引起所有者权益内部结构发生变化C.以公司所拥有的其他公司的债券支付股利,属于支付负债股利D.发放股票股利可能导致资本公积增加15.某公司2010年的税后利润为2000万元,年末的普通股股数为1000万股,2011年的投资计划需要资金2200万元,公司的目标资本结构为权益资本占60%,债务资本占40%。
第九章 统计指数(一)单选题1、如果销售额增加10%,零售物价指数下降5%,则销售量( )A 、增加5%B 、增加10%C 、增加15.79%D 、无法判断2、综合指数是依据以下方式来编制的A 、先对比,后平均B 、先综合,后对比C 、先除后乘D 、先加后除3、平均指数是依据以下方式来编制的A 、先对比,后平均B 、先综合,后对比C 、先除后乘D 、先加后除4、通常在指数体系的完整框架中,质量指标指数是以( )计算的。
A 、拉氏公式B 、帕氏公式C 、马-埃公式D 、费雪公式5、通常在指数体系的完整框架中,数量指标指数是以( )计算的。
A 、拉氏公式B 、帕氏公式C 、马-埃公式D 、费雪公式6、某商店销售多种商品,报告期与基期相比销售额未变,但销售量增长了15%,则销售价格指数为( )A 、115%B 、100%C 、85%D 、86.96%7、编制平均指数的基本问题之一是( )A 、指数化指标的选择问题B 、合理加权问题C 、同度量因素的固定问题 D 、以上答案均错8、用于比较不同地区或国家各种商品价格综合差异程度的指数是( )A 、个体价格指数B 、时间价格指数C 、空间价格指数D 、平均价格指数9、我国的消费者价格指数(CPI )是采用( )来编制的。
A 、固定加权算术平均的形式B 、固定加权调和平均的形式C 、固定加权几何平均的形式 D 、简单算术平均的形式10、采用标准比值法编制综合评价指数时,个体指数的计算方法为( )A 、参评指标标准值比相应指标报告期值B 、参评指标报告期值比相应指标基期值C 、参评指标计划值比相应指标标准值D 、参评指标实际值比相应指标标准值11、P 表示商品价格,q 表示商品销售量,则∑-∑1011q p q p 的意义是综合反映多种商品的( )A 、销售量变动的绝对额B 、价格变动的绝对额C 、因价格变动额增减的销售额D 、因销售量变动额增减的销售额12、以个体指数为基础计算总指数的指数形式是( )A 、综合指数B 、平均指数C 、可变构成指数D 、固定构成指数13、某商品价格发生变化,现在的100元只值原来的90元,则价格指数为( )A 、10.00%B 、90.00%C 、110.00%D 、111.11%14、某企业职工工资总额,今年比去年减少2%,而平均工资上升5%,则职工人数减少( )A 、3.0%B 、10.0%C 、75.0%D 、6.7%二、多项选择题1、以下属于时间指数的是( )A 、股票价格指数B 、计划完成情况指数C 、零售物价指数D 、地区间的价格比较指数 E 、工业生产指数2、以下属于质量指标指数的是( )A 、股价指数B 、物价指数C 、成本指数D 、产量指数E 、销售量指数3、以下属于数量指标指数的是( )A 、工业生产指数B 、商品销售额指数C 、总产值指数D 、产量指数 E 、销售量指数4、个体指数( )A 、是反映个别现象或个别项目数量变动的指数B 、采用先综合、后对比的方式编制 C 、采用先对比、后综合的方式编制 D 、也有质量指标指数和数量指标指数之分 E 、是总指数的重要形式之一5、同度量因素的作用有( )A 、“同度量”的作用B 、“平衡”的作用C 、对指数化指标“加权”的作用 D 、“平均”的作用 E 、以上均对6、某商店报告期全部商品的销售量指数为120%,这个指数是( )A 、个体指数B 、总指数C 、数量指标指数D 、质量指标指数 E 、平均数指数7、可变构成指数的意义及公式( )A 、可变构成指数反映了各组的变量水平及总体结构两个因素的影响B 、可变构成指数仅反映总体结构的影响C 、可变构成指数的计算公式为:D 、可变构成指数的计算公式为:E 、可变构成指数的计算公式为: 8、固定构成指数的意义及公式( )A 、固定构成指数反映了各组的变量水平的影响B 、固定构成指数反映了总体结构的影响C 、固定构成指数的计算公式为:∑∑÷∑∑=0001100f f x f f x x x 假定∑∑÷∑∑=00011101f f x f f x x x ∑∑÷∑∑=1101111f f x f f x x x 假定∑∑÷∑∑=0001100f f x f f x x x 假定∑÷∑=00111f x f x xD 、固定构成指数的计算公式为:e 、固定构成指数的计算公式为: 9、结构影响指数的意义及公式( )A 、结构影响指数反映了各组的变量水平的影响B 、结构影响指数反映了总体结构的影响C 、结构影响指数的计算公式为:D 、结构影响指数的计算公式为:E 、结构影响指数的计算公式为: 10、加权总指数的编制方式有( )A 、先综合、后对比B 、先加后减C 、先减后加 D 、先对比、后平均 E 、先除后乘11、总指数的计算形式有( )A 、综合指数B 、销售量指数C 、销售价格指数D 、平均指数E 、产量指数三、填空题1、在我国,工业生产指数是通过计算各种工业产品的 产值来加以编制的。
第九章产品成本计算与分析(课后作业)一、单项选择题1.在大量大批且为单步骤生产的情况下,产品成本的计算方法一般是()。
A.品种法B.分步法C.逐步结转分批法D.平行结转分步法2.企业在进行成本计算方法选择时,对于所试制的新产品应采用()。
A.品种法B.分批法C.分步法D.分类法3.产品成本计算不定期,一般也不存在完工产品与在产品之间费用分配问题的成本计算方法是()。
A.平行结转分步法B.逐步结转分步法C.分批法D.品种法4.在计算产品成本时,不计算各步骤所产半成品成本,也不计算各步骤所耗上一步骤的半成品成本,只计算本步骤发生的各项其他成本,以及这些成本中应计入产成品的份额,这种方法属于()。
A.平行结转分步法B.逐步结转分步法C.综合结转法D.分项结转法5.某企业生产W产品,属于可比产品,上年实际平均单位成本为125元,上年实际产量为990件,本年实际产量为1100件,本年实际平均单位成本123.35元,则本年W产品可比产品成本降低率为()。
A.0.156.某企业生产甲产品,属于可比产品,上年实际平均单位成本为75元,上年实际产量为2200件,本年实际产量为2100件,本年实际平均单位成本为73.5元,则本年甲产品可比产品成本降低额为()元。
A.1000B.2000C.3150D. 60007.某企业2011年成本为657万元,销售收入为1020万元。
则该企业的营业收入成本率为()。
A. 40%B. 60%C.64.41%D. 155.25%8.某企业A产品的单位成本为158元,其中,原材料101元,直接人工32元,制造费用25元。
则W产品中直接材料的成本比率为()。
A.20.25%B.60%C.63.92%D.15.82%9.某企业本月生产甲产品750件,实际使用材料1250千克,材料实际采购价格180元/千克;直接材料的计划价格175元/千克,计划材料消耗量为1500千克,则该企业本月材料价格差异为()元。
第九章一、单项选择题1.在进行投资项目评价时,投资者要求的风险报酬取决于该项目的( C )。
A.经营风险B.财务风险C.系统风险D.特有风险2.风险调整折现率法使用的折现率是( A )。
A.风险调整折现率B.无风险报酬率C.借款利息率D.市场平均报酬率3.运用肯定当量法进行投资风险分析,需要调整的项目是( C )。
A.有风险的折现率B.无风险的折现率C.有风险的现金流量D.无风险的现金流量4.可以根据各年不同的风险程度对方案进行评价的方法是( B )。
A.风险调整贴现率法B.肯定当量法C.内含报酬率法D.现值指数法5.在用平均年成本法进行固定资产更新时,残值收入作为( C )来考虑A.现金流入D.现金流入的抵减6.以下是等额年金法和共同年限法共有的缺点是( C )。
A.两种方法均不便于理解B.两种方法预计现金流量的工作都比较难C.从长期来看,竞争会使项目净利润下降,甚至被淘汰,但两种方法均没有考虑D.两种方法的应用都比较复杂7.一个公司“当期的营业性现金净流入量等于当期的净利润加折旧之和”,就意味着( D )。
A.该公司不会发生偿债危机B.该公司当期没有分配股利C.该公司当期的营业收入都是现金收入8.在进行投资项目风险分析时,易夸大远期现金流量风险的方法是( B )。
A.调整现金流量法B.风险调整折现率法C.净现值法D.内含报酬率法9.下列说法中正确的是( A )。
A.以实体现金流量法和股权现金流量法计算的净现值两者无实质区别B.实体现金流量包含财务风险,比股东的现金流量风险大C.如果市场是完善的,增加债务比重会降低平均资本成本D.股权现金流量法比实体现金流量法简洁10.在进行是继续使用旧设备还是购置新设备决策时,如果这两个方案的未来使用年限不同,且只有现金流出,没有适当的现金流入。
则最为合适的评价方法是( D )。
A.比较两个方案总成本的高低B.比较两个方案净现值的大小C.比较两个方案内含报酬率的大小D.比较两个方案平均年成本的高低11.下列说法错误的是( C )。
第九章组合逻辑电路一.填空题:(每空1分)1、 组合逻辑电路任何时刻的输出信号,与该时刻的输入信号 有关 ,与以前的输入信号 无关 。
2、 8线—3线优先编码器74LS148的优先编码顺序是7I 、6I 、5I 、…、0I ,输出为2Y 1Y 0Y 。
输入输出均为低电平有效。
当输入7I 6I 5I …0I 为11010101时,输出2Y 1Y 0Y 为 010 。
3、 3线—8线译码器74HC138处于译码状态时,当输入A 2A 1A 0=001时,输出07Y ~Y =11111101 。
4、 实现将公共数据上的数字信号按要求分配到不同电路中去的电路叫 数据分配器。
5、 根据需要选择一路信号送到公共数据线上的电路叫 数据选择器 。
6、 一位数值比较器,输入信号为两个要比较的一位二进制数,用A 、B 表示,输出信号为比较结果:Y (A >B ) 、Y (A =B )和Y (A <B ),则Y (A >B )的逻辑表达式为 AB 。
7、 能完成两个一位二进制数相加,并考虑到低位进位的器件称为 全加器 。
8、 组合逻辑电路是由____与__门、_或___门、___非___门等几种基本门电路组合而成,任意时刻,它的输出直接由该时刻的_____输入________所决定。
9、 编码器的功能是把输入的信号转化成___二进制代码_______。
10、如图9-3-1所示的逻辑电路,输入0I 有效时,输出01Y Y =__00______;输入1I 有效时,输出01Y Y =_______01___;输入2I 有效时,输出01Y Y =______10___;输入3I 有效时,输出01Y Y =___11______。
该逻辑电路为___二进制_____编码器。
图9-3-111、半导体数码管按内部发光管的接法可分为___共阴极数码管____和__共阳极数码管_________两种。
数码显示器通常有____半导体数码管______、___液晶显示器_________、___荧光显示器 12、_______三种。
第九章收入与分配管理一、单项选择题〔本小题备选答案中,只有一个符合题意的正确答案。
多项选择、错选、不选均不得分。
〕1.以下净利润分配事项中,根据相关法律法规和制度,应当最后进行的是〔〕。
C.提取法定公积金2.以下方法中属于可能受权威专家的影响,客观性较差的方法是〔〕。
3.进行销售预测分析时,趋势预测分析法中在实践中运用较多的产品销售预测方法是〔〕。
4.某企业生产 A 产品,本期方案销售量为 10000 件,应负担的固定本钱总额为 250000 元,单位产品变动本钱为 70 元,适用的消费税税率为 5%,根据上述资料,运用保本点定价法测算的单位 A 产品的价格应为〔〕元。
5.某企业生产 C 产品,本期方案销售量为 5000 件,目标利润总额为 100000 元,完全本钱总额为 256250元,适用的消费税税率为 5%,根据上述资料,运用目标利润法测算的单位产品的价格应为〔〕元。
6.以下关于利润分配的描述中,正确的选项是〔〕。
A.公司在提取法定公积金之前,应领先用当年利润弥补亏损B.法定公积金的提取比例为当年税后利润〔弥补亏损后〕的 20%7.以下股利理论中,认为少发股利较好的是〔〕。
B.“手中鸟〞理论8.某公司 2021 年度净利润为 2000 万元,预计 2021 年投资所需的资金为 4000 万元,假设目标资本结构是负债资金占 60%,企业按照净利润 10%的比例计提法定盈余公积金,公司采用剩余股利政策发放股利,那么2021 年度企业可向投资者支付的股利为〔〕万元。
9.在以下股利政策中,股利与利润之间保持固定比例关系,表达风险投资与风险收益对等关系的是〔〕。
10.最适用于盈利随着经济周期而波动较大的公司的股利政策是〔〕。
11.在确定企业的收益分配政策时,应当考虑相关因素的影响,其中“资本保全约束〞属于〔〕。
12.以下关于股利分配政策的表述中,正确的选项是〔〕。
C.基于控制权的考虑,股东会倾向于较高的股利支付水平13.以下各项股利支付形式中,不会改变企业资本结构的是〔〕。
练习题1.甲股份有限公司(以下简称甲公司)于2008年1月1日从乙租赁公司(以下简称乙公司)租人一台全新设备,用于行政管理。
租赁合同的主要条款如下:
(1)租赁起租日:2008年1月1日。
(2)租赁期限:2008年1月1日至2009年12月31日。
甲公司应在租赁期满后将设备归还
给乙公司。
(3)租金总额:240万元。
(4)租金支付方式:在起租日预付租金160万元,2008年年末支付租金40万元,租赁期满
时支付租金40万元。
起租日该设备在乙公司的账面价值为l 000万元,公允价值为l 000万元。
该设备预计使用年限为10年。
甲公司在2008年1月1日的资产总额为2 400万元。
甲公司对于租赁业务所采用的会计政策是:对于融资租赁,采用实际利率法分摊未确认融资费用;对于经营租赁,采用直线法确认租金费用。
甲公司按期支付租金,并在每年年末确认与租金有关的费用。
乙公司在每年年末确认与租金有关的收入。
同期银行贷款年利率为6%。
假定不考虑在租赁过程中发生的其他相关税费。
要求:(1)判断此项租赁的类型,并简要说明理由。
(2)编制甲公司与租金支付和确认租金费用有关的会计分录。
(3)编制乙公司与租金收取和确认租金收入有关的会计分录。
(答案中金额单位用万元表示)
作业题1.甲公司于2009年12月10日与乙租赁公司签订了一份设备租赁合同。
合同主要条款如下:(1)租赁标的物:A生产设备。
(2)起租日:2009年12月31日。
(3)租赁期:2009年12月31日至2013年12月31日。
(4)租金支付方式:2010年至2013年每年年末支付租金600万元。
(5)租赁期满时,A生产设备的估计余值为400万元,其中甲公司担保的余值为300万元,未担保的余值为100万元。
(6)2009年12月31日,A生产设备在乙公司的账面价值为2 500万元,公允价值也为2 500万元.已使用3年,预计还可使用5年。
(7)租赁合同年利率为6%。
(8)2013年12月31日,甲公司将A生产设备归还给乙租赁公司。
(9)假定甲公司无法获知乙公司的租赁内含利率。
2009年12月31日,A生产设备运抵甲公司,当日投人使用。
甲公司固定资产均采用平均年限法计提折旧。
已知:[(P/A,6%,4)= 3.4651;(P/V,6%,4)= 0.7921;
(P/A.2%,4)= 3.8077;(P/V,2%,4)= 0.9238 ] 要求:
(1)判断该租赁的类型,并说明理由。
(2)编制甲公司在租赁期开始目的有关会计分录。
(3)编制甲公司在2010年年末至2013年年末与租金支付以及其他与租赁事项有关的会计分录(假定相关事项均在年末进行账务处理)。
(4)计算乙公司的租赁内含利率并编制其在2010年的有关会计分录(结果保留两位小数,金额单位用万元表示)。
练习题2.2007年12月1日,甲公司与乙租赁公司签订了一份租赁合同。
主要条款及有关资料如下:(1)租赁标的物:某大型机器生产设备。
(2)租赁期开始日:2007年12月31日。
(3)租赁期;2007年12月31日~2010年12月31日,共计36个月。
(4)租金支付方式:自承租日起每6个月于月末支付租金225 000元。
(5)该设备在租赁开始日的公允价值与账面价值均为1 050 000元。
(6)租赁合同规定年利率为14%。
(7)该设备的估计使用年限为9年,已使用4年,期满无残值,承租人采用年限平均法计提折旧。
(8)租赁期满时,甲公司享有优惠购买选择权.购买价150元。
估计期满时的公允价值
300 000元。
(9)2009年和2010年两年甲公司每年按该设备所生产的产品的年销售收人的5%向乙租赁
公司支付经营分享收人。
甲公司2009年和2010年销售收人为350 000元、400 000—500 000元。
此外,该设备不需安装。
(10)承租人在租赁谈判和签订租赁合同过程中发生的,可归属于租赁项目的手续费、律师
费、差旅费、印花税等初始直接费用共计10 000元,以银行存款支付。
出租人在租赁谈判和签订租赁合同过程中发生的直接费用共计15 000元.以银行存款支付。
[(P/A,7%,6)= 4.7665;(P/F,7%,6)= 0.6663;
225 000 ×(P/A,7.7%,6)+150×(P/F,7.7%,6)= l 050 000 ]
要求:
(1)判断租赁类型。
(2)确定租赁资产入账价值并编制会计分录。
(3)缩制2008年6月30日、12月31日未确认融资费用分摊的会计分录。
(4)编制2008年12月31日按年计提折旧的会计分录。
(5)编制2009年和2010年有关或有租金的会计分录。
(6)编翩2010年12月31日租赁期满时留购租赁资产的会计分录。